基于无矩理论的凹版印刷机运动薄膜横向振动特性及稳定性
2019-01-08武吉梅邵明月雷文姣
武吉梅 邵明月 田 振 雷文姣 王 砚
1.西安理工大学机械与精密仪器工程学院,西安, 710048 2.西安理工大学印刷包装与数字媒体学院,西安, 710048 3.西安理工大学土木建筑工程学院,西安, 710048
0 引言
印刷过程中,中间印刷滚筒对薄膜的约束可视为薄膜的中间支承,不同的支撑位置对薄膜的振动特性有影响,因此,研究具有中间刚性支承运动印刷薄膜的振动问题,对控制印刷过程中薄膜的振动及提高印品的套印精度具有重要的意义。
近年来,轴向运动系统的横向振动和稳定性问题的研究已经取得较大成果,但对具有中间支承的薄膜的振动和稳定性的研究很少。TANG等[1-3]分别对轴向运动的弦线、黏弹性梁、薄板的横向振动问题进行了研究。MA等[4]采用有限差分法离散动力学方程,研究了变密度运动薄膜的振动控制问题。WANG等[5]运用薄板理论和二维黏弹性本构关系,研究了轴向运动的压电黏弹性板的动力学特性和稳定性。SHINA等[6]应用哈密顿原理建立了无滑动边界条件下运动薄膜的微分方程,研究了轴向运动薄膜的面内和面外的动力学特性。吴晓[7]采用解析法研究了无轴向运动速度且具有中间支承的薄膜的横向振动特性。MARYNOWSKI[8]采用二维流变理论,建立了轴向运动的黏弹性薄膜材料的动力学模型。刘金堂等[9]采用微分求积法,研究了受面内载荷作用的轴向运动薄板的横向振动问题。赵凤群等[10]对四边固支矩形运动薄膜的非线性振动特性进行了分析。NGUYEN等[11-12]研究了具有轴向运动速度的薄膜的横向振动特性和控制问题。WU等[13-14]运用振动理论和达朗贝尔原理,分别研究了多辊支承的轴向运动纸带和弹性边界下运动薄膜的振动特性。
本文通过研究,将单刚性支承薄膜拓展到若干刚性支承情况下薄膜的横向振动特性及稳定性问题,分析具有刚性支承时系统的固有振动频率与张力、速度之间的关系曲线,给出薄膜稳定工作的临界速度及工作范围。
1 振动模型的建立
图1为具有中间支承印刷薄膜的工作示意图。对于机组式凹版印刷机,I1、I2、I3为压印滚筒,P1、P2、P3为印版滚筒。高速运动的薄膜从几组滚筒之间的接触表面通过,完成多色套印印刷。印刷过程中,运动的薄膜类承印物遵循薄膜振动理论,将中间印刷滚筒对薄膜的作用作为薄膜的中间支承处理,并用线分布的约束反力代替,将印刷机第一色组和最后色组的印刷滚筒对薄膜的作用作为边界条件处理,建立薄膜的动力学模型。

图1 印刷薄膜工作简图和受力简图Fig.1 Schematic diagram of an axially moving membrane
如图1所示,选取OXYZ坐标系:以薄膜的运动方向为X方向,该方向的运动速度为v;薄膜的宽度方向为Y方向;横向振动的位移方向为Z方向。a、b分别为两组印刷滚筒间薄膜的长度和宽度;ρ为单位面积薄膜的质量;Tx为薄膜在X方向上受到单位长度的拉力,N/m;Ty为薄膜在Y方向上受到单位长度的拉力,N/m。
基于无矩理论[15]和D’Alembert原理得出轴向运动印刷薄膜横向振动偏微分方程:
q(x,y,t)
(1)

四边固支薄膜的边界条件为

(2)
2 特征方程的求解
设式(1)的解为

(3)
式中,U(x)是振型函数;ω为运动薄膜的振动频率。
具有中间支承的印刷薄膜固有振动时,中间支承的约束反力随时间的变化规律与印刷薄膜的振动规律相同。式(1)的分布载荷q(x,y,t)为薄膜沿Z方向所受均布外力,可表示为
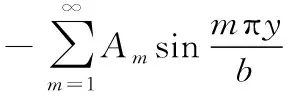
(4)
(5)
式中,N为中间支承的个数;xi为第i个支承到Y轴距离;pi为第i个支承对薄膜的支承反力;δ(x-xi)为Dirac-delta函数,表示作用在(xi,y)位置上的支承反力。
设振型函数为
(6)
由四边固支的边界条件有
fm(0)=fm(a)=0m=1,2,…
(7)
将式(3)、式(4)、式(6)代入式(1)并整理得
(8)
(9)
对式(8)进行Laplace变换得
(10)

对式(10)进行Laplace逆变换,并代入式(7)可得
sin(λ(x-xi))g(x-xi)
(11)
将式(11)代入式(6),然后再代入式(3),得到具有中间支承四边固支运动印刷薄膜的固有振动动力响应:
(12)

(13)
(14)
i,j=1,2,…,N
当薄膜中间支承为弹性支承时,pj=-kjfm(xj),其中,kj为第j个弹性支承的刚度系数。由式(11)得到具有中间支承的运动薄膜的振动频率特征方程:
(15)
3 数值计算分析
本文以陕西北人FR-300无轴传动高速机组式凹版印刷机的承印物薄膜为实例,计算分析具有中间刚性支承的运动印刷薄膜的横向振动特性及稳定性。该印刷机的基本参数如下:薄膜幅宽b=1.05 m,薄膜长度a=3 m,薄膜速度v=5 m/s,薄膜张力Tx=90 N/m,Ty=10 N/m,密度ρ=0.07 kg/m2。
3.1 具有一个中间刚性支承
图2所示为一个中间刚性支承的印刷薄膜,中间支承的位置与左端的距离为a/h,由式(13)可得中间具有一个刚性支承运动印刷薄膜的振动频率特征方程:
(16)

图2 中间一个刚性支承Fig.2 Single intermediate rigid support
由式(16)可得
(17)
由文献[7]可知,没有中间支承时的四边固支薄膜横向振动频率特征方程为
sin(λa)=0
(18)
h=2时,式(17)化为
(19)
具有一个刚性支承运动薄膜的中间支撑位置为x=1.5 m,则运动薄膜的振动圆频率为
(20)
v=0时,无轴向速度薄膜的振动圆频率为
(21)
v=0时的振动圆频率表达式与文献[7]中的中间一个刚性支承的薄膜振动圆频率表达式一致,由此说明本文所用方法的正确性。
由式(20)、式(21)可求出v=5 m/s及v=0时的运动薄膜振动圆频率,分别用ωv=5和ωv=0表示,如表1所示。

表1 具有一个中间刚性支承薄膜的振动圆频率
由表1可知,v=5 m/s及v=0时的薄膜振动圆频率不同,因此,轴向运动速度对印刷薄膜横向振动影响显著。由式(20)可得印刷薄膜固有振动圆频率ω与轴向运动速度v之间的关系曲线,如图3所示。

图3 薄膜振动复频率与轴向运动速度的关系Fig.3 Relationship between complex frequency and axial moving speed
由图3可以看出,速度0~35.86 m/s内,薄膜复频率ω11逐渐降低至0;在速度范围35.86~39.72 m/s内,Re(ω)=0,此时Im(ω)出现,印刷薄膜系统发散失稳。当v>39.72 m/s时,印刷薄膜系统恢复稳定。对于薄膜复频率ω12,速度在35.86~36.86 m/s内时,Re(ω)=0,印刷薄膜系统发散失稳;当v>36.86 m/s时,印刷薄膜系统恢复稳定。
图4所示为单刚性支撑薄膜轴向速度v=5 m/s时ω与Tx的关系。由图4可知,随着Tx的增大,ω逐渐增大。当v=5 m/s时,在0≤Tx<1.75 N/m内,Re(ω)=0,虚部突然增大,印刷薄膜系统处于发散失稳状态;当Tx>1.75 N/m时,虚部为零,印刷薄膜系统恢复稳定。

图4 薄膜复频率与X向张力关系(v=5 m/s)Fig.4 Relationship between the complex frequency and tension(v=5 m/s)
3.2 中间具有两个刚性支承
图5为中间具有两个刚性支承的运动印刷薄膜示意图。最左端与第一个刚性支承位置的距离x1=a/3,即x1=1 m。最左端与第二个刚性支承位置的距离x2=2a/3,即x2=2 m。

图5 中间具有两个刚性支承的运动印刷薄膜Fig.5 Moving membrane with two intermediate rigid supports
由式(13)可求得中间具有两个刚性支承运动印刷薄膜振动频率特征方程:
A11A22-A21A12=0
(22)
具有2个中间刚性支承印刷薄膜可以看成三段长度均为a/3且无中间支承运动印刷薄膜。则其中一段印刷薄膜固有振动频率特征方程为
(23)
那么具有两个中间刚性支撑运动印刷薄膜的振动圆频率为
v=0时,式(24)退化为无轴向速度且具有两个中间刚性支承的运动印刷薄膜的振动圆频率:
(25)
退化后的振动圆频率表达式与文献[7]中的中间两个刚性支承的薄膜固有振动圆频率表达式一致,由此说明本文所用方法的正确性。
由以上分析可类推出具有N个均匀分布刚性支承运动印刷薄膜固有振动圆频率:
(26)
v=0时,式(26)退化为无轴向速度的具有N个均匀分布刚性支承薄膜的振动圆频率:
(27)
由式(24)可求得具有两个中间刚性支承运动印刷薄膜的振动圆频率ω与轴向运动速度v之间的关系,如图6所示。
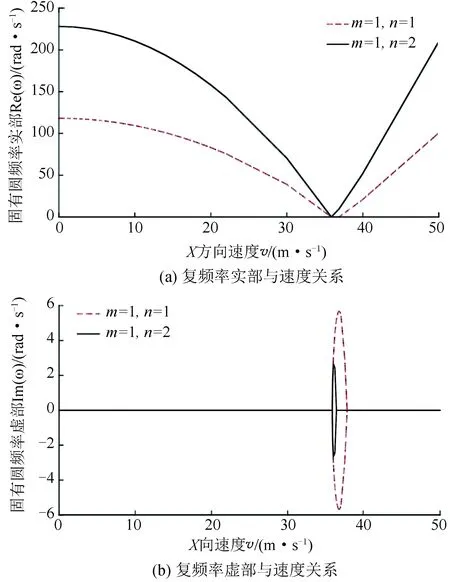
图6 两个刚性支承薄膜复频率与速度的关系Fig.6 Relationship between complex frequency and moving speed of membrane with two rigid supports
由图6可以看出,对于具有两个中间刚性支承运动印刷薄膜复频率ω11,速度在0~35.86 m/s内时,频率逐渐减小至0,在35.86~37.62 m/s内时,Re(ω)=0,Im(ω)出现,印刷薄膜系统处于发散失稳状态。当v>37.62 m/s时,印刷薄膜系统恢复稳定状态。对于印刷薄膜复频率ω12,速度在35.86~36.31 m/s内时,Re(ω)=0,印刷薄膜系统处于发散失稳状态;当v>36.31 m/s时,印刷薄膜系统恢复稳定状态。
图7所示为具有两个中间刚性支承印刷运动薄膜Y方向张力Ty分别为10 N/m和20 N/m时,薄膜的复频率ω与张力Tx之间的关系曲线。由图7可知,X向张力Tx为定值时,Y向张力越大,印刷薄膜的振动频率越大。当Ty为定值时,随着Tx增大,印刷薄膜振动频率实部增大。当Tx>5 N/m时,印刷薄膜振动频率实部与Tx为线性关系。0

图7 两个刚性支承薄膜复频率与张力Tx的关系Fig.7 Relationship between complex frequency and tension with two rigid supports
对于具有两个中间刚性支承的运动印刷薄膜,刚性支承的位置x1、x2会对印刷薄膜的振动频率有影响。令x1=a/10,分别求v=5 m/s及v=0时薄膜的振动频率与支承位置x2二次插值拟合的关系,如图8所示。

图8 薄膜的振动频率与支承位置的关系Fig.8 Relationship between transverse vibration natural frequency of membrane and supporting position
由图8可以看出,v=0情况下,x2在0~1.2 m范围内时,圆频率ω随x2的增大而减小;x2>1.2 m时,圆频率随x2的增大而增大。v=5 m/s情况下,0
4 结论
(1)运动速度v=0时,退化结果与文献[5]结果相一致,证明本文的计算方法是正确的;对理论分析结果进行实例计算。
(2)对于中间单刚性支承印刷运动薄膜,通过对其振动频率与运动速度、张力之间的关系的分析,获得了中间单刚性支承薄膜振动发散失稳的临界速度为35.855 m/s。轴向速度v=5 m/s时,张力范围为0~1.75 N/m时, 薄膜处于发散失稳状态;当Tx>1.75 N/m时, 系统又恢复稳定。
(3)对于具有中间两刚性支承的印刷运动薄膜,不同的刚性支承位置对薄膜的振动频率产生影响。v=0情况下,第二个刚性支承位置x2在0~1.2 m内时薄膜的振动频率随x2的增大而减小;x2>1.2 m时振动频率又呈增大趋势。v=5 m/s情况下,x2≤1.5 m时振动频率随x2的增大而减小;x2>1.5 m时振动频率呈现增大的趋势。薄膜轴向运动速度越低,支撑位置的变化对薄膜振动频率影响越明显。
