桥梁缆索高强钢丝均匀腐蚀及点蚀的规律

蒋 超，吴 冲，姜 旭

(同济大学 土木工程学院，上海 200092)

吊杆、拉索是索承式桥梁的重要受力构件，其耐久性直接影响着桥梁结构的安全性.近20年来，我国已有多座桥梁在服役15年内更换了吊杆或拉索，包括宜宾南门大桥、广州海印大桥、江阴长江大桥等[1].吊杆、拉索更换的原因与其内部钢丝严重的腐蚀现象有关[2-3].在腐蚀影响下，钢丝力学性能大幅下降，威胁着吊杆和拉索的使用安全.

缆索高强钢丝的腐蚀类型可以分为均匀腐蚀与局部腐蚀，局部腐蚀以点蚀为主.均匀腐蚀减小了钢丝截面，削弱了钢丝承载力等静力性能[4]；点蚀产生的蚀坑会形成裂纹萌生源，减小钢丝的疲劳寿命[5].因此，缆索高强钢丝腐蚀规律是研究钢丝力学性能衰退规律、建立力学性能时变模型的关键.

国内外很多学者对钢材料的腐蚀规律进行了研究.Melchers[6]提出了低合金钢腐蚀深度均值及标准差的双线性模型.Linder等[7]给出了碳钢在海水中均匀腐蚀深度的幂函数模型.曹楚南[8]给出了碳钢在我国部分地区大气下的腐蚀数据，发现同样遵循幂函数规律.点蚀方面，Aziz[9]、Shibata[10]采用极值统计分析和分块极值模型对最大点蚀深度进行了研究，该方法将试验数据按表面积进行分块，记录每块区域的最大点蚀深度，发现最大点蚀深度符合极值I型分布(Gumbel分布).Stewart等[11]采用点蚀系数——最大点蚀深度与均匀腐蚀深度的比值来定义点蚀程度，并给出了点蚀系数与不同分布形式的比较.上述研究为缆索高强钢丝均匀腐蚀及点蚀规律提供了理论基础和依据.但高强钢丝与上述研究对象材料不同，镀锌与冷拔过程极大地提高了钢丝的抗腐蚀能力，同时以往研究对象大部分采用板件形式，腐蚀规律是否适用于钢丝尚未可知.Li等[12]采用轮廓粗糙度仪对高强钢丝的腐蚀规律进行了研究，提出了高强钢丝均匀腐蚀及点蚀模型，但研究对象腐蚀程度较轻，该方法的适用范围和有效性尚未得到充分检验.

基于此，本文采用酸性盐雾试验得到了6组共30根不同腐蚀程度的钢丝试件，试件最大质量损失率超过15%，研究了钢丝均匀腐蚀深度随时间的发展规律.通过三维扫描技术，获取了腐蚀钢丝表面三维数据，探究三维数据的处理方法，分析了点蚀深度的分布规律，建立最大点蚀深度的预测模型，为定量研究钢丝力学性能衰退规律提供参考.

1 试验概况

1.1 试件设计

桥梁缆索高强钢丝试件采用江苏法尔胜缆索有限公司提供的B87MnQL型号钢丝盘条切割而成，钢丝化学成分如表1所示.试件直径为7 mm，镀锌层厚度约50 μm，长度取500 mm.由于考虑后续疲劳试验的要求，钢丝两端各包裹长度为100 mm的胶带以避免腐蚀，并内置标签记录编号，因此实际腐蚀区域长300 mm.试验采用冰乙酸混合氯化钠溶液的酸性盐雾进行人工加速腐蚀，按标准《人造气氛腐蚀试验 盐雾试验：GB/T 10125—2012》[13]进行，用来模拟桥梁结构可能处在的近海环境.腐蚀溶液的氯化钠质量浓度为(50±5)g·L-1，pH值为3.0，盐雾环境温度提高到(50±2)℃，以进一步提高钢丝腐蚀速率.

表1 缆索高强钢丝化学成分(质量分数)Tab.1 Chemical composition of high-strength bridge wires

钢丝试件分为A～F共6组，每组5根钢丝，盐雾腐蚀的时长随编号递增，具体腐蚀时长如表2所示.部分A组和F组的预腐蚀钢丝试件如图1所示.从图中可以很明显地看出，A组试件表面尚存在白色的锌锈，而F组试件表面已经堆满了疏松的红褐色铁锈，试件表面粗糙度较高.

表2 缆索高强钢丝腐蚀时长Tab.2 Corrosion time of high-strength bridge wires

a A组b F组

1.2 质量损失与均匀腐蚀深度计算

每组试件腐蚀完成后，立即从盐雾箱内取出，并按照标准《金属和合金的腐蚀 腐蚀试样上腐蚀产物的清除：GB/T 16545—2015)》[14]进行试件清洗.先在流水中用软毛刷进行轻微机械清洗，去除附着不牢固或疏松的腐蚀产物，然后在25 ℃室温下将试件浸在酸洗液中清洗10 min.最后，用自来水、蒸馏水、乙醇依次冲洗，吹风机吹干后冷却至室温.酸洗液采用规范[14]规定的铁或钢的清洗溶液，由500 mL浓盐酸、3.5 g六次甲基四胺以及适量蒸馏水配制而成.

考虑到无腐蚀钢丝试件在酸洗液中也会产生质量损失，试验设置3根未腐蚀的对照试件，故腐蚀钢丝的质量损失率可以表达为

(1)

式中：ηnk为腐蚀时间k时的第n根钢丝的质量损失率；mn0、mnk分别为第n根钢丝腐蚀前和腐蚀时间k时的质量；le为试件实际腐蚀长度，为300 mm；ln为试件总长度，为500 mm；mc1、mc2分别为对照试件初始质量和清洗后的质量.

根据钢丝试件的质量变化，均匀腐蚀深度可通过质量与面积损失的关系推导得出

(2)

式中：ρ为材料密度，考虑到钢和锌密度相近，且镀锌层未耗尽时就会产生钢、锌的共同腐蚀，ρ统一取钢的密度；D为钢丝直径；du,nk为腐蚀时间k时的第n根钢丝的均匀腐蚀深度.当du,nk≪D时，均匀腐蚀深度可简化为

(3)

1.3 三维扫描及数据处理

试验采用北京天远三维科技有限公司生产的照相式三维扫描仪对钢丝试件进行扫描，扫描仪型号为OKIO-5M，仪器最高测量精度为5 μm，平均采样间距最小为40 μm，满足分析的精度要求.扫描步骤为：试件涂抹显像剂并干燥，通过支架将腐蚀钢丝试件固定，调整扫描精度开始扫描，扫描好后将试件翻转90°继续扫描，从而获得整根试件的表面三维数据.钢丝扫描数据通过三维软件Geomagic Studio显示的图像如图2所示.

a 整体b 局部

表面三维数据以三角形网格的方式存储于文件中.该文件无法直接输出点坐标，需要使用逆向工程软件进行处理.本文采用软件NX Imageware进行点云处理，并结合软件AutoCad获取点坐标.具体步骤如下：步骤1，通过平移和旋转调整钢丝试件，采用平面径向上切割三角形网格，生成每个切面上的点云；步骤2，采用内插法曲线，通过点云生成切面的轮廓曲线；步骤3，通过轮廓曲线构建均匀分布的点云，导出成dxf文件，通过软件AutoCad的数据提取功能生成点云坐标.

通过步骤2、3，可以将切面上数量众多且间距不一的点云转换为给定数量的等间距点云.本文径向上切割的间距为0.25 mm；每个轮廓曲线上构建120个点，即截面每隔3°取1个点.

2 试验结果分析

2.1 均匀腐蚀深度

A～F组试件均匀腐蚀深度的统计特性如表3所示.随着腐蚀时间的增加，钢丝均匀腐蚀深度的均值增大，变异系数减小.A组试件的变异系数远大于其他组，原因是一方面镀锌层尚未完全耗尽，部分钢丝基体与尚存的镀锌层同时受到腐蚀，腐蚀速率不稳定，腐蚀深度不确定性较大；另一方面是钢丝均匀腐蚀深度较小，对腐蚀深度的波动更敏感.

所有钢丝试件均匀腐蚀深度随腐蚀时长变化的关系如图3所示，两者呈非线性关系，均匀腐蚀深度的增长速度逐渐减慢.采用幂函数来拟合试验数据，得到试件均匀腐蚀深度随腐蚀时长的变化关系为

du(t)=1.009t0.764

(4)

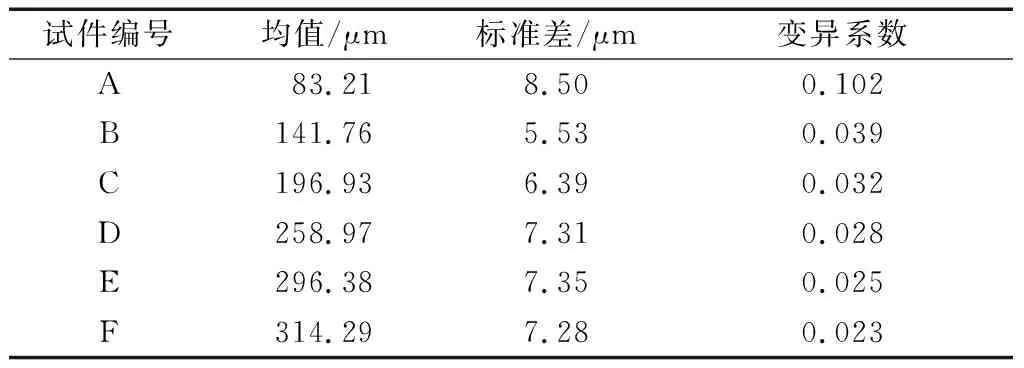
表3 均匀腐蚀深度统计特性Tab.3 Statistical properties of uniform corrosion depth

图3 均匀腐蚀深度随腐蚀时长变化关系Fig.3 Uniform corrosion depth versus exposure time

拟合曲线以及95%的置信区间如图3所示.可以看出，缆索高强钢丝在腐蚀下均匀腐蚀深度同样遵循幂函数规律.

2.2 点蚀深度

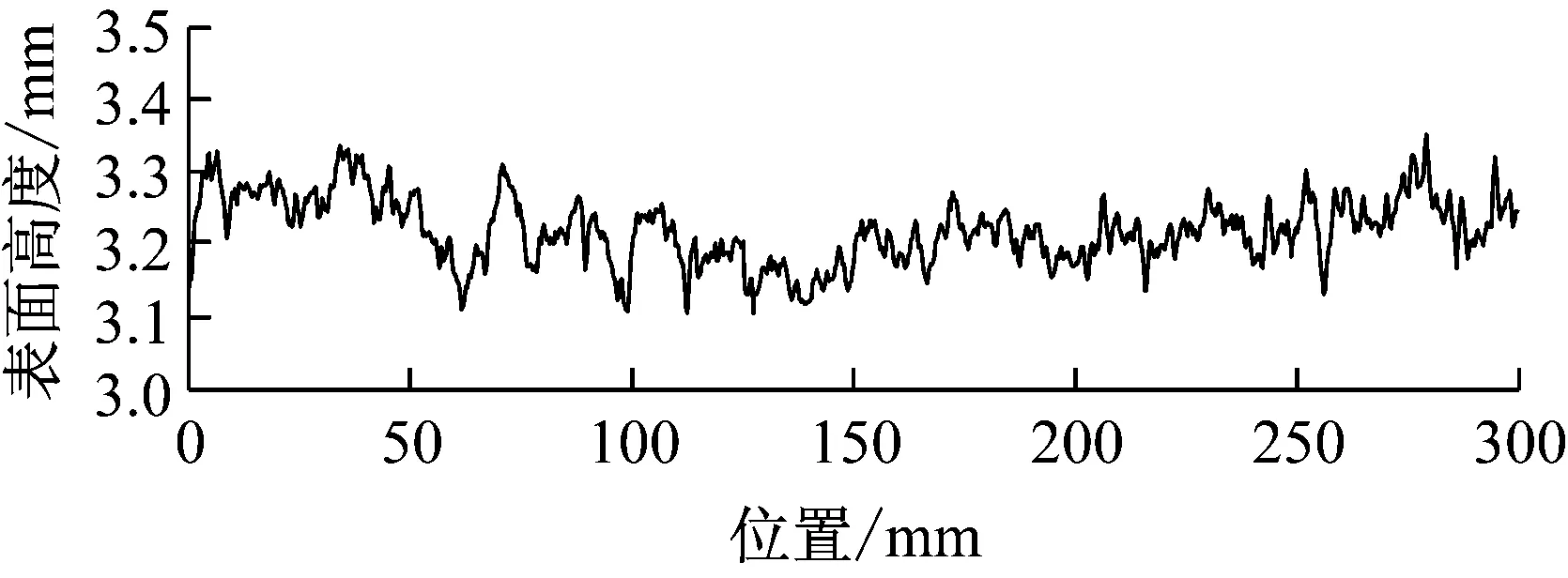
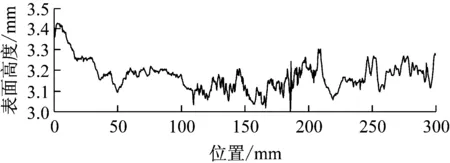
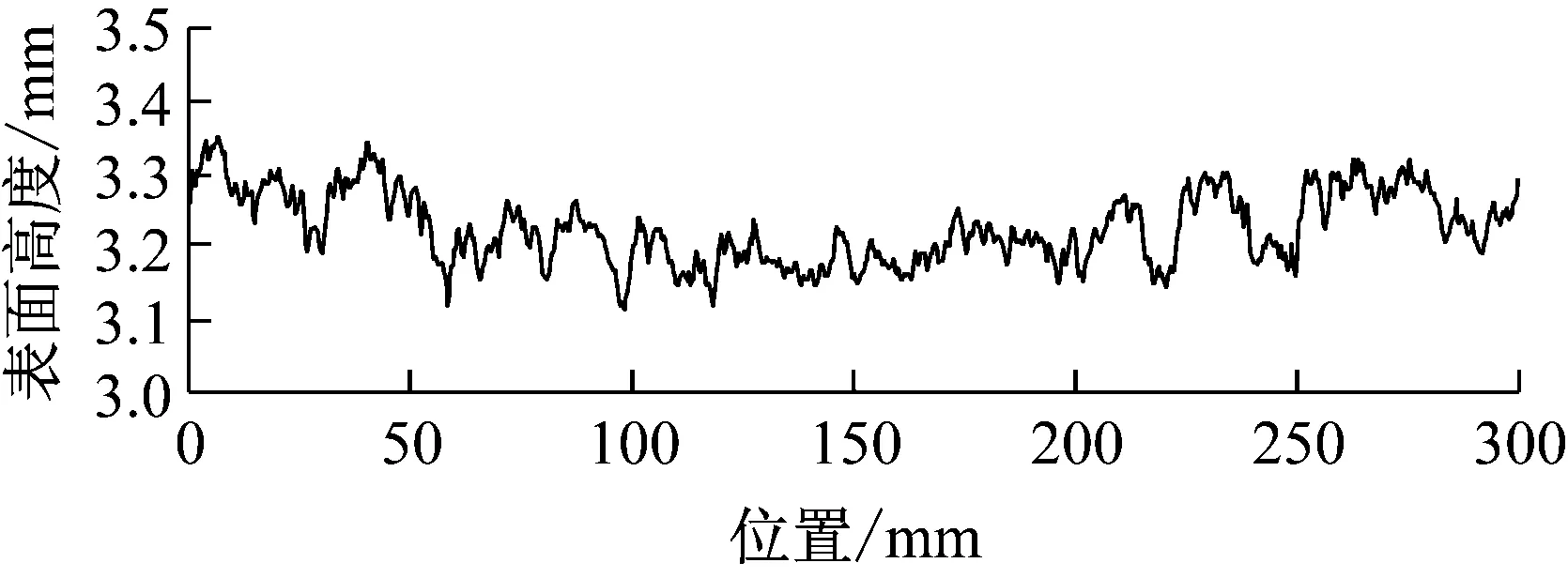
根据径向与周向上的等间距点云坐标，可以得到试件任意角度下的表面轮廓线.以试件F-1为例，所选角度为0°、90°、180°、270°的轮廓线如图4所示，角度为钢丝圆周面上的旋转角度，取靠近扫描仪的水平方向为0°.从图中可以看出，同一根钢丝在不同角度下的腐蚀情况相差较大，角度为0°、180°的表面钢丝腐蚀情况好于角度为90°、270°的表面.因此，仅根据有限个角度下的表面轮廓线无法精确计算钢丝的腐蚀情况.

基于每个试件120条轮廓线，可以得到腐蚀钢丝的腐蚀深度等高线.以试件C-1为例，等高线如图5所示.从图中可以看出明显的蚀坑分布，腐蚀时长为997 h时，部分蚀坑深度已超过300 μm.

a 0°

b 90°

c 180°

d 270°图4 试件不同角度下的表面轮廓线Fig.4 Surface profiles

图5 试件C-1腐蚀深度等高线Fig.5 Contour of corrosion depth

每个试件120条轮廓线构成了试件的表面轮廓二维矩阵，对矩阵进行蚀坑识别，可以得到蚀坑长、宽、深度的信息，从而对蚀坑三维进行统计分析.经过假设检验发现，正态分布对于各组试件的点蚀深度均能通过显著性水平为95%的K-S检验.正态分布的概率密度函数表达式为

(5)

式中：μ和σ均为分布参数.不同腐蚀时长试件的点蚀深度分布见图6.图中点蚀深度正态分布模型的概率密度函数向右移动且宽度逐渐变大，表明点蚀深度的均值和离散度随腐蚀程度的增加而增大.

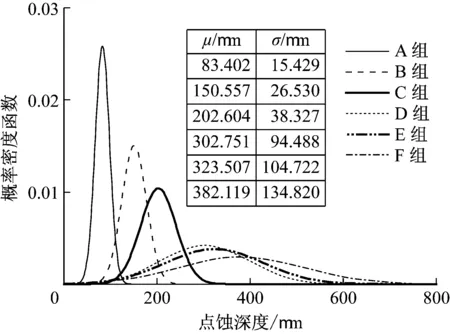
图6 试件点蚀深度分布Fig.6 Distribution of corrosion depth

试件分布参数与质量损失率的关系如图7、8所示.考虑到质量损失率为0%时分布参数均为0，因此，同样采用幂函数来拟合分布参数.表达式分别为

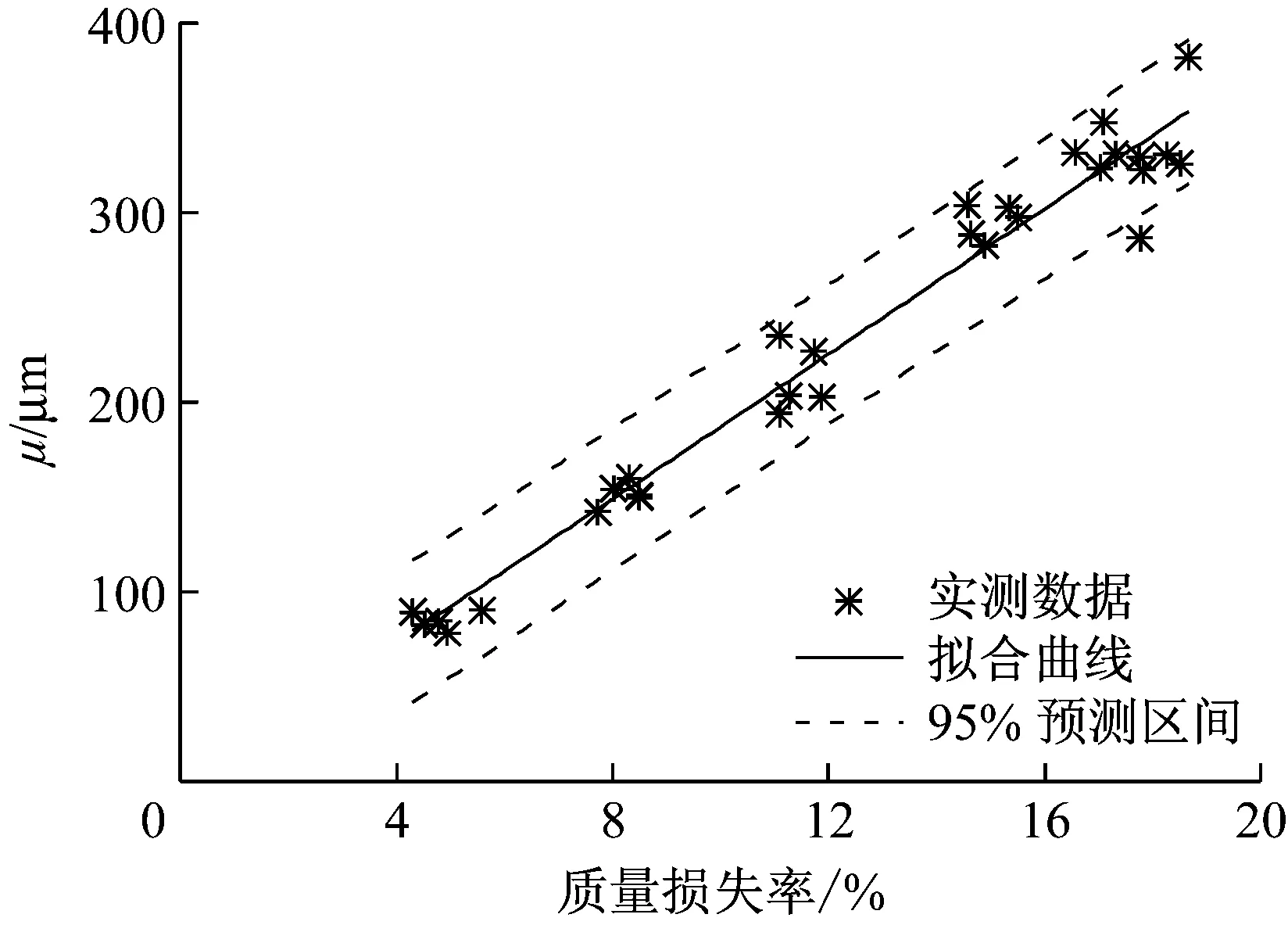
图7 μ与质量损失率的关系Fig.7 μ versus weight loss

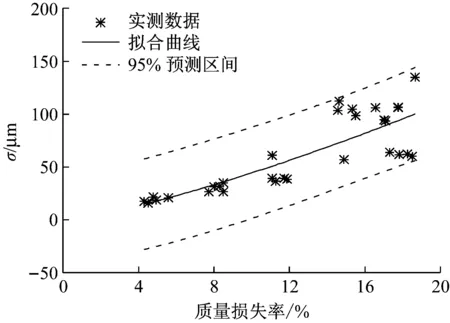
图8 σ与质量损失率的关系Fig.8 σ versus weight loss

(6)

式中：η为质量损失率.

3 最大点蚀深度模型

3.1 模型推导

最大点蚀深度是影响腐蚀构件疲劳寿命的决定性因素，准确的最大点蚀深度预测模型是建立腐蚀构件疲劳衰退模型的基础.根据上文分析可知，缆索高强钢丝点蚀深度服从正态分布，分布参数可通过钢丝质量损失率结合式(4)、(5)计算得到.点蚀深度的概率密度函数如式(3)所示，分布函数的表达式为

(7)

最大点蚀深度模型与点蚀深度模型的最值模型等价，可以通过点蚀深度模型的尾部分布推导

(8)

当x→+∞时，

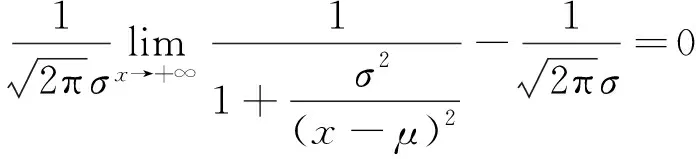
(9)

所以正态分布的尾部深度服从极值I型分布(Gumbel分布)[15].极值I型分布的分布函数形式为

(10)

式中：a为尺度参数；b为位置参数.

当蚀坑个数n较大时，可以解得模型参数为[16]

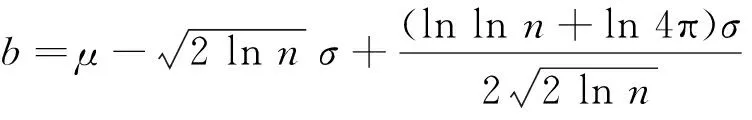
(11)

蚀坑个数n经试验结果统计分析可得

(12)

式中：L为钢丝长度，m；η为质量损失率.

3.2 模型验证

根据各试件点蚀深度模型的参数及蚀坑个数，可以计算得到试件最大点蚀深度dp max服从的极值I型分布参数.在已知分布下，通过蒙特卡洛模拟生成符合该分布的1 000个随机数，模拟值与实测最大点蚀深度如表4所示.从表中可以看出，30个试件中仅有4个试件的最大点蚀深度超出了模拟生成的最大点蚀深度最值区间，且误差均小于10%，分别为0.68%、-0.37%、-9.10%和-7.89%.其余试件中，13个试件处于模拟的95%区间内，13个试件处于最值区间内.表4表明，本文推导得出的最大点蚀深度模型与实测值吻合良好.

3.3 实例分析

以杭州湾大桥北航道桥某拉索为例，该拉索截面包含109根钢丝，钢丝长98 m，直径为7 mm.分析中将拉索护套出现轻微破损、护套内开始出现水气、钢丝与外部腐蚀环境开始接触的时间点设为零点.

杭州湾大桥拉索钢丝处于海水潮湿环境下.镀锌层在海水飞溅区的腐蚀速率为13.38 μm·年-1，50 μm厚的镀锌层将于3.74年后耗尽[17].设实际环境与试验环境的换算系数为k，即实际环境中1年相当于试验环境小时k，那么

du(t)=1.009(3.74k)0.764=50 μm

k=44.24 h

(13)

因此实际环境中，钢丝的均匀腐蚀深度如图9所示，腐蚀30年后，拉索高强钢丝的均匀腐蚀深度接近250 μm，钢丝直径减小7.01%，截面横截面积减小13.53%.

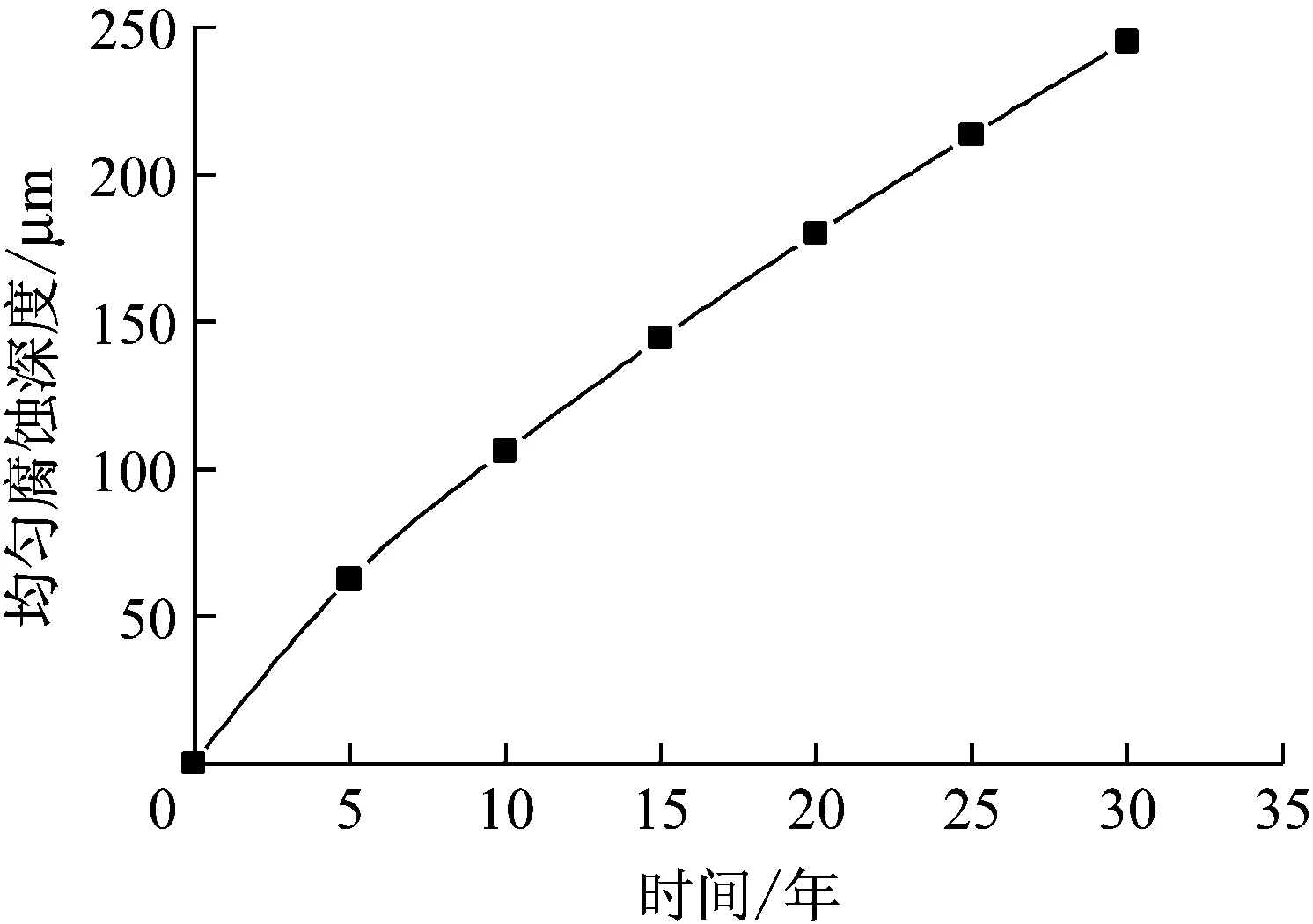
图9 拉索钢丝均匀腐蚀深度Fig.9 Uniform corrosion depth

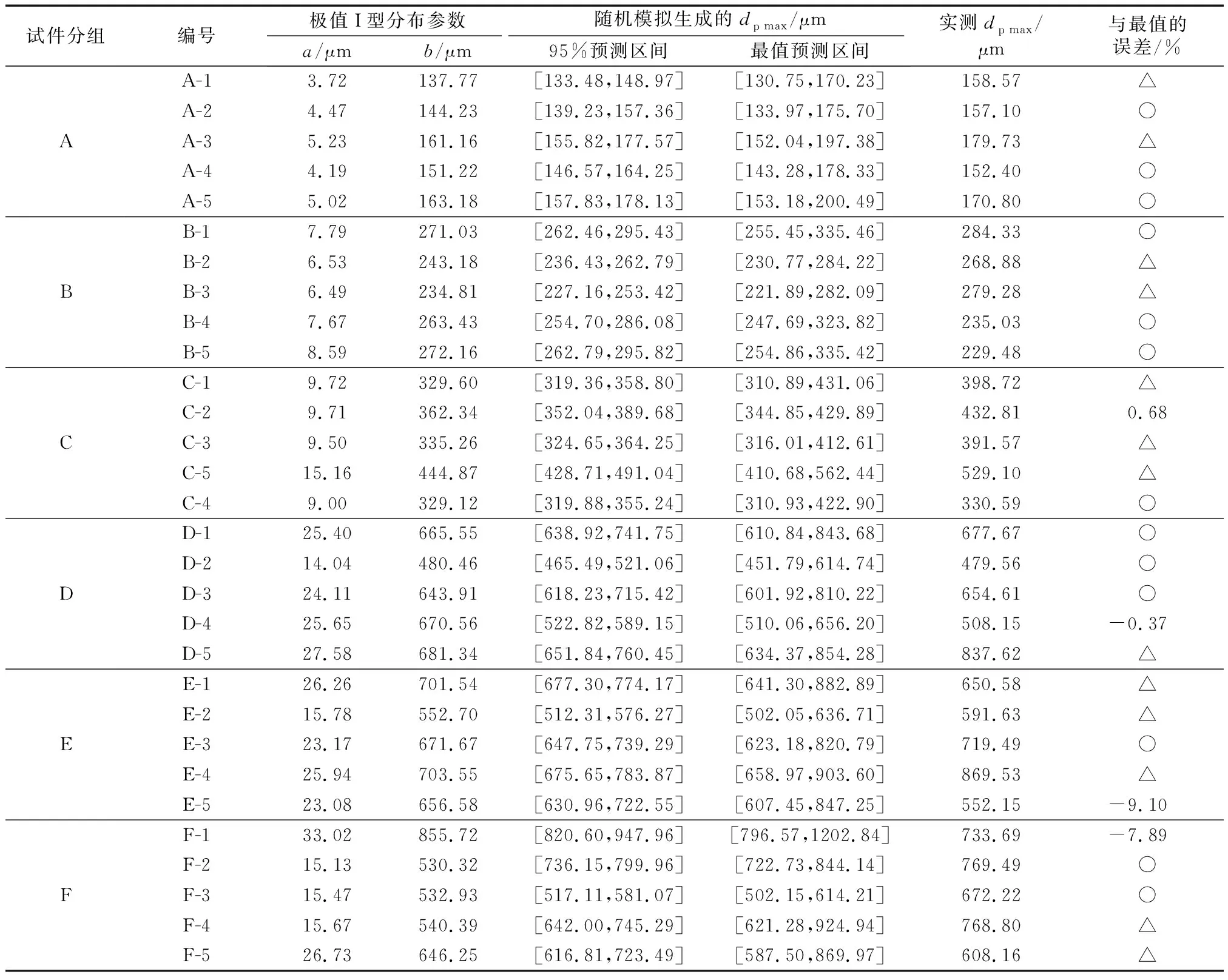
表4 预腐蚀缆索高强钢丝最大点蚀深度预测结果Tab.4 Model prediction of maximum pitting depth of pre-corroded bridge wires

注：△代表实测值处于预测最值区间内，但在预测95%区间外；○代表实测值处于预测95%区间内.

根据式(6)，可以计算得到不同腐蚀年份下钢丝点蚀深度的模型参数，结合式(11)和(12)，即可求得最大点蚀深度的模型参数.杭州湾大桥拉索钢丝在实际环境下的最大点蚀深度分布如图10所示，腐蚀30年后，拉索高强钢丝的最大点蚀深度超过550 μm.

图10 拉索钢丝最大点蚀深度分布Fig.10 Distribution of maximum pitting depth

4 结论

本文采用酸性盐雾试验制备了不同腐蚀程度的桥梁缆索高强钢丝，通过质量分析、三维扫描等手段，研究了腐蚀钢丝均匀腐蚀及点蚀的演变规律，得到如下结论：

(1)缆索高强钢丝在腐蚀下均匀腐蚀深度随腐蚀时长的变化同样遵循幂函数规律，均匀腐蚀深度的变异系数随腐蚀时长减小.

(2)明确了钢丝三维扫描的数据处理方法，钢丝的点蚀深度服从正态分布，建立了以质量损失率为变量的点蚀深度模型.

(3)建立了钢丝最大点蚀深度预测模型，试验结果与预测值的对比验证了模型的准确性.

(4)以实桥为例，分析了在实际腐蚀环境下拉索钢丝均匀腐蚀深度以及最大点蚀深度的变化，为定量研究拉索腐蚀后的使用寿命提供了参考.