山海关旅游海滩生态修复工程水动力变化特性
2019-01-08匡翠萍董博灵谢华浪杨燕雄
匡翠萍,董博灵,谢华浪,杨燕雄
(1. 同济大学 土木工程学院,上海 200092;2. 珠江水利科学研究院,广东 广州 510611;3. 河北省地矿局第八地质大队,河北 秦皇岛 066001)
山海关位于河北省秦皇岛市,是我国著名的旅游区.其中,海滩旅游占有重要地位[1-2],长达14 km的海岸线是山海关最重要的旅游资源之一.然而近些年来,滩面下蚀[3]、岸线后退[4]、砂粒粗化[5]等海滩侵蚀问题层出不穷,也因此成为了山海关海滩旅游发展的瓶颈.时间尺度上,海滩侵蚀问题可以分为两类:一是短暂的、迅速的侵蚀过程,这种侵蚀过程通常是由罕见的强浪和风暴潮引起的,相关研究内容包括侵蚀过程[6]、侵蚀量级[7]、累积效应[8]等;二是持续的、缓慢的侵蚀过程,这种侵蚀过程一般是由海域整体的动力不平衡引起的,相关研究内容包括侵蚀的地域差异[9]、侵蚀区域的水动力分析[10]、海平面上升引起的侵蚀[11]等.相较于前者,海域动力不平衡引发的海滩侵蚀由于其不可逆性而危害更大.为了改善山海关海域水动力状况,保护海滩旅游资源,山海关旅游海滩修复工程由此展开,而同时工程的建设必然对周边环境产生影响[12-14].目前,针对秦皇岛市的海滩侵蚀问题,如金梦海湾[15]、北戴河东海滩[16]、中海滩和西海滩[17],采取了抛沙养滩和布置离岸潜堤的措施,使海滩整体趋向稳定.Kim等[18]通过野外监测证实了水下人工鱼礁对韩国东侧海滩具有保滩促淤的作用.为了探究山海关旅游海滩生态修复工程对海域水动力的影响,本研究采用Delft3D数值模拟软件建立波流耦合数学模型,模拟和预测工程建设引起的水动力变化特性.
1 数学模型
1.1 工程概况
山海关旅游海滩生态修复工程如图1所示.针对白鹭岛至唐子寨岸段海滩,近岸主要采取滩肩补沙,并辅以离岸潜堤阻挡波浪,并在后缘设计滨海景观廊道和人工覆植沙丘等生态工程.其中,补沙岸线长度为2 km,沙滩宽度在原有基础上增加30~50 m,沙粒的中值粒径为0.46~0.69 mm,采用交会型剖面的形式;两座离岸潜堤分别距岸240 m和350 m,长300 m,宽8.4 m,堤顶高程为-1.0 m,使用人工鱼礁的形式进行布置,以尽量减小工程对海域生态的负面效应;滨海景观廊道主要包括自行车道、绿化带和木栈道,形成区域海岸带整体建设的旅游功能与生态环境相互平衡.基于Delft3D建立波流耦合数学模型,分析研究工程造成的海域水动力变化特征,为这类旅游生态修复工程的设计与建设提供一定科学依据.
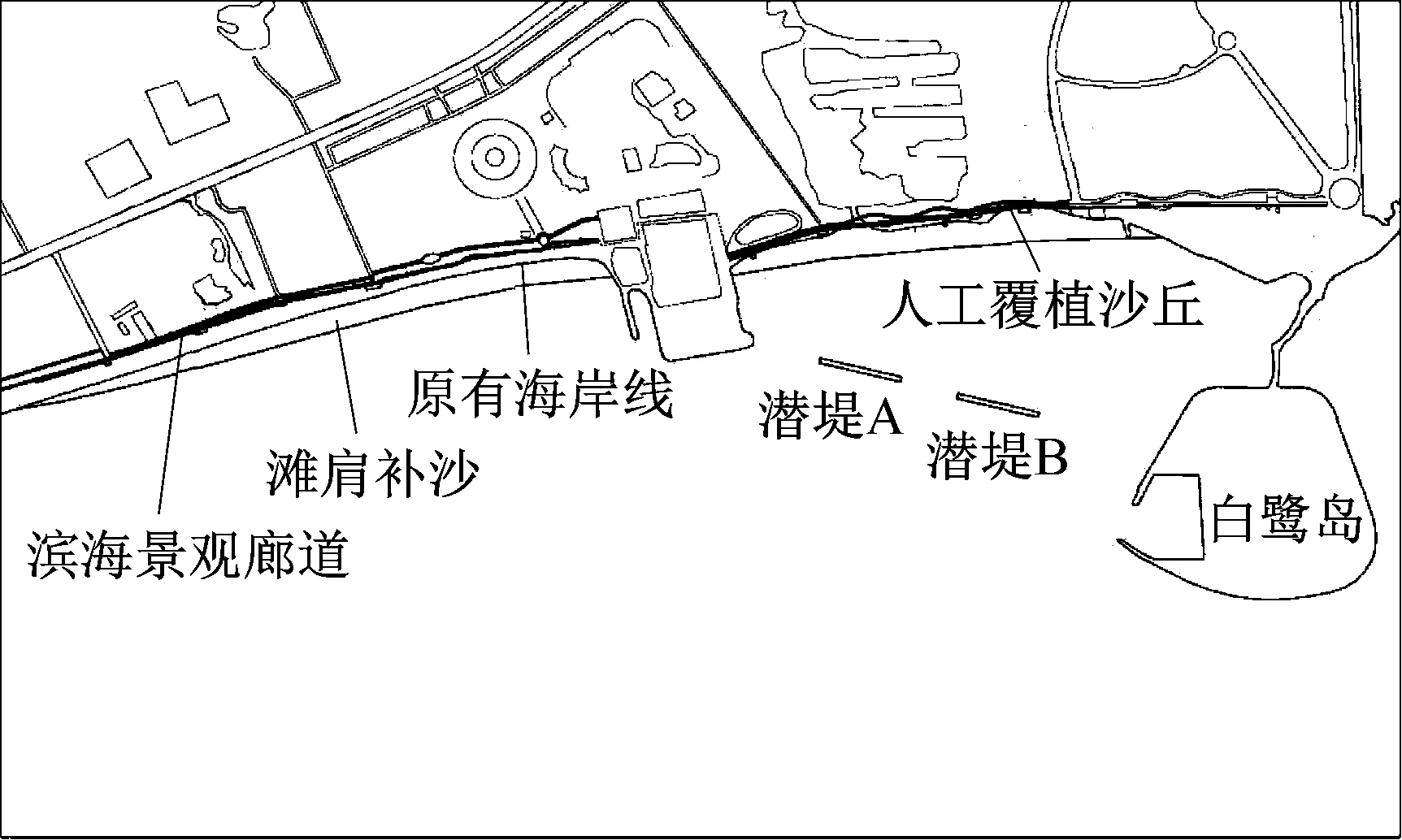
图1 工程总体平面布置图Fig.1 General engineering layout
1.2 模型方程
Delft3D是由WL Delft Hydraulics(荷兰Delft水力学研究所)开发的一套多功能的数值模拟软件,主要应用于河流、河口、海岸等自由地表水环境地区的水动力、水环境、泥沙运动等方面的科学研究.
Delft3D-FLOW潮流模型的基本方程采用浅水假定和Boussinesq近似,由不可压缩的三维Navier-Stokes方程推导而来.
水深平均连续方程如下:
(1)
ξ和η为正交曲线坐标系的两个坐标方向,ξ和η方向的动量方程为
(2)
(3)
式中:ζ为基准面以上的水位;t为时间;Gηη、Gξξ为正交曲线坐标系与笛卡尔坐标系之间的转换系数;d为基准面以下的水深;u、v分别为ξ和η方向的水深平均流速;w为z方向的流速;f为柯氏力系数;ρ0为水的相对密度;Pξ、Pη分别为ξ和η方向压力梯度;Fξ、Fη分别为ξ和η方向上紊动引起的雷诺应力;Mξ、Mη分别为ξ和η方向上泄流或取水、构筑物、波浪应力等外部作用引起的动量变化;vV为垂向涡黏系数;Q为单位面积的源汇项,包括降水、蒸发、流入和流出的水流引起的水量变化.
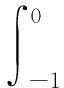
(4)
式中:qin和qout分别为单位体积的源项和汇项;P为降水引起的源项;E表示蒸发引起的汇项.
Delft3D-WAVE波浪模型采用第三代SWAN波浪模型,即采用二维波浪密度谱描述随机波浪,其波浪频谱的变化以谱平衡方程描述,在笛卡尔坐标系下,谱平衡方程为
(5)
式中:N为波浪作用密度;σ为相对频率;θ为波浪传播方向;cx、cy、cσ和cθ分别是x、y、σ、θ方向上的波浪传播速度;式中第1项为波浪作用随时间的变化,第2、3项为波浪传播随空间变化,第4项为地形和水流引起的多普勒频移效应,第5项表示地形和水流引起的波浪折射;S是源项(包括风生浪、耗散、非线性波和波浪破碎等过程),其中,风能输入可表示为
Sin(σ,θ)=A+BE(σ,θ)
(6)
式中:A和B取决于波浪的频率、角度以及风的速度、角度;E(σ,θ)为波浪能量谱密度.
1.3 模型参数
由于工程区域较小,为保证足够的计算精度,采用渤海大模型、秦皇岛中模型和山海关小模型三重嵌套的方式进行计算,如图2所示.大模型的网格数为450×350,网格最小空间步长约为2 km;中模型的网格数为200×330,网格最小空间步长约为350 m;小模型的网格数为285×460,网格最小空间步长约为50 m.

图2 大、中、小模型网格Fig.2 Meshes of big, middle, and small models
渤海大模型海域开边界由大连老虎滩和烟台两个潮位站所测得的潮位过程所控制,秦皇岛中模型的边界包括西边界、南边界和东边界3条海域开边界和1条陆地闭边界,其潮位边界条件由大模型提供,波浪边界条件由实测和模型率定综合得到.侧固边界采用不可滑移条件,利用动边界处理干湿交换过程.山海关小模型边界的边界处理与秦皇岛中模型相同.大模型和中模型的地形数据采用近10年内最新的地形数据,小模型的地形数据采用河北省地矿局第八地质大队于2015年12月(工程前)和2016年9月(工程后)两次高密度(测量点间距小于3 m)的水下地形测量数据.水平紊动黏滞系数取为15 m2·s-1,曼宁系数取均值为0.015,计算时间步长取1.0 min,初始水位为平均海平面.
2 模型验证
通过将当前时刻的Delft3D潮流模型与波浪模型输出的计算结果,分别作为下一时刻的Delft3D波浪模型与潮流模型的输入条件,实现两个模型的相互耦合,并利用耦合后的数学模型,进行模型验证.河北省地矿局第八地质大队于2015年9月23日、24日在工程海域附近测量得到相关实测数据,测站分布如图3所示.根据2015年9月23日0:00
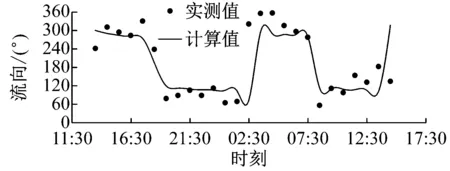
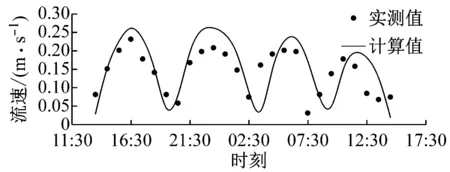
至9月25日0:00秦皇岛和山海关潮位站的潮位过程资料进行潮位验证,验证结果见图4.根据2015年9月23日13:00至9月24日14:00测站BLD01、BLD02的实测潮流数据进行潮流验证,验证结果见图5.

图3 测站点分布Fig.3 Positions of measurement points
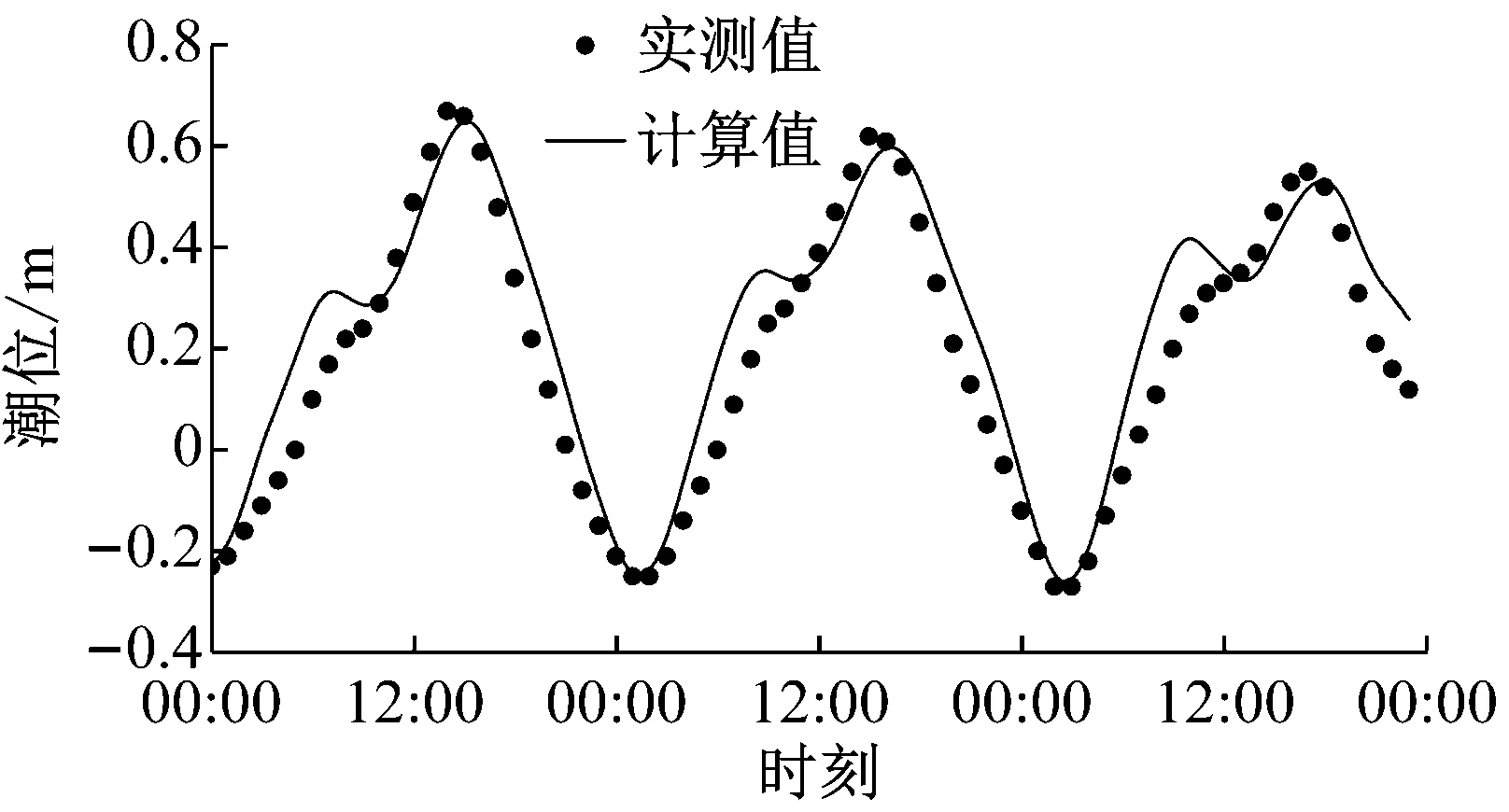
a 秦皇岛
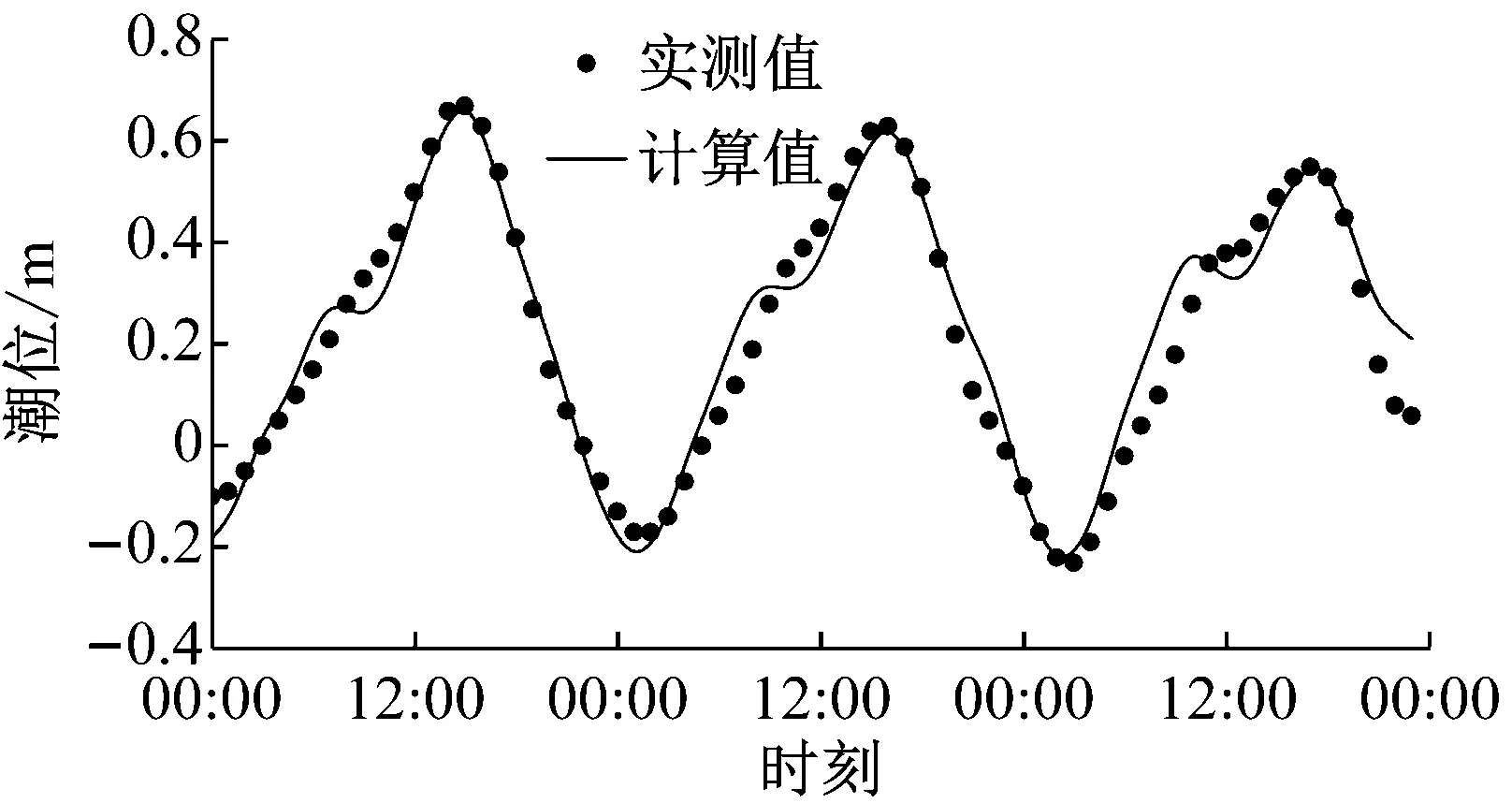
b 山海关图4 2015年9月23日0:00至9月25日0:00秦皇岛和山海关潮位站潮位过程验证Fig.4 Tidal level validation at Qinhuangdao and Shanhaiguan
由于研究区域位于半日潮无潮点和日潮波腹区,潮汐变化复杂;实际测量正值小潮日,潮流流速较小,易受其他环境因素干扰,因此在个别时段,潮流流速的计算值和实测值存在一定的误差.
Wilmott统计学方法[19]考虑了实测值与实测平均值的偏差、模型计算值和实测平均值的偏差这两者的相关程度,其计算方法为
(7)
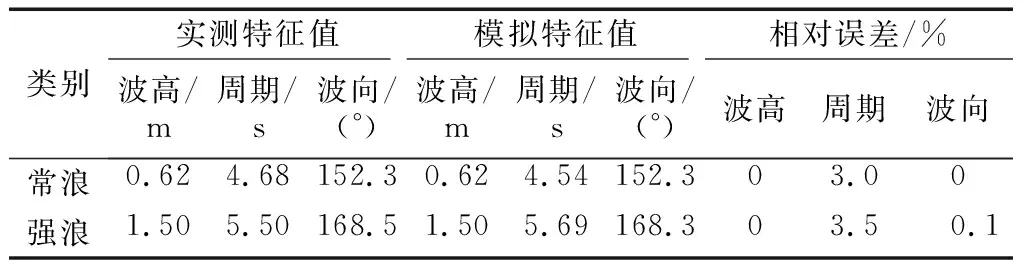
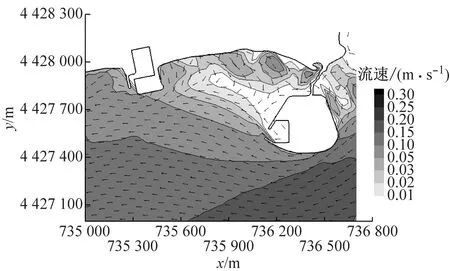
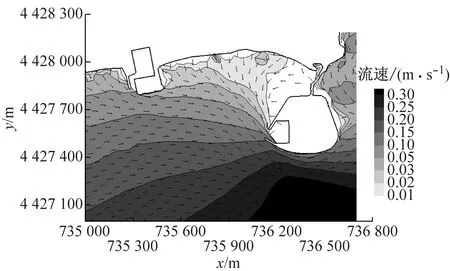
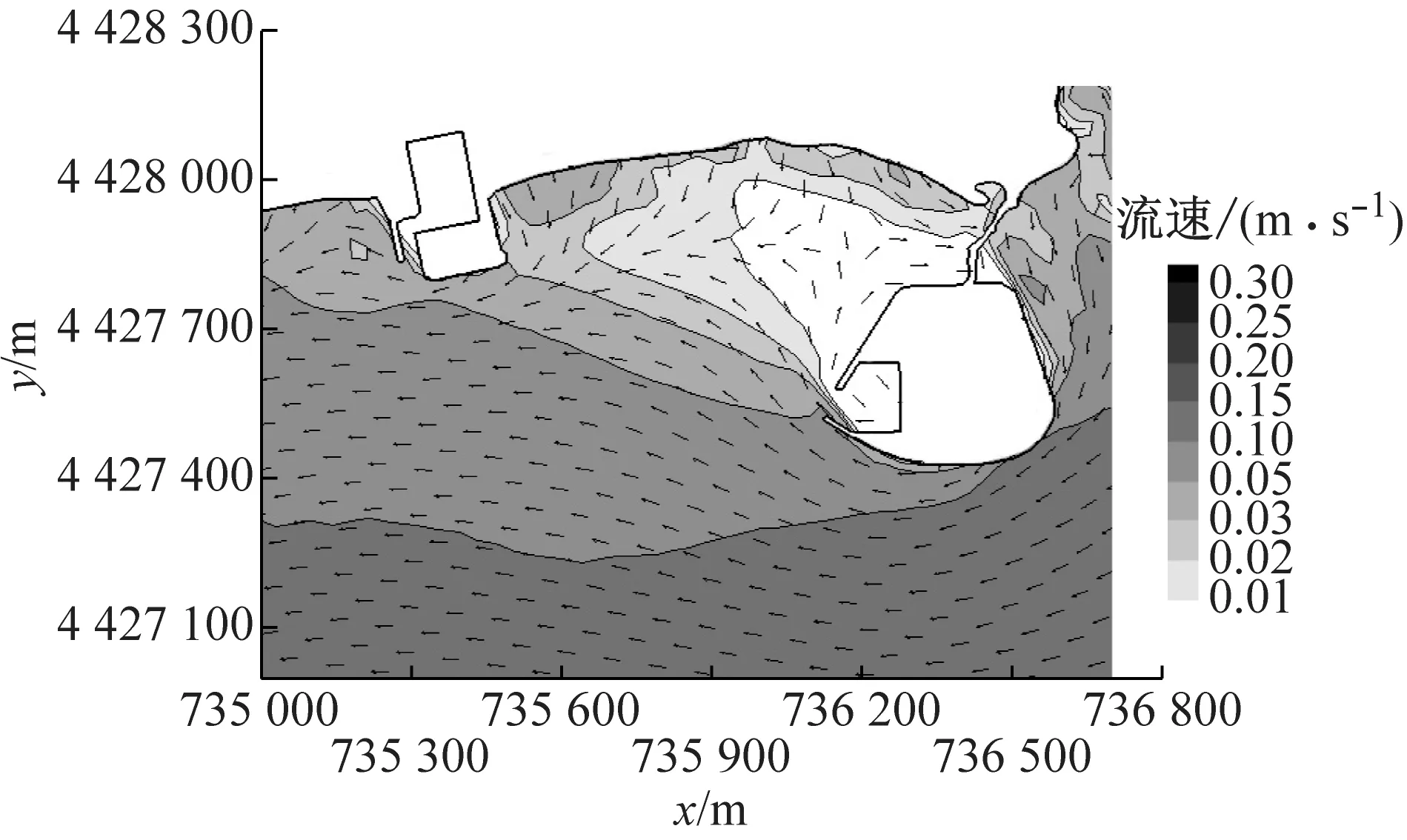
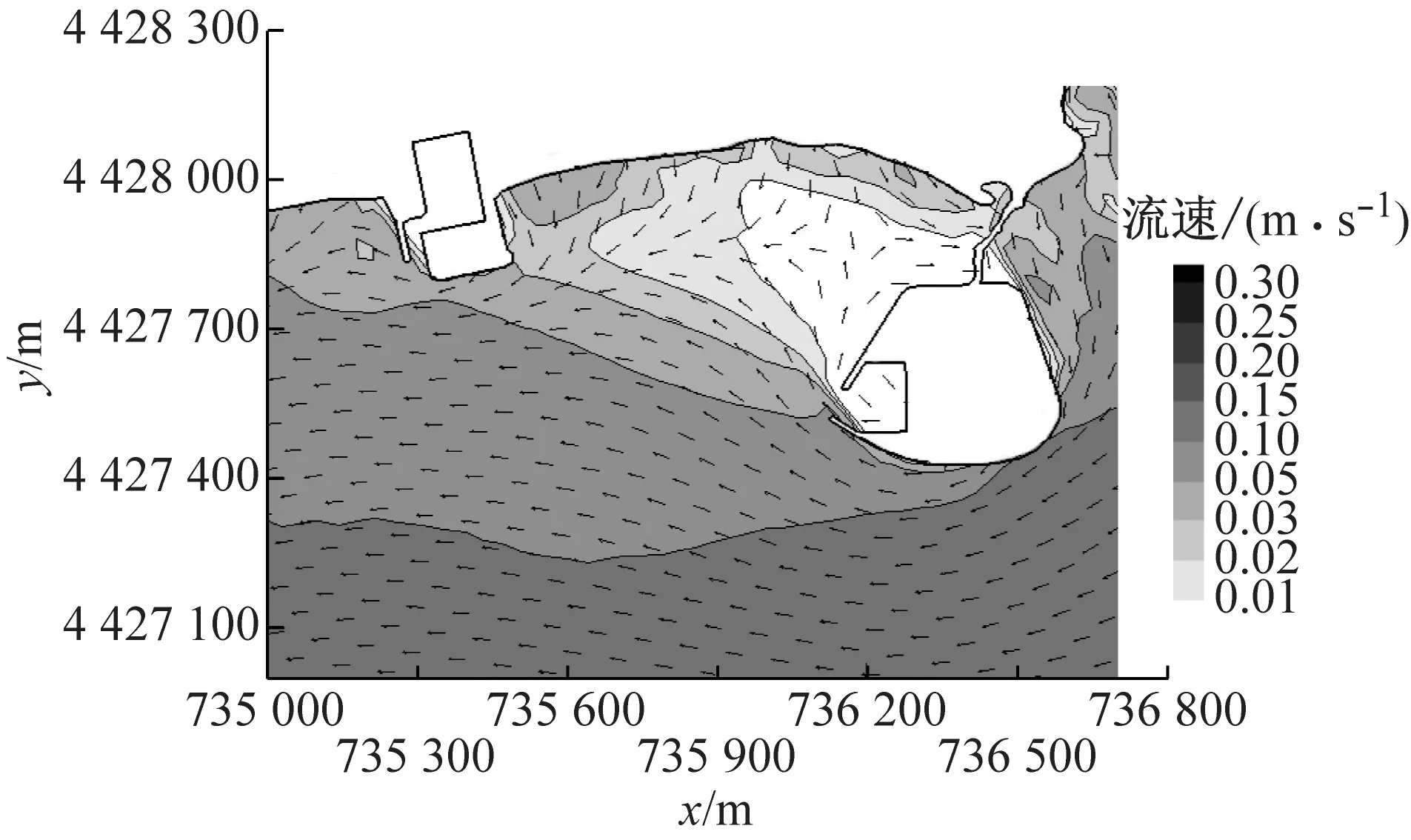
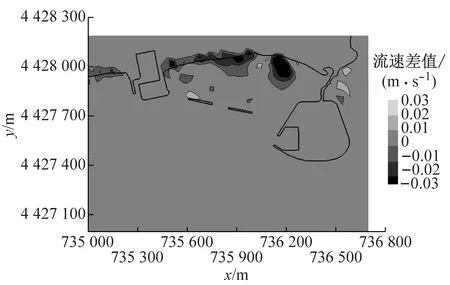
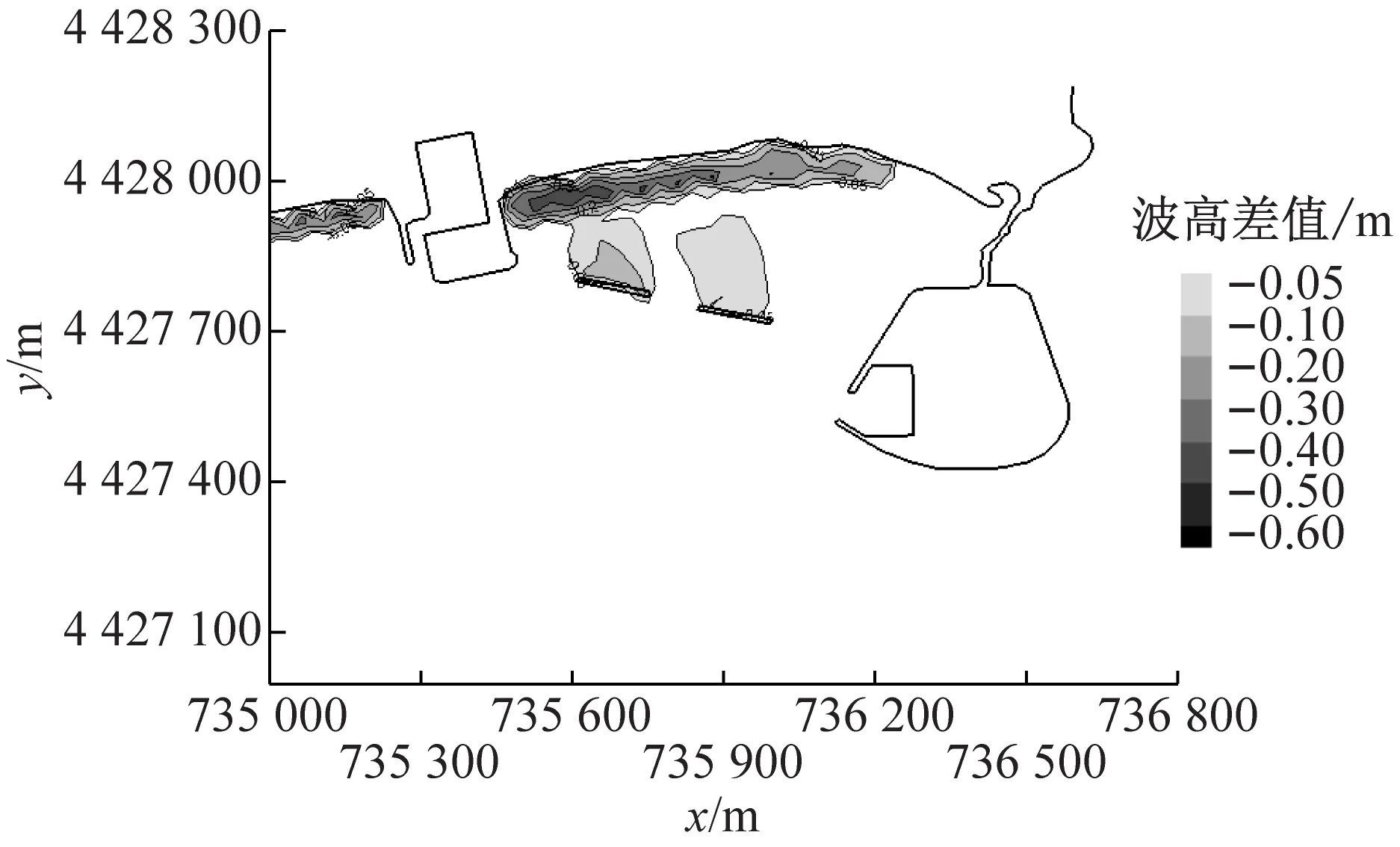
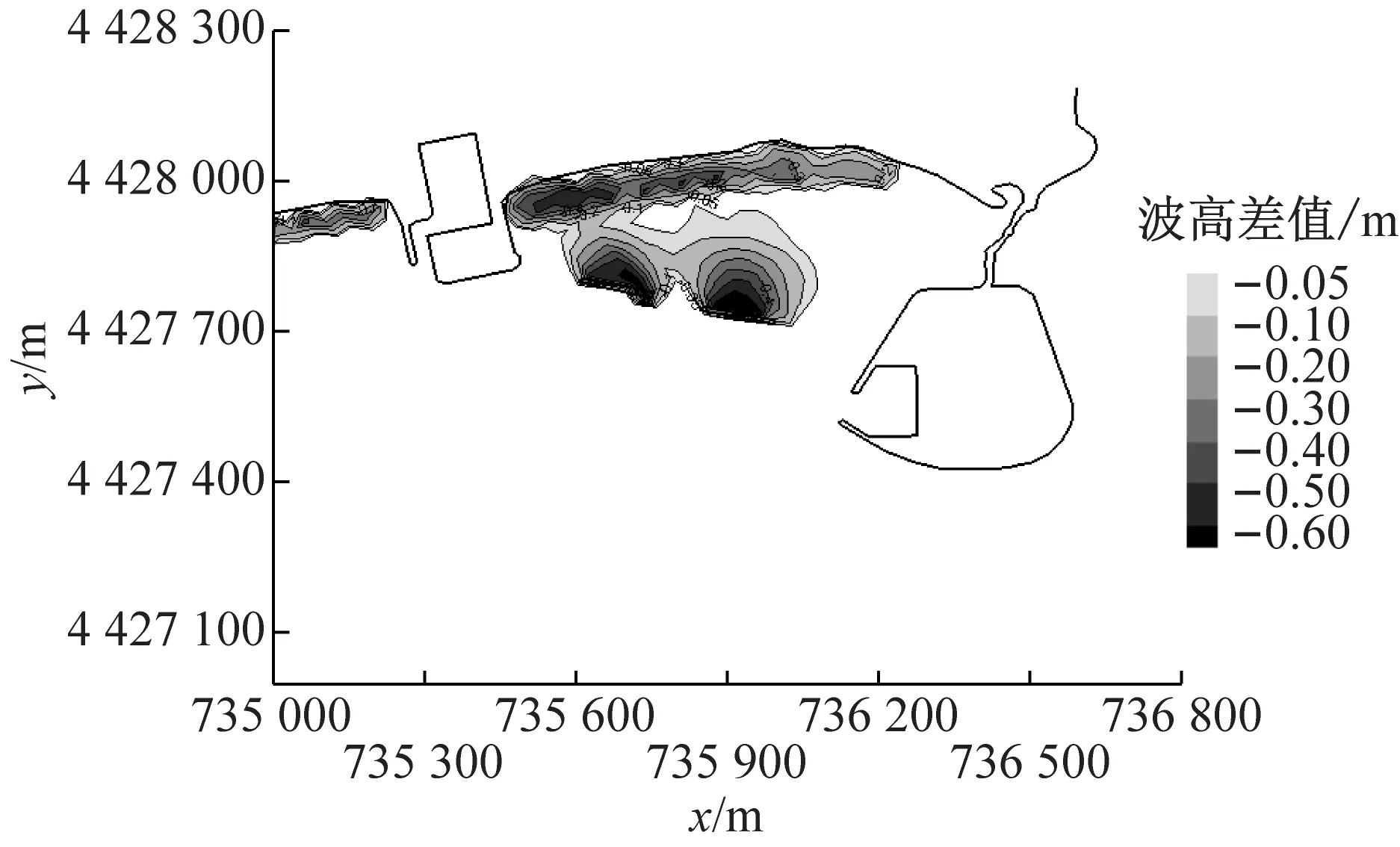
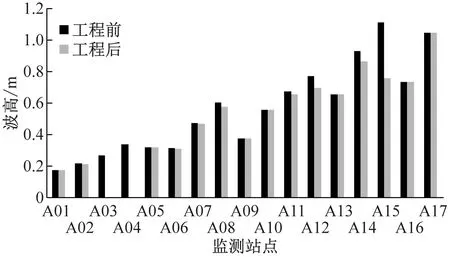
式中:s>0.65时结果为极好;0.5 a BLD01测站流速 b BLD01测站流向 c BLD02测站流速 d BLD02测站流向图5 2015年9月23日13:00至9月24日14:00测站BLD01和BLD02的垂向平均流速和流向过程验证Fig.5 Depth-averaged velocity and direction validation at BLD01 and BLD02 表1 Wilmott统计学方法得到的模型评价结果Tab.1 Model evaluation result by descriptive statistic of Wilmott 可以看出,潮位和潮流验证的s值评价均为极好.由此可知,模型模拟值与实测值吻合较好.该模型可以用于模拟该区域实际的水动力. 从动力角度分析,波浪的动力作用与波高的平方成正比.因此,选取以波高平方为依据的波浪统计值作为具有长期代表作用的常浪.由秦皇岛波浪测站2011年3月至9月的资料,可得常浪条件为波高H1/3=0.62 m,周期T=4.68 s,波浪方向为152.3°;另外,取2011年的最大有效波高作为强浪,故强浪条件为H1/3=1.50 m,T=5.50 s,波浪方向为168.5°.经过对模型的率定,模拟得到常浪和强浪波况下的波高、周期、波向的特征值均与实测特征值相一致(见表2). 表2 常浪和强浪波况下的实测值与计算值对比Tab.2 Comparison of measured value and model result of normal and strong wave 利用经过验证的波流耦合模型,得到了山海关旅游海滩修复工程建设前后的潮流场和波浪场,对工程前后的水动力进行分析和比较,得到旅游海滩生态修复工程手段的成效. 山海关海域位于M2和S2分潮的无潮点附近[20],潮差较小,水动力较弱,潮汐为正规全日潮,潮流为正规半日潮.涨潮流基本为WSW向,落潮流基本为ENE向,潮流为典型的往复流.以2015年6月夏季典型潮型为例,工程前山海关海域大小潮涨、落急时刻潮流场如图6所示(图中的坐标系统为北京54坐标系统).总体上,山海关海域大小潮涨、落急流速大小相差不大,涨潮流向大致为SW向,落潮流向大致为NE向,为周期性往复流.其中,涨潮潮流历时约为6.1 h,落潮潮流历时约为6.4 h,落潮潮流历时大于涨潮潮流.流速平面分布上,流速由外海向岸边递减,外海流速约为0.3 m·s-1,近岸流速不足0.05 m·s-1.由于受西侧乐岛、东侧白鹭岛形成的双岬角掩护作用,潮流绕过岬角进入工程海域之后流速明显减小,距离岸边约600 m范围内涨、落急流速均在0.01~0.15 m·s-1范围内. 以夏季典型大潮为例,潜堤建造前后工程海域的流速差值场如图7所示.由图可知,离岸潜堤附近的水体运动方向与离岸潜堤的布置方向平行,潜堤建设后潮流场仅有微小的改变.因此,潜堤不会减小掩护区海域内的水体交换能力,对海域环境没有负面影响,保证了旅游海滩海域水质. a 大潮涨急 b 大潮落急 c 小潮涨急 d 小潮落急图6 工程前大小潮涨、落急时刻流速场Fig.6 Depth-averaged velocity distribution at the moment of maximum flood and ebb of spring and neap tide before the project a 涨急 b 落急图7 工程前后的涨、落急时刻流速差值场(工程后减工程前)Fig.7 Current velocity changes induced by offshore submerged breakwaters 利用经过验证的波流耦合模型,分别计算了平均海平面下常浪(波高0.62 m)和强浪(波高1.50 m)下的波浪场,在此基础上研究工程对波浪的影响. 图8为常浪和强浪下潜堤建成前后波高差值分布.由图可知,常浪下,潜堤对其背后区域具有一定的掩护作用,波浪通过潜堤后发生波能损耗使波高略微减小,在离岸潜堤后方100 m范围内的波高削减程度约为0.05 m;强浪下,潜堤对波浪的削减作用较强,波浪通过潜堤后波高明显减小,但同时由于波高增大,波浪的绕射现象也变得更为明显,使得离岸潜堤对较远的近岸区域的波浪削减作用较小,在离岸潜堤后方约100 m范围内对强浪的波高削减度达0.2~0.4 m,往近岸方向潜堤对波高的削减作用越来越小. a 常浪 b 强浪图8 常浪和强浪下潜堤建成前后波高差值分布(工程后减工程前)Fig.8 Normal and strong wave height changes induced by offshore submerged breakwaters 为了统计分析潜堤掩护区不同区域的波高变化情况,根据波流耦合模型,在潜堤掩护区内布置了30个波浪监测站点,分为A和B两个区域,分别位于两个潜堤的波影区,见图9.图10为工程前后波浪监测站点处的波高直方图.由图10可知,常浪下,A区东侧区域几乎不受影响,A区西侧岸边区域受养滩工程影响波高减小了0.3 m,在潜堤掩护区波高的减小均约为0.05 m;B区岸边区域波高减小了0.3~0.4 m,在潜堤掩护区的减小幅度大于A区,为0.03~0.08 m.而在强浪下,在A区域A15测站距离潜堤最近,波高减幅达0.38 m;在B区域B11测站位于潜堤掩护区,波高减幅达0.22 m.因此,潜堤掩护区在常浪下总体的减小幅度约为10%,在强浪下总体的减小幅度约为20%. 图9 波浪监测站点分布Fig.9 Positions of wave observation points a A区域常浪 b A区域强浪 c B区域常浪 d B区域强浪图10 工程前后波浪监测站点处的波高对比Fig.10 Comparison of wave height on observation points before and after the project (1) 生态修复工程实施后潮流场仅有微小的改变,离岸潜堤几乎没有减小掩护区海域内的水体交换能力,保持了海域内水动力环境. (2) 对于常浪(入射波高0.62 m),离岸潜堤的存在使其后方100 m内的波高减小约0.05 m,而对于强浪作用(入射波高1.50 m),堤后100 m内波高减小达0.2~0.4 m,离岸潜堤对强浪的防护作用更大,可大大减少风暴天气下的海滩侵蚀. (3) 山海关旅游海滩生态修复工程的建设既保护了工程海域水动力环境,又削弱了波浪特别是强浪对海滩的侵蚀,有利于维持当地旅游海滩的生态环境与稳定.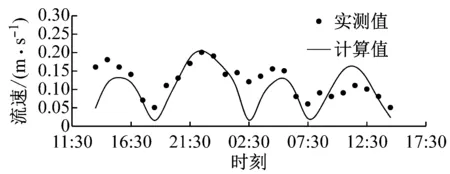


3 计算结果
3.1 潮流

3.2 波浪




4 结论
