双电机耦合驱动系统低速档扭转振动特性分析
2019-01-08朱炳先周广明盖江涛韩政达
朱炳先, 周广明, 盖江涛, 韩政达, 马 田
(中国北方车辆研究所 车辆传动重点实验室, 北京 100072)
混合动力车辆动力传动系统采用行星齿轮传动技术能很好地解决多个动力源的耦合问题. 对于某采用双电机耦合驱动方式的履带车辆, 行星齿轮传动系统具有功率分/汇流能力强、 结构紧凑、 传动比大、 承载能力大等优点[1], 可以有效满足传动能力、 空间布局等方面的需求. 但由于行星齿轮传动系统的复杂性, 大量行星齿轮排的加入给该双输入-双输出传动系统带来了一系列振动问题, 从而对传动系统的传递效率和使用寿命造成负面影响, 对于整车的动力、 传动系统的各个轴、 杆、 齿轮部件的使用寿命和可靠性都有极大的损害[2]. 同时, 在以电动机为主要动力源的双电机耦合驱动系统中, 由于电动机系统的振动激励频率与行星传动系统固有频率相接近, 会在传动系统产生新的系统共振问题[3]. 薛玉春[4]的研究表明, 复杂和显著的耦合振动会对驱动电机转子和定子的碰摩失效产生较大的影响, 增大轴承的失效率, 影响电机的可靠性, 加剧轴承的磨损与松动, 缩短轴承的使用寿命, 影响整个传动系统的可靠性. 另外, 动力传动系统的振动会对车载电池的基本性能、 安全性、 可靠性和耐久性产生很大的负面影响[5]. 因此, 对文献[6]提出的一种双电机耦合驱动系统的扭转振动固有特性进行研究非常必要且有实际价值.
双电机耦合驱动系统是典型的双输入-双输出系统, 其系统结构如图 1 所示[7], 主要由左右两侧驱动电机和耦合机构组成.

图 1 双电机耦合驱动系统结构图Fig.1 Structure diagram of double motor coupling drive system
本文以双电机耦合驱动系统为研究对象, 利用行星传动系统的纯扭转动力学模型[8-10], 以低速档为例, 建立了双电机耦合驱动系统的整体纯扭转动力学模型, 并对其固有特性、 连接轴支承刚度对系统固有特性的影响进行了分析.
1 双电机耦合驱动系统建模
1.1 行星排纯扭转动力学模型
假设行星轮圆柱齿轮按照标准中心矩安装且沿行星架均匀分布, 惯性参数和支撑刚度都相同, 忽略其陀螺效应和向心力的影响; 忽略齿轮啮合的静传递误差以及啮合刚度的时变性, 采用啮合刚度的平均值即综合啮合刚度, 假设所有啮合齿轮的综合啮合刚度及啮合角都相等且为常数; 不考虑齿侧间隙[11], 有如图 2 所示的行星排纯扭转模型.

图 2 行星排纯扭转动力学模型Fig.2 Pure torsional dynamic model of planetary
图 2 中,c,r,s分别表示行星架、 齿圈、 太阳轮;kju(j=c,r,s)为第j个构件的回转支承刚度;uj(j=c,r,s,1,2,…,N)为系杆、 齿圈、 太阳轮及各行星轮的扭转位移;krn,ksn分别为第n个行星轮与齿圈及太阳轮的内外综合啮合刚度,crn,csn分别为第n个行星轮与齿圈及太阳轮的内外啮合阻尼,Ψn为第n个行星轮的初相位.
根据牛顿力学定律即可列出如下所示各构件扭转振动微分方程.
行星架
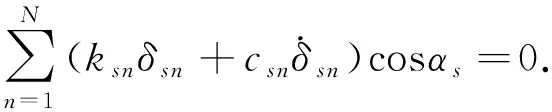
齿圈
(2)
太阳轮
(3)
行星轮
n=1,2,…,N,(4)

式中:δsn和δrn为太阳轮、 齿圈与第n个行星轮位移沿啮合线方向的分量; 下标p表示行星轮;N为行星轮个数;mp为行星轮质量;αr为内啮合齿轮啮合角;αs为外啮合齿轮啮合角;Ji(i=c,r,s,1,2,…,N)为构件i的转动惯量;rc为行星轮几何形心到系杆距离;rr和rs分别为齿圈、 太阳轮的基圆半径; 各行星轮的基圆半径为ri(i=1,2,…,N).
根据该方法建立的行星排模型, 其啮合刚度矩阵为一个6×6的方阵, 以其中左侧减速排(齿圈固定)为例, 其啮合刚度矩阵Kmlb如下
1.2 双电机耦合驱动系统建模
图 3 是分别以左右两侧电机为起点, 根据动力传递路线对系统进行简化, 得到的动力传递简图.
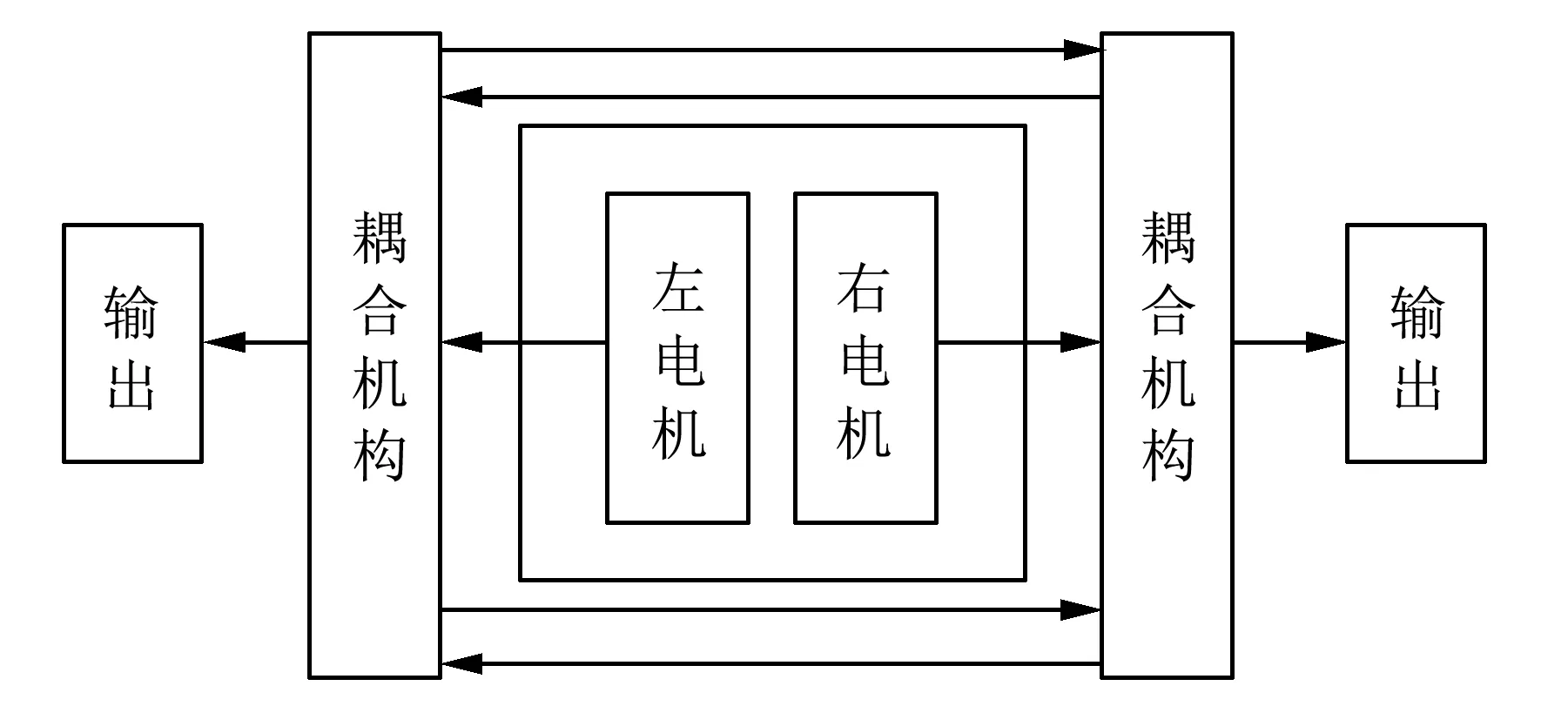
图 3 双电机耦合驱动系统动力传递简图Fig.3 Power transfer diagram of double motor coupling drive system
电机输出的扭矩经减速排传递至耦合机构, 耦合机构分别受到两侧电机输出扭矩影响, 且扭矩具有耦合关系. 整个系统共40个自由度. 根据系统扭振传递简图对双电机耦合驱动系统建立纯扭转动力学模型如下:
右电机
减速排太阳轮
减速排行星轮
n=1,2,3,4.
减速排行星架
耦合排太阳轮
耦合排行星轮
n=1,2,3,4.
耦合排行星架
其中

系统主要建模参数包括: ① 电机转子转动惯量; ② 各太阳轮、 行星轮、 行星架、 齿圈转动惯量; ③ 各行星轮质量; ④ 太阳轮、 行星轮、 齿圈的基圆半径以及行星架的半径; ⑤ 行星轮与太阳轮、 齿圈间的综合啮合刚度及啮合角; ⑥ 连接轴扭转刚度. 其中, 各部件转动惯量、 行星轮质量通过三维模型得到, 连接轴的转动惯量和扭转刚度分别通过式(5)和式(6)计算得到.


基圆半径等于分度圆直径乘以分度圆压力角的余弦值的一半.
当圆柱齿轮按照标准中心距安装时, 行星架半径即为太阳轮和行星轮分度圆之和的一半, 齿轮间啮合角即为分度圆压力角. 由于齿轮啮合重合度的存在, 齿轮间啮合刚度具有时变性, 建模时忽略啮合刚度的时变性, 采用啮合刚度的平均值即综合啮合刚度. 综合齿啮合刚度根据式(7)计算得到, 其中B为齿宽,d为主动轮分度圆直径, 单位m.
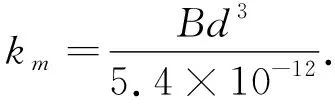
进行固有特性分析时, 令阻尼为零.
建模得到系统的啮合刚度矩阵如K矩阵所示, 可知该矩阵所表达的机械结构啮合关系与本文研究对象相匹配.
其中,Kl与Kr,Kl_r与Kr_l互为关于次对角线对称的矩阵,O1为8阶0矩阵,O2为7阶0矩阵.

2 固有特性分析
行星齿轮传动系统的振动形式, 按照固有频率及振型的特点一般划分为系统扭转振动模式和行星轮振动模式两种振动模式[12]. 考虑到所研究机构的特性, 根据获取的固有特性, 将双电机耦合驱动系统的振动模式划分为整体扭转振动模式、 行星轮振动模式和连接轴扭转振动模式.
对前述模型求解特征值和特征向量, 得到系统的固有频率和各节点对应的振幅. 将振幅结果归一化、 排序后得到下列振型图(如图 4~图 6 所示, 横坐标为节点编号, 纵坐标位相对振幅). 其中, 第1~9阶和第22~25阶振型为系统整体扭转振动模式, 各个行星排各自的行星轮振动状态相同, 如图 4 所示.
可以看出, 左右两侧位置对称的节点具有非常接近的固有频率, 体现了系统的对称性. 同时, 各节点振动时, 其对称位置的节点亦存在与之相应的、 振幅不同的耦合振动. 即振动特性上具有不完全对称性.
第10~15阶、 第16~21阶和第26~31阶振型分别为变速排、 耦合排和减速排的行星轮振动, 其固有频率分别为545.097 7 Hz, 703.838 1 Hz和791.786 1 Hz. 如图 5 所示.
由图 5 可以看出, 这些频率下, 除了各阶固有频率所对应的行星轮以外, 其他构件都没有相对振动, 且振型中的各节点分量的代数和为零, 符合行星轮扭转振动模式的特征. 同时, 固有频率由低到高的排列顺序为: 减速排行星轮>耦合排行星轮>变速排行星轮, 这与各排行星轮之间质量、 转动惯量的关系吻合.

图 4 整体扭转振动模式振型图Fig.4 Vibration situation map of overall torsional vibration mode

图 5 行星轮扭转振动模式振型图Fig.5 Vibration situation map of planetary torsional vibration mode
第32~39阶振型分别为耦合排到变速排连接轴(K3=6.950 9×104N·m·rad-1)、 电机转子到减速排太阳轮(K1=4.772 6×105N·m·rad-1)、 减速排行星架到耦合排太阳轮(K2=1.993 9×106N·m·rad-1)、 变速排行星架到输出端(K4=1010N·m·rad-1)的连接轴扭转振动, 如图 6 所示.

图 6 连接轴扭转振动模式振型图Fig.6 Vibration situation map of connecting shaft torsional vibration mode
由图 6 可知, 刚度较小的连接轴的扭转振动对与之相连的构件影响较大.
在电传动系统中, 永磁同步电机由于气隙磁场非正弦分布以及供电电流不同阶次谐波等因素影响, 输出转矩存在波动. 在本文研究的双电机耦合驱动系统中, 转矩波动频率主要为1阶, 2阶, 6阶频率, 频率的计算公式为f=p×n/60, 其中,p=8为电机的极对数,n为电机转速, 则转矩波动频率分别为f1=2n/15,f2=4n/15和f6=4n/5.
根据双电机耦合驱动系统的固有频率, 结合系统传动比、 主动轮直径, 计算得到与固有频率相对应的电机转速和车速, 其中, 电机最大转速为9 000 r/min.
由于双电机耦合驱动系统具有不完全的对称性, 将分别与左右电机转速相对应的频率统一考虑, 得到如图 7 所示的电机转速与固有频率的对应关系.

图 7 共振转速点示意图Fig.7 Resonance speed point diagram
其中各交点对应的电机转速如表 1 所示.

表 1 共振转速表

表 2 共振车速表
将表 1 中的转速整合, 取主动轮半径为0.313 m, 计算得到对应的车速, 可以看出, 双电机耦合驱动系统在车速0~1.01 km·h-1, 1.59~3.03 km·h-1, 3.92~3.95 km·h-1, 4.71~5.27 km·h-1, 6.07 km·h-1, 7.42~7.53 km·h-1, 8.05~8.10 km·h-1, 9.51~9.55 km·h-1, 11.76~12.25 km·h-1, 14.84~15.06 km·h-1, 15.82~16.20 km·h-1和23.51~23.52 km·h-1等速度区间中会经历共振点. 如表 2 所示.
3 刚度对固有特性的影响
各行星排之间连接轴的扭转刚度对于双电机耦合驱动系统固有特性的影响是本文的研究重点之一.
K1,K2,K3,K4分别表示电机转子到减速排、 减速排到耦合排、 耦合排到变速排和变速排到输出端连接轴的扭转支承刚度.
在原始值状态下, 各连接轴的扭转刚度取值:K1=4.772 6×105,K2=1.993 9×106,K3=6.950 9×104,K4=1010, 单位N·m·rad-1. 取若干不同的刚度值进行计算, 得到系统的固有频率变化情况如表 3 所示.

表 3 固有频率变化情况表
根据表中数据及振型图分析可以发现, 连接轴取不同刚度时, 各重根数值不变, 表明行星轮振动模式的固有频率仅与啮合刚度及行星轮转动惯量有关, 与行星排间连接轴刚度无关. 同时, 改变连接轴刚度只会对其本身和其左右行星排的固有特性产生影响, 对于未与之直接连接的行星排、 轴的固有特性影响可以忽略不计. 刚度减小会导致连接轴本身及与该轴相连接的行星排整体扭转振动的固有频率变小, 轴本身的振幅会降低, 但其两端连接的行星排的整体扭转振动振幅会增大. 增大连接轴刚度可降低轴两端连接行星排整体扭转振动的振幅, 轴本身的固有频率会随之增大, 轴两端连接的行星排整体扭转振动的固有频率几乎不受影响. 同时, 与该类增大后的高频振动对应的电机转速远远超出了系统工作转速.
4 结 论
以某双电机耦合驱动系统为研究对象, 推导建立了系统的整体纯扭转动力学模型. 利用相关参数对系统进行了固有特性分析, 将系统振动形式划分为整体扭转振动、 连接轴扭转振动和行星轮扭转振动三种模式并进行了分析, 得到如下结论:
1) 对双电机耦合驱动系统整体扭转振动模式和轴系扭转振动模式下振型的分析表明, 系统左右两侧相对应的节点存在振幅不等的耦合振动.
2) 获得了与系统固有频率相对应的电机转速和车速. 车辆在0~25 km·h-1范围内工况下会经历全部共振点, 在实际行驶过程中应尽量避开0~1.01 km·h-1, 1.59~3.03 km·h-1, 3.92~3.95 km·h-1, 4.71~5.27 km·h-1, 6.07 km·h-1, 7.42~7.53 km·h-1, 8.05~8.10 km·h-1, 9.51~9.55 km·h-1, 11.76~12.25 km·h-1, 14.84~15.06 km·h-1, 15.82~16.20 km·h-1和23.51~23.52 km·h-1等速度区间, 以缩短共振时长, 减少共振对系统带来的损害.
3) 通过分析不同连接轴刚度下系统的固有特性, 研究了连接轴刚度与其固有频率、 振幅的相关性以及对其他节点固有特性的影响. 根据相关结论, 可以通过增大行星排之间连接轴的刚度来改善系统的振动特性.
建立的双电机耦合驱动系统纯扭转动力学模型为针对该系统的扭振抑制控制的设计提供了有效的参考模型; 通过分析双电机耦合驱动系统的固有特性, 为扭振抑制控制系统的设计提供了准确输入, 为双电机耦合驱动系统扭振抑制控制方法的研究奠定了基础.
