基于模糊逻辑并联混合动力汽车控制策略研究

张志文， 张 硕， 李天宇

(1. 中北大学 能源与动力工程学院， 山西 太原 030051； 2. 重庆大学 汽车工程学院， 重庆 400044；3. 吉林大学 机械科学与工程学院， 吉林 长春 130022)

0 引 言

截至2017年年底， 我国机动车辆保有量已达3.10亿辆， 年燃油需求量大于2.53亿吨， 机动车产生的尾气排放量高达5 002.3万吨， 我国汽车的排放已经成为最大的污染源， 汽车尾气污染物是形成雾霾、 大气污染及温室效应的主要原因， 对人们赖以生存的环境产生了恶劣的影响[1-2]. 在能源危机和环境污染的双重压力下， 清洁能源汽车的研究成为当下紧要的任务.

纯电动汽车理论上可以实现零排放， 但其推广仍受能源结构、 续驶里程、 快速充电、 电池循环寿命、 安全性、 价格等因素的制约[3]. 混合动力汽车(HEV)由于结合传统汽车与纯电动汽车两者的优点， 是目前良好的过渡产品， 通过不同能源的优化互补， 有效地缓解了纯电动汽车的技术瓶颈[4]. 并联式HEV结构简单， 便于改装， 有效降低汽车自重和制造成本， 发展前景非常广阔.

并联式HEV的工作模式复杂， 对控制策略提出更高的要求[5-6]. 常见的能量管理策略主要包括两大类：机械式自动控制策略与思维式智能控制策略， 前者控制思路清晰， 结构简单， 工作可靠， 应用广泛， 但由于其门限参数是相对固定的， 很难满足所有动态工况的变化， 无法保证整车的最优工作效率与最佳燃油经济性. 全局优化控制与模糊逻辑控制是混合动力汽车常用的智能控制策略， 全局优化控制思路能够实现最优化控制， 但是需要对工况预知[7-9]， 适合于试验台测试、 控制策略评价等领域. 模糊逻辑控制策略能够提高系统的鲁棒性， 适合于解决非线性系统的控制问题[10].

Vural 等人于2014年采用遗传算法建立隶属度函数和模糊集， 实现混合动力系统转矩分配[11]； Moghbeli 等人于2014提出了一种基于动态规划模糊能量管理策略来解决混合动力系统能量分配的问题[12]； Mustafa 等人于2015年基于双模糊控制器控制电机与电池的工作模式. 由于模糊控制还不能实现全局最优控制[13]， 很多科研工作者运用遗传算法、 粒子群算法、 二次规划等优化算法对控制策略进行优化. ABDELSALAM 等[14]以车速、 驱动力矩、 电池SOC等参数建立优化模型， 寻求全局最优解， 并验证了其有效性. 本文结合并联式HEV自身特点， 采用模糊逻辑研究其智能控制策略， 通过在线实时感知负载载荷大小与动力电池的SOC值， 控制发动机工作点与电机转矩， 实现节能减排.

1 HEV系统结构及工作模式

1.1 并联式HEV动力系统结构

并联式HEV的系统结构主要包括：发动机、 电机、 动力电池、 传动系统等. 发动机与电机有多种组合方式， 选择双轴转矩耦合式结构方案， 图 1 为系统结构框图.

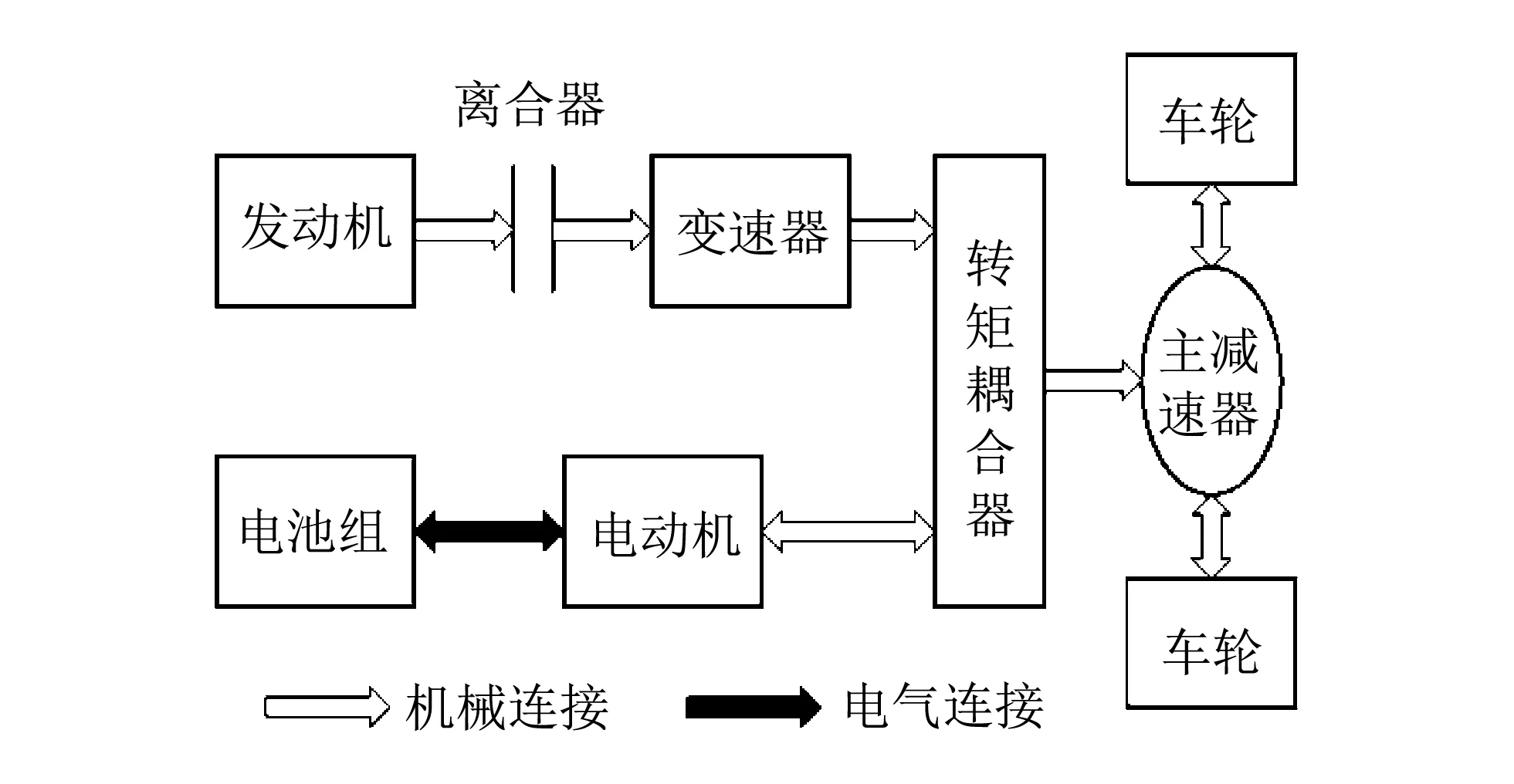
图 1 并联式HEV动力系统结构框图Fig.1 Power system structure diagram of the parallel HEV(hybrid electric vehicle)

转矩耦合器将发动机与电机输出的扭矩进行分配， 实现系统不同的工作模式. 发动机通过离合器将动力输入变速器系统中， 输出的动力直接驱动行走系统， 或者将多余的能量通过转矩耦合器供电动机发电， 将电能储存到动力电池中； 电机单独驱动行走系统， 或者与发动机共同驱动行走系统； 制动过程通过控制转矩耦合器与电动机的工作模式实现能量回收， 将回收的电能储存到电池组中.

1.2 并联式HEV的工作模式

根据并联式HEV动力系统结构特点分析其工作模式， 主要包括发动机单独驱动、 电动机单独驱动、 复合驱动和再生制动能量回收四种模式[7,15]. 车辆在轻载、 起步、 低速等工况下， 动力电池SOC值较高， 为了提高能源利用率， 一般采用电机单独驱动模式； 随着车速逐渐升高或者在重载工况下， 负载需求功率偏大， 一般采用发动机单独驱动模式； 在急加速、 爬陡坡等大负荷工况下， 车辆采用发动机和电动机复合驱动模式； 车辆在制动过程时， 控制器将电动机切换成发电机模式进行制动能量回收， 将回收的电能储存到动力电池中.

2 整车模型的建立

2.1 整车动力学模型建立

汽车在运行过程中， 驱动力与助力构成力平衡模型. 根据模型受力分析， 阻力主要包括加速度阻力、 滚动阻力、 空气阻力和爬坡阻力. 采用经验模型将汽车结构进行简化， 将整车简化为一个质量模块来分析汽车的整车模型[16]， 受力分析如图 2 所示.

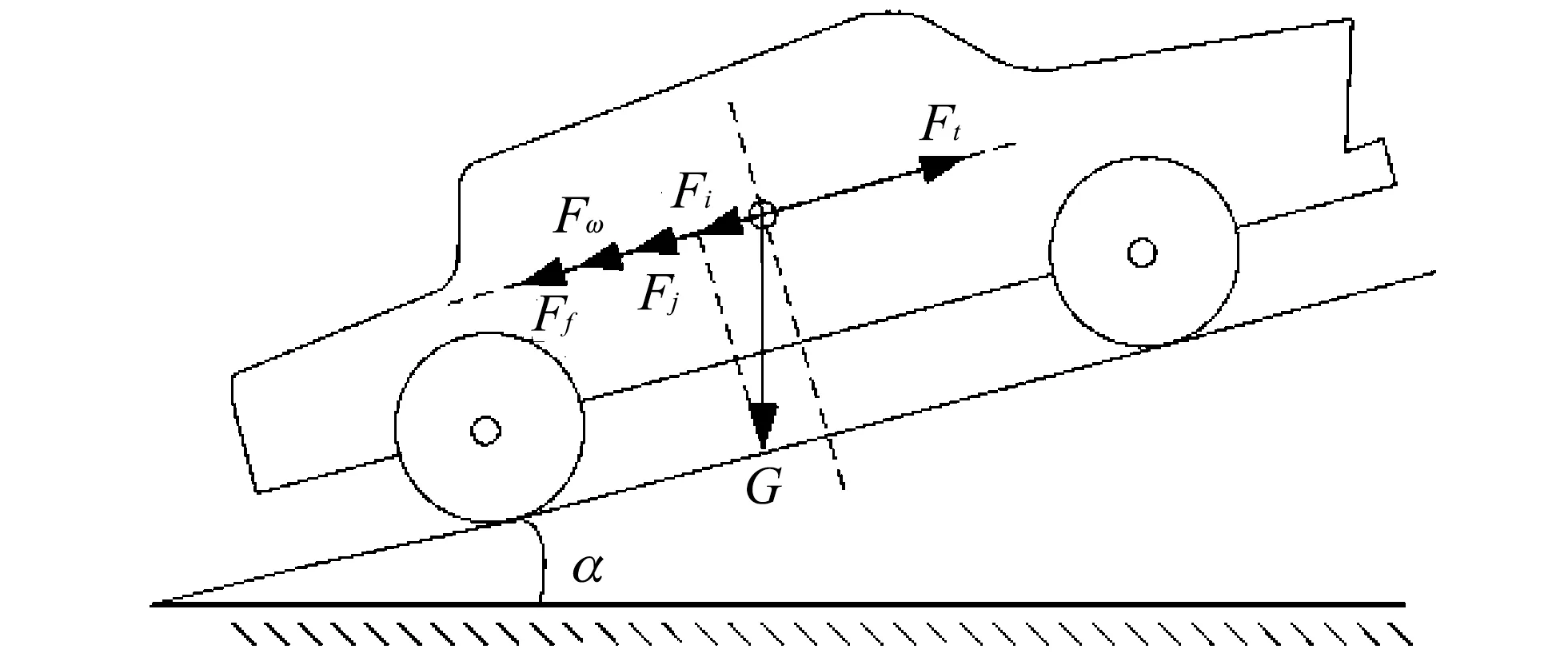
图 2 整车受力分析图Fig.2 Analysis diagram of the force for the vehicle

根据牛顿第二定律， 列出平衡方程式

Ft=Ff+Fw+Fi+Fj,(1)

式中：Ft为驱动力；Ff为滚动阻力；Fw为空气阻力；Fi为坡度阻力；Fj为加速度阻力.

将式(1)进行分解， 整车动力学方程[17]为

(2)

式中：Ttq为动力系统输出的总扭矩；ig为变速箱对应档位传动比；i0为主减速传动比；ηT为传动系统的总效率；r为对应车轮半径；G为汽车总重 力；f为整车滚动阻力系数；CD为对应的空气阻力系数；A为整车的迎风面积；u为汽车与空气的相对速度；i为对应的坡度；δ为汽车质量换算系数；m为汽车总质量； du/dt为整车加速度.

推导出汽车在改定车速的情况下动力系统需要提供的扭矩为

(3)

在仿真软件中， 以循环工况已知参数作为输入变量， 根据整车动力学方程建立传动系统动力学模型， 实现系统仿真过程.

2.2 车辆主要参数

以某小型轿车为设计原型， 设计并联式HEV满足其所有性能需求， 主要参数如表 1 所示.

表 1 车辆主要仿真参数

2.3 整车模型的建立

根据所研究的并联式HEV动力系统结构， 基于MATLAB/Simulink平台， 利用ADVISOR 软件搭建整车仿真模型[18]， 如图 3 所示.

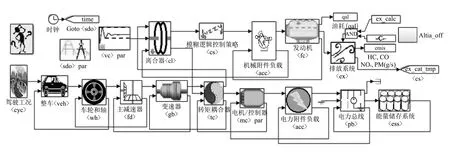
图 3 并联式HEV整车仿真模型Fig.3 Simulation model of the parallel hybrid electric vehicle

3 整车模糊逻辑控制策略

3.1 控制目标

模糊逻辑控制策略的目标是：在保证系统正常工作的前提下， 动力电池SOC值达到动态平衡并实现整车最佳燃油性. 要求发动机平稳工作在燃油效率较高和经济性较好区域， 在一定工况下， SOC值的变化在设定范围内， 以延长电池使用寿命长、 提高充放电效率. 确定发动机最佳工作区域有两种控制模式：一种是基于燃油消耗的控制模式， 根据发动机万有特性图， 计算瞬时油耗并以此限制其工作点； 另一种是基于效率的控制模式， 控制发动机工作在其峰值效率区域内. 采用第二种控制模式， 在满足工况转矩要求的前提下寻求HEV的最小发动机装机功率与最佳燃油区域.

3.2 模糊控制原理

通过模糊推理系统(FIS)来解决汽车行驶过程中高度非线性和时变特性的问题. 将动力电池的SOC值作为FIS的第一个输入量， 将动力总成需求扭矩Treq作为FIS第二个输入量， 将发动机转矩作为输出量. 为了实现模糊推理系统的通用性， 变量在输入模糊推理系统之前， 将输入变量量化到通用论域内， 由模糊推理系统经过模糊化、 模糊推理、 去模糊化等过程输出发动机转矩参量， 通过输出变量还原系统工作模式， 得到发动机转矩， 根据整车负载需求转矩计算电动机工作转矩， 图 4 为原理图.

图 4 模糊控制能量管理策略原理图Fig.4 Schematic diagram of fuzzy control energy management strategy

电动机转矩可以用式(4)来确定[11]

TEM=Tload-Tout,(4)

式中：Tload为动力总成需求扭矩；Tout为发动机需求转矩.

3.3 变量论域的确定

3.3.1 输入变量论域

动力总成需求转矩Treq的论域确定为[0，Tmax]， 当Treq>Tmax时， 控制发动机工作于最大转矩曲线上， 当Treq=0时， 发动机给电池充电或关闭. 现将论域[0，Tmax]量化到通用论域[1,7]， “1”表示最小转矩， “4”表示最大效率曲线所对应的转矩Ttarget， “7”表示最大转矩. 图 5 是Geo 1.0 L (41 kW) SI型发动机万有曲线图， 根据图 5 绘制出发动机最大转矩曲线和最大效率曲线如图 6.

图 5 发动机万有特性曲线图Fig.5 Universal characteristics curve of engine

图 6 发动机最大转矩曲线和最大效率曲线图Fig.6 Maximum torque curve and maximum efficiency curve of the engine

基于图 6 制定输入变量量化原则：

当输入变量Treq≤Ttarget时，Treq论域为[1，4]， 将[0，Ttarget]用式(5)量化到区间[1，4].

(5)

当输入变量Treq>Ttarget时， 论域为[4,7]， 将[Ttarget,Tmax]用式(6)量化到区间[4,7].

(6)

输入变量SOC的论域为[0,1]， 为了控制方便， 用式(7)量化到区间[1,7]：

(7)

式中：u为实际输入的SOC值；SOChigh为设定上限SOC值；SOClow为设定下限SOC值.

根据上述论域制定原则， 建立输入变量量化系统Simulink模型如图 7 所示.

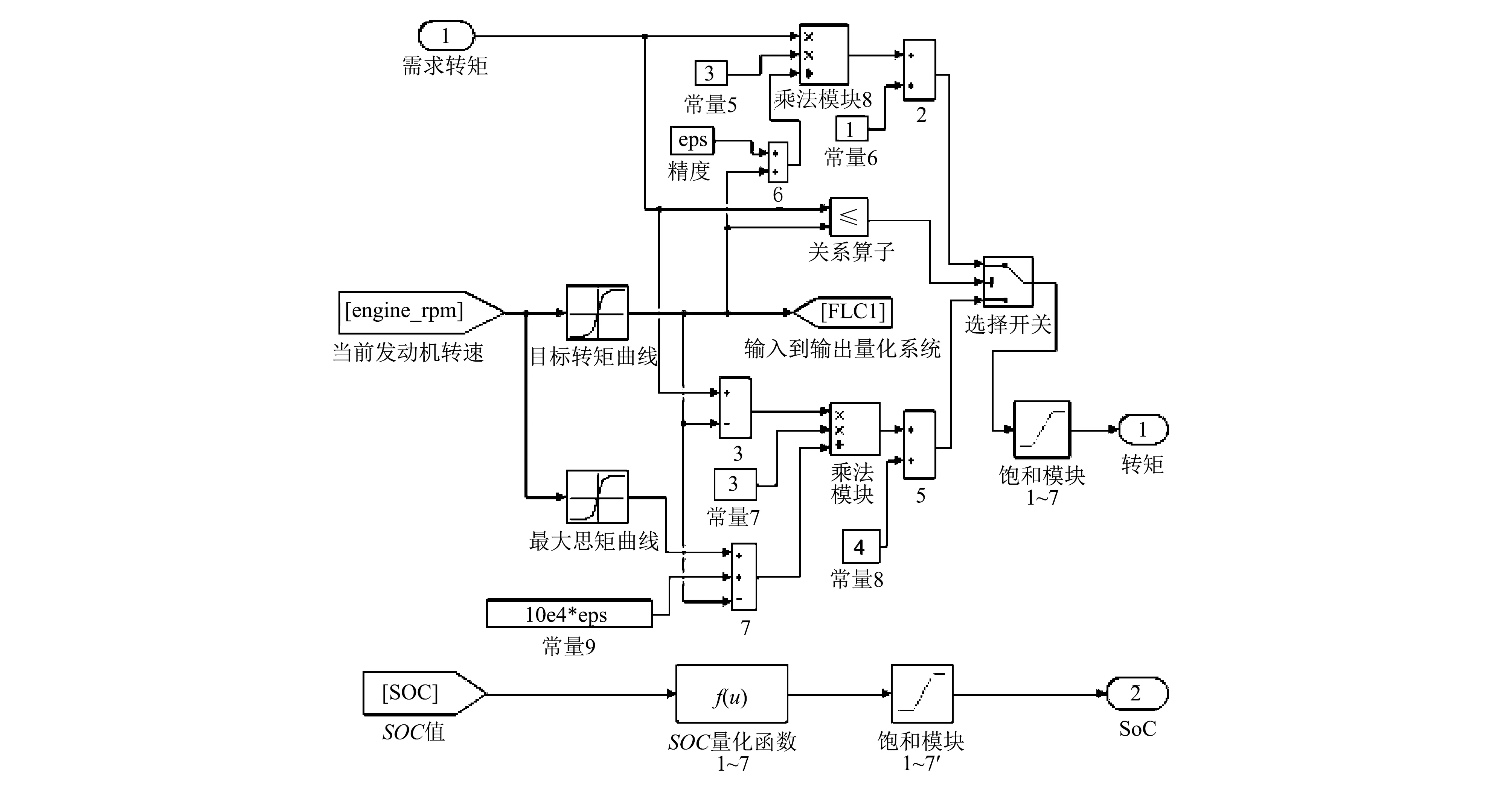
图 7 输入变量量化系统的Simulink模型Fig.7 Simulink model of the input variable quantization system

3.3.2 输出变量论域

发动机工作转矩Tout是模糊逻辑控制器的输出变量， 其论域区间为[1,7]， 精确化发动机需求转矩的过程如下.

(8)

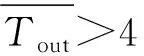
(9)

输出变量还原系统Simulink模型如图 8 所示.

图 8 输出参数还原系统Simulink模型Fig.8 Simulink model of the output parameters restoration system

3.4 控制变量模糊子集的确定

表 2 和表 3 是根据变量论域确定变量模糊参量的过程.

确定控制变量的模糊子集， 输入变量Treq和输出变量Tout的模糊子集为{VS，SE，S，M，B，BE，VB}； 电池SOC的模糊子集为{very low，lower，low，normal，high，higher，very high}.

表2输入变量Treq和输出变量Tout模糊参量

Tab.2Fuzzy parameter ofTreqandTout

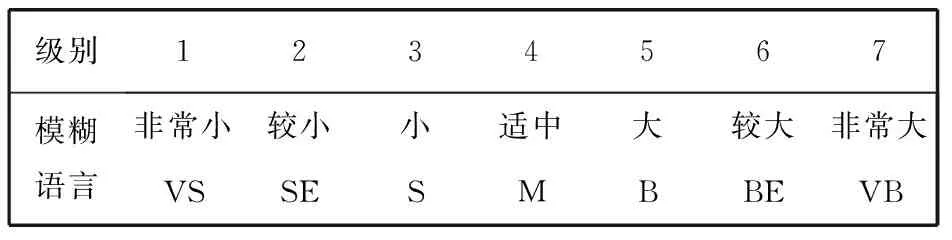
级别1234567模糊语言非常小较小小适中大较大非常大VSSESMBBEVB

表3动力电池SOC的模糊参量

Tab.3Fuzzy parameter ofSOC

级别1234567模糊语言非常低较低低适中高较高非常高very lowlowerlownormalhighhighervery high

3.5 控制变量的隶属函数设计

隶属度函数的形状决定了控制器的灵敏度， 输入变量和输出变量均采用较为典型的三角形隶属函数， 输入变量Treq和输出变量Tout隶属函数曲线如图 9 所示， 图 10 为动力电池SOC值的隶属函数曲线.

图 9 输入变量Treq和输出变量Tout隶属函数曲线Fig.9 Membership function curve of Treq and Tout

图 10 输入变量SOC的隶属函数曲线Fig.10 Membership function curve of SOC

3.6 模糊逻辑控制规则设计

图 11 为模糊逻辑控制流程图， 在进行模糊逻辑控制过程中， 将动力电池的SOC值设置为第一参考量， 当动力电池的SOC很高时， 且负载需求扭矩不是非常大， 发动机不工作， 汽车处于纯电动工作状态； 当动力电池的SOC值在适中状态时， 汽车需求扭矩较大， 控制策略模块输出较大的需求扭矩， 汽车处于发动机和电动机联合驱动状态； 当动力电池SOC小于某阈值时(设定为0.5)， 为保证充放电性能和使用寿命， 电池将进入休眠或者充电状态.

图 11 模糊逻辑控制流程图Fig.11 Flow chart of the fuzzy logic control strategy

根据上述控制方案制定的模糊逻辑控制规则如表 4 所示.

制定出模糊规则之后， 经过模糊推理器得出模糊输出量， 使用Mamdani模糊推理方法计算输出结果， 然后采用重心法进行反模糊化， 得到精确控制量对控制对象进行控制.

表 4 模糊逻辑控制规则表

3.7 模糊逻辑控制策略Simulink建模

基于MATLAB模糊逻辑工具箱设计模糊推理系统， 如图 12 所示， 通过MATLAB/Simulink对模糊逻辑控制策略建模.

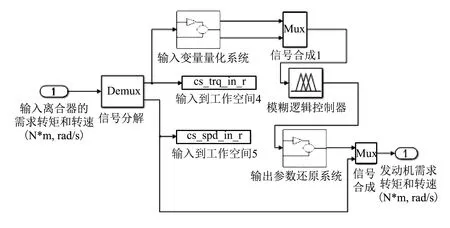
图 12 模糊逻辑控制策略Simulink模型Fig.12 Simulink model of the fuzzy logic control strategy

4 控制策略仿真结果及分析

4.1 行驶工况的选择

本文所研究并联混合动力汽车主要针对的是城市路况， 选择美国工况标准中的UDDS行驶工况进行整车的仿真实验[19]. 图 13 所示为曲线图， 工况循环持续的时间是1 369 s， 行驶路程11.99 km， 最高车速91.25 km/h， 平均车速31.51 km/h， 停歇时间259 s， 停车次数为17次.

利用ADVISOR二次开发将控制策略嵌入整车模型中进行仿真实验[20]. 为验证模糊逻辑控制策略的优越性， 在UDDS道路循环工况下进行对比仿真实验， 分别对模糊控制和逻辑门限能量管理策略进行仿真. 设定电池初始SOC值为0.8， 最低SOC值为0.5， 选择0～100 km/h加速所用时间、 最高加速度、 最高车速等参数作为车辆动力性能输出结果.

图 13 UDDS工况循环图Fig.13 Diagram of UDDS operating cycle

4.2 发动机工作效率对比分析

图 14 为两种控制策略下发动机工作点的分布图. 通过对比发现， 模糊逻辑控制策略下的发动机工作点分布较为集中， 且主要集中在最大效率转矩曲线附近， 而逻辑门限能量管理策略下的发动机工作点分布相对分散， 通过计算：模糊逻辑控制策略下的发动机工作效率为26.50%， 逻辑门限能量管理策略下的发动机工作效率为25.66%， 模糊逻辑控制策略在一定程度上提高了发动机的工作效率.

×—模糊逻辑能量管理策略控制下的发动机工作点； ○—逻辑门限能量管理策略控制下的发动机工作点图 14 发动机工作点分布图Fig.14 Engine operating points on efficiency map

4.3 动力电池SOC值变化曲线对比分析

图 15 与图 16 为两种策略下电池SOC值变化曲线. 从图中可以看出， 两种控制策略都能保证电池的SOC值保持在0.6左右， 且都处于浅循环状态， 证明两种能量管理策略都可以实现了动力电池组动态平衡， 实现了预期设计效果. 图中的变化曲线均出现了波动现象， 原因是在工况循环中， 在路况需求转矩较大， 使得SOC值下降迅速.

图 16 模糊逻辑控制下电池SOC值变化曲线Fig.16 Changing curve of SOC under fuzzy logic control

模糊逻辑能量管理策略控制下的电池SOC值曲线在下降阶段较为平稳. 仿真实验结果表明， 在同一设置范围内， 模糊逻辑控制策略能更好地满足设计要求.

4.4 动力性能及传动系统工作效率对比分析

表 5 为两种控制对比仿真数据结果. 车辆的燃油经济性能与动力性能是两个不可兼得的指标， 模糊逻辑控制下的车辆的动力性能与逻辑门限控制相比有所下降， 但下降程度很小， 模糊逻辑控制策略旨在提高燃油效率和燃油经济性， 动力性能下降符合预期设想. 但是， 对传动系统的总效率而言， 模糊逻辑控制策略优于逻辑门限能量管理策略， 说明模糊逻辑控制策略对提高传动部件的工作效率有一定的作用.

表 5 动力性能及传动系统工作效率仿真结果

4.5 排放性能和燃油经济性对比分析

表 6 为两种控制策略排放性与燃油经济性仿真对比数据， 仿真结果表明逻辑门限能量管理策略下车辆百公里油耗为7.15 L， 模糊逻辑控制策略下车辆百公里油耗为6.47 L， 很大程度上改善了车辆的燃油经济性能. 但就排放结果而言， 模糊逻辑控制策略控制下的一氧化碳的排放量明显减少， 但氮氧化合物的排放量减少并不是特别明显， 碳氢化合物的排放量反而有少量的增加.

表 6 排放性能与燃油经济性仿真结果

5 基于多目标的控制策略优化

5.1 优化目标

仿真结果发明， 所设计的模糊逻辑能量管理策略虽然能够有效减少燃油消耗， 但从全局角度考虑， 控制策略还需进一步优化， 同时车辆排放性能的控制结果并不理想， 因此， 还需根据多目标优化的思想对所设计的控制策略进行优化， 在保证发动机工作效率的基础上， 使得废气排放量最小.

5.2 优化思想

典型的多目标问题由一组目标向量、 一组等式约束向量、 一组不等式约束向量以及n维决策变量组成[21-22], 其数学模型描述为

minf(x)=(f1(x),f2(x),…,fm(x))

s.t.gj(x)≤0j=1,2,…,J,

hk(x)=0k=1,2,…,K,(10)

式中：x为n维决策变量;f为m维目标向量;gj为j维不等式约束向量;hk为k维等式约束向量.

在ADVISOR软件系统中， 各种排放污染物的数值是通过实验测定的， 采用二维插值函数确定各函数之间的关系曲线， 发动机转矩为已知条件， 通过函数关系确定对应的发动机工作效率及各污染物的排放特性.

5.3 优化模型

优化函数用如下公式表示

minf(x)=ηe(x)W0+HC(x)W1+…

…CO(x)W2+NOx(x)W3,

s.t. 0≤x≤Tmax,(11)

式中： 优化函数f(x)是关于发动机转矩的函数，f(x)最小值所对应的转矩就是所求的优化转矩；ηe(x)为发动机工作效率函数；W0为效率权重； HC(x)为碳氢化合物排放函数；W1为碳氢化合物排放权重； CO(x)为一氧化碳排放函数；W2为一氧化碳排放权重； NOx(x)为氮氧化合物排放函数；W3为氮氧化合物排放权重. 各权重的值设计如表 7 所示.

表 7 权重取值表

5.4 优化结果对比

将模糊控制策略优化前后的输出结果进行对比， 结果如表 8 和表 9 所示.

表 8 排放性能与燃油经济性优化结果

表 9 优化后动力性能及传动系统工作效率仿真结果

从表中的数据看出， 与优化前相比， 碳氢化合物的排放量减少了8.2%， 一氧化碳的排放量减少了13.2%， 氮氧化物的排放量减少了4.6%， 燃油消耗也降低了3.1%. 优化后的发动机功率为27.21%， 相对于优化之前提高了2.8%， 反映了发动机的工作效率与排放性能的内在关联性. 优化之后的加速时间有所增加， 但仍能满足行驶需求， 最高车速下降并不明显， 最大加速度和传动系统的工作效率没有发生变化.

6 结 论

基于某型并联式HEV， 在UDDS道路循环条件下对模糊逻辑控制策略进行了模拟仿真， 根据仿真结果得出以下结论：在相同的工况条件下， 与逻辑门限能量管理策略相比， 发动机效率由原来的25.66%提高到26.50%， 油耗减少了0.68 L/100 km， 传动系统的总效率由原来的93.45%提高到了93.75%. 因此， 所研究的模糊逻辑控制策略提高了发动机的工作效率， 在兼顾动力性能的同时， 减少了油耗， 并在一定程度上提高了传动系统的效率， 但在排放性能控制方面效果并不突出， 反映了模糊逻辑能量管理策略不能实现全局最优的不足. 针对这一问题， 基于多目标优化算法对仿真结果进行了进一步的优化， 经过优化之后， HC减少了0.012 g/km， CO减少了0.061 g/km， NOx减少了0.008 g/km， 证明了优化方法的有效性.

由于模糊逻辑控制策略需要大量的实验和经验结果为基础来建立隶属函数， 文中设计的控制策略参数只是建立在大量的仿真实验基础上， 因此在一定程度上限制了控制策略优势的发挥.