分裂四元数矩阵实表示的逆矩阵的求法
2019-01-08孔祥强
孔祥强
(菏泽学院 数学与统计学院, 山东 菏泽 274015)
0 引 言
1843年数学家Hamilton首次提出了四元数的概念, 其形式为H={q0+q1i+q2j+q3k}, 且满足i2=j2=k2=-1,ijk=-1,q0,q1,q2,q3∈R. 1849年, James Cockle研究了分裂四元数, 形式为Hs={p0+p1i+p2j+p3k}, 且满足i2=-1,j2=k2=1,ijk=1,ij=-ji=k,jk=-kj=-i,ki=-ik=j,p0,p1,p2,p3∈R.Hs为结合且非交换的四维克利福德代数, 且含有零因子、 幂等元和幂零元[1-2]. 分裂四元数及分裂四元数矩阵在经典力学和量子力学中均有重要应用[3-4]. 文献[5-6]研究了四元数矩阵实表示的性质和应用; 文献[7-9]研究了四元数矩阵的特征值及特征向量问题, 得到一系列成果, 但这些成果仅局限于四元数方面, 对分裂四元数的研究结果并不多. 文献[10]重点研究了复表示意义下的分裂四元数及分裂四元数矩阵, 得到分裂四元数矩阵的逆矩阵. 本文研究实表示意义下分裂四元数矩阵的性质, 得到基于实表示的分裂四元数矩阵的逆矩阵的新求法, 逆矩阵的求得为进一步研究分裂四元数矩阵的行列式问题、 对角化问题、 特征值及特征向量问题提供了重要理论支撑.
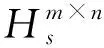
1 分裂四元数矩阵的实表示
设q=q0+q1i+q2j+q3k∈Hs,q0,q1,q2,q3∈R, 定义q的实表示为
⊆R4×4;
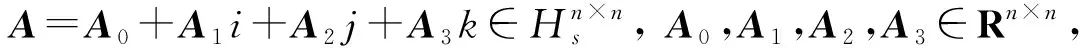
⊆R4n×4n.
由文献[11]易得
定理1
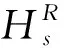
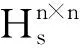
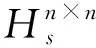
2 分裂四元数矩阵实表示的性质
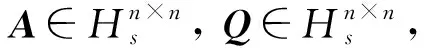
2) (A+Q)R=AR+QR;
3) (AQ)R=ARQR;
4) (AR)-1=(A-1)R.
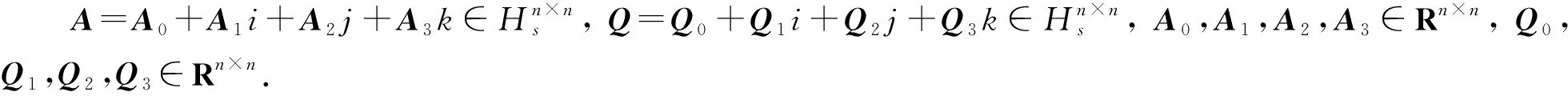
1) 取A=In, 由实表示定义
2) 由实表示定义及矩阵的加法易验证(A+Q)R=AR+QR显然成立.
3)
AQ=(A0+A1i+A2j+A3k)(Q0+Q1i+Q2j+Q3k)=(A0Q0-A1Q1+A2Q2+A3Q3)+(A0Q1+A1Q0-A2Q3+A3Q2)i+(A0Q2-A1Q3+A2Q0+A3Q1)j+(A0Q3+A1Q2-A2Q1+A3Q0)k,

b11=A0Q0-A1Q1+A2Q2+A3Q3,
b12=A0Q1+A1Q0-A2Q3+A3Q2,
b13=A0Q2-A1Q3+A2Q0+A3Q1,
b14=A0Q3+A1Q2+A2Q1+A3Q0,
b21=-A0Q1-A1Q0+A2Q3-A3Q2,
b22=A0Q0-A1Q1+A2Q2+A3Q3,
b23=-A0Q3-A1Q2+A2Q1-A3Q0,
b24=A0Q2-A1Q3+A2Q0+A3Q1,
b31=A0Q2-A1Q3+A2Q0+A3Q1,
b32=-A0Q3-A1Q2+A2Q1-A3Q0,
b33=A0Q0-A1Q1+A2Q2+A3Q3,
b34=-A0Q1-A1Q0+A2Q3-A3Q2,
b41=A0Q3+A1Q2-A2Q1+A3Q0,
b42=A0Q2-A1Q3+A2Q0+A3Q1,
b43=A0Q1+A1Q0-A2Q3+A3Q2,
b44=A0Q0-A1Q1+A2Q2+A3Q3.
设AQ的实表示形式为
由矩阵实表示的定义验证得
c11=b11,c12=b12,c13=b13,c14=b14,
c21=b21,c22=b22,c23=b23,c24=b24,
c31=b31,c32=b32,c33=b33,c34=b34,
c41=b41,c42=b42,c43=b43,c44=b44.
故(AQ)R=ARQR.
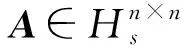
3 分裂四元数矩阵逆矩阵的求法
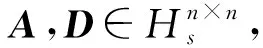
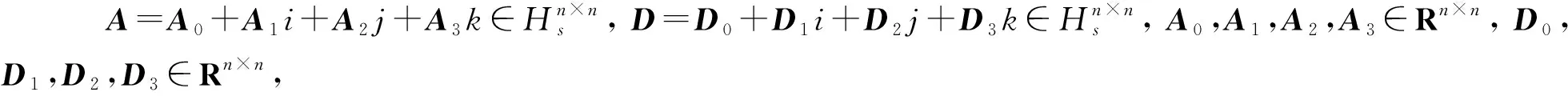
DA=
(D0+D1i+D2j+D3k)(A0+A1i+A2j+A3k)=
(D0A0-D1A1+D2A2+D3A3)+
(D1A0+D0A1+D3A2-D2A3)i+
(D2A0+D3A1+D0A2-D1A3)j+
(D3A0-D2A1+D1A2+D0A3)k.
由DA=In, 则
D0A0-D1A1+D2A2+D3A3=In,
D1A0+D0A1+D3A2-D2A3=0,
D2A0+D3A1+D0A2-D1A3=0,
D3A0-D2A1+D1A2+D0A3=0,
即
由上式可得
则
A0D0-A1D1+A2D2+A3D3=In,
A0D1+A1D0-A2D3+A3D2=0,
A0D2-A1D3+A2D0+A3D1=0,
A0D3+A1D2-A2D1+A3D0=0,
又
AD=(A0+A1i+A2j+A3k)(D0+D1i+D2j+D3k)=
(A0D0-A1D1+A2D2+A3D3)+(A0D1+A1D0-A2D3+A3D2)i+
(A0D2-A1D3+A2D0+A3D1)j+(A0D3+A1D2-A2D1+A3D0)k,
所以AD=In.
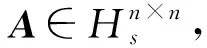
A0,A1,A2,A3∈Rn×n, 则AR可逆的充分必要条件为A可逆.
证明必要性: 由AR可逆,AR∈R4n×4n, 令(AR)-1=TR, 则TRAR=I4n.

则
T11A0-T12A1+T13A2+T14A3=In,
T12A0+T11A1+T14A2-T13A3=0,
T13A0+T14A1+T11A2-T12A3=0,
T14A0-T13A1+T12A2+T11A3=0.
若取T=T11+T12i+T13j+T14k,
其中,T11,T12,T13,T14∈Rn×n,则
TA=(T11A0-T12A1+T13A2+T14A3)+(T12A0+T11A1+T14A2-T13A3)i+
(T13A0+T14A1+T11A2-T12A3)j+(T14A0-T13A1+T12A2+T11A3)k=In.
由命题1知,AT=In, 所以A可逆, 且A-1=T=T11+T12i+T13j+T14k.
定理充分性的证明用上述类似方法可得, 不再赘述. 故AR可逆⟺A可逆.
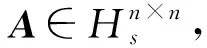
① 写出A的实表示形式AR;
② 求出(AR)-1, 即TR;
③ 取TR中第一行的元素T11,T12,T13,T14(∈Rn×n), 则A-1=T11+T12i+T13j+T14k.
2) 计算A-1的过程可通过计算机编程轻松实现, 避免了冗长繁琐的计算, 节约了时间, 提高了运算效率.
4 算 例
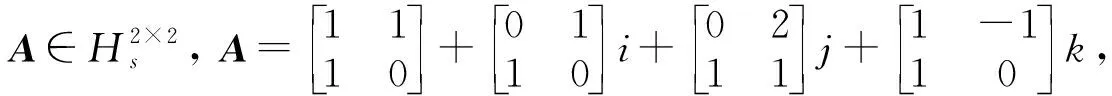
①A的实表示形式为
②
③
则
A-1=T11+T12i+T13j+T14k=



5 结束语
四元数理论和分裂四元数理论是四元数量子力学的重要研究领域. 随着对四元数及四元数矩阵研究的深入, 分裂四元数的研究也逐步引起学者的重视, 并且在对偶分裂四元数及其矩阵方面取得了一定的成果[12-15]. 本文研究了分裂四元数矩阵的实表示, 将分裂四元数矩阵求逆矩阵的问题归结为实数域上矩阵求逆矩阵的问题; 将分裂四元数体上不可交换的问题归结为实数域上可交换的问题. 本文所得求逆矩阵的方法, 大大简化了分裂四元数矩阵的相关运算, 使应用计算机处理相应问题成为可能, 这将对分裂四元数矩阵的进一步研究起到很大的推动作用.
