关于M-矩阵Fan积最小特征值的不等式
2019-01-08牟谷芳
钟 琴, 牟谷芳
(1. 四川大学锦江学院 数学教学部, 四川 彭山 620860; 2. 乐山师范学院 数学与信息科学学院, 四川 乐山 614000)
0 引 言
M-矩阵在矩阵论、 计算数学、 生物学、 物理学、 经济数学等诸多领域有着重要的应用.矩阵的Fan积是特殊的矩阵乘积, 被广泛地应用于概率论中特征函数和偏微分方程中的弱极小原理等方面的研究. 受这些应用背景的影响,并且考虑到两个M-矩阵的Fan积仍为M-矩阵,许多专家和学者致力于M-矩阵Fan积最小特征值下界的研究, 给出了一系列很好的估计式[1-15]. 本文继续该问题的研究, 并且给出M-矩阵Fan积最小特征值下界的新估计式, 该结果计算简单, 精确度更高.
1 预备知识
为方便叙述,引入以下的定义及符号.
记Rm×n(Cm×n)为m×n阶实(复)矩阵的集合,N={1,2,…,n},n≥2.
定义1[1]设矩阵A=(aij)∈Rn×n, 若对于任意i,j∈N, 都有aij≥0, 则称矩阵A为非负矩阵, 记为A≥0.
定义2[1]矩阵A=(aij)∈Cn×n的n个特征值λ1,λ2,…,λn组成的集合称为矩阵A的谱, 记为σ(A), 称ρ(A)=max{|λi|,i∈N}为矩阵A的谱半径.
定义3[1]设Zn×n={A=(aij)∈Rn×n|aij≤0,1≤i,j≤n,i≠j}, 称矩阵A为Z矩阵.
定义4[1]若A=(aij)∈Zn×n且可表示为A=sI-P, 其中P≥0,s≥ρ(P), 则称A为M-矩阵. 特别地, 当时s=ρ(P), 称A为奇异M-矩阵, 当s>ρ(P)时, 称A为非奇异M-矩阵. 记n阶非奇异M-矩阵的集合为Mn.
定义5[1]设A=(aij)∈Zn×n, 记q(A)=min{Re(λ)∶λ∈σ(A)}, 称q(A)为A的按模最小特征值, 简称最小特征值. 由文献[1]知:q(A)∈σ(A).
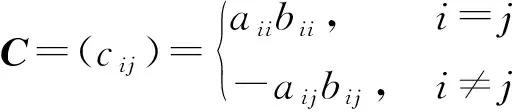
设A∈Mn,B∈Mn, 则A★B∈Mn, 所以M-矩阵的Fan积必有一个最小特征值q(A★B). 关于M-矩阵Fa积最小特征值下界的估计, 文献[1]首先给出了以下经典的结论
q(A★B)≥q(A)q(B).(1)
文献[2-6]分别给出了如下的估计结果
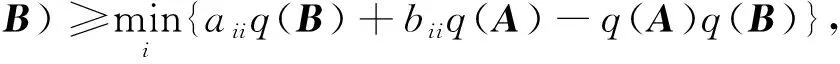
q(A★B)≥
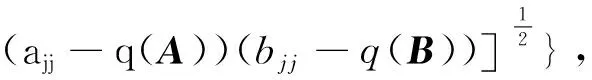

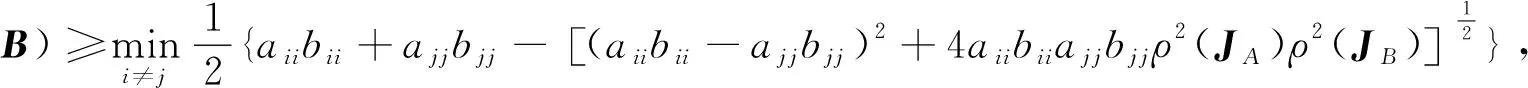

式中:ρ(JA),ρ(JB)是Jacobi迭代矩阵JA和JB的谱半径.
在上述估计式中, 式(1)~(3)需要计算q(A)和q(B), 式(4)~(6)需要计算Jacobi迭代矩阵JA和JB的谱半径, 当矩阵的阶数较高时q(A),q(B)以及ρ(JA)和ρ(JB)难以计算, 所以利用上述不等式来估计q(A★B)的下界难以实现. 本文利用特征值包含域定理, 给出M-矩阵Fan积q(A★B)下界的新估计式, 该估计式只依赖于两个M-矩阵的元素, 计算更简单, 且结果更加接近q(A★B)的真值.
2 M-矩阵Fan积最小特征值的下界
本节给出M-矩阵Fan积最小特征值的下界估计式, 首先给出一些关于特征值包含域的引理和定理.


引理2[5]设A,B∈Mn,D和E是两个正对角矩阵, 则有
D(A★B)E=(DAE)★B=(DA)★(BE)=
(AE)★(DB)=A★(DBE).



其中,
证明当n=1时, 式(7)显然成立, 所以假设n≥2.

D=diag(a-R1(A),a-R2(A),…,a-Rn(A)),
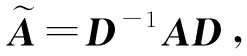
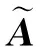

根据引理2可知
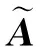
★B=(D-1AD)★B=D-1(A★B)D,

[Λi(A)Λj(A)]α[Λj(AT)Λj(AT)]1-α.
又因为0<λ (aiibii-λ)(ajjbjj-λ)≤[Λi(A)Λj(A)]α[Λi(AT)Λj(AT)]1-α.(8) 解不等式(8)得 也即 其中, 结合定理1和定理2, 得到以下结论: 式中:Λi(A),Λi(AT),Λi(B),Λi(BT)的定义同定理1和定理2. 这里给出一个数值例子用以说明本文结果的优越性. 例考虑M-矩阵A和的Fan积A★B的最小特征值q(A★B), 其中 应用式(1)~(5), 分别得 q(A★B)≥0.191 0,q(A★B)≥1.573 0, q(A★B)≥1.573,q(A★B)≥0.180 8, q(A★B)≥1.523 8. 应用文献[8]定理3.1, 有 q(A★B)≥2.433 3. 应用文献[9]定理3.1和定理3.2, 有 q(A★B)≥2.833 3,q(A★B)≥2.919 9. 应用文献[10]定理2.1, 有 q(A★B)≥2.977 9. 应用文献[11]定理2, 有 q(A★B)≥2.983 2. 应用文献[6]式(6), 有 q(A★B)≥2.983 3. 应用文献[12]定理2, 有 q(A★B)≥2.985 3. 应用文献[13]定理4, 有 q(A★B)≥3. 应用本文定理1(α=0)得 应用本文定理1(α=1)得 应用本文定理2(α=0)得 应用本文定理2(α=1)得 综上, 应用本文定理1和定理2, 将得到M-矩阵A和B的Fan积最小特征值下界的一个最优估计结果q(A★B)≥3.188 5. 实际上, 应用Matlab7.0直接计算得q(A★B)=3.229 6. 从上述例子可以看出本文给出的M-矩阵Fan积最小特征值的下界估计式在一定条件下优于现有的相关结果. 本文给出了M-矩阵Fan积最小特征值的下界估计式, 并且所得估计式仅仅依赖于M-矩阵A和B的元素, 易于计算, 与现有的相关结论相比更接近于q(A★B)的真值.
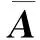
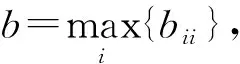
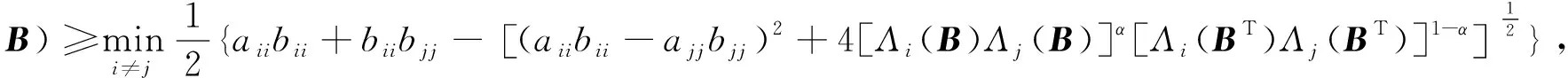
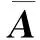


3 数值算例

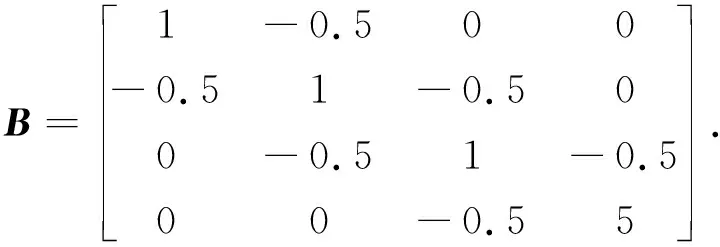
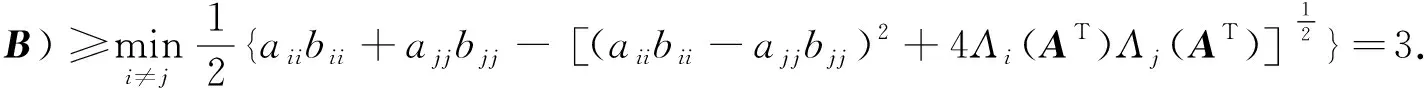





4 结束语
