Existence of Solutions for Fractional Differential Equations Involving Two Riemann-Liouville Fractional Orders

Mohamed Houas

Laboratory FIMA,UDBKM,Khemis Miliana University,Algeria

Abstract.In this work,we study existence and uniqueness of solutions for multi-point boundary value problem of nonlinear fractional differential equations with two fractional derivatives.By using the variety of fixed point theorems,such as Banach's fixed point theorem,Leray-Schauder's nonlinear alternative and Leray-Schauder's degree theory,the existence of solutions is obtained.At the end,some illustrative examples are discussed.

Key Words:Riemann-Liouville integral,existence, fixed point theorem,Leray-Shauders alternative.

1 Introduction

Fractional derivative arises from many physical processes,such as a charge transport in amorphous semiconductors[22],electrochemistry and material science,they are in fact described by differential equations of fractional order[9,10,17,18].Recently,many studies on fractional differential equations,involving different operators such as Riemann-Liouville operators[19,24],Caputo operators[1,3,13,25],Hadamard operators[23]and q-fractional operators[2],have appeared during the past several years.Moreover,by applying different techniques of nonlinear analysis,many authors have obtained results of the existence and uniqueness of solutions for various classes of fractional differential equations,for example,we refer the reader to[3-8,11,12,14,15,19]and the references cited therein.

In this work,we discuss the existence and uniqueness of the solutions for multipoint boundary value problem of nonlinear fractional differential equations with two

Riemann-Liouville fractional orders

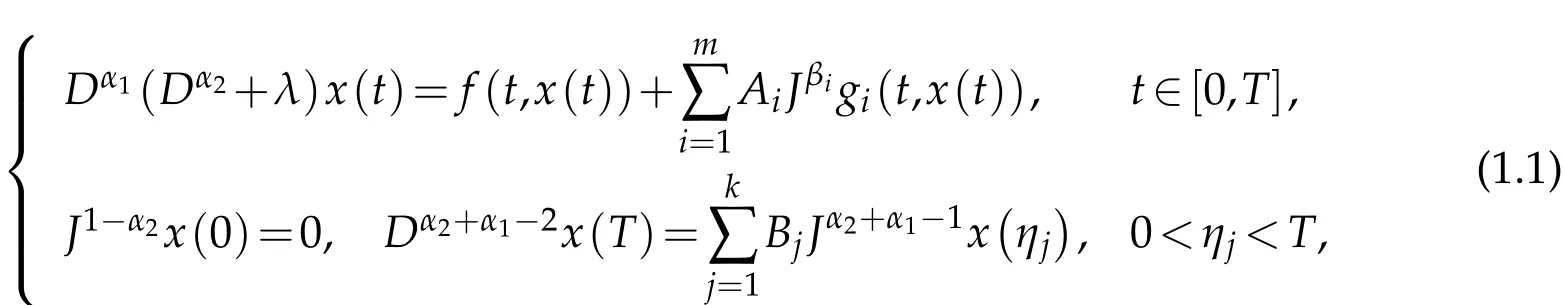
where Dαlis the Riemann-Liouville fractional derivative of order αl,with 0 ＜ αl≤ 1,(l=1,2),1＜ α1+α2≤2,Jϑis the Riemann-Liouville fractional integral of order ϑ ＞0,ϑ∈{βi,1-α2,α2+α1-1},λ,Ai,Bjare real constants and f,gi:[0,T]×R→R,1≤i≤m,1≤j≤k,k≥2 are continuous functions on[0,T].

The existence results for the multi-point boundary value problem(1.1)are based on variety of fixed point theorems,such as Banach's fixed point theorem,Leray-Schauder's nonlinear alternative and Leray-Schauder's degree theory.

2 Preliminaries

In this section,we present notation and some preliminary lemmas that will be used in the proofs of the main results.

Definition 2.1(see[20,21]).The Riemann-Liouville fractional integral of order ϑ≥0,of a function h:(0,∞)→R is defined as

Definition 2.2(see[20,21]).The Riemann-Liouville fractional derivative of order ϑ＞0,of a continuous function h:(0,∞)→R is defined as

where n=[ϑ]+1.

For ϑ＜0,we use the convention that Dϑh=J-ϑh.Also for 0≤ρ＜ϑ,it is valid that DρJϑh=hϑ-ρ.

We note that for ε＞-1 and ε≠ϑ-1,ϑ-2,···,ϑ-n,we have

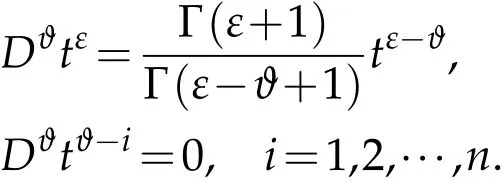
Lemma 2.1(see[16]).Let ϑ＞0 and x∈C(0,T)∩L1(0,T).Then the fractional differential equation Dϑx(t)=0 has a unique solution

where ci∈R,i=1,2,···,n,n=[ϑ]+1.

Lemma 2.2(see[16]).Let ϑ＞0.Then for x∈C(0,T)∩L1(0,T)and Dϑx∈C(0,T)∩L1(0,T),we have

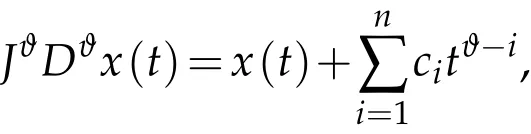
where ci∈R,i=1,2,···,n and n=[ϑ]+1.

Lemma 2.3.For a given h∈C([0,T],R),the linear fractional multi-point boundary value problem

has a unique solution

where

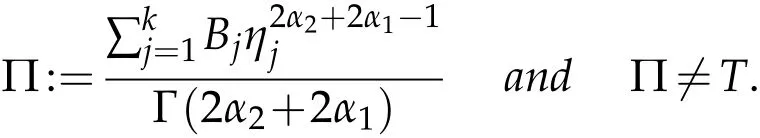
Proof.By Lemma 2.1 and Lemma 2.2,the solution of(2.1)can be written as

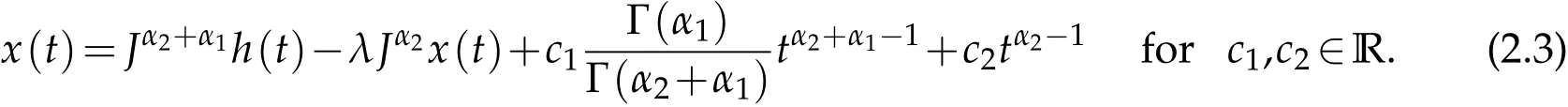
The boundary condition J1-α2x(0)=0 implies that c2=0.Using the relation Dϑtε=,the Eq.(2.3)reduces to

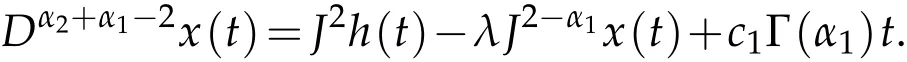
By taking the Riemann-Liouville fractional integral of order α2+α1-1 for(2.3),we get

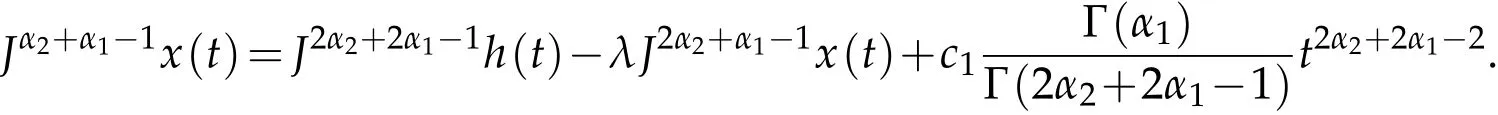
Using the boundary condition

we obtain that

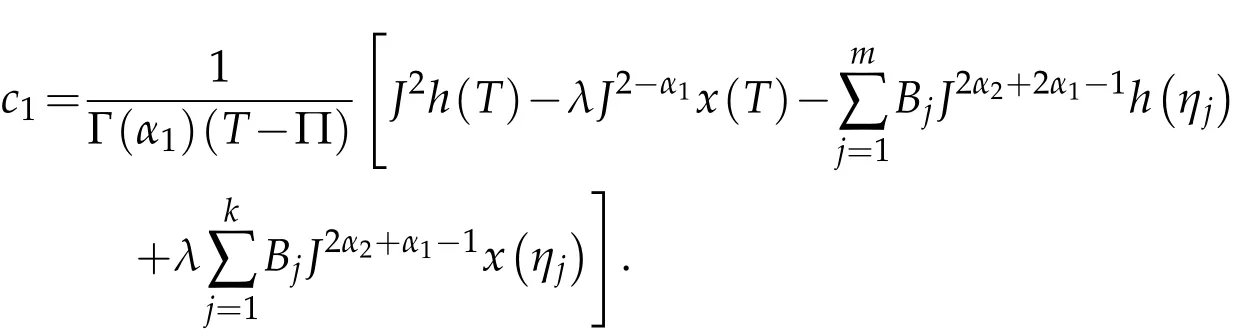
Substituting the value of c0and c1in(2.3),we obtain the solution(2.2).

3 Existence results for multi-point boundary value problem

We denote by X=C([0,T],R)the Banach space of all continuous functions from[0,T]to R endowed with a topology of uniform convergence with the norm defined bykxk=supt∈[0,T]|x(t)|.

In view of Lemma 2.3,we define an operator φ:X→X by:

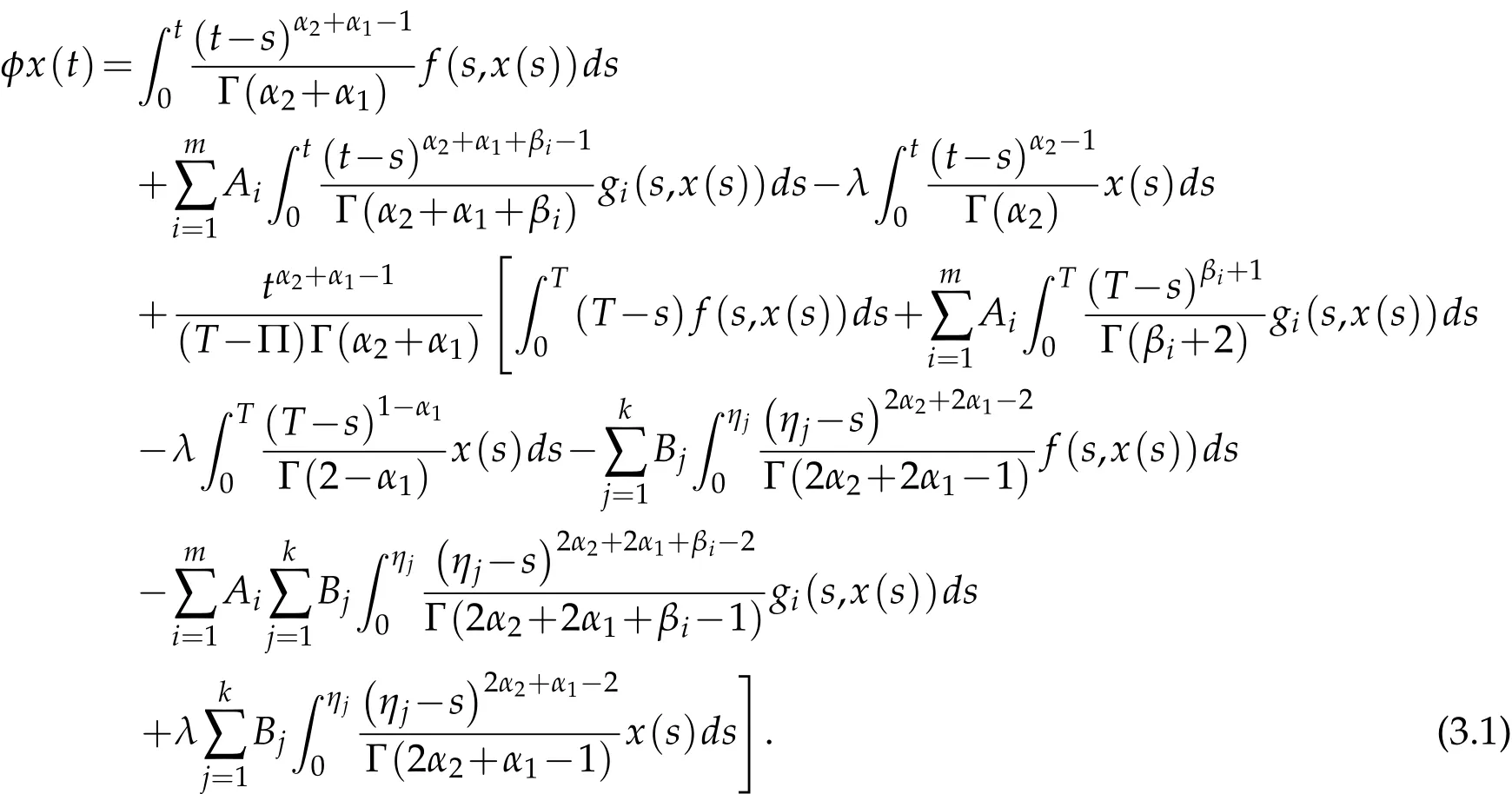
Observe that the existence of a fixed point for the operator φ implies the existence of a solution for the multi-point boundary value problem(1.1).

For convenience we introduce the notations:

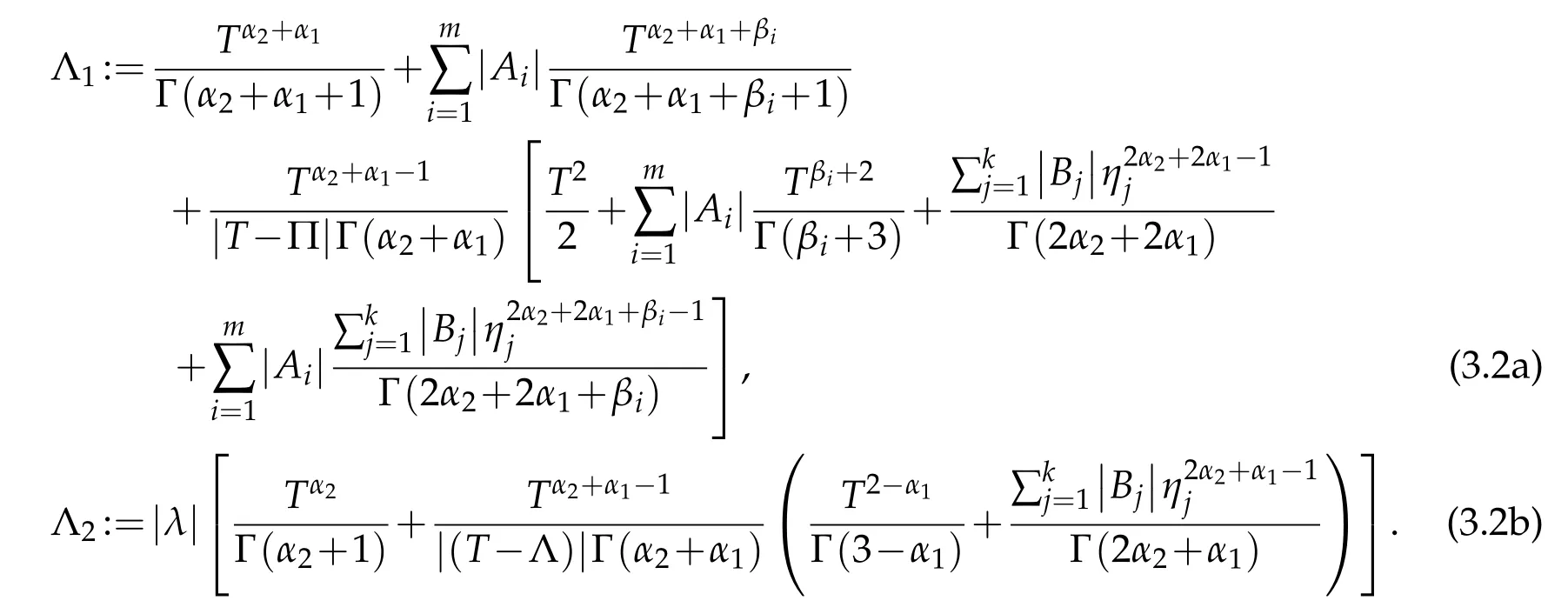
In the following,we prove existence as well as existence and uniqueness results for multipoint boundary value problem(1.1)by applying a variety of fixed point theorems.Now,we present the existence and uniqueness of solutions of multi-point boundary value problem(1.1)by using Banach's fixed point theorem.

Theorem 3.1.Let f,gi:[0,T]×R → R,i=1,···,m be continuous functions satisfying the hypothesis

(H1)there exist nonnegative constants ωi,i=1,···,m+1,such that for all t∈ [0,T]and all x,y∈R,we have

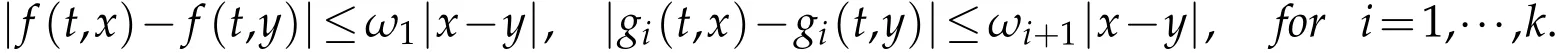
Then the multi-point boundary value problem(1.1)has a unique solution provided by ωΛ1＜1-Λ2,where ω=max{ωi:i=1,···,m+1},Λ1and Λ2are given by(3.2a)and(3.2b),respectively.

Proof.Let us define L=max{Li:i=1,···,m+1},where Liare finite numbers given by L1=supt∈[0,T]|f(t,0)|,Li+1=supt∈[0,T]|hi(t,0)|.Setting

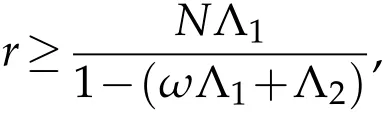
we show that φBr⊂Br,where Br={x∈X:kxk≤r}.

For x∈ Brand for each t∈[0,T],from the definition of φ and hypothesis(H1),we obtain

which implies that φBr⊂Br.Now for x,y∈Brand for any t∈[0,T],we get

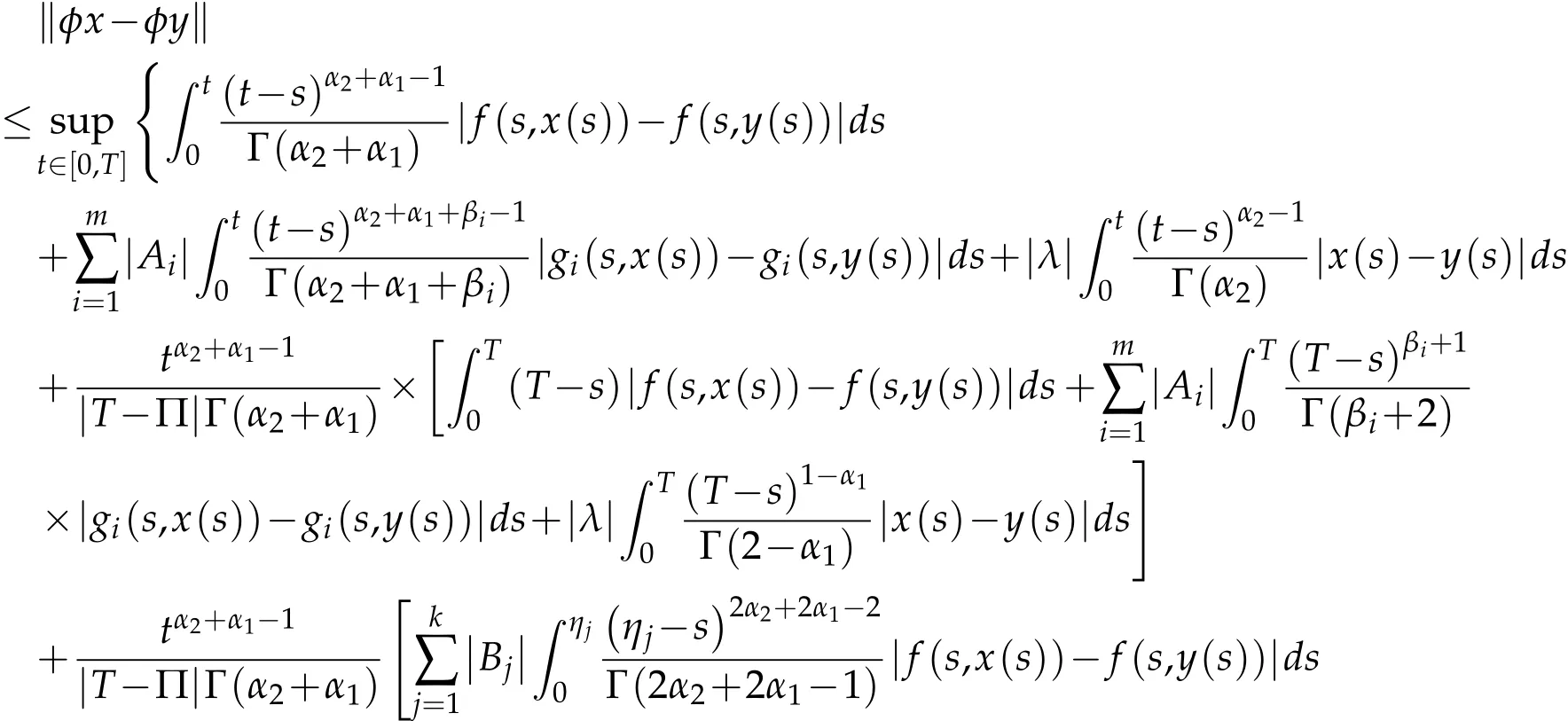
which leads tokφx-φyk≤(ωΛ1+Λ2)kx-yk.Since ωΛ1＜1-Λ2,φ is a contraction mapping.

Also,we give another variant of existence and uniqueness result based on the Hölder inequality.

Theorem 3.2.Let f,gi:[0,T]×R → R,i=1,···,m be continuous functions.In addition we assume that:

(H2)|f(t,x)-f(t,y)|≤u(t)|x-y|,|gi(t,x)-gi(t,y)|≤vi(t)|x-y|,for each t∈[0,T],x,y∈R,where u,vi∈L1δ([0,T],R+),i=1,···,k,and δ∈(0,1).Denote

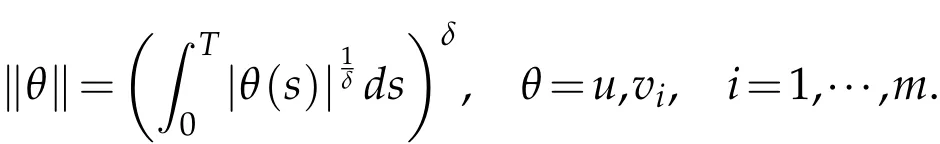
If

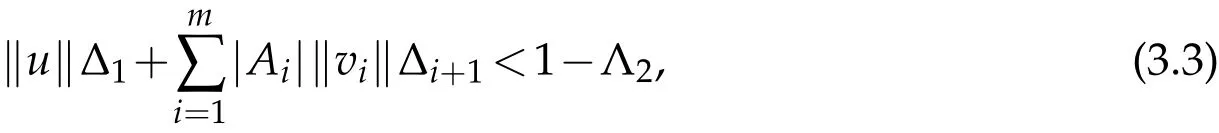
where

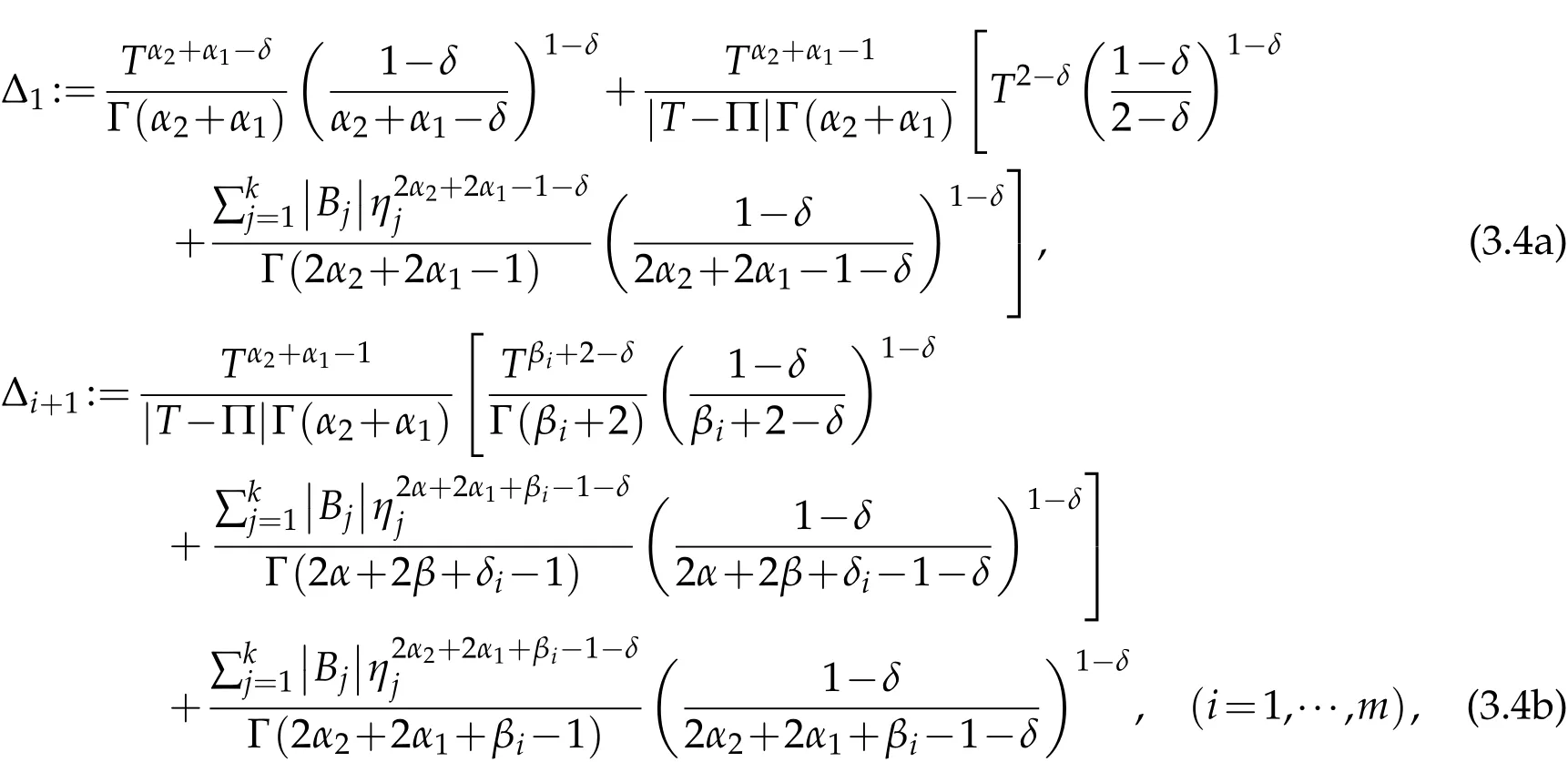
and Λ2is given by(3.2b).Then the multi-point boundary value problem(1.1)has a unique solution.

Proof.For x,y∈X and t∈[0,T],by Hölder inequality and using(H2),we have:

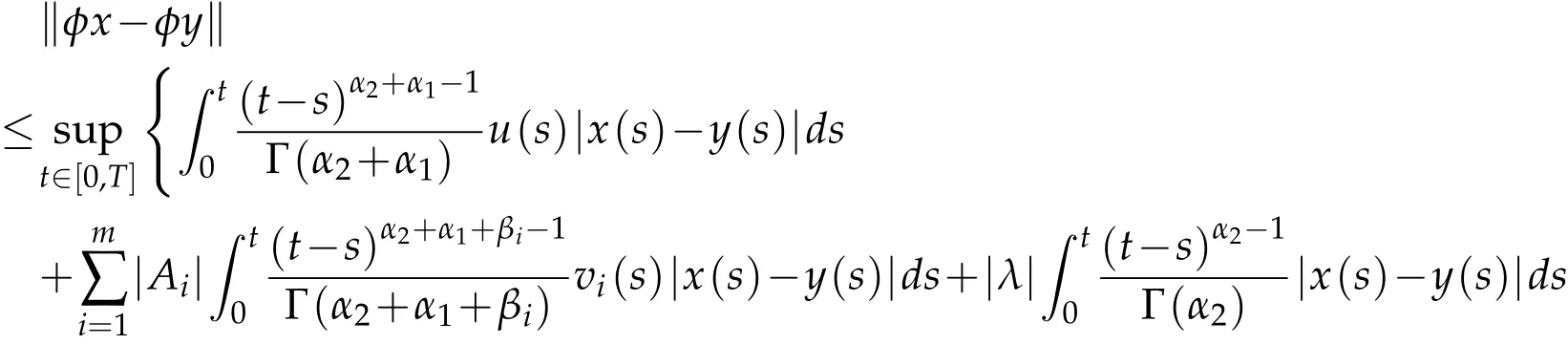
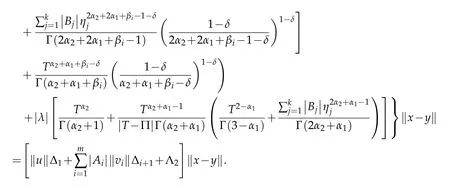
Therefore,

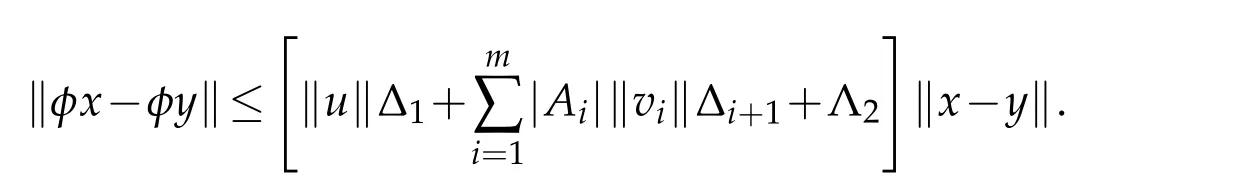
By the condition(3.3),it follows that φ is a contraction mapping.Hence,by the Banach's fixed point theorem φ has a unique fixed point which is the unique solution of the multipoint boundary value problem(1.1).Then,the proof is completed.

Now,we prove the existence of solutions of multi-point boundary value problem(1.1)by applying Leray-Schauder nonlinear alternative[25].

Theorem 3.3(Nonlinear alternative for single valued maps).Let E be a Banach space,C a closed,convex subset of E,Θ an open subset of C and 0∈Θ.Suppose that φ:→C is a continuous,compact(that is,is a relatively compact subset of C)map.Then,either

(ii)there is a x∈∂Θ (the boundary of Θ in C)and σ∈(0,1)with x=σφx.

Theorem 3.4.Assume that f,gi:[0,T]×R→R,i=1,···,m are continuous functions.Suppose that:

(H3)there exist nondecreasing functions ψ,ψi:[0,∞)→ [0,∞),i=1,···,k and functions b,bi∈L1([0,T],R+),i=1,···,m such that

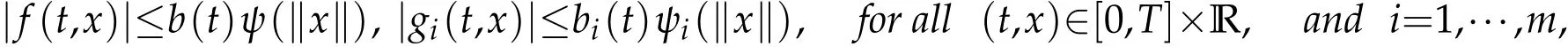
(H4)there exists a constant N＞0 such that

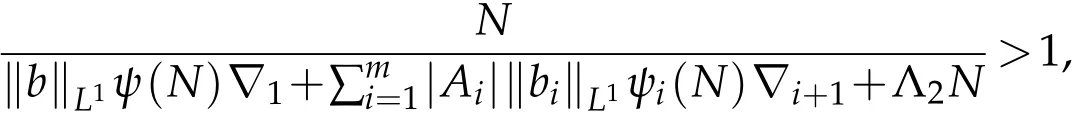
where

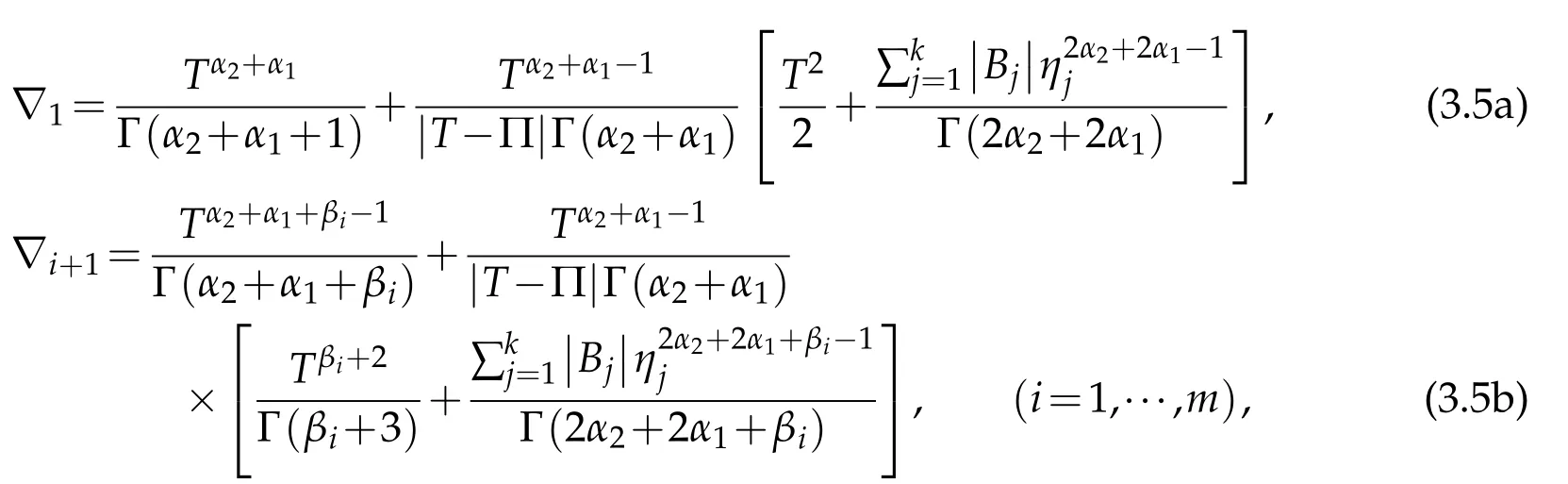
and Λ2is given by(3.2b).Then the multi-point boundary value problem(1.1)has at least one solution on[0,T].

Proof.Let the operator φ:X → X be defined by(3.1).Firstly,we will show that φ maps bounded sets into bounded sets in X.For a number r＞0,let Br={x∈X:kxk≤r}be a bounded set in X.Then,for t∈[0,T]and(H3),we have

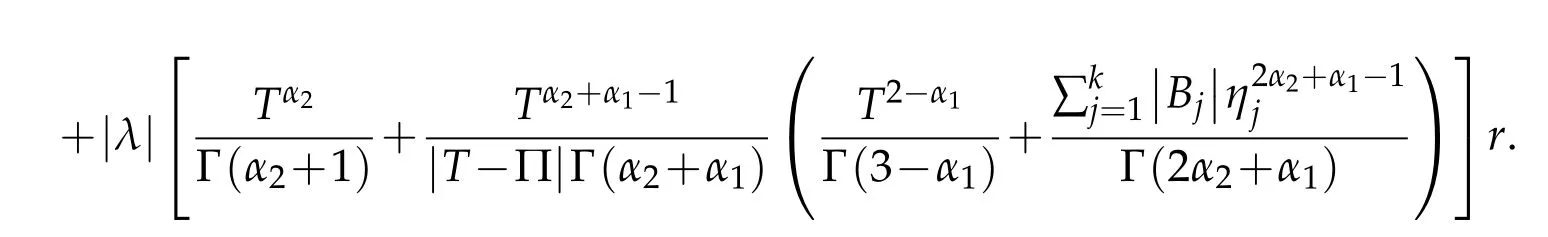
Consequently,

Therefore

Thus,φ maps bounded sets into bounded sets in X.

Next,we show that φ maps bounded sets into equicontinuous sets of X.Let t1,t2∈[0,T]with t1＜t2and x∈Br.Then,we have

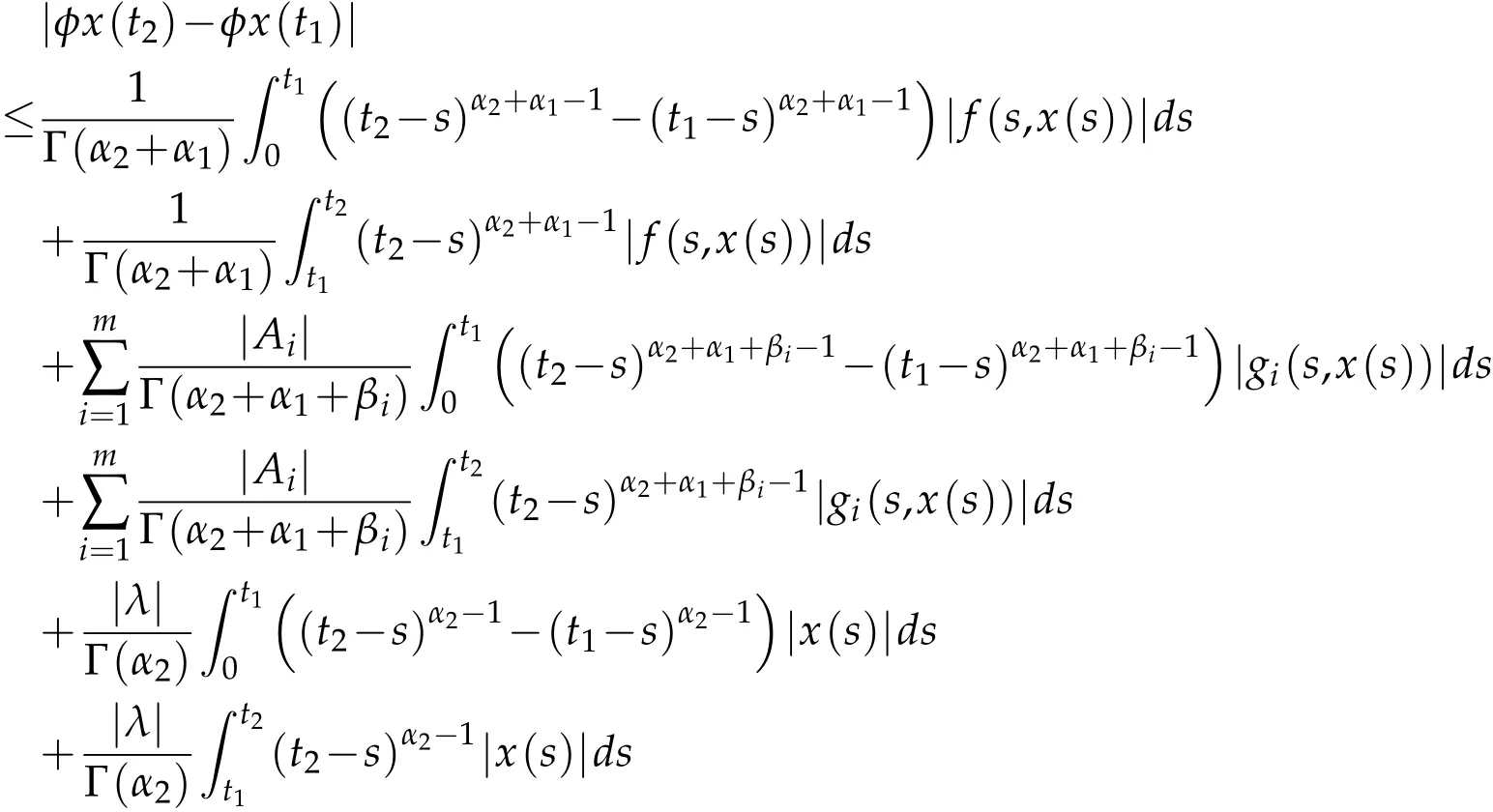
Obviously,the right-hand side of the above inequality tends to zero independently of x∈Bras t2-t1→0.Therefore,φ:X→X is completely continuous by application of the Arzela-Ascoli theorem.

Now,we can conclude the result by using the Leray-Schauder's nonlinear alternative theorem.Consider the equation x=σφx for 0＜σ＜1 and assume that x be a solution.Then,using the computations in proving that φ is bounded,we have

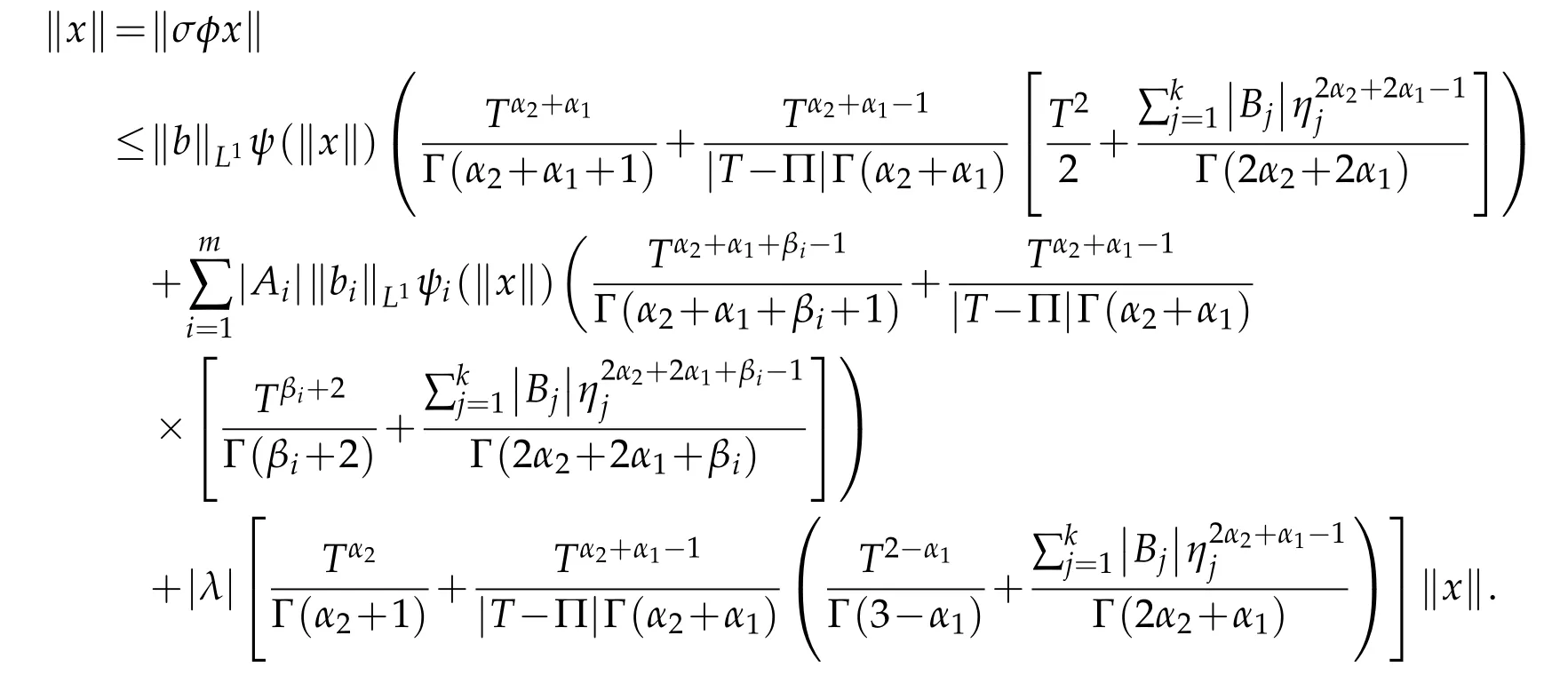
Therefore,

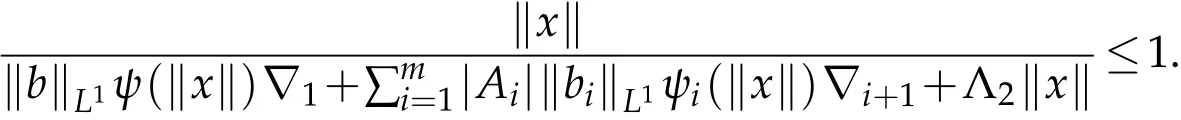
By(H4),there exists N such that N≠kxk.Let us set

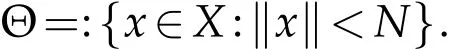
We also prove the existence of solutions of multi-point boundary value problem(1.1)by using Leray-Schauder degree.

Theorem 3.5.Let f,gi:[0,T]×R→R,i=1,···,m,be continuous functions.Suppose that(H5)there exist constantsand Mi＞0,i=1,···,m+1 such that

where a=max{ai:i=1,···,+1},M=max{Mi:i=1,···,m+1}.Then the multi-point bound

ary value problem(1.1)has at least one solution on[0,T].

Proof.We define an operator φ:X→X as in(3.1)and consider the fixed point equation

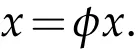
We shall prove that there exists a fixed point x∈X satisfying(1.1).It is sufficient to show that φ:→X satisfies

where

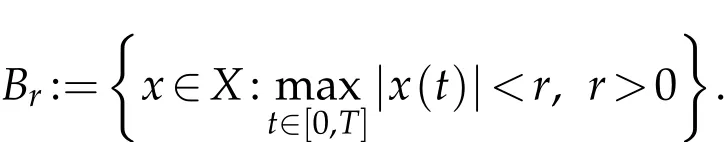
We define

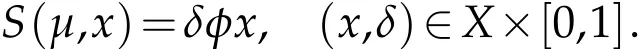
As shown in Theorem 3.4, the operator f is continuous, uniformly bounded, and equicontinuous.Then,by the Arzela-Ascoli theorem,a continuous map sδdefined by sδ=x-S(µ,x)=x-δφx is completely continuous.If(3.6)holds,then the following Leray-Schauder degrees are well defined and by the homotopy invariance of topological degree,it follows that

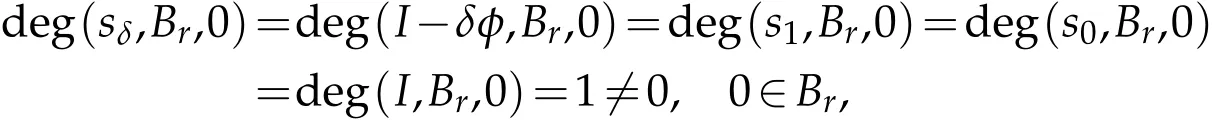
where I denotes the identity operator.By the nonzero property of Leray-Schauder's degree,s1(x)=x-φx=0 for at least one x∈Br.In order to prove(3.6),we assume that x=δφx for some δ∈[0,1]and for all t∈[0,T].Then

Taking norm supt∈[0,T]|x(t)|=kxk,we get

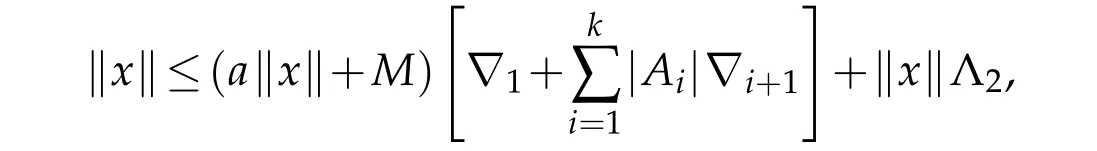
which implies that

4 Application

To illustrate our main results,we treat the following examples.

Example 4.1.Let us consider the following multi-point boundary value problem

Hence,

and

Therefore,we have

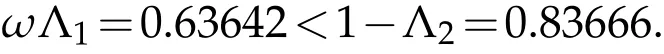
Hence,all the hypotheses of Theorem 3.1 are satisfied.Thus,by the conclusion of Theorem 3.1,multi-point boundary value problem(4.1)has a unique solution.

Example 4.2.As a second illustrative example,let us take

Cleary,

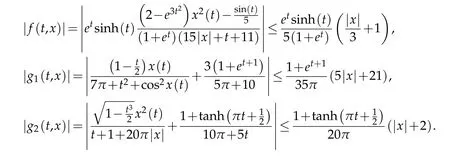
which implies N＞0.27128.Hence,by Theorem 3.4,the multi-point boundary value problem(4.2)has at least one solution on[0,1].

Example 4.3.Our third example is the following

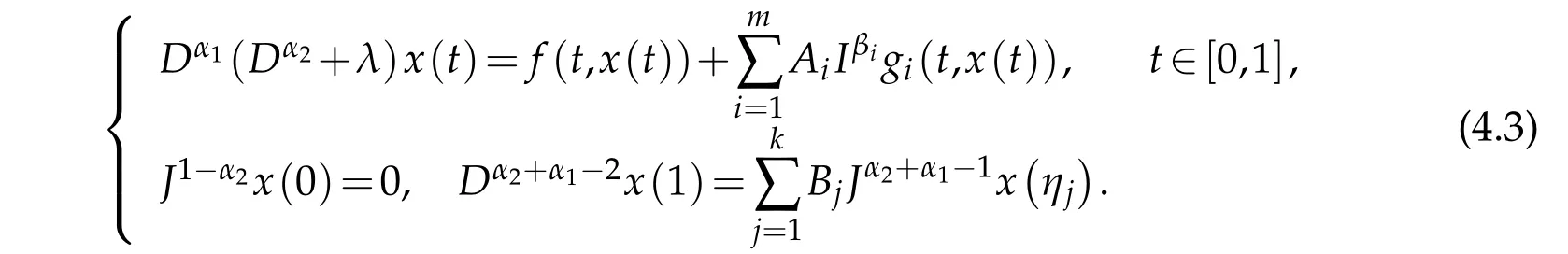
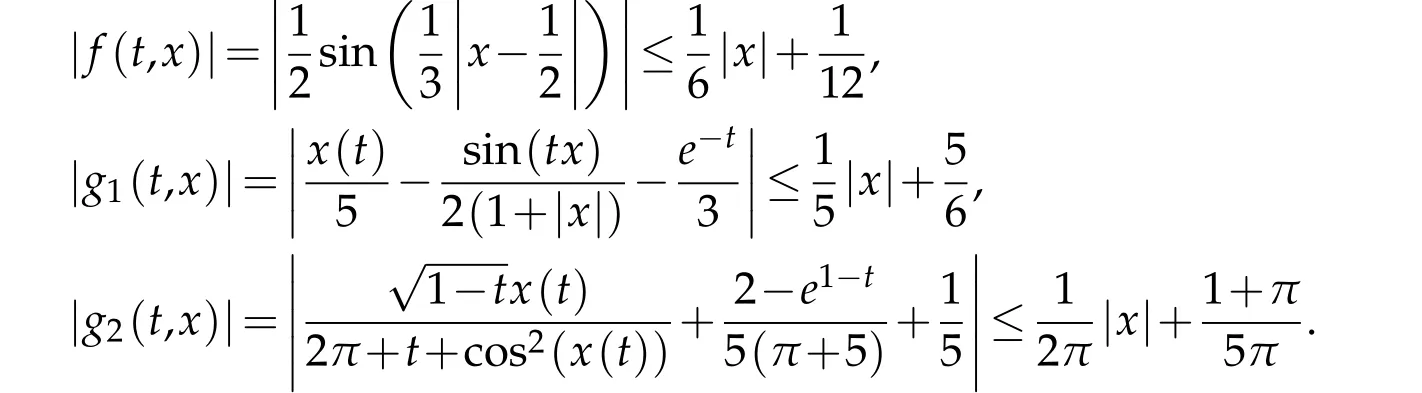
Cleary,

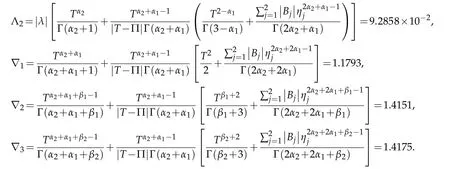
Thus,all the conditions of Theorem 3.5 are satisfied and consequently the multi-point boundary value problem(4.3)has at least one solution.