Weighted Boundedness of Commutators of Generalized Calderón-Zygmund Operators

Cuilan Wu,Yunjie Wangand Lisheng Shu

1School of Mathematics and Statistics,Jiangsu Normal University,Xuzhou 221116,Jiangsu,China

2Kewen Institute,Jiangsu Normal University,Xuzhou 221116,Jiangsu,China

3College of Mathematics and Computer Science,Anhui Normal University,Wuhu 241003,Anhui,China

Abstract.[b,T]denotes the commutator of generalized Calderón-Zygmund operators T with Lipschitz function b,where b∈ Lipβ(Rn),(0＜ β ≤ 1)and T is a θ(t)-type Calderón-Zygmund operator.The commutator[b,T]generated by b and T is defined by

In this paper, the authors discuss the boundedness of the commutator [b,T] on weighted Hardy spaces and weighted Herz type Hardy spaces and prove that[b,T]is bounded from Hp(ωp)to Lq(ωq),and fromThe results extend and generalize the well-known ones in[7].

Key Words:Commutator,Lipschitz function,weighted hardy space,Herz space.

1 Introduction

The singular integral operators and their commutators have been extensively studied in recent years,and the results are plentiful and substantial.But the commutators of θ(t)-type Calderón-Zygmund operators which were introduced in[1]by Yabuta and in[2]by Lizhong Peng,have not been discussed extensively.However,the introduction of this kind of operators has profound background of partial differential equation.Lin Haibo[3]obtained weighted estimates for commutators generated by the multilinear Calderón-Zygmund operators and RMO(µ)functions.In 2014,Hu Guoen[4]gave the weighted norm inequalities for multilinear Calderón-Zygmund operators on nonhomogeneous metric measure spaces.The studies of Calderón-Zygmund operators and commutators see[5,6].In[7],Zhao Kai etc.studied the boundedness of commutators of generalized Calderón-Zygmund operators on classical Hardy spaces and Herz type Hardy spaces.

Inspired by the results in[7]and other papers,we study the commutators generated by generalized Calderón-Zygmund operators and Lipschitz functions. By the Minkowski integral inequality,Holder inequality and Jensen inequality to control some inequalities,we obatin the boundedness of the commutator[b,T]generated by θ(t)-type Calderón-Zygmund operators T and Lipschitz function b on weighted Hardy spaces and weighted Herz type Hardy spaces.

First of all,let us introduce the definitions of θ(t)-type Calderón-Zygmund operators.

Definition 1.1.Suppose that T is a bounded operator from Schwartz class S(Rn)to its dual S′(Rn),satisfying the following conditions:

(i)There exists C＞0,such that for any

(ii)There exists a continuous function k(x,y)defined on Ω ={(x,y)∈ Rn×Rn:x≠y}

and C＞0 such that

a)k(x,y)≤C|x-y|-nfor all(x,y)∈Ω.

b)for all x,x0,y∈Rnwith 2|x-x0|＜|y-x0|,

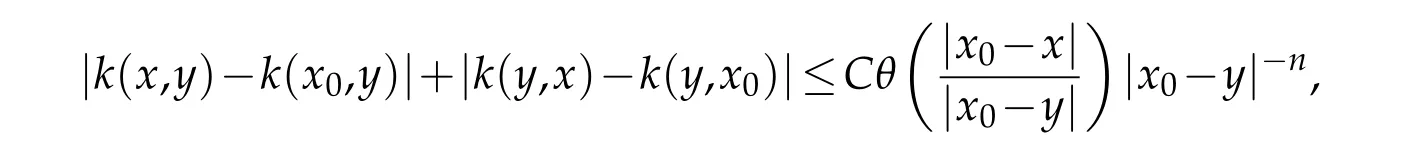
where θ(t)is a nonnegative nondecreasing function on[0,∞)withand θ(0)=0,θ(2t)≤Cθ(t).

Then T is said to be a θ(t)-type Calderón-Zygmund operator.

For some properties of θ(t)-type Calderón-Zygmund operator defined above,especially the boundedness on some spaces,see[1]and[2]etc for details.

Similar to the definitions of other commutators,we introduce the definition of commutator generated by θ(t)-type Calderón-Zygmund operator and Lipschitz function as follows.

Definition 1.2.Let b∈Lipβ(Rn),and T be a θ(t)-type Calderón-Zygmund operator.The commutator[b,T]generated by b and T is defined by

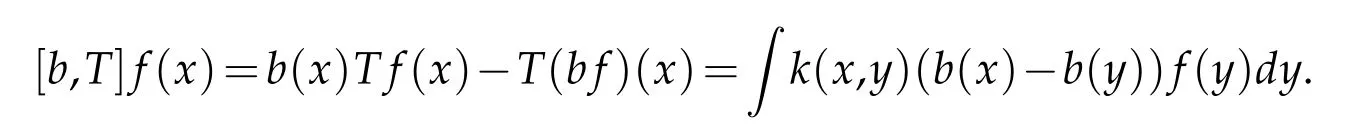
For β＞0,the Lipschitz space Lipβ(Rn)is defined by

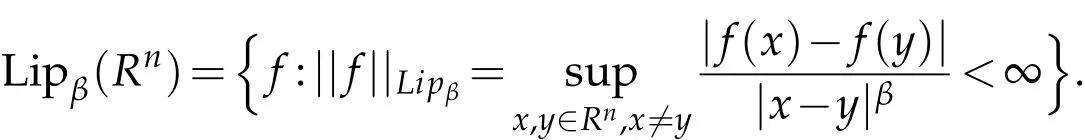
Obviously,if β＞1,then Lipβ(Rn)only includes constant,and[b,T]≡0 is trivial.So we restrict 0＜β≤1.

Secondly,let us introduce Riesz integral Iαand its boundedness on Lebesgue spaces which are useful to the proofs of theorems in the following.

Definition 1.3(see[8]).For 0＜α＜n,Riesz integral Iαis defined by

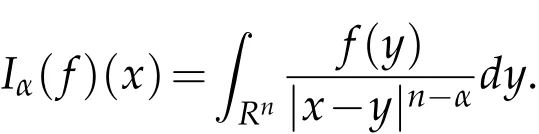
In the paper,we will study the boundedness of the commutator[b,T]on weighted Hardy spaces and Herz type Hardy spaces in Sections 2 and 3,respectively.

2 Boundedness on weighted Hardy spaces

To state our results,let us recall some definitions.In the following definitions,the function ω is locally integrable nonnegative function on Rn.Moreover,C＞0 and B denotes a ball in Rn,|B|denotes the Lebesgue measure of B.

The definition of Ap(1≤p≤∞).Let ω be nonnegative,locally integrable.ω is said to belong to Ap(1＜p＜∞)if

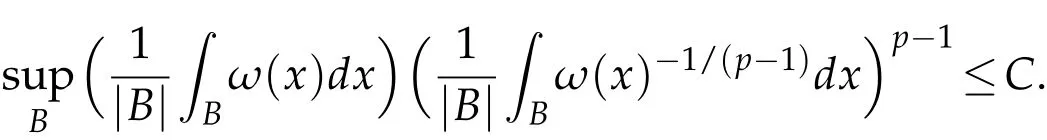
For the case p=1,ω∈A1if

For the case p=∞,ω∈A∞if ω∈Apfor some p＞1.We denote qω=inf{q＞1:ω∈Aq}the critical index of ω and set the weighted measure ω(E)=REω(x)dx.

The definition of A(p,q)(1＜p,q＜∞).Let ω be nonnegative,locally integrable.ω is said to belong to A(p,q)if

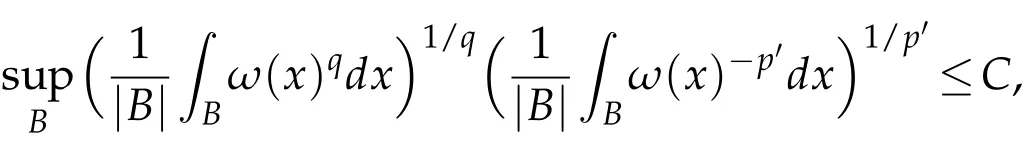
where p′=p/(p-1).

The definition of reverse Hölder condition.If there exists r＞1 such that

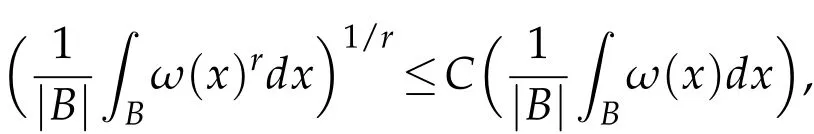
then ω is said to satisfy the reverse Hölder condition of order r and is written by ω∈RHr.It follows from Hölder inequality that ω∈RHrimplies ω∈RHsfor s＜r.It is known that if ω ∈RHr(r＞1)then ω ∈RHr+εfor some ε＞0.

The elementary properties of Ap(see[10]).

(a)A1⊂Ap⊂Aqif 1＜p＜q＜∞.

(b) ω(x)∈ Apif and only if ω(x)1-p′∈ Ap′.

(c)If ω(x)∈ Ap,then there exists an ε＞0 such that p-ε＞1 and ω(x)∈ Ap-ε.

(d)If ω(x)∈ Ap,then there exists an ε＞0 such that ω(x)1+ε∈ Ap.

(e)If ω(x)∈ Ap,then for any 0＜ε＜1,ω(x)ε∈ Ap.

(f)If ω(x)∈Ap,then there are C＞0 and ε＞0,such that,for any B⊂Rn,

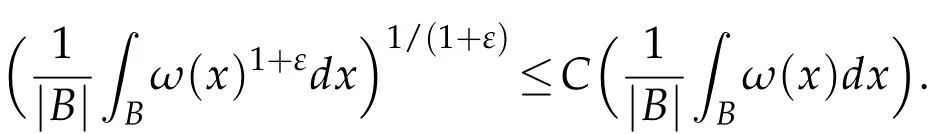
The relations between Apand A(p,q)(see[10]).Suppose that 0＜α＜n,1＜p＜n/α and 1/q=1/p-α/n.Then we have the following conclusions:

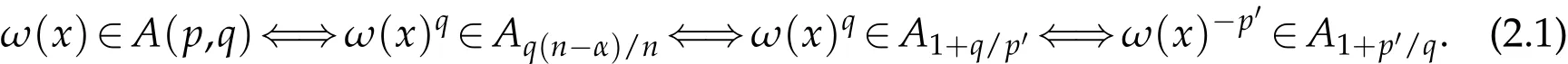
To prove our results,we need the following lemmas.

Lemma 2.1(see[9]).If 0＜α＜n,1＜p＜n/α,1/p-1/q=α/n and ω(x)∈A(p,q),then there is a constant C＞0,independent of f,such that

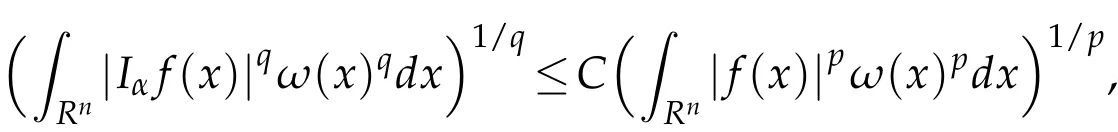
The boundedness of commutator[b,T]on the weighted Lebesgue spaces is as follows.

Lemma 2.2.Let b∈ Lipβ(Rn)(0＜β≤1),1＜p＜n/β,1/q=1/p-β/n,1＜p＜q＜∞,and ω(x)∈A(p,q).Then the commutator[b,T]is bounded from Lp(ωp)to Lq(ωq).

Proof.Let f∈Lp(ωp),then

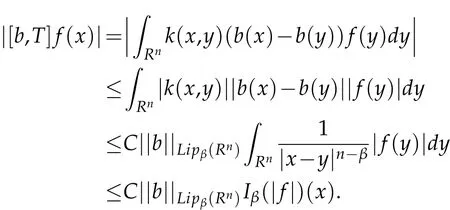
Applying Lemma 2.1 for Iβ,we have

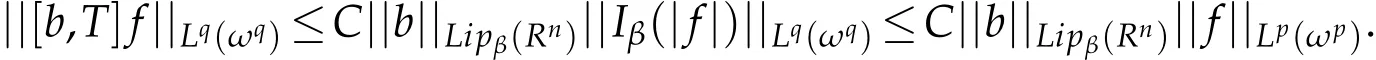
This completes the proof of Lemma 2.2.

Lemma 2.3(see[11]).Let r＞1,then ωr∈ A∞if and only if ω∈RHr.

16周后将30只大鼠随机分为模型对照组与DC疫苗组，DC疫苗组分别于造模后第2、5、8周的周一、三、五、七皮下多点注射DC疫苗，模型组皮下注射等量生理盐水。

For any ball B and any λ＞0,we denote by λB the ball with the same center as B but with λ times the radius.We have the estimate for ω(λB)as follows:

Lemma 2.4(see[12]).Let ω∈Ap,p≥1,then for any ball B and λ＞1,

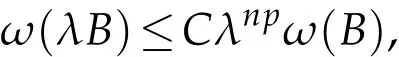
i.e.,

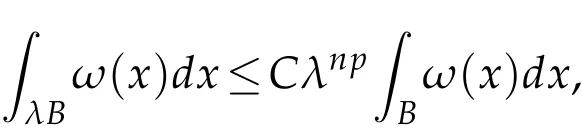
where C does not depend on B nor on λ.

In order to study the boundedness of[b,T]generated by θ(t)-type Calderón-Zygmund operator T and Lipschitz function b on weighted Hardy spaces,let us first introduce the atomic decomposition theory and molecular characterization(see[13,14])for weighted Hardy space.

Definition 2.1.Let 0＜p≤1≤q≤∞ and p≠q such that ω∈Aqwith critical index qω.Set[·]the integer function.For s∈Z satisfying s≥[n(qω/p-1)],a real-valued function a(x)is called(p,q,s)-atom centered at x0with respect to ω (or ω -(p,q,s)-atom centered at x0)if

(i)a∈Lq(ω)and is supported in a ball B with center x0;

(ii)||a||Lq(ω)≤ω(B)1/q-1/p,where ω(B)=RBω(x)dx;

Lemma 2.5(see[13,14]).Let ω∈Aq,0＜p≤1≤q≤∞ and p≠q.For each f∈Hp(ω),there exists a sequence{ai}of ω-(p,q,s)-atoms,s≥[n(qω/p-1)]and a sequence{λi}of real numbers withsuch that f=∑λiaiboth in the sense of distributions and in the Hp(ω)norm.

Remark 2.1.For q=∞,from||f||L∞(ω)=||f||L∞ and(ii)in Definition 2.1,it follows that

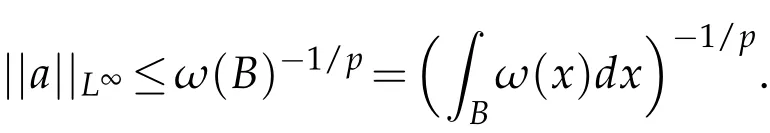
Our result can be stated as follows.

Theorem 2.1.Let b∈ Lipβ(Rn)(0＜β≤1),n/(n+β)＜p≤1,1/q=1/p-β/n.If

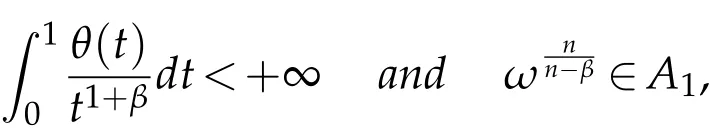
then the commutator[b,T]is bounded from Hp(ωp)to Lq(ωq).

Proof.By Lemma 2.5,it suffices to show that there is a constant C＞0 such that

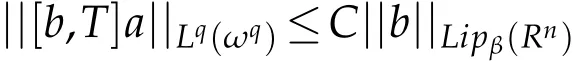
for any ωp-(p,∞,s)-atom a(s≥[n(1/p-1)]).

Given a ωp-(p,∞,s)-atom a with suppa⊂ B=B(x0,r),it is easy to see that

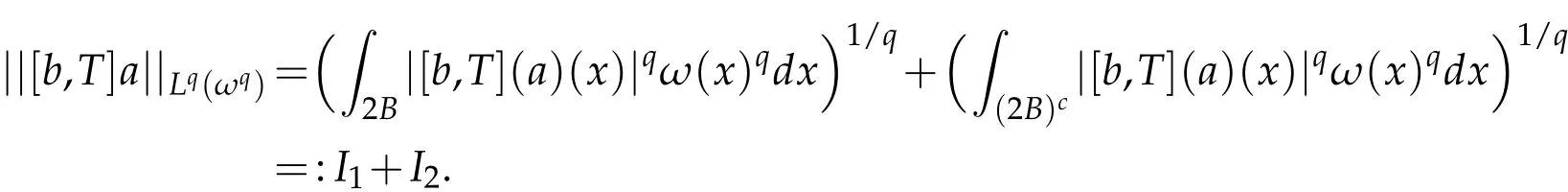
For I1,it is known that ωn/(n-β)∈ A1implies ωn(1+δ)/(n-β)∈ A1for some δ＞0.Choose p1and q1such that q1=n(1+δ)/(n-β)and 1/q1=1/p1-β/n.Obviously,1＜p1＜n/β and q1＞n/(n-β)≥q.It follows from ωq1∈A1that ω∈A(p1,q1).Applying Hölder's inequality and the(Lp1(ωp1),(Lq1(ωq1))boundedness of[b,T]in Lemma 2.2,we get

Since ωq1∈ A1⊂ A∞,i.e.,(ωp)q1/p∈ A1⊂ A∞,by Lemma 2.3,we have ωp∈RHq1/pand hence ωp∈RHp1/p.The definition of the reverse Hölder condition gives

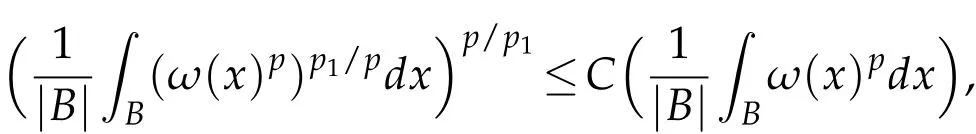
i.e.,

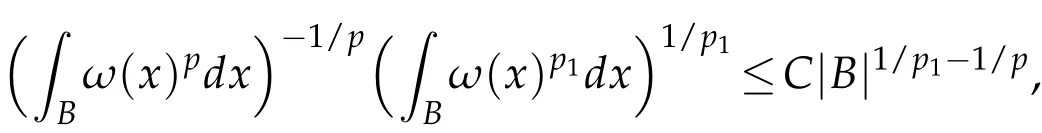
which implies

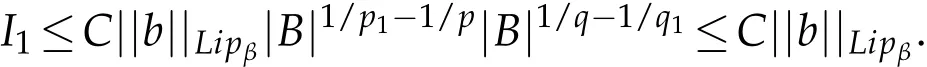
For I2,we have

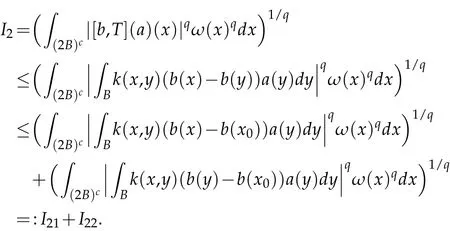
Observe that from x∈(2B)cand y∈B=B(x0,r),it follows that|x-y|～|x-x0|,then

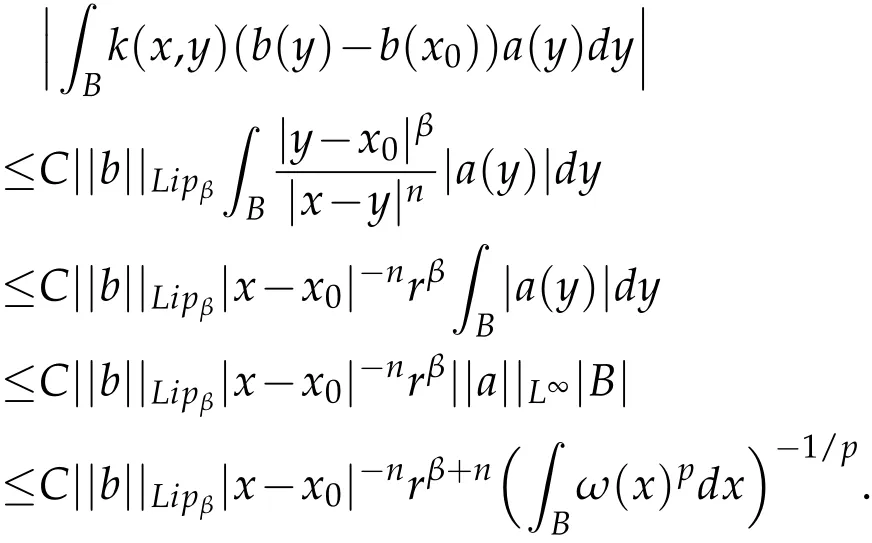
Therefore,

Since 1＜q≤n/(n-β)and ωn/(n-β)∈ A1,we have ωq∈ A1.Thus Lemma 2.4 implies ωq(2k+1B)≤C(2k+1)nωq(B),i.e.,

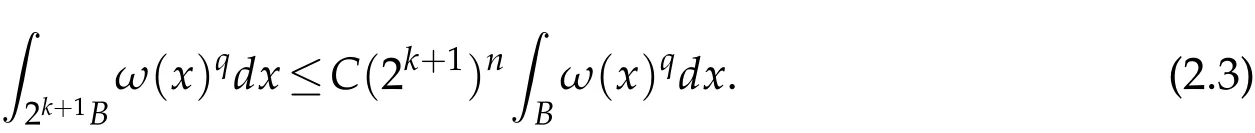
It follows from(2.3)that

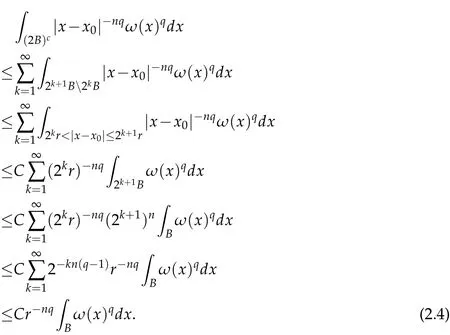
Thus,by(2.2)and(2.4),we get

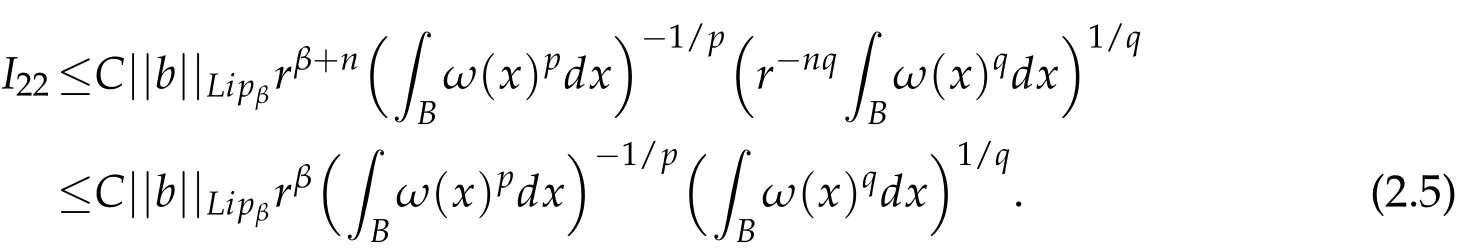
Since q1＞n/(n-β)≥q＞p,ωn/(n-β)∈A1,we have ωq∈A1⊂A∞,i.e.,(ωp)q/p∈A1⊂A∞,by Lemma 2.3,we have ωp∈ RHq/pand hence

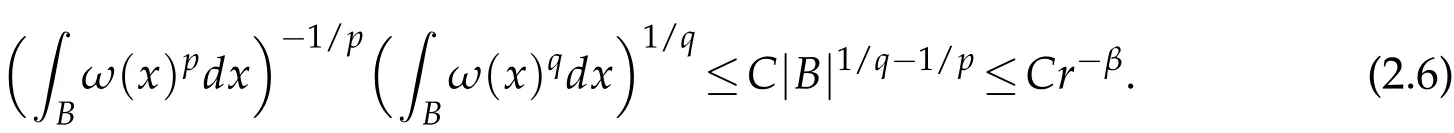
By(2.5)and(2.6),we obtain

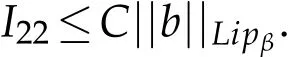
For I21,by the vanishing condition of a,we have

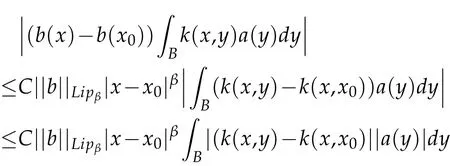
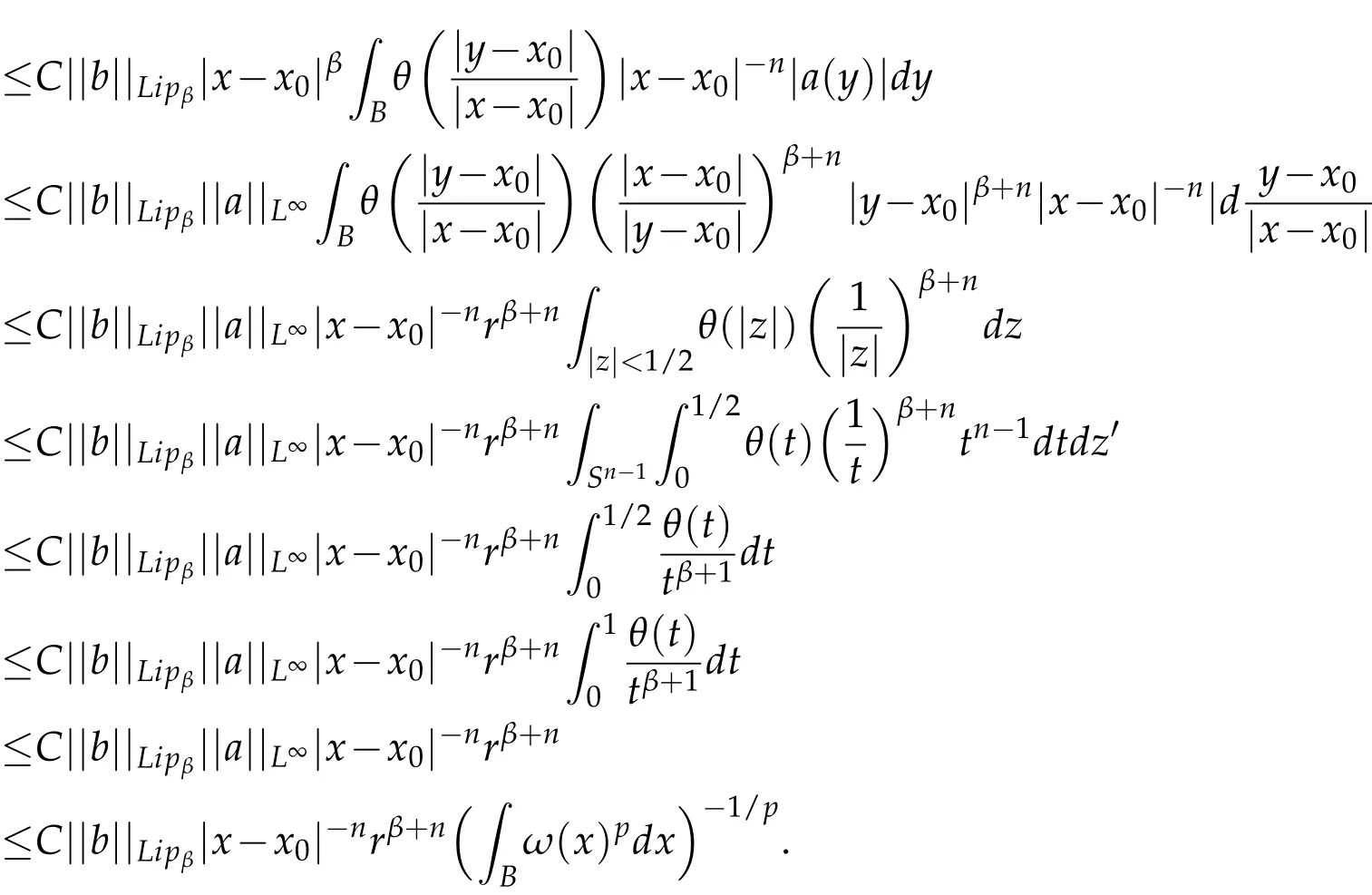
Therefore,

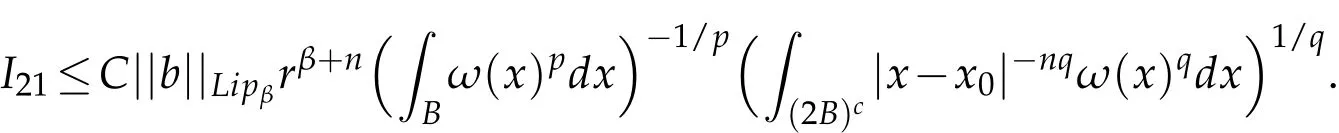
Similar to the estimate for I22,we get

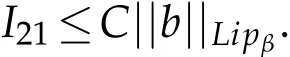
Combing the estimates for I1and I2,we obtain

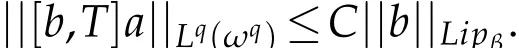
This completes the proof of Theorem 2.1.

3 Boundedness on weighted Herz-type Hardy spaces

In this section,we consider the boundedness of the commutator[b,T]generated by θ(t)-type Calderón-Zygmund operator T and Lipschitz function b on weighted Herztype Hardy spaces.Let us now begin with some notations(see[15]for details).

Definition 3.1.Let Bk={x∈Rn:|x|≤2k},Ck=BkBk-1and χk=χCkbe the characteristic function of the set Ckfor k∈Z.Let 0＜α＜∞,0＜p＜∞,1＜q＜∞,and ω1,ω2be nonnegative weight functions.

1)The homogeneous weighted Herz space(ω1,ω2)is defined by

where

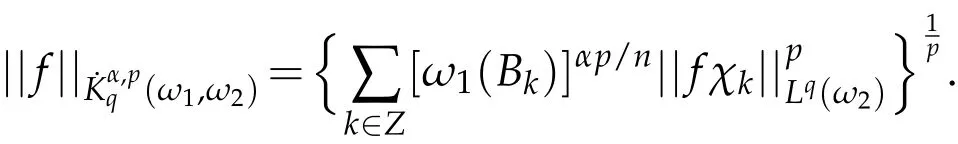
2)The non-homogeneous weighted Herz space(ω1,ω2)is defined by

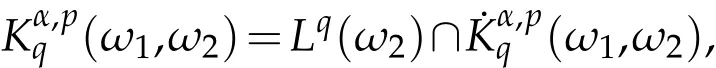
and

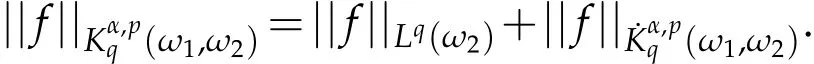
Definition 3.2.Let ω1,ω2∈A1,0＜p＜∞,1＜q＜∞,and 0＜α＜∞.

1)The homogeneous weighted Herz-type Hardy space(ω1,ω2)is defined by

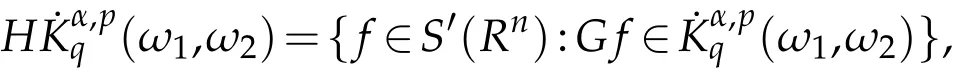
and

2)The non-homogeneous weighted Herz-type Hardy space(ω1,ω2)is defined by

and

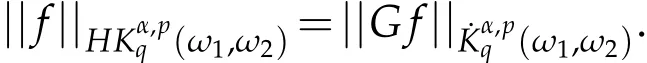
Here,S′(Rn)is the space of the tempered distributions on Rnand G(f)is the Grand maximal function of f,which is defined by

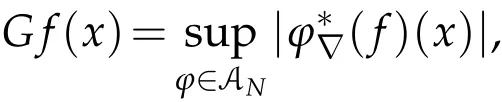
where AN={ϕ∈S(Rn):sup|α|,|β|≤N|xαDβϕ(x)|≤1}and N≥n+1.

The weighted Herz-type Hardy spaces have central atomic decomposition characterizations stated as follows.

Definition 3.3.Let ω1,ω2∈A1,1＜q＜∞,and n(1-1/q)≤α＜∞,s≥[α-n(1-1/q)].A function a(x)on Rnis called a central(α,q;ω1,ω2)atom,if

(i)There exists r＞0,such that suppa⊂B(0,r)={x∈Rn:|x|＜r};

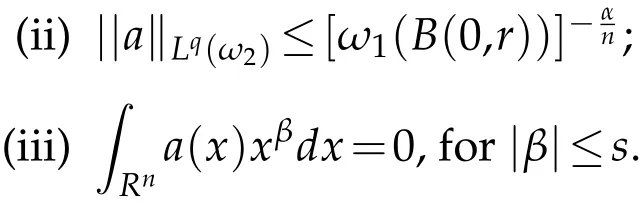
Lemma 3.1.Let ω1,ω2∈A1,0＜p＜∞,1＜q＜∞,n(1-1/q)≤α.A distribution f on Rnbelongs to(ω1,ω2)if and only if f can be written as

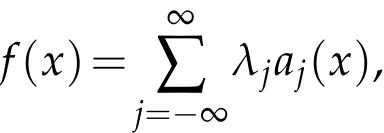
in the sense of distribution,where ajis a central(α,q;ω1,ω2)atom with the support Bj,and∑j∈z|λj|p＜∞.Moreover,

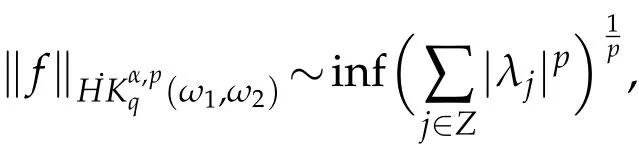
where the in fimum is taken over all tomic decompositions of f.

Lemma 3.2(see[16]).If ω∈Ap,1≤p＜∞,then there are C＞0 and δ(0＜δ＜1)such that

In what follows,we give the boundedness result for[b,T]on Herz-type Hardy spaces.

Theorem 3.1.Let b∈ Lipβ(Rn)(0＜β≤1),0＜p＜∞,1＜q1,q2＜∞,1/q2=1/q1-β/n,and n(1-1/q1)≤α＜n(1-1/q1)+β.Suppose thatthen the commutator[b,T]is bounded fromProof.By Lemma 3.1,we writewhere akis a centralatom with support Bk=B(0,2k)and.Then we have

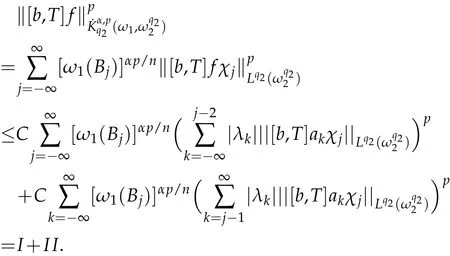
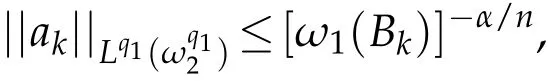
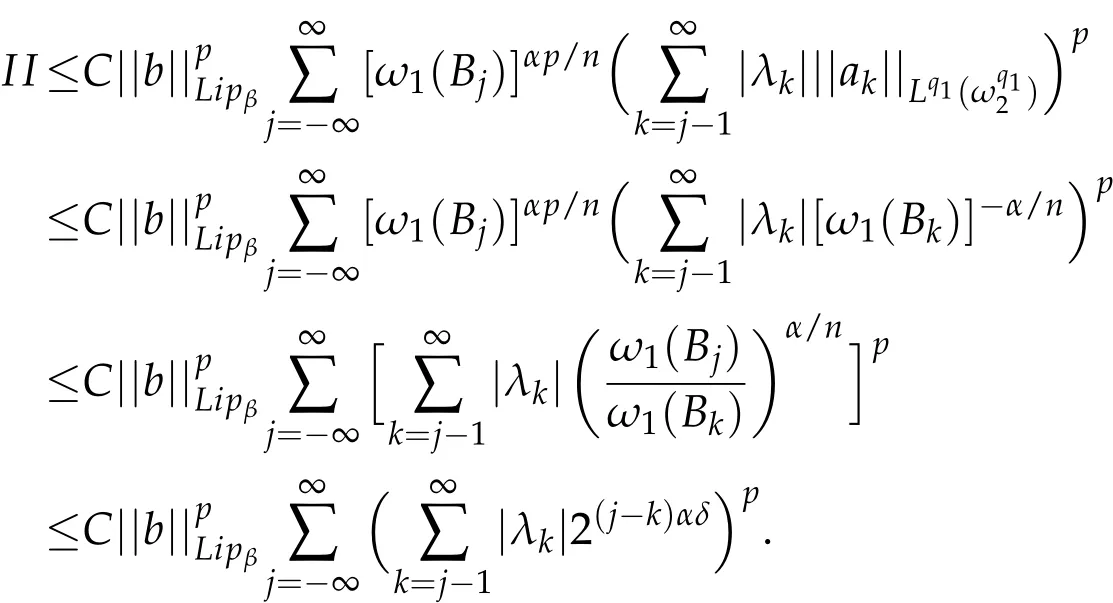
When 0＜p≤1,we get

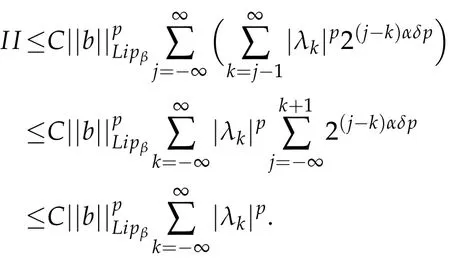
If p＞1,by Hölder's inequality,we get

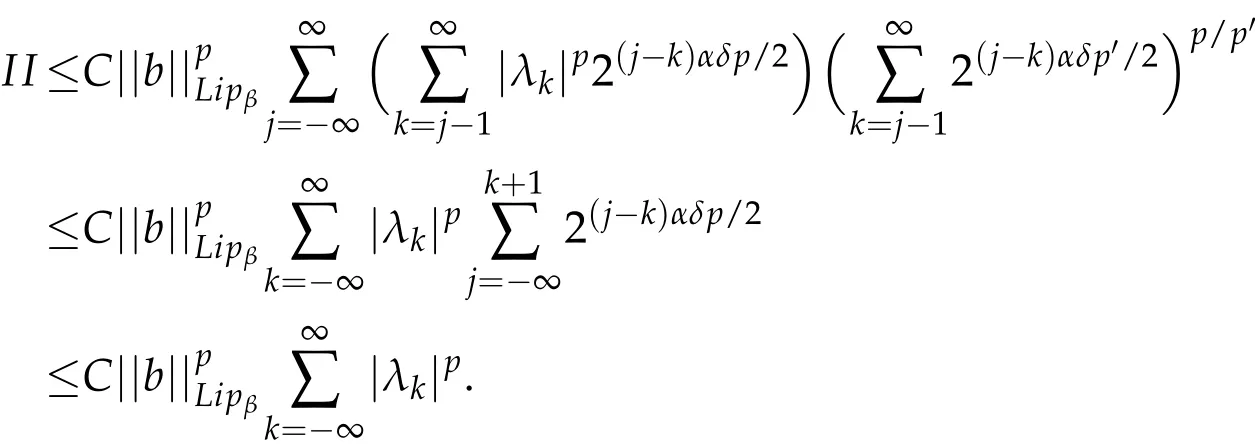
Let us now estimate I.Note that

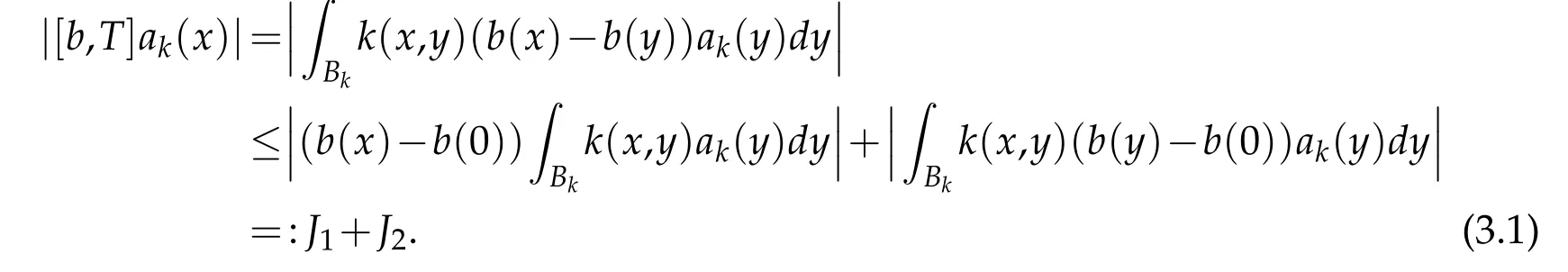
Observe that x∈Cj,y∈Bk,k≤j-2,it follows that|x-y|～|x|.Then by Hölder's inequality,

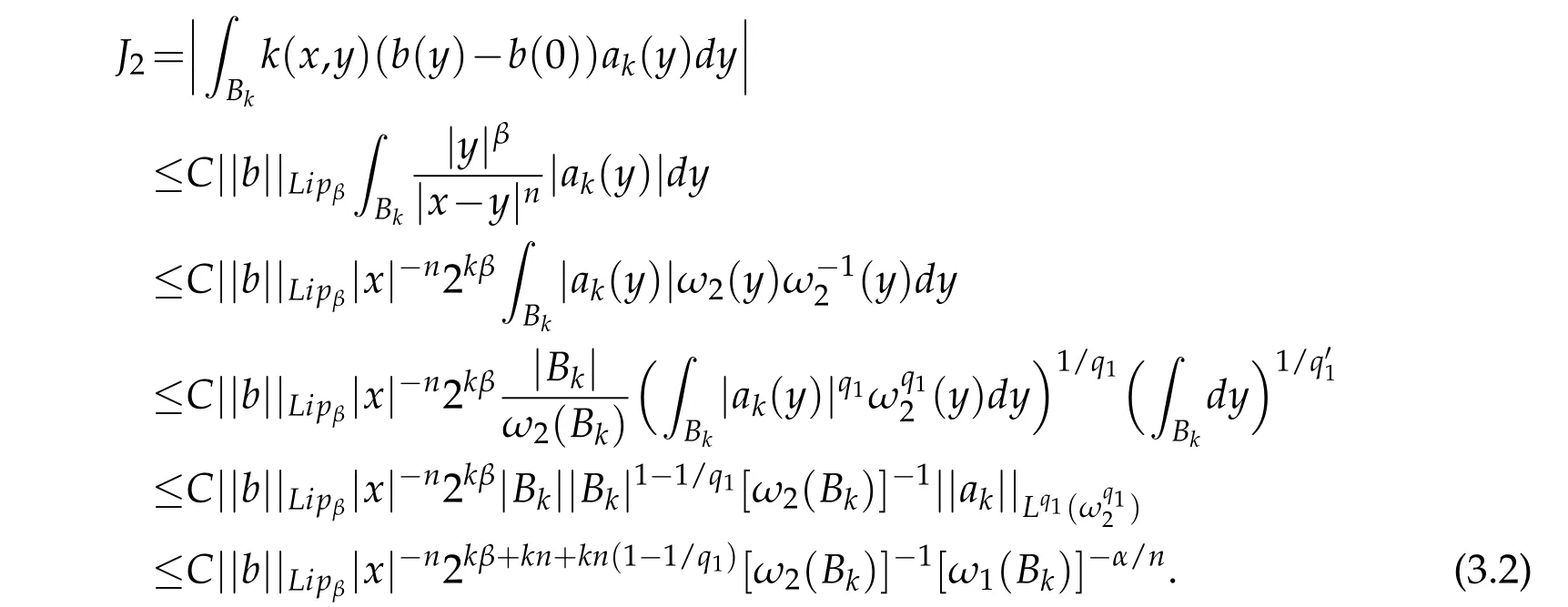
Applying the vanishing condition of a and Hölder's inequality,we get

In addition

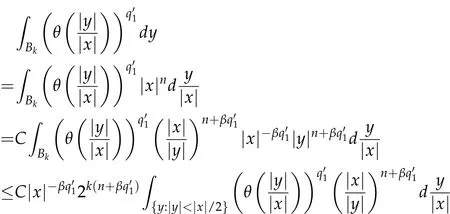
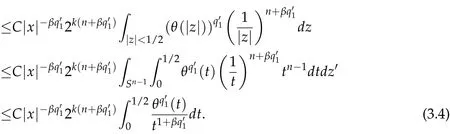
By Jensen's inequality,one can show that

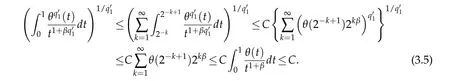
Combining(3.3),(3.4)with(3.5),we get

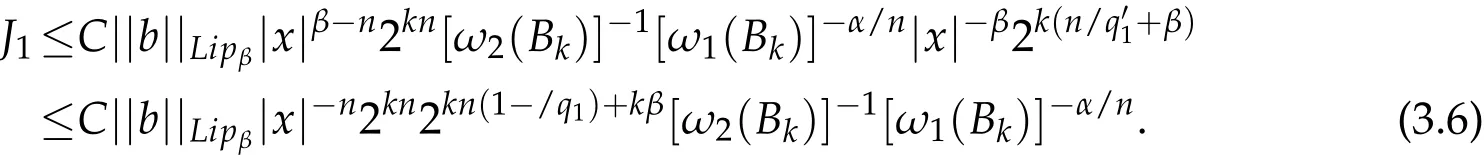
By(3.1),(3.2)and(3.6),we get

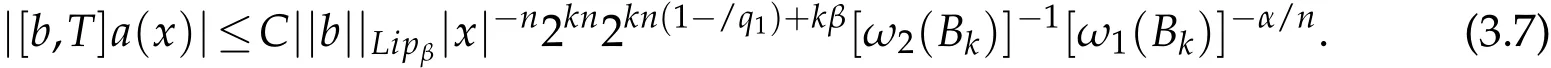
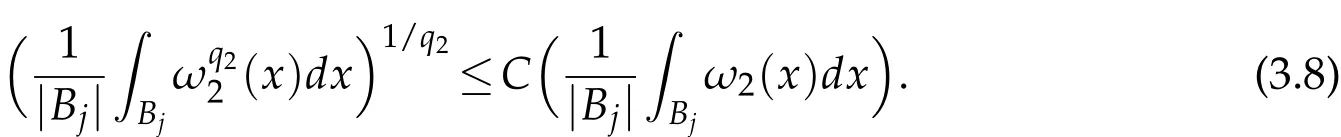
Thus,by(3.7),(3.8)and Lemma 3.2,we obtain

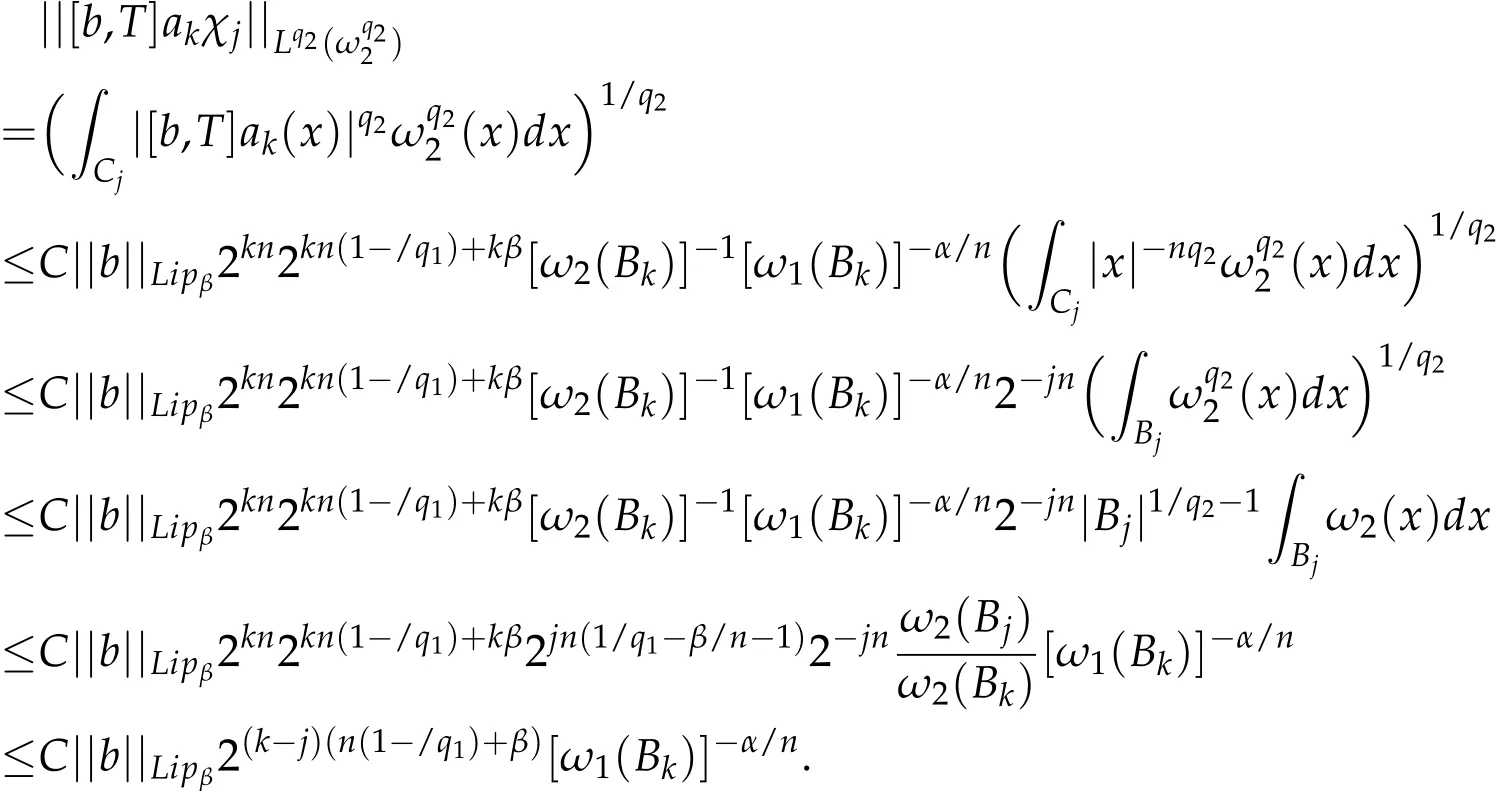
Similar to the estimate for II,we have

When 0＜p≤1,

If p＞1,by Hölder's inequality,we get

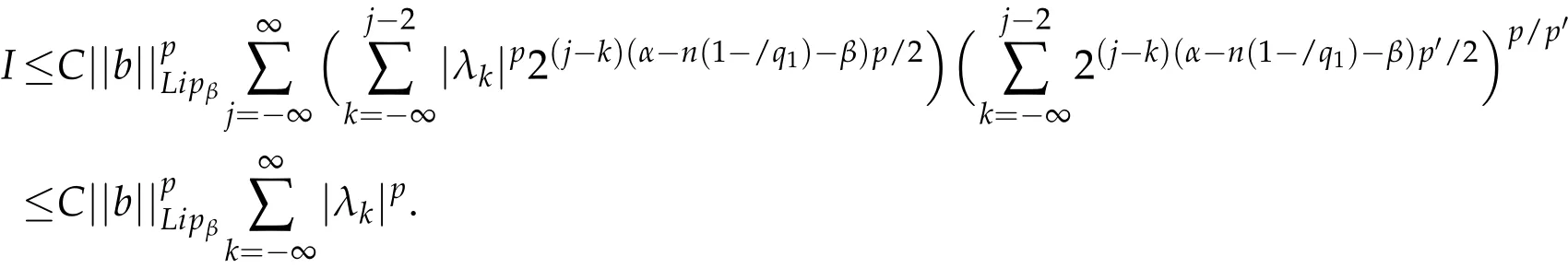
The estimates for I and II lead to

This completes the proof of Theorem 3.1.