Hopf Bifurcation of a Nonresident Computer Virus Model with Delay

Zizhen Zhang,Yougang Wangand Massimiliano Ferrara

1School of Management Science and Engineering,Anhui University of Finance and Economics,Bengbu 233030,Anhui,China

2Department of Law,Economics and Human Sciences,Mediterranea University of Reggio Calabria,Via dei Bianchi 2,89127 Reggio Calabria,Italy

Abstract.In this paper,a delayed nonresident computer virus model with graded infection rate is considered in which the following assumption is imposed:latent computers have lower infection ability than infectious computers.With the aid of the bifurcation theory,sufficient conditions for stability of the infected equilibrium of the model and existence of the Hopf bifurcation are established.In particular,explicit formulae which determine direction and stability of the Hopf bifurcation are derived by means of the normal form theory and the center manifold reduction for functional differential equations.Finally,a numerical example is given in order to show the feasibility of the obtained theoretical findings.

Key Words:Computer virus,delay,Hopf bifurcation,SLA model,Periodic solution.

1 Introduction

With the advance of software and hardware technologies,computer viruses have been a major threat to our daily life[1].It is an important matter to understand the spread law of computer viruses over the network.To achieve this goal,many dynamical models,such as SIR model[2],SIRS model[3-5],SEIR model[6],SEIRS model[7,8]and SEIQRS model[9,10]have been established by scholars at home and abroad to characterize the propagation of computer viruses.

Recently,the nonresident computer viruses that do not store or execute themselves from the computer memory have caused the attentions of many researchers[11].In order to analyze and protect against the nonresident computer viruses,Muroya and Kuniya proposed the following SLA computer virus model[12]:

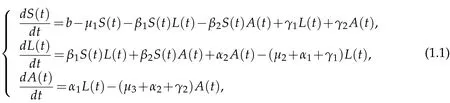
where S(t),L(t)and A(t)denote the numbers of uninfected computers,latent computers and infectious computers at time t,respectively;b is the number of external computers that are accessed to the network at time t;µ1,µ2and µ3are the rates at which the uninfected computers,latent computers and infectious computers are disconnected from the network;α1and α2are the rates of the nonresident computer viruses within latent computers are loaded into memory and nonresident computer viruses within infectious computers transfer control to the application program,respectively; β1and β2are the transmission rates of latent computers and infectious computers,respectively;γ1and γ2are the cure rates of latent computers and infectious computers,respectively.All the parameters in system(1.1)are positive constant.Muroya and Kuniya[12]investigated global stability and permanence of system(1.1).

However,studies on dynamical systems not only involve stability and permanence,but also involve some others such as bifurcation phenomenon and periodic solutions.Particularly,Hopf bifurcation of the dynamical systems with time delay are of considerable interest[13-16].Motivated by the work above and considering that the nonresident computer viruses within latent computers need a period to be loaded into memory,we consider the following system with time delay:

where τ1is the time delay due to the period that the nonresident computer viruses within latent computers need to be loaded into memory.

The subsequent materials of this paper are organized as follows.In Section 2,stability of the infected equilibrium and existence of Hopf bifurcation are discussed by analyzing the characteristic equation of system(1.2).The formulas for determining the properties of the Hopf bifurcation are derived by using the normal form method and center manifold theory.Then,a numericalexample is carried outto illustrate the validity of the theoretical results.Finally,conclusions are given in the last section.

2 Stability of the infected equilibrium and existence of Hopf bifurcation

Based on the analysis in[12]and by a direct computation,we know that if

then system(1.2)has a unique infected equilibrium E∗(S∗,L∗,A∗),where

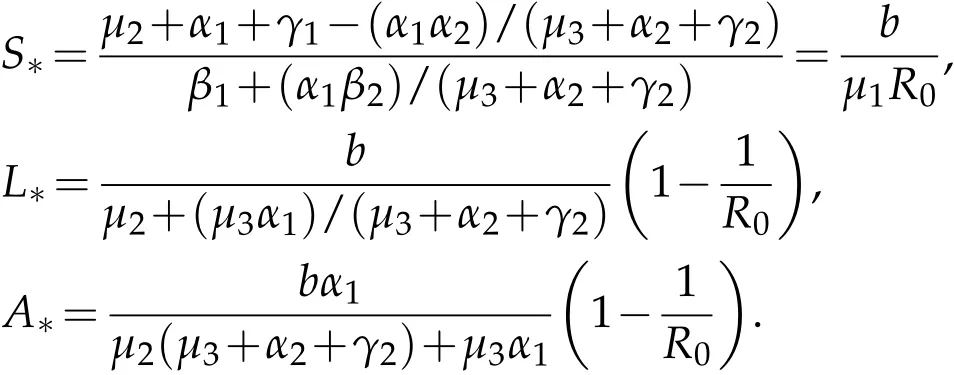
The Jacobian matrix of system(1.2)at the infected equilibrium E∗is

where

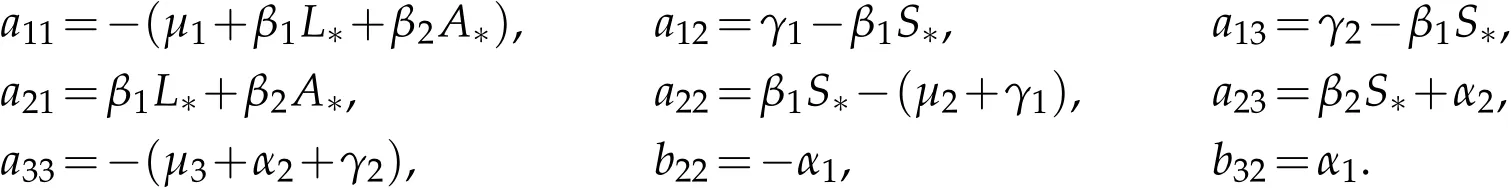
The characteristic equation is

where

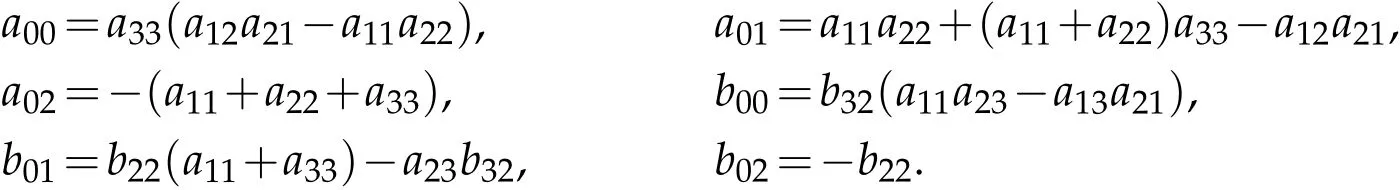
When τ=0,Eq.(2.1)reduces to

Thus,Routh-Hurwitz criterion implies that E∗is locally asymptotically stable without delay if the condition(H1)holds

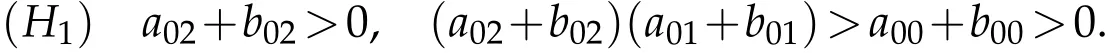
For τ＞0.Substituting λ=i ω(ω＞0)into Eq.(2.1)and separating the real and imaginary parts,we can obtain

It is easy to see from Eq.(2.3)that

where

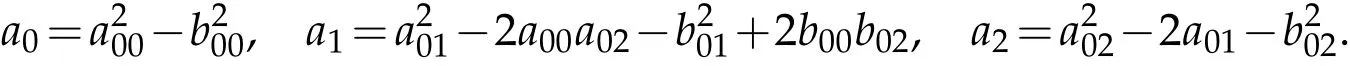
Let ω2=v,then

Define f(v)=v3+a2v2+a1v+a0.Song et al.[17]obtained the following results on the distribution of roots of Eq.(2.5).

Lemma 2.1.For the polynomial Eq.(2.5),

(1)if a0＜0,then Eq.(2.5)has at least one positive roots;

(2)if a0≥0 and Δ=-3a1≤0,then Eq.(2.5)has no positive roots;

(3)if a0≥0 and Δ=-3a1＞0,then Eq.(2.5)has positive roots if and only ifand f()≤0.

Next,we assume that the coefficients in Eq.(2.5)satisfy the following condition

Thus,Eq.(2.4)has at least one positive root such that Eq.(2.1)has a pair of purely imaginary roots ±iω0.The corresponding critical value τ0can be obtained from Eq.(2.3)

Taking derivative with respect to τ on both sides of Eq.(2.1),we obtain

Further,we have

Thus,if the condition(H3):holds,thenwhich implies that the transversality conditions is satisfied.From the discussions above and according to the Hopf bifurcation theorem in[18],we have the following.

Theorem 2.1.For system(1.2),if the conditions(H1)-(H3)hold,then the infected equilibrium E∗(S∗,L∗,A∗)of system(1.2)is locally asymptotically stable for τ ∈ [0,τ0)and system(1.2)undergoes a Hopf bifurcation at the positive equilibrium E∗(S∗,L∗,A∗)when τ =τ0,where τ0is defined in Eq.(2.6).

3 Direction and stability of the Hopf bifurcation

Let u1(t)=S(t)-S∗,u2(t)=L(t)-L∗,u3(t)=A(t)-A∗,τ=τ0+µ,µ∈R.Then,wecanknow thatµ=0 is the Hopf bifurcation value for system(1.2).Rescale the time by t→(t/τ)to normalize the time delay so that system(1.2)can be rewritten as

where ut=(u1(t),u2(t),u3(t))T∈C=C([-1,0],R3),

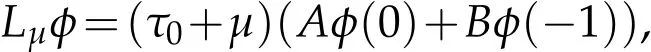
and

where

AAccording to the representation theorem, there exists a 3×3 matrix function with bounded variation components η(θ,µ),θ∈[-1,0]such that

In fact,we choose

where δ is the Dirac delta function.

For φ∈C([-1,0],R3),define

and

Then system(3.1)is equivalent to

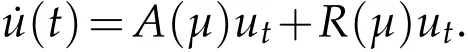
For ϕ ∈C1([0,1]),(R3)∗,the adjoint operator A∗of A is defined as

and a bilinear inner product is defined by

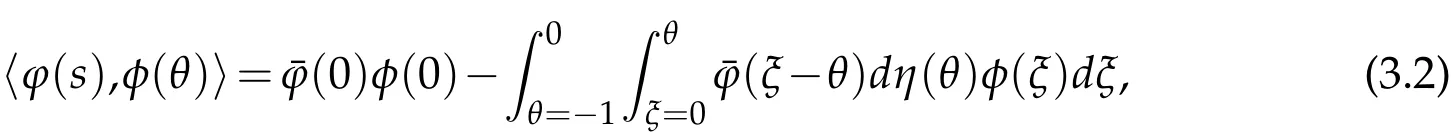
where η(θ)=η(θ,0).

Let q(θ)=(1,q2,q3)Teiω0τ0θbe the eigenvector of A(0)belonging to+iω0τ0and q∗(s)=D(1,,)eiω0τ0sbe the eigenvector of A∗(0)belonging to-iω0τ0.By a direct computation,we can get

From Eq.(3.2),we can get

Then we choose

such that〈q∗,q〉=1.

Next,we can obtain the coefficients by using the method introduced in[18]and a computation process similar as that in[13]:

with

where E1and E2are given by the following equations,respectively

Then,we can get the following coefficients which determine the properties of the Hopf bifurcation:

In conclusion,we have the following results.

Theorem 3.1.For system(1.2),Ifµ2＞0(µ2＜0),then the Hopf bifurcation is supercritical(subcritical).If β2＜0(β2＞0),then the bifurcating periodic solutions are stable(unstable).If T2＞0(T2＜00),then the bifurcating periodic solutions increase(decrease).

4 Numerical simulation

In order to verify the analytical predictions obtained in our paper,we present some numerical simulations in this section.By extracting some values from[12]and taking the conditions for the existence of the Hopf bifurcation into account,we consider the following special case of system(1.2)with the parameters b=10,α1=4,α2=1.5,β1=1,β2=2.5,γ1=0.25,γ2=0.75,µ1=1,µ2=1.5,µ3=2.Then,we get the following system:

By means of Matlab 7.0,we get R0=7.7288 and that system(4.1)has a unique infected equilibrium E∗(1.2939,2.5740,2.4226).Then,wehave a00+b00=163.6174,a01+b01=92.8527,a02+b02=18.3366.Obviously,The condition(H1)is satisfied for system(4.1).Further,we can validate that the condition(H2)is satisfied and we can obtain ω0=0.9623,τ0=1.8150 and f′()=152.6377＞0.That is,the condition(H3)holds.Thus,according to Lemma 2.1,we can conclude that E∗(1.2939,2.5740,2.4226)is locally asymptotically stable when τ ∈ [0,τ0=1.8150).However,when the time delay passes through τ0,E∗(1.2939,2.5740,2.4226)loses its stability and a Hopf bifurcation occurs and a family of periodic solutions bifurcate from E∗(1.2939,2.5740,2.4226).The bifurcation phenomenon of system(4.1)can be illustrated by the computer simulation in Fig.1.

5 Conclusions

In this paper,a delayed nonresident computer virus model is investigated by incorporating the time delay due to the period used to load the nonresident virus within latent computers into memory into the SLA model proposed in[12].Compared with the conventional computer virus models such as SIRS model[3-5],the SEIRS model[7,8]and SEIQRS model[9,10],we not only consider the infection ability of the infective computers but also the infection ability of the latent computers.That is,the model considered in this paper is more realistic.On the other hand,the main purpose of this paper is to investigate the effect of the time delay on the model compared with the work in[12].

Figure 1:The bifurcation diagram with respect to τ.

It is found that,under moderate conditions,the infected equilibrium of the model is locally asymptotically stable when the value of the delay is suitable small(τ ＜ τ0),which implies that propagation of the computer virus can be predicted and controlled effectively.However,a Hopf bifurcation emerges when the delay passes through the critical value τ0.This means that the state of the computer virus prevalence changes from the infected equilibrium to a limit cycle.Namely,the propagation of the computer virus is out of control.Therefore,we can conclude that we should take some measures to postpone the occurrence of the Hopf bifurcation in order to control the propagation of the computer virus.From the numerical simulation,we find that onset of the Hopf bifurcation can be delayed if the values of the parameter γ1and γ2increase,which can be realized by means of strengthening the immunization of the new computers connected to the network.Thus,we can conclude that the managers of the network should strengthen the immunization of the new computers connected to the network so as to predict and control the propagation of the computer virus in the network easily.Furthermore,the properties of the Hopf bifurcation have also been investigated in the paper.

Acknowledgements

The author would like to thank the editor and the anonymous referees for their valuable comments and suggestions on the paper.This work was supported by Natural Science Foundation of Anhui Province(Nos.1608085QF145,1608085QF151)and Project of Support Program for Excellent Youth Talent in Colleges and Universities of Anhui Province(No.gxyqZD2018044).