Erdös Type Inequality for Lorentz Polynomials

Laiyi Zhu,Dapeng Zhouand Zhiyong Huang

School of Mathematics,Renmin University of China,Beijing 100872,China

Abstract.An elementary,but very useful tool for proving inequalities for polynomials with restricted zeros is the Bernstein or Lorentz representation of polynomials.In the present paper,we give two classes of Lorentz polynomials,for which the Erdös-type inequality holds.

Key Words:Lorentz representation of polynomials,constrained polynomials,Morkov-type inequalities,Erdös-type inequality.

1 Introduction and main results

Let πndenote the set of all polynomials of degree at most n with real coefficients,and πcndenote the set of all polynomials of degree at most n with complex coefficients,where n is a nonnegative integer.

Let

denote the supremum norm of a function f defined on a set A.The Markov inequality is that

holds for all pn∈.And the Bernstein inequality is that

holds for all pn∈and for all x∈(-1,1).For proofs of these see[2]or[3].Polynomial inequalities are very basic in several disciplines and they play a foundational role in approximation theory.There are a lot of papers devoted to them;see,e.g.,[2]and[11].In[7],Erdös gave a class of restricted polynomials for which the Markov factor n2in(1.1)improves to cn.He proved the following theorem.

Theorem 1.1.The inequality

holds for all pn∈πnhaving all their zeros in R(-1,1).

And in[7],Erdös claimed the following theorem but did not give a hint to prove it.Recently,Erdélyi proved it in[5].Using different approach,We gave another proof of Theorem E2in[14].

Theorem 1.2.The inequality

holds for all pn∈πnhaving all their zeros in R(-1,1)and

These results motivated several people to study Markov- and Bernstein-type inequalitiesfor polynomials with restricted zeros and under some other constraints. These peopleinclude Lorentz[8],Scheick[12],Szabados[13],Máté[10],P.Borwein[1],Erdélyi[4,5]and others.

An elementary,but very useful tool for proving inequalities for polynomials with restricted zeros is the Bernstein or Lorentz representation of polynomials;see,e.g.,[2]and[6].

Let

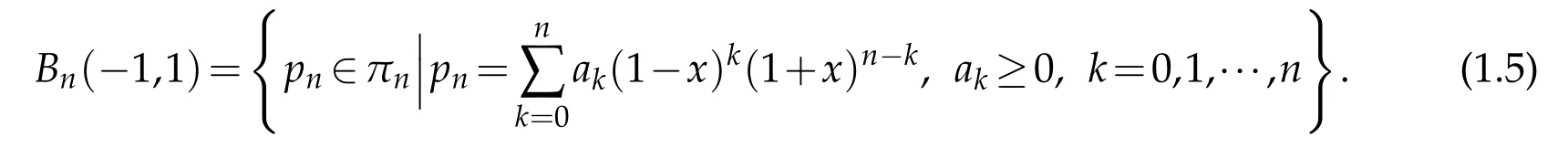
And if pn(x)∈Bn(-1,1)or-pn(x)∈Bn(-1,1),we call it Lorentz polynomial.As Lorentz observed that,if pn(x)∈πnhaving all their zeros outside the open unit disk,then pn(x)is a Lorentz polynomial.

In this paper,we give two classes of Lorentz polynomials,for which the Erdös-type inequality(1.4)holds.Our main results are the following.

Theorem 1.3.Let n≥1 be an integer and pn(x)∈πnπn-1be a Lorentz polynomial.If,then

Equality holds only for pn(x)=σc(1+σx)nor pn(x)=σc[2n-(1-σx)n]withaconstant0≠c∈R and σ∈{-1,1}.

Theorem 1.4.Let n≥3 be an integer and pn(x)∈πnπn-1be a Lorentz polynomial with Lorentz polynomial representation

then

Moreover,if

then equality holds only for pn(x)=c1(1+x)n-2[(1+x)2+c2(1-x)2]with constants c1＞0 and 0≤c2≤1.

2 Some lemmas

In order to prove our main results,we need the following lemmas.The first one is the well known Lucas'theorem(to see[9]or[2]).

The next lemma is a result ascribed to Lorentz,to see[2]or[5].

Lemma 2.2.Suppose p∈πnhas its zeros outside the open unit disk,then pn(z)is a Lorentz polynomial.

To look at the conditions for a Lorentz polynomial pn(x)∈πn,we have the following two lemmas.

Lemma 2.3.Let n≥1 be an integer and pn(x)∈πn.For a Lorentz polynomial

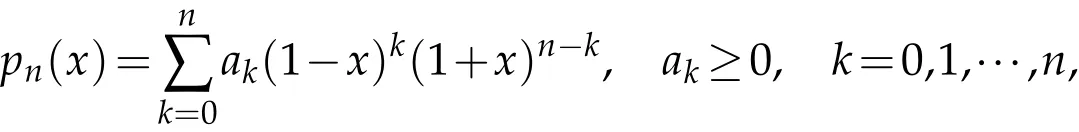
or

Proof.This follows from the simple calculations

So,we complete the proof.

From(2.1)and(2.2),we obtain immediately the following lemma.

Lemma 2.4.Let n≥1 be an integer and pn(x)∈πn.For a Lorentz polynomial

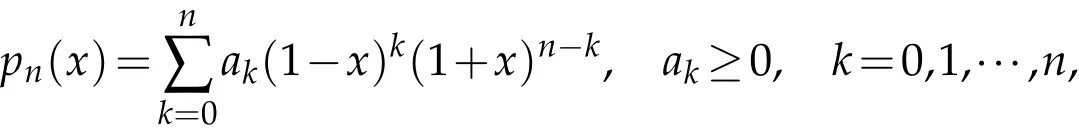
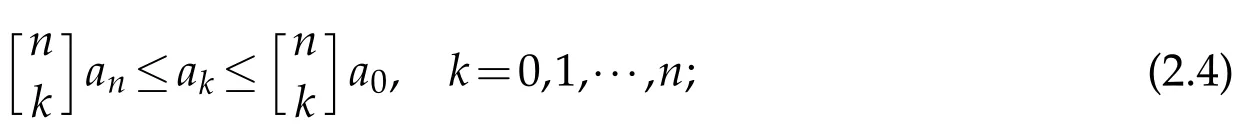
moreover,if a0=an,thenholds if and only if

3 Proofs of the main results

Proof of Theorem 1.3.Let pn∈πnπn-1be a Lorentz polynomial.Without loss of generality we may assume that

Thus,(2.3)and(2.4)imply that for all x∈[-1,1],

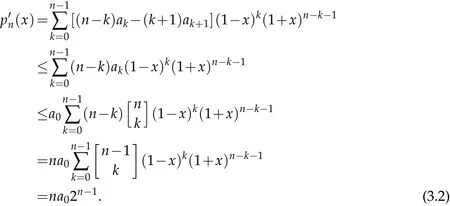
So that

and for all x∈[-1,1],

Hence

For the case that equality holds,without loss of generality,we may assume that there exists an x0∈[-1,1]such that

Then(3.2),yields x0=1 or x0=-1.If x0=1,then it is from(2.3)that na0-a1=na0,which implies

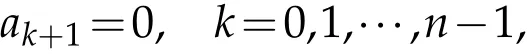
hence

If x0=-1,then it is from(2.3)that an-1-nan=na0.From(2.1),we can deduce that an=0 and

So

from which it follows that

and the Theorem is proved.

Remark 3.1.(a)If pn∈πnhas all its zeros in R(-1,1)and(x)≠0,x∈(-1,1),then it is from Lemma 2.2 that pn∈πnπn-1is a Lorentz polynomial and pn(x)∈Bn(-1,1)or-pn(x)∈Bn(-1,1).The following example shows that Theorem 1.3 extends essentially Theorem 1.2.

Example 3.1.Let m≥1 be an integer.Then for

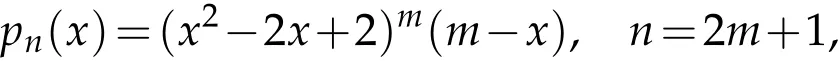
with all its zeros at x=1±i and x=m.It follows from Lemma 2.1 that p(k)(x),k=1,2,···,n-1,have all their zeros in the triangle formed by x=1±i and x=m which are certainly outside the open unit disk.Hence from Lemma 2.2,pn(x)∈πnπn-1is a Lorentz polynomial and-(x)∈ Bn-1(-1,1).By simple calculations,we get

and

Remark 3.2.(b)There is an alternative proof of(1.6).In fact,suppose pn(x)∈Bn(-1,1)andThen it follows from Lemma 2.3 and Lemma 2.4(or even by one's geometric intuition)that

Applying Theorem 2.3 in[5]with Qn(x),we obtain

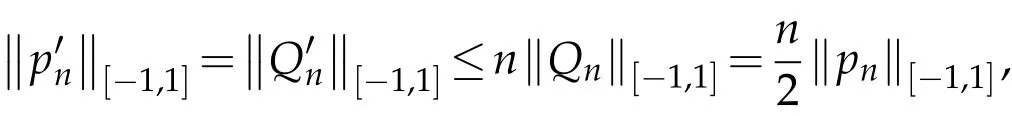
which gives the alternative proof of(1.6).

We emphasize here that the methods we used to deduce(1.6)is innovative and quiet different from T.Erdélyi's.We provide a direct and concise elementary proof to Theorem 1.3 using only undergraduate calculus.

Proof of Theorem 1.4.Let n≥3be an integerand pn(x)∈πnπn-1with Lorentz polynomialrepresentation

It follows from(1.7)and(2.3)that for x∈[-1,1]

Moreover,if

Then(3.7)implies x0=1 or x0=-1.If x0=1,then it is from(2.3)that na0-a1=na0.So(1.8)deduce that

and

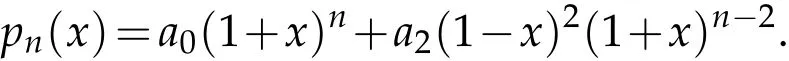
If x0=-1,then it is from(2.3)that an-1-nan=na0.However,(1.8)implies an-1≤a0,so nan+na0≤a0,a contradiction,which finishes the proof. ?

Remark 3.3.(a).By the transformation t=-x,we obtain the following result:Let n≥3 be an integer and pn(x)∈πnπn-1be a Lorentz polynomial with Lorentz polynomial representation

then

Moreover,if

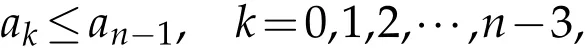
then equality holds only for pn(x)=c1(1-x)n-2[(1-x)2+c2(1+x)2]with constants c1＞0 and 0≤c2≤1.

(b).The following example satisfies the conditions of Theorem 1.4,which also shows that the assumption ”(x)∈ Bn-1(-1,1)or-(x)∈ Bn-1(-1,1)” is not necessary for Lorentz polynomial pn(x)to satisfy the Erdös inequality,and the necessary conditions for a Lorentz polynomial pn(x)to satisfy the Erdös inequality remain to be solved.

Example 3.2.Let n≥3 be an integer.Consider Lorentz polynomial

Then

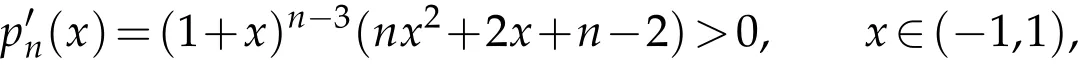
then

Acknowledgements

The research has been supported by the National Natural Science Foundation of China under Grant No.11571362.The authors would like to thank the referee for useful comments and suggestions which improved the presentation of this paper.