Domain of Euler Mean in the Space of Absolutely p-Summable Double Sequences with 0＜p＜1

Medine Yes¸ilkayagiland Feyzi Bas¸ar

1School of Applied Sciences,U¸sak University,1 Eylül Campus,64200-U¸sak,Turkey

2Professor Emeritus, Faculty of Education, Inönü University, Malatya 44280, Turkey

Abstract.In this study,as the domain of four dimensional Euler mean E(r,s)of orders r,s in the space Lpfor 0＜p＜1,we examine the double sequence space Er,spand some properties of four dimensional Euler mean.We determine the α-and β(bp)-duals of the space Er,sp,and characterize the classes(Er,sp:Mu),(Er,sp:Cbp)and(Er,sp:Lq)of four dimensional matrix transformations,where 1≤q＜∞.Finally,we shortly emphasize on the Euler spaces of single and double sequences,and note some further suggestions.

Key Words:Summability theory,double sequences,double series,alpha-,beta-and gammaduals,matrix domain of 4-dimensional matrices,matrix transformations.

1 Introduction

We denote the set of all complex valued double sequences by Ω which is a vector space with coordinatewise addition and scalar multiplication.Any vector subspace of Ω is called as a double sequence space.A double sequence x=(xmn)of complex numbers is said to be bounded ifkxk∞=supm,n∈N|xmn|＜ ∞,where N={0,1,2,···}.The space of all bounded double sequences is denoted by Muwhich is a Banach space with the norm k·k∞.Consider the sequence x=(xmn)∈Ω.If for every ε＞0 there exists n0=n0(ε)∈N and l∈C such that|xmn-l|＜ε for all m,n＞n0,then we call that the double sequence x is convergent in the Pringsheim's sense to the limit l and write p-limm,n→∞xmn=l;where C denotes the complex field.By Cp,we denote the space of all convergent double sequences in the Pringsheim's sense.It is well-known that there are such sequences in the space Cpbut not in the space Mu.Indeed following Boos[7,pp.16],if we define the sequence x=(xmn)by

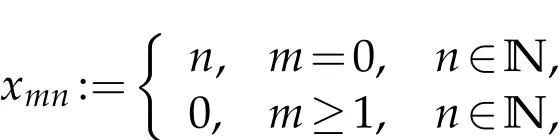
then it is trivial that x∈Cp-Mu,since p-limm,n→∞xmn=0 butkxk∞=∞.So,we can consider the space Cbpof the double sequences which are both convergent in the Pringsheim's sense and bounded,i.e.,Cbp=Cp∩Mu.A sequence in the space Cpis said to be regularly convergent if it is a single convergent sequence with respect to each index and denote the space of all such sequences by Cr.Also by Cbp0and Cr0,we denote the spaces of all double sequences converging to 0 contained in the sequence spaces Cbpand Cr,respectively.Móricz[12]proved that Cbp,Cbp0,Crand Cr0are Banach spaces with the norm k·k∞.

Let λ be a space of double sequences,converging with respect to some linear convergence rule ϑ-lim:λ→C.The sum of a double series∑i,jxijwith respect to this rule is defined byFor short,throughout the text the summations without limits run from 0 to∞,for example∑i,jxijmeans that

The α-dual λα,β(ϑ)-dual λβ(ϑ)with respect to the ϑ-convergence and the γ-dual λγof a double sequence space λ are respectively defined by

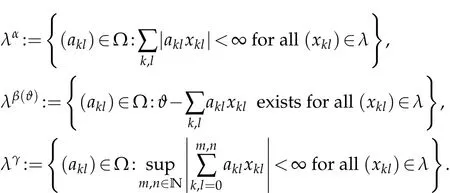
It is easy to see for any two spaces λ,µ of double sequences thatµα⊂ λαwhenever λ⊂µ and λα⊂λγ.Additionally,it is known that the inclusion λα⊂λβ(ϑ)holds while the inclusion λβ(ϑ)⊂λγdoes not hold,since the ϑ-convergence of a sequence of partial sums of a double series does not imply its boundedness.

Let λ and µ be two double sequence spaces,and A=(amnkl)be any four-dimensional complex in finite matrix.Then,we say that A defines a matrix mapping from λ into µ and we write A:λ→µ,if for every sequence x=(xkl)∈λ the A-transform Ax={(Ax)mn}m,n∈Nof x exists and is inµ;where

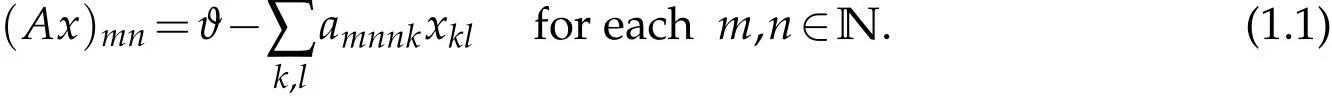
We define the ϑ-summability domainof A in a space λ of double sequences by

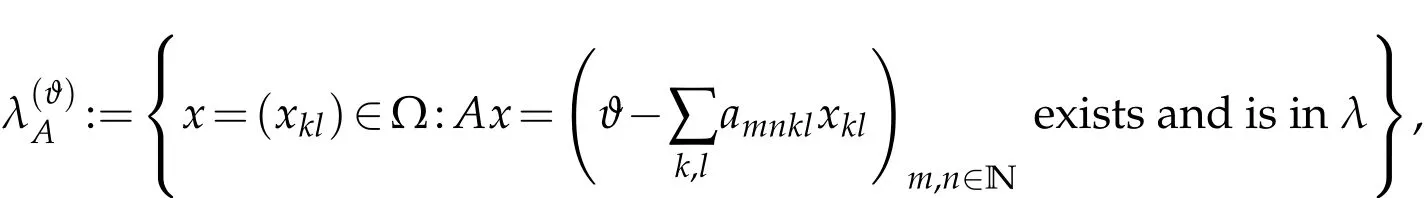
where ϑ denotes any of the symbols p,bp or r.

We say with the notation(1.1)that A maps the space λ into the space µ ifand we denote the set of all four dimensional matrices,transforming the space λ into the space µ,by(λ:µ).Thus,A=(amnkl)∈(λ:µ)if and only if the double series on the right side of(1.1)converges in the sense of ϑ for each m,n∈N,i.e.,Amn∈λβ(ϑ)for all m,n∈N and every x∈λ,and we have Ax∈µ for all x∈λ;where Amn=(amnkl)k,l∈Nfor all m,n∈N.In this paper,we only consider bp-summability domain.

For all m,n,k,l∈N,we say that A=(amnkl)is a triangular matrix if amnkl=0 for k＞m or l＞n or both,[1].By following Adams[1],we also say that a triangular matrix A=(amnkl)is called a triangle if amnmn≠0 for all m,n∈N.Referring to Cooke[8,Remark(a),pp.22],onecan conclude that every triangle matrixhas an unique inverse which is alsoa triangle.

Zeltser[23]studied both the theory of topological double sequence spaces and the theory of summability of double sequences in her PhD thesis.Altay and Bas¸ar[2]defined the spaces BS,BS(t),CSp,CSbp,CSrand BV of double series whose sequence of partial sums are in the spaces Mu,Mu(t),Cp,Cbp,Crand Lu,respectively.Bas¸ar and Sever[6]introduced the space Lpof double sequences as

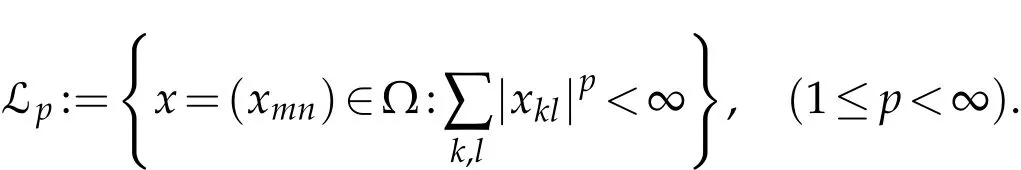
The space Lphas been recently used by the papers Mursaleen and Bas¸ar[13],Demiriz and Duyar[10],C¸apan and Bas¸ar[9]and Yes¸ilkayagil and Bas¸ar[22].

The reader can refer to Bas¸ar[5]and Mursaleen and Mohiuddine[15]for relevant terminology and required details on the double sequences and related topics.

Let 0＜r,s＜1.The Euler mean of orders r and s for double sequences defined by the four dimensional matrixas follows

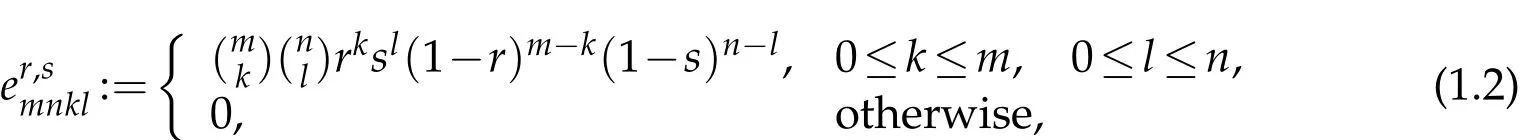
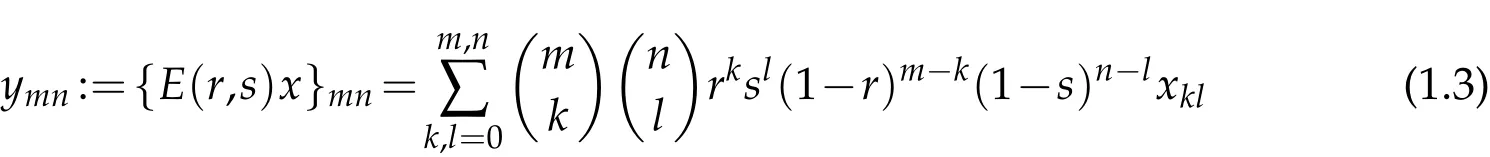
for all m,n,k,l∈N.Therefore,the E(r,s)-transform of a double sequence x=(xmn)is given by for all m,n∈N.Throughout the paper,we suppose that the terms of the double sequences x=(xmn)and y=(ymn)are connected with the relation(1.3),and we assume unless stated otherwise that 0＜r,s＜1 and 0＜p＜1.

Let I=(δmnkl)be four dimensional unit matrix,that is,

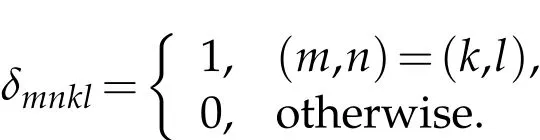
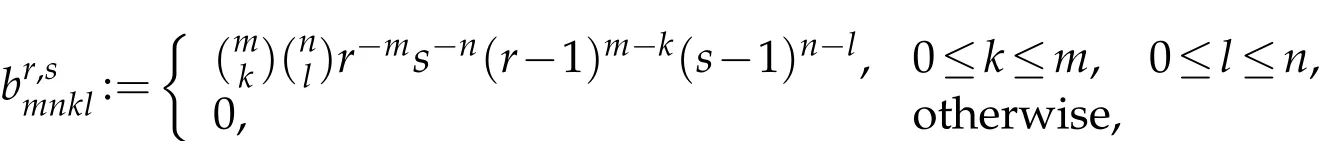
for all m,n,k,l∈N.

In 1953,Wollan[21]introduced the Euler summability of double series.Nuray and Patterson[16]have studied the four dimensional summability methods of Euler and Borel as mappings from absolutely summable double sequences into themselves and they have given two Tauberian theorems for these summability methods.

In the present paper,following Talebi[19]we examine the spaceas the set of all sequences whose E(r,s)-transforms are in the space Lp,that is,

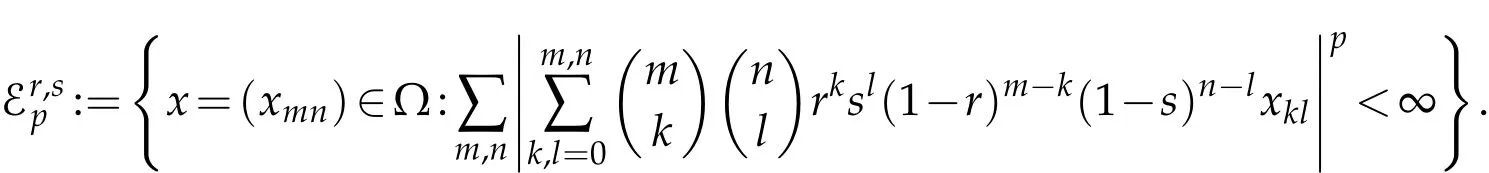
The rest of this paper is organized,as follows:In the section titled Main Results,we give some properties of four dimensional Euler mean E(r,s)of orders r,s and introduce the spaceas the domain of E(r,s)in the space Lp.Additionally,we determine the α-and β(bp)-dual of the space and characterize the classes of linear operators represented by the four dimensional matrices from the spaceinto the spaces Mu,Cbpand Lq;where 1≤q＜∞.In the final section of the paper,we summarize the literature related to the domains of two and four dimensional Euler means in the spaces ‘∞,c,c0,‘pand Lp,and record some further suggestions.

2 Main results

2.1 Some properties of four dimensional Euler mean

In this subsection,we show the regularity and examine some properties of the Euler mean E(r,s)of orders r,s.

Definition 2.1(see[11,18]).A four dimensional matrix A is said to be RH-regular if it maps every bounded p-convergent sequence into a p-convergent sequence with the same p-limit.

Lemma 2.2(see[11,18]).A four dimensional triangle matrix A=(amnkl)is RH-regular if and only if

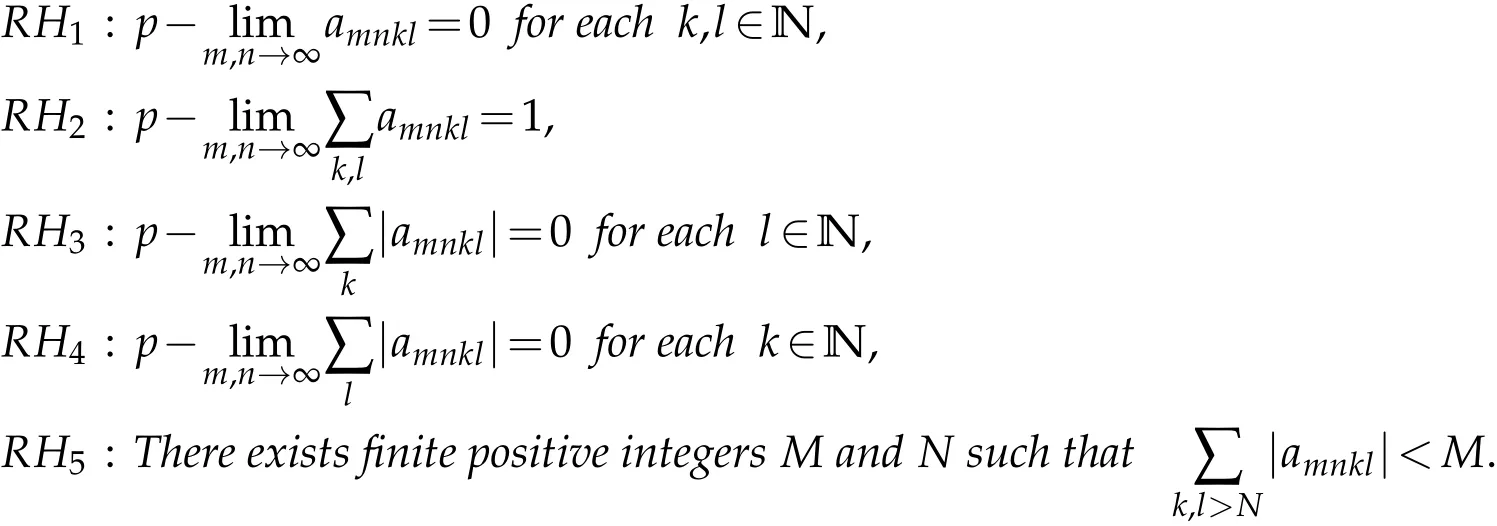
Theorem 2.3.The four dimensional Euler matrix E(r,s)of orders r,s,defined by(1.2)is RH-regular.

Proof.Since

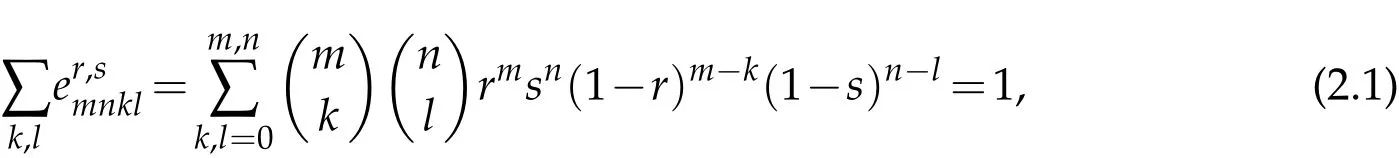
we have that p-limm,n→∞=1,that is,RH2holds.Using the relation(2.1)and positivity of the matrix E(r,s),i.e.,≥0 for all m,n,k,l∈N,one can see that the condition RH5is satisfied.Since(1-r)m-k→0,as m→∞ and(1-s)n-l→0,as n→∞for 0＜r,s＜1(see[17,pp.57]),we have that→0,as m,n→∞ for each k,l∈N,that is,RH1is satisfied.With the similar way,the conditions RH3and RH4also hold.This completes the proof.

Theorem 2.4.E(r,s)E(z,t)=E(rz,st)holds for all r,s,z,t∈R.

Proof.Let x=(xkl)∈Ω.Sinceandfor all i,j,k,l,m,n∈N,we obtain that

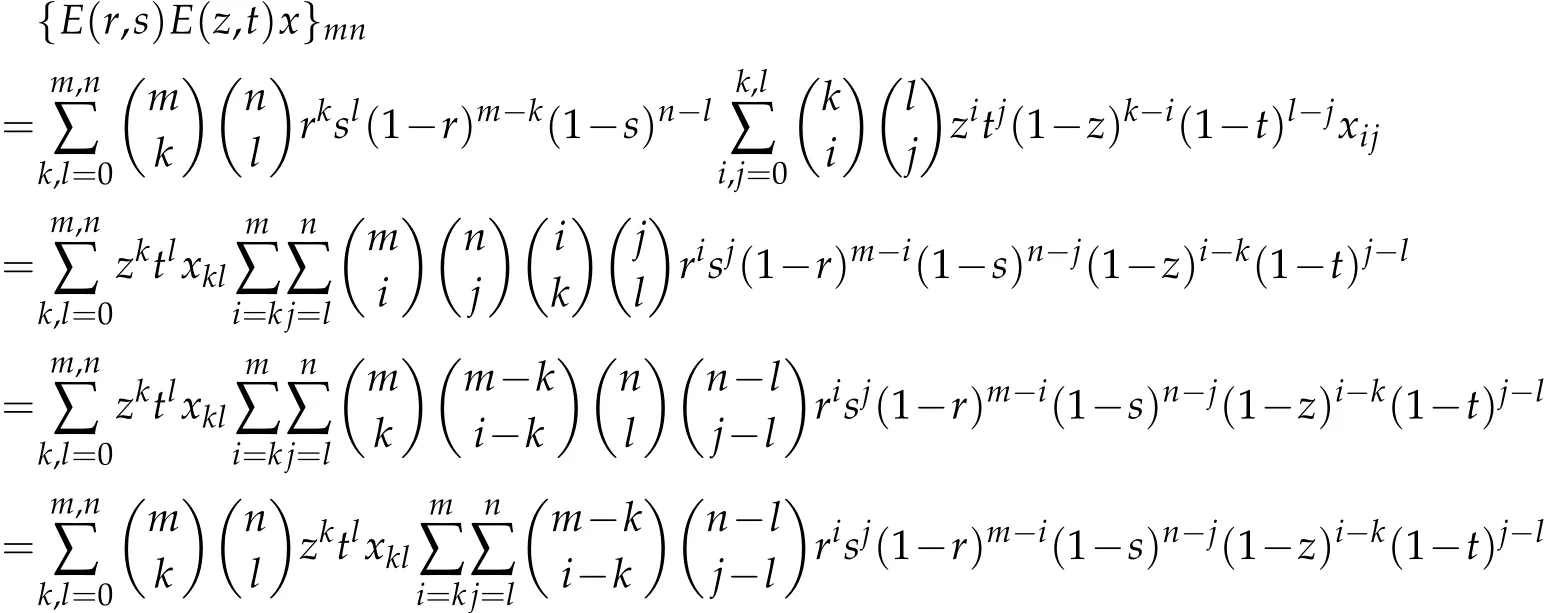
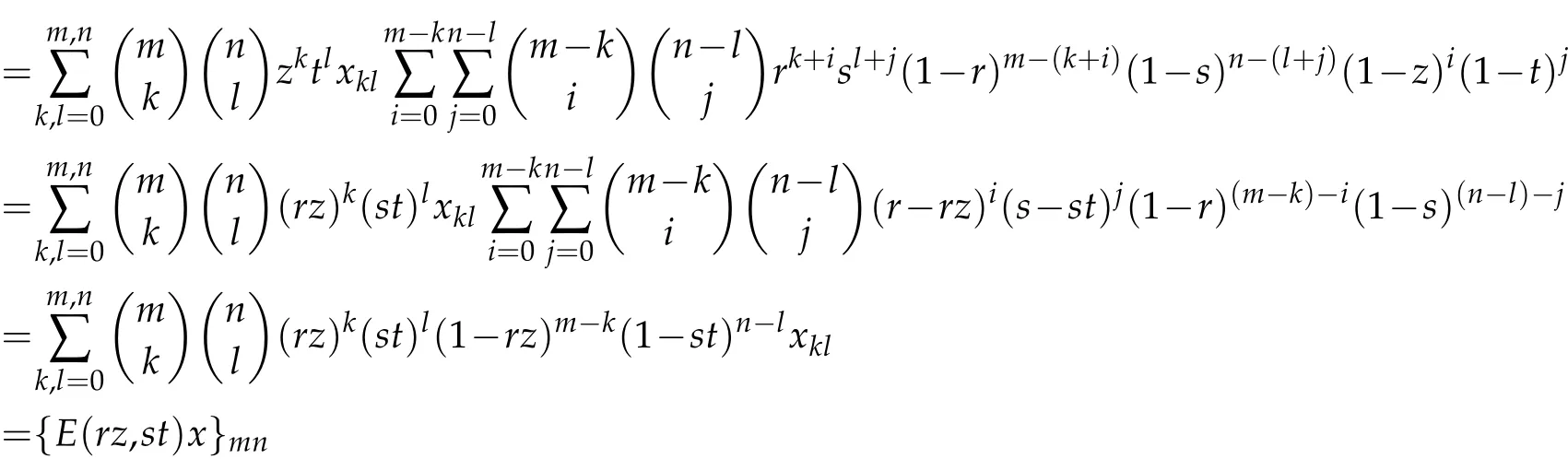
for each m,n∈N.

This completes the proof.

Theorem 2.5.Let E(r1,s1)=()and E(r2,s2)=()be four dimensional Euler matrices of orders r1,s1and r2,s2,respectively,and define the four dimensional matrix C=()by

for all m,n,k,l∈N,where 0＜r1,r2,r3,s1,s2,s3＜1.Then,the matrix C is an Euler matrix.

Suppose that the matrix C is not an Euler matrix for all m,n,k,l∈N and 0＜r3,s3＜1.Taking m=k-1 and n=l-1 and using the factsandfor all m,n∈N,we solve the equality(2.2).

If we take 0＜r3=r1r2＜1 and 0＜s3=s1s2＜1,we have

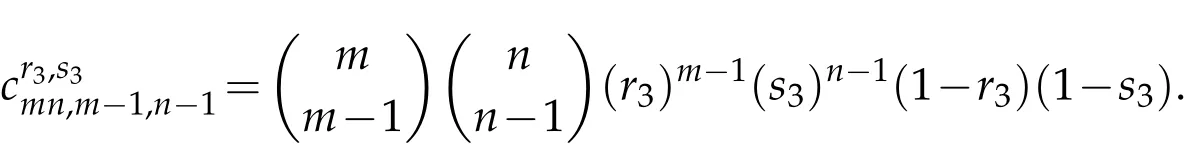
Since m,n∈N are arbitrarily,we have a contradiction.So,the proof is completed.

Corollary 2.6.If the four dimensional Euler matrices E(r1,s1)and E(r2,s2)are RH-regular,then the product E(r1,s1)E(r2,s2)is also RH-regular.

Theorem 2.7.Let 0＜r′＜r＜1 and 0＜s′＜s＜1,and x∈Cbp.If p-limm,n{E(r,s)x}mn=α,then p-limm,n{E(r′,s′)x}mn=α.

Proof.Let p-limm,n{E(r,s)x}mn=α for all x∈Cbp,0＜r′＜r＜1 and 0＜s′＜s＜1.Then there are ε1,ε2＞0 such that ε1r=r′and ε2s=s′.So,0＜ ε1,ε2＜1.Therefore,we have by Theorem 2.4 that

Since x∈Cbp⊂Mu,it is immediate that

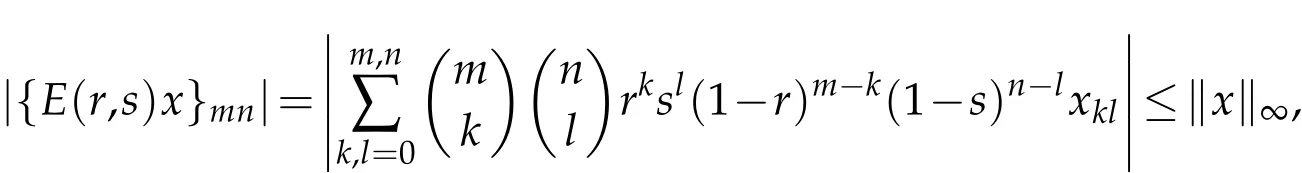
that is,E(r,s)x∈Cbpwith p-limit α.Again,since E(ε1,ε2)is RH-regular,

So,by(2.3)we have p-limm,n{E(r′,s′)x}mn=α,as desired.

With the notation of Zeltser[24],we define the double sequencesby

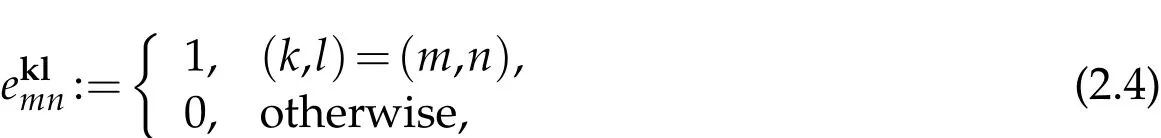
for all k,l,m,n∈N.A non-empty subset S of a locally convex space X is called fundamental if the closure of the linear span of S equals X,[7].Using this definition,Yes¸ilkayagil and Bas¸ar[22]have showed that S is the fundamental set of Lp,where S:={ekl:k,l∈ N}.In the light of this fact,we define the double sequencesby

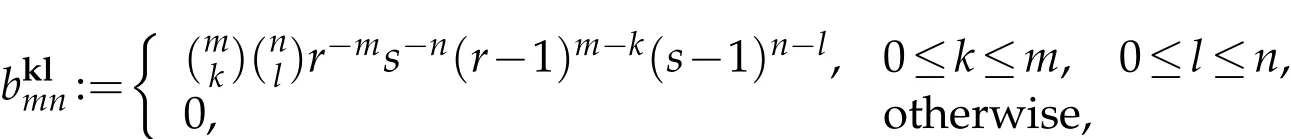
for all k,l,m,n∈N.Then,{bkl:k,l∈N}is the fundamental set of the space;since E(r,s)bkl=ekl.

2.2 The space of double sequences

In this subsection,we introduce the spaceof double sequences.Also,one can find the following Theorem and Remark in[20].

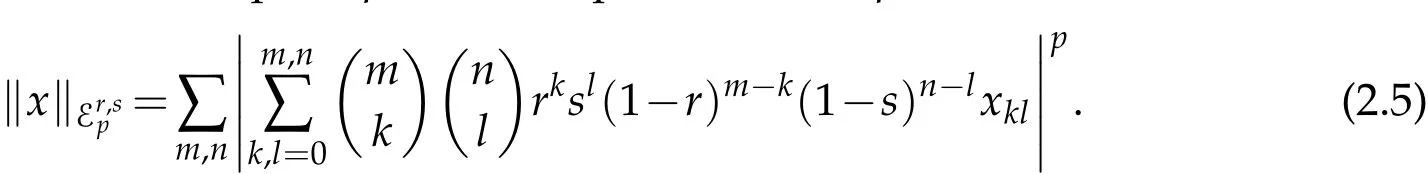
Remark 2.9.Let T be the transformation fromto Lpdefined by x7→Tx=E(r,s)x.Then,since the transformation T is bijective the spaceis linearly p-norm isomorphic to the space Lp.

2.3 The β(bp)-,α-and γ-duals of the space

In this subsection,we determine the α-and the β(bp)-duals of the space.

Lemma 2.10.Let A=(amnkl)be any four dimensional matrix.Then,the following statements are satisfied:

(i)In[22,Theorem 4.1]A∈(Lp:Mu)if and only if

(ii)In[22,Theorem 4.2]A=(amnkl)∈(Lp:Lq)if and only if

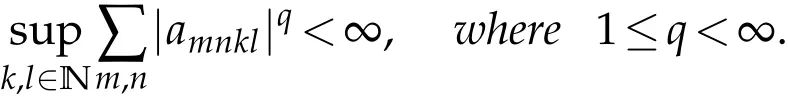
(iii)In[22,Theorem 4.3]A∈(Lp:Cbp)if and only if(2.6)holds and there exists(αkl)∈Ω such that

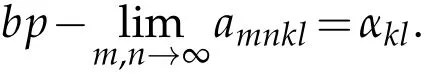
Theorem 2.11.Define the sets d1,d2and d3,as follows:

Proof.Let x=(xmn)∈.Then,Remark 2.9 implies that there exists a double sequence y=(ymn)∈Lp.Define the four-dimensional matrix B=(bmnkl)by

for all m,n,k,l∈N.Therefore,we obtain by the relation(1.3)that

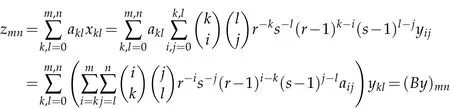
for all m,n∈N.Thus,we see that ax=(amnxmn)∈CSbpwhenever x=(xmn)∈if and only if z=(zmn)∈Cbpwhenever y=(ymn)∈Lp.This leads us to the fact that B∈(Lp:Cbp).Hence,from Part(iii)of Lemma 2.10 we have

By following the similar way,we have:

We complete the proof.

2.4 Characterization of some classes of matrix mappings

In this subsection,we give the necessary and sufficient conditions on a four dimensional matrix in order to transform the points in the spaceinto the spaces Mu,Cbpand Lq.

Theorem 2.12.Let A=(amnkl)be any four dimensional matrix.Then,A∈(:Mu)if and only if

Proof.Let x=(xmn)∈.Then,there exists a sequence y=(ymn)∈Lpfrom Remark 2.9.Using the relation(1.3)we have for the(i,j)th rectangular partial sum of the series∑k,lamnklxklthat

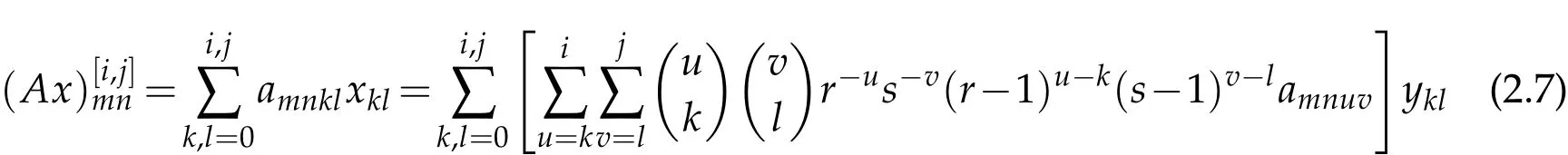
for all m,n,i,j∈N.Define the matrix

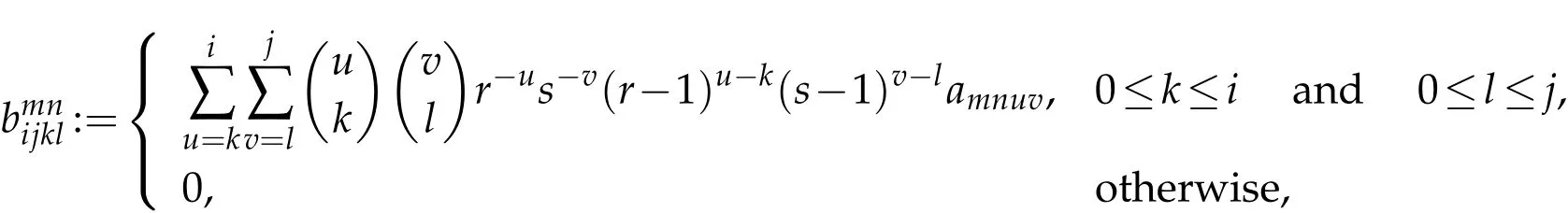
for all i,j,k,l∈N.Therefore,(2.7)can be written asThen,the bpconvergence of the rectangular partial sumsfor all m,n∈N and for all x∈is equivalent to the statement that Bmn∈(Lp:Cbp)and hence the condition

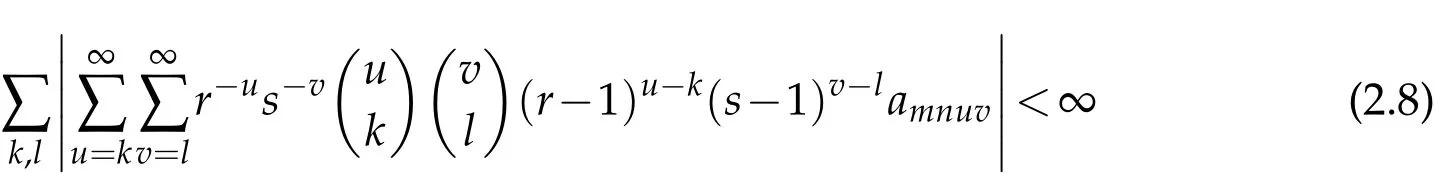
must be satisfied for each fixed m,n∈N.

If we take bp-limit in the terms of the matrix,then we have

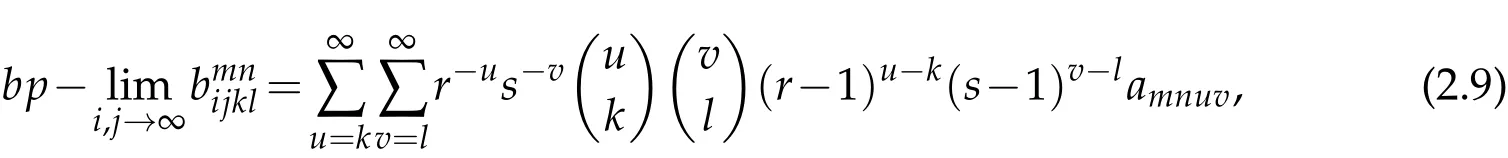
which exists from(2.8).Using the relation(2.9)we can define a four dimensional matrix B=(bmnkl)by

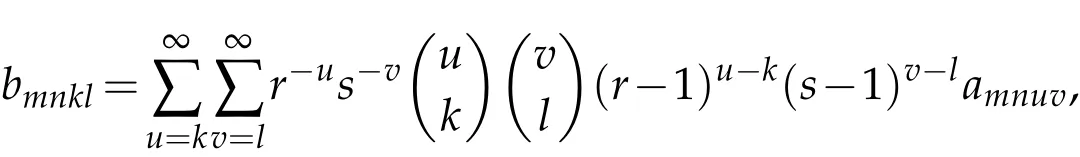
for all m,n,k,l∈N.Therefore,we obtain by the relations(2.7)and(2.9)that

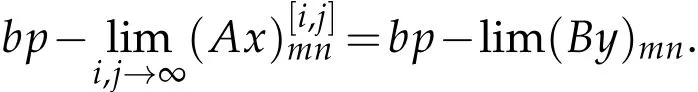
Thus,it is seen by combining the fact”A=(amnkl)∈(:Mu)if and only if B∈(Lp:Mu)”with Part(i)of Lemma 2.10 that

Then,we conclude that A=(amnkl)∈(:Mu)if and only if the conditions(2.8)and(2.10)hold.

Since Theorems 2.13 and 2.14 can be proved in a similar way to that used in the proof of Theorem 2.12,we give them without proof.

Theorem 2.13.Let A=(amnkl)be any four dimensional matrix.Then,A∈(:Cbp)if and only if the conditions(2.8),(2.10)hold and there exists(αkl)∈Ω such that

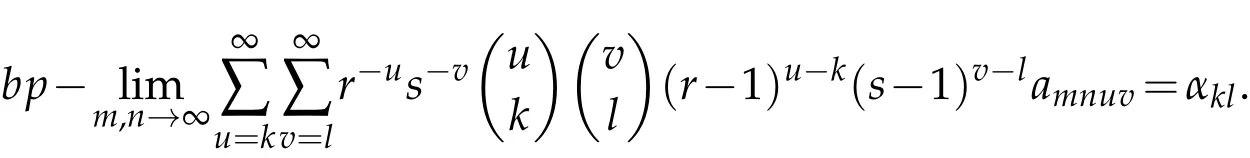
Theorem 2.14.Let 1≤q＜∞.Then,A=(amnkl)∈(:Lq)if and only if the condition(2.8)holds and

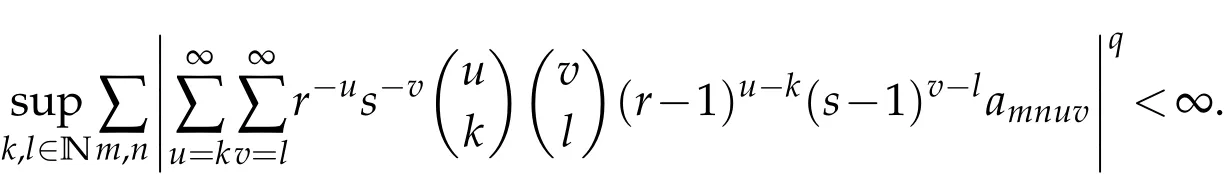
3 Conclusions

By ‘∞,c,c0and ‘p;let us denote the classical spaces of all bounded,convergent,null and p-absolutely summable single sequences,as usual;respectively.Domain of Euler mean Erof order r in the spaces c and c0was studied by Altay and Bas¸ar[3].Later,the domain of Erin the spaces‘∞and ‘pwas investigated by Altay et al.[4]and Mursaleen et al.[14],where1≤p＜∞.Quite recently, as an extension of some of the main results obtained Altayet al. [4] and Mursaleen et al.[14]to the double sequences,Talebi[19]has introduced the domainof four dimensional Euler mean E(r,s)of orders r,s in the spaces Muand Lpof bounded and p-absolutely summable double sequences,where 1≤p＜∞.

In the present paper,as a natural continuation of Talebi[19]we have derived some properties of four dimensional Euler mean E(r,s) of orders r,s and gave the related resultsfor the spacein the case 0＜p＜1. We should note from now on that one can investigate the domain of E(r,s)with algebraic and topological properties in the spaces Cϑand Cϑ0of ϑ-convergent and ϑ-null double sequences for filling out the existing literature,where ϑ∈{p,bp,r}and also can give dual spaces ofwith 1≤p＜∞and some classes of matrix mappings fromwith 1≤p＜∞to certain double sequence spaces.

Acknowledgements

The authors are indebted to the anonymous referee for his/her valuable comments which helped to improve this paper.