一种高纬度区域船舶偏航距离的高精度求解算法

2019-01-08梅斌孙立成史国友马麟李伟峰

上海海事大学学报 2018年4期

梅斌,孙立成,史国友,马麟,李伟峰

(1.大连海事大学 a.航海学院； b.辽宁省航海安全保障重点实验室，辽宁大连 116026； 2.中国船级社，北京 100007)

0 引言

在船舶航行中，由于海洋环境干扰的存在或者避让操作需要，船舶会偏离计划航线一定距离，形成偏航距离(cross track distance)。[1-2]偏航距离在船舶运动控制、靠泊、进出港操纵以及航道规划和航线设计等领域都有应用。在船舶航迹保持控制中，船舶实际位置与计划航线间的偏航距离是航迹保持控制的误差[3]，该误差一般作为控制调节量。对于船舶进出港操纵，船舶与岸线间的偏航距离可用于数字化精确引航。[4]在航道规划和航线设计中，可根据偏航距离，在钻井平台附近、浅水区域设置安全缓冲区域。因此，研究偏航距离的计算方法具有一定的实用意义。

关于偏航距离计算方法，已有许多研究成果。LEE等[5]采用CCD摄像机影像辨别岸基导标颜色，计算船位与导标延伸线之间的偏航距离，实现了视觉导航，用于船舶自动靠泊。基于ECDIS的导航系统一般利用GPS提供的位置信息，计算船舶与岸线之间的偏航距离。[6-7]在汽车自动行驶、飞机航行和水下航行器控制中，需要计算偏航距离[8-12]：汽车的偏航距离定位仪器处于欧氏空间，使用欧氏距离；在飞机航行中，飞行员计算飞机偏航距离时将地球作为球体近似体，精度不高；水下航行器作业范围较小，不需要进行大范围的航线设计，因此水下航行器的偏航距离也是欧氏距离。以上计算方法不能用于船舶偏航距离的计算，这是因为它们采用的大地球体近似体不同。

在船舶航迹保持控制中:FOSSEN[3]采用平面坐标系上的欧氏距离作为控制量，并未论述大地坐标转换，因此不能直接用地理坐标进行航迹偏差度量；张显库等[13]和郑云峰等[14]采用墨卡托投影，将船舶的大地坐标投影到平面直角坐标系内，以欧氏距离作为航迹保持控制的航迹偏差(简称基于墨卡托投影的欧氏距离算法，算法1)；在卫星定位与导航中，使用地心地固坐标系(ECEF)作为惯性坐标系、北-东-地坐标系(NED)作为附体坐标系时，并没有考虑球面上船舶轨迹的弯曲性质[3]。在船舶航行中，船员习惯使用墨卡托投影进行导航，但是墨卡托投影存在长度变形特性，这个特征在高纬度区域更加显著，故当纬度大于86°时不适合使用墨卡托投影。为研究高纬度区域船舶运动的偏航距离计算误差，本文进行偏航距离概念探讨和真值求解算法设计，分析多种算法的误差大小和规律；通过分析地图投影特点，选取适合高纬度区域偏航距离求解的投影算法；在此基础上，根据航海领域的精度需求，推荐偏航距离计算方法。

1 偏航距离计算模型

船舶在地球上航行，偏航距离与地球球体形状和球面线形有关。以下分别对偏航距离的内涵、椭球面算法和后续使用的优化算法进行分析和概述。

1.1 偏航距离内涵

综合IMO、IHO和IALA有关描述，偏航距离是垂直于计划航线(预期航迹)的偏移量，当船舶与该段计划航线的间距超出设置的偏移量时，电子海图系统会发出警报[1-2，7，15]。在航行方法中，大洋航行可选用大圆航线(great circle route)、恒向线航线(rhumb line route)、等纬圈航线(parallel route)和混合航线(composite route)，然后再使用分点将选用的航线分成恒向线。在航用海图上，分航段折线是恒向线航线；大地球体通常采用地球椭球体(Earth ellipsoid)。因此,高精度的偏航距离计算是地球椭球体上船位与恒向线间的距离计算。

如图1所示，航线(恒向线)AiAi+1的延长线与赤道相交于点A0，AiAi+1的航程为S。航行中船舶位于点O2处，与计划航线的偏航距离为O1O2。

图1 偏航距离示意图

1.2 椭球面算法

在偏航距离求解中,采用以下几种椭球面算法进行长度计算和坐标转换。

1.2.1 大地线主题正反解

大地线有3种不同定义，虽然这3种大地线微分方程不同，但是由它们导出的大地线方程相同。本文采用的大地线是连接曲面上两点的最短线。假设已知图1中点O1(φ1,λ1)，则偏航距离O1O2长度即为大地线长度。目前关于地球圆球体和地球椭球体上的大地线主题正反解(direct and inverse solution of geodesic)问题的求解方法很多，文森特公式精度高、适用广，最适合于计算机计算[15]。

1.2.2 恒向线主题正反解

针对恒向线主题正反解(direct and inverse solution of rhumb)问题已有高精度的求解算法。史国友等[16]对恒向线主题正反解问题的求解算法进行了优化。优化后的算法具有不需要迭代和象限判定的优点，在船舶航迹计算和电子海图航线设计中通用性强,适合于计算机计算。本文使用该算法对图1中航段AiAi+1进行恒向线正反解计算。

1.2.3 墨卡托投影正反解

墨卡托投影正反解(direct and inverse solution of Mercator projection)能够实现大地坐标系与墨卡托坐标系间的坐标转换。张显库等[13]和郑云峰等[14]在墨卡托投影坐标上以欧氏距离进行了偏航距离的计算。SNYDER[17]使用等量坐标和级数展开计算了墨卡托投影的正反解，其中等量坐标使用等量纬度正反解实现。本文使用该算法进行墨卡托正反解计算。

1.3 Nelder-Mead simplex算法

Nelder-Mead simplex算法是一种优化算法，它通过迭代求解目标函数的最大值或最小值。这种优化方法不同于COTTLE等[18]提出的单纯形法，被称为下山单纯形法[19]。该算法的低维适用性和不需要求导的特性符合本文后续目标函数的求解要求，因此本文用其进行偏航距离的迭代求解。

2 偏航距离求解的算法设计

在船舶航迹保持控制、靠泊或进出港操纵等应用计划航线进行导航的情境中，需要求解船位与一系列折线的最近距离，这个最近距离就是偏航距离。本文以用计划航线进行导航为例进行算法设计。

2.1 直接求解

直接求解法(以下简称算法2)源于笔者研究团队电子海图模拟器，综合运用了椭球面上大地线主题正反解和墨卡托投影正反解算法，直接计算偏航距离，计算流程见图2。值得注意的是，在船舶定位和航线设计中，点坐标(计划航线转向点和船位点)使用大地坐标系，因此转向点坐标用经纬度表示。

2.2 迭代求解

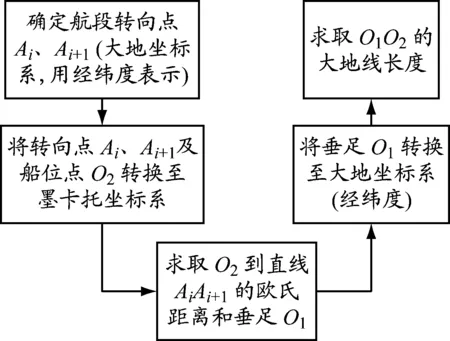
图2 偏航距离直接求解流程

图3 偏航距离迭代求解示意图

如图4所示，迭代求解算法设计思路是：在确定计划航线(预期航迹)航段后，迭代求解船舶与计划航线的最近距离。迭代求解算法采用Nelder-Mead simplex算法。目标函数D连续且一阶微分存在唯一零点，用优化算法取得D的极小值。

图4 偏航距离迭代求解

算法伪代码如下：

输入：船位点O2，计划航线转向点(A1，A2，…，An)

输出：偏航距离

中间变量：航向CAiAi+1、航程SAiAi+1

% 确定计划航线航段，计算航段航向、航程

FOR EACHA∈{A1,A2,…,An-1}

IF球面∠O2AiAi+1<=90°&∠O2Ai+1Ai<90°

[CAiAi+1,SAiAi+1]=InverseRhumb(Ai,Ai+1);

BREAK FOR;

END IF

END FOR

% 航段上任意点与船位的相对距离

相对航段起点Ai真方位C=CAiAi+1

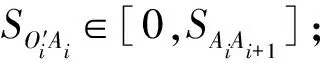
% Nelder-Mead simplex算法

O1= DirectGeodesic(Ai,C,SDmin);%垂足

偏航距离 = InverseGeodesic(O1,O2);

伪代码中:DirectRhumb、InverseRhumb分别为恒向线正、反解计算，DirectGeodesic、InverseGeodesic分别为大地线正、反解计算，Nelder_Mead_simplex为下山单纯形法优化计算。

3 算法误差分析

用算法1、算法2和迭代求解法都能求解偏航距离。用迭代求解法得到的值逼近真值、精度高，将其分别与用算法1和算法2得到的计算结果比较，验证算法1和算法2的精度。

3.1 误差的分析过程设计

如图5所示，为验证算法精度，分别以纬度φ、船舶相对O点的真方位Ψ和恒向线OO2长度作为自变量，设置取值范围分别为0°～90°、0°～360°和1～10 n mile(与NMEA0183中RMB语句中偏航距离范围(0～9.9 n mile)对应)[20]，全局验证椭球体上的偏航距离。

用算法1、算法2和迭代求解法计算船位点O2与航线OAi+1间的偏航距离。将用算法1和算法2求解的值分别减去用迭代求解法得到的值作为误差。如果误差大于0，则用算法1和算法2求解的值大于迭代求解值。

图5 偏航距离计算误差的分析过程设计

3.2 算法1误差分析

将用算法1与迭代求解法计算出的偏航距离的差(即算法1的误差)作为验证指标，检验算法1的可行性和计算精度，结果见图6。

a)OO2=1 n mile时的误差b)真方位为40°时的误差

图6算法1的偏航距离计算误差与恒向线OO2长度、O点纬度和船舶相对O点的真方位的关系

如图6a所示:随着船位相对O点的真方位(0°～360°)的变化，误差几乎不变；随着纬度的增加，误差出现较大变化，这种特征与墨卡托投影特性一致。

如图6b所示：当恒向线OO2长度为1 n mile、纬度为31°时，误差接近0.179 n mile(331 m)；当恒向线OO2长度为5 n mile、纬度为60°时，误差接近5 n mile。在船舶避碰或大洋航行的应用中，误差的影响较为明显。出现误差的原因是，墨卡托投影保证了等角和航海视觉习惯[21]，但无法保证等积、等距离。

3.3 算法2误差分析

墨卡托投影导致子午线(弧长)发生形变[16]，算法1误差较大。算法2中使用了墨卡托投影，因此有必要验证算法2在全局纬度上的计算精度。将用算法2与用迭代求解法计算出的偏航距离的差(即算法2的误差)作为验证指标，检验算法2的可行性和计算精度，结果见图7。

a)OO2=1 n mile时的误差b)O点纬度为89°时误差与真方位的关系

c)真方位为0～360°时误差最大值与纬度的关系d)O点纬度为89°时直接与迭代求解的垂足间距离与真方位的关系

图7算法2的偏航距离计算误差与恒向线OO2长度、O点纬度和船舶相对O点的真方位的关系

图7展示了算法2的偏航距离计算精度。由图7a可知，O点纬度在0～80°范围内时误差较小，在80～90°范围内时误差较大；船舶相对O点的真方位在0～360°范围内时误差呈现双峰形状。由图7a～7d可知，OO2=4，7，10 n mile时的误差大于OO2=1 n mile时的误差。

图7b解释了船舶相对O点的真方位对误差的影响。误差最大值出现在船舶相对O点的真方位为90°或270°左右时，即船舶航向为0°或180°时，与迭代求解值呈非线性增函数关系。

图7c展示了高纬度区域算法2误差的数量级与纬度的关系。当O点纬度在89.6°～89.7°范围内且OO2=10 n mile时，误差为400～900 m；在高纬度区域，误差非线性增长。

图7d展示了当O点纬度为89°时，用算法2和迭代求解法求出的垂足不在同一位置，即算法2求解的空间物标跟踪定向航行船舶的最近距离点精度不准。

综上可知：低纬度区域(0～80°)算法2计算精度较高；当船舶在高纬度(80°～90°)区域航行时，算法2近距离计算精度较高，远距离计算误差较大。

4 改进的直接求解算法及其误差分析

由于墨卡托投影的性质，高纬度(80°～90°)区域算法2的误差较大。现有投影变换都不能兼顾等角、等积和等距离条件，各种投影具有各自的特点，在极端情况下都会出现投影变形。

针对高纬度区域，SKOPELITI等[21]推荐电子海图系统使用的等距方位投影和正轴正射投影，以保持形状不变。此外随着极地规则[22]的生效和IHO下属ACHR(Arctic Regional Hydrographic Commission)对极地区域的持续关注[23]，高纬度区域航行越来越受到重视。

本文选择极点为投影中心的等距方位投影作为直接求解的投影变换，即图2第2步使用正轴等距方位投影(azimuthal polar equidistant projection)直接求解(以下简称算法3)。这种投影的特点是：极点处无变形；距离极点越远，面积变形越大，角度变形越大。[21]将算法3用于图5偏航距离计算误差的分析过程设计中，并进行与用迭代求解法得出的结果之差(即算法3的误差)的计算。如图8所示：当纬度在80°～90°范围内，恒向线OO2长度分别为1、4、7、10 n mile时，对应误差均值分别为0.000 9、0.003 3、0.002 7、0.011 8 m，误差很小；在O点纬度为0°时误差达到最大；误差峰均有4个。算法3有效提高了高纬度区域偏航距离的求解精度。

a)OO2=1 n mile时误差b)OO2=4 n mile时误差

c)OO2=7 n mile时误差d)OO2=10 n mile时误差

图8算法3偏航距离的计算误差与纬度和真方位的关系

5 实例

5.1 中纬度区域

在水上水下通航安全的工程中，存在计算钻井平台与航道距离的案例。为评估钻井平台对航行的影响，需要计算钻井平台与航道(延长线)的距离。如图9a所示，钻井平台处于黄骅港进出港航道边缘。计算垂足O1和偏航距离并与电子海图测量值比对，见图9b。

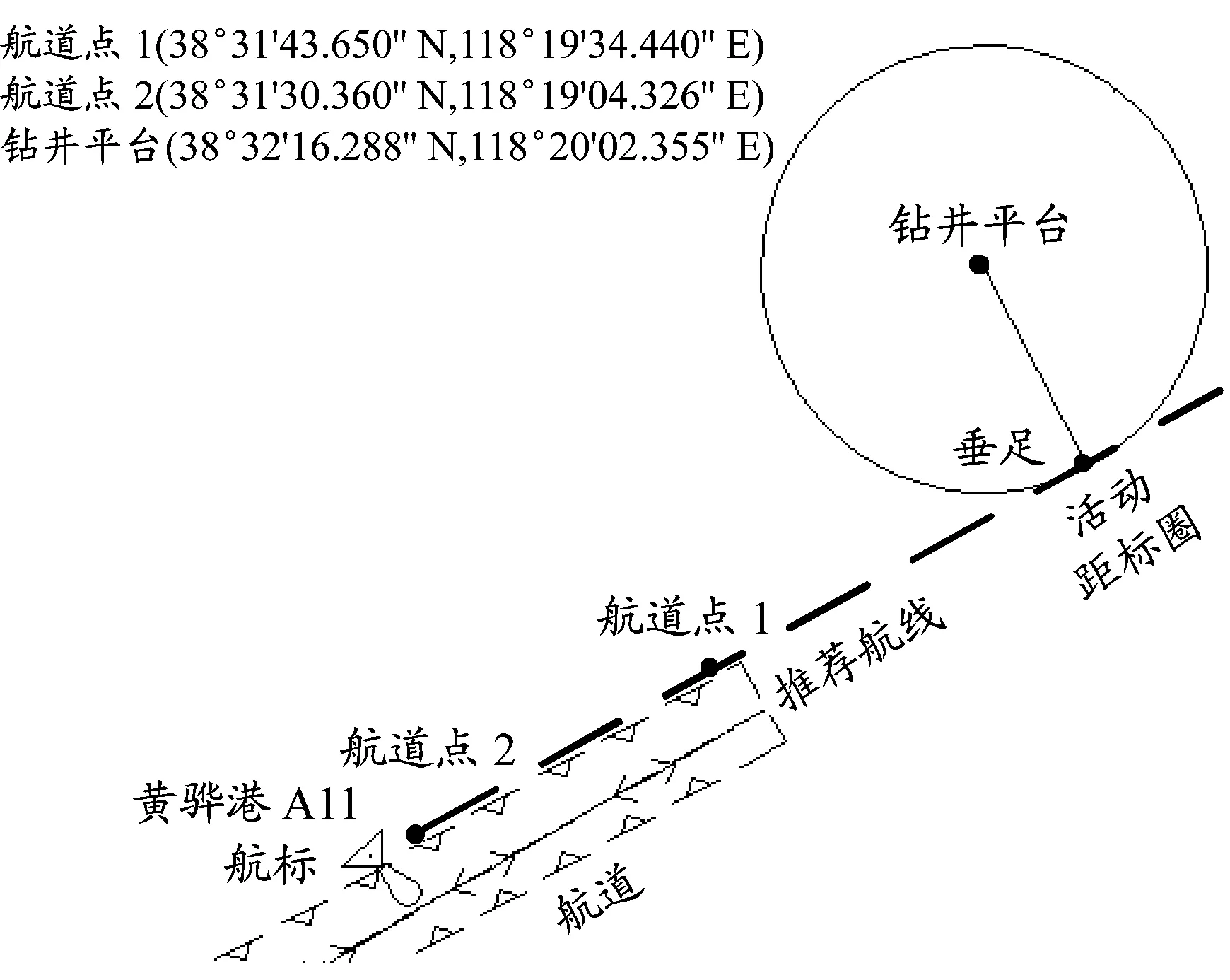
a)钻井平台与航道的位置关系

b)迭代次数与偏航距离的关系

电子海图活动距标圈、算法2、迭代求解法和算法1得出的偏航距离见表1。由于电子海图活动距标圈是手动测量的，所以误差较大。算法2与迭代求解法得出的结果相近。算法1的偏航距离的计算误差较大。算法1是用墨卡托坐标计算的，计算的垂足用墨卡托坐标表示，因此没有垂足的经纬度。

表1 中纬度区域钻井平台与航道(延长线)间偏航距离计算结果比对

5.2 高纬度区域

假设高纬度区域存在转向点A1(89°36′N，0°E)、转向点A2(89°42′N，0°E)、船位点O2(89°36′N，24°30′E)。与中纬度区域实例类似，高纬度区域船位点O2与恒向线A1A2间的偏航距离计算结果见表2。由于电子海图活动距标圈是手动测量的，所以误差较大。算法3与迭代求解法得出的结果相近，并且二者与算法2得出的结果相差约432 m。与中纬度区域应用一样，算法1的偏航距离计算误差较大，并且是墨卡托坐标上的值，因此没有垂足O1的经纬度。