基于最小二乘支持向量机的AIS数据修复方法
2019-01-08王永明刘兴龙桑凌志
王永明,刘兴龙,桑凌志
(1.大连海事大学航海学院,辽宁 大连 116026;2.闽江学院物理与电子信息工程学院,福州 350108;3.中国交通通信信息中心交通安全应急信息技术国家工程实验室,北京 100011)
0 引 言
我国是世界主要航运大国,航运的安全有序对国家具有重要的战略意义。水上交通安全是航运发展永恒的主题,加强水上交通管理的信息化、智能化是维护水上交通安全的重要方式。在水上智能交通运输体系中,船舶时空轨迹信息的感知和处理是整个体系的核心。传统船舶轨迹数据的获取方式非常有限,主要是依靠航海日志、船舶进出港报告和海事雷达回波信号等,而且获取成本高、样本少、时间跨度短,难以长时间地观测和记录大量船舶在海上的行驶过程。
自2002年《国际海上人命安全公约》(SOLAS公约)强制推行船舶自动识别系统(automatic identification system,AIS)以来,AIS受到了全球航运界的广泛关注。AIS通过甚高频(VHF)将船舶静态信息和动态信息广播至附近水域的他船和岸基,使船舶之间可进行相互协调,同时使海事部门能够对船舶进行监控和管理,提高了船舶通行能力和安全保障能力。[1]AIS数据在航道通过能力评估、船舶交通流分析[2-3]、水上交通安全评价[4-6]等方面具有广泛的应用。
船舶静态信息指船舶MMSI号、船名、船舶类型、船宽、船长等信息,在一般情况下不允许修改。船舶动态信息指船舶航行位置(一般用船舶的经纬度坐标表示)、航速、航向(包括对地航向、真航向)等,这类数据大多由设备获取,受人的因素影响较小。当AIS设备未与罗经连接或舶舶位置数据转换信号出现较大误差时,发送的AIS动态数据会出错。动态数据的发送也可能受到干扰,导致数据异常。BALDAUF等[7]对实地AIS数据发送时间间隔和动态数据可靠性进行了调查研究,发现大量AIS数据不符合技术规范。常会振等[8-9]等通过统计分析发现,大量AIS数据不符合IMO规范。
基于上述原因,对AIS数据进行可靠性评估和错误数据识别方法研究具有重要意义。国内外已经开展了一些研究:吴建华等[10]对错误致因进行分类并据此对异常轨迹进行分类,分别提出了各类异常数据自动检测依据。ZHANG等[11]、刘磊等[12]和SANG等[13]通过构建AIS异常数据识别规则、设置数据阈值,将异常轨迹点或异常航速等数据删除。卫桂荣等[14]提出了MMSI校验码、填充位和校验码的综合检测,静态信息与动态信息匹配校验,以及异常点数据检测等数据检测方法,以减少AIS数据库中的异常数据。总之,AIS错误数据识别主要依靠的仍是设置阈值,缺乏有效的评估并修复数据的模型。
以往主要使用数据插值方法对AIS轨迹数据进行修复:吴建华等[10]和田利芹等[15]均采用三次样条插值修复数据,取得了一定的效果;刘磊等[12]采用分段三次Hermite插值修复数据;鉴于AIS数据标准时间间隔的差异性,NGUYEN等[16]首先对时间序列进行特征识别,继而采用分段线性插值或分段三次Hermite插值修复数据,该方法对一类AIS数据具有自适应修复能力;SANG等[17]分别采用分段线性插值、分段三次样条插值和分段三次插值对船舶轨迹进行了还原,发现分段三次样条插值的轨迹还原精度最高。
AIS作为重要的水上交通信息感知工具,在海事监管和船舶避碰方面有着极其重要的作用。然而,当前的AIS数据由于存在大量错误和缺失,尚不满足船舶避碰决策和海事监管的要求。在基于AIS数据的船舶时空轨迹修复方面,目前基于插值的AIS数据修复方法只考虑AIS数据中的船舶位置信息,故需要引入AIS数据中的航速和航向信息以提高轨迹还原的精度,同时修复AIS数据中的航速和航向信息。
本文首先解决AIS动态数据发送周期的不同步问题,通过时间匹配解决模型的时间参数输入问题,然后利用AIS历史数据库中的相似轨迹建立船舶轨迹回归模型,最后基于最小二乘支持向量机(least squares support vector machine,LSSVM)对船舶位置、航速、航向等分别进行训练,通过案例实现对AIS动态数据的有效修复。本方法可以有效帮助航程较远船舶AIS轨迹数据的还原,进而帮助水上交通主管部门准确获取船舶航行轨迹、船舶行为、避碰决策等相关信息,推进现有各类信息化系统的使用,为海事大数据的应用、智慧海事的发展提供良好的AIS数据基础。
1 基础理论与方法
1.1 时空轨迹相似度
船舶时空轨迹相似度反映的是两艘船空间运动趋势的一致性和轨迹曲线的贴近程度。评估船舶时空轨迹的相似度并不是根据一定准则给两条轨迹的相似程度“评分”,而是对一条指定的船舶轨迹,从历史船舶轨迹数据库中找出一条与其趋势最一致的轨迹曲线。对于一条指定的轨迹Trj,给出一个包含若干条轨迹的轨迹数据库T,从T中返回一条轨迹T′∈T,使得
d(T′,Trj)≤d(X,Trj), ∀X∈T
(1)
式中,d(·)为两条轨迹间的距离度量函数。
可见,在查询相似轨迹时,度量轨迹相似度的核心是距离度量函数。AIS数据发送周期随船舶运动状态而变化,导致不同船舶的轨迹点数且不同,因此船舶运动轨迹相似度的衡量,是不同轨迹点数目下轨迹间的距离度量。两条轨迹之间的距离通常由轨迹点之间距离的聚合来度量。Hausdorff距离是常用的能够处理轨迹点数目不等情形下轨迹间距离度量的方法,具有计算复杂度相对较小的优点。
Hausdorff距离主要描述的是两组轨迹点之间的相似度,它是采用一条轨迹中每个轨迹点与另一条轨迹中轨迹点距离最小值中的最大值来表示的。设两条船的轨迹分别用轨迹点集合A(a∈A)和集合B(b∈B)表示,则两条轨迹的Hausdorff距离计算式为
H(A,B)=max(h(A,B),h(B,A))
(2)
式(2)是两条轨迹间的双向Hausdorff距离,其中:
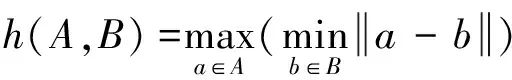
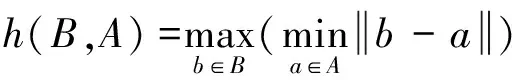
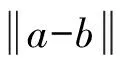
从式(2)可以看出,两条轨迹间的双向Hausdorff距离H(A,B)是两条轨迹间的单向Hausdorff距离h(A,B)和h(B,A)中的较大值,它描述两条轨迹之间的最大不匹配度。
1.2 LSSVM
支持向量机(support vector machine,SVM)是20世纪90年代中期被提出来的一种分类学习机,其内涵是根据小样本数据建立一种非线性的高维映射,从而回归出一个超平面,进而实现数据的分类。LSSVM是SUYKENS等[18]提出的一种改进的SVM模型,它将传统SVM中的不等式约束改为等式约束,采用最小二乘线性系统作为损失函数,代替传统的SVM采用的二次规划方法,将其转化为求解线性方程组的问题。LSSVM方法提高了求解速度和收敛精度。
在修复船舶轨迹时,可以把经度、纬度、速度和航向均当作一维时间序列。假设有N条相似轨迹样本集合{xk,yk,vk,αk}作为训练样本集,其中k=1,2,…,N,x、y、v、α分别代表轨迹数据中的经度、纬度、速度、航向。每个轨迹样本包含4个一维向量,对应输出4个预测值。根据统计学理论,船舶轨迹回归预测优化问题可描述为
(3)
式中:φ(·)为核空间映射函数;ω∈RN为权矢量;ek∈R为误差变量;e=(e1,e2,…,eN)T;c为偏差量;γ为正则化参数。核函数φ(·)可以将船舶轨迹数据原始序列样本映射成为高维特征空间中的一个向量,从而解决线性不可分的问题。一般用拉格朗日法求解这个优化问题:
Γ(ω,c,e,α)=JP(ω,e)-
(4)
其中:αk为拉格朗日乘子,αk∈R,k=1,2,…,N;α=(α1,α2,…,αN)T。根据KKT条件可得到
(5)
这将优化问题转变为线性求解问题,即
(6)
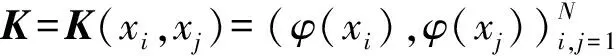
(7)
2 AIS动态数据可靠性评估
2.1 数据丢失时间匹配
AIS动态信息的发送周期与船舶的航行动态相关。高航速和转向都会导致AIS动态信息发送时间间隔缩短。根据实际航行情况,一般船舶的AIS船台动态信息报文发送周期主要为10 s和30 s[19]。然而,现实中存在很多不符合规范的AIS船台,如存在大量周期为15 s的AIS船台。因此,需要对周期不符合规范的AIS船台数据进行处理,使它们与常见周期匹配。本次匹配周期选择为3 s,数据明显超出此周期才能判定为数据丢失。具体的丢失时间匹配流程见图1。
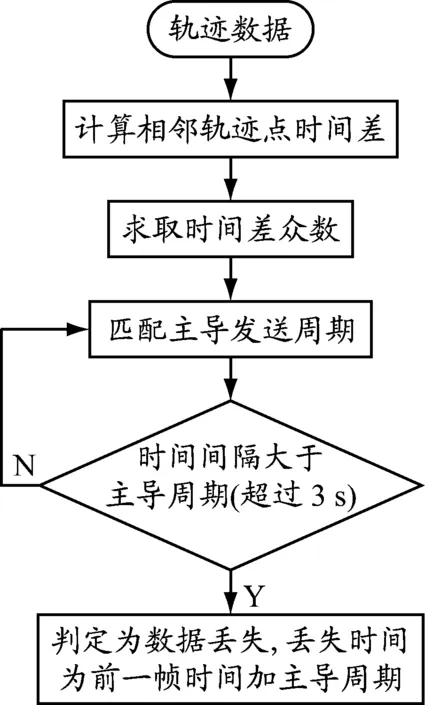
图1AIS数据丢失时间匹配流程
2.2 完备AIS轨迹库制定
采用分段三次Hermite插值可以对3个连续轨迹点以内的AIS数据进行高精度修复,因此首先需要对短距离(3个连续轨迹点以内)的AIS数据进行修复,得到完备的AIS轨迹数据库,再对长距离的AIS动态数据,采用相似轨迹回归预测的方法进行修复。
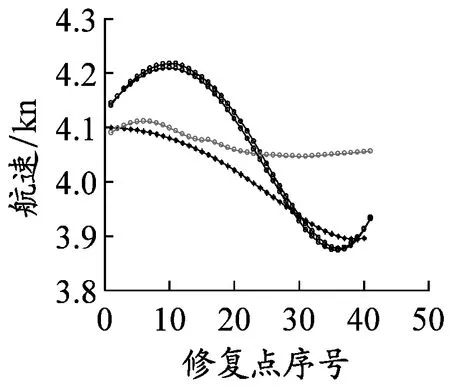
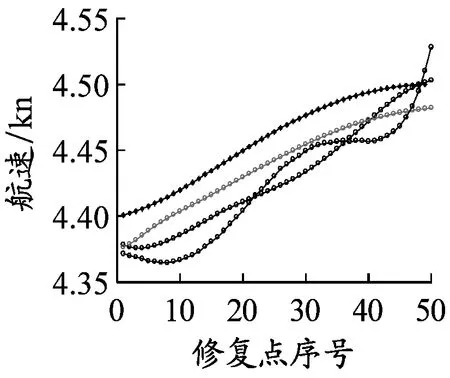
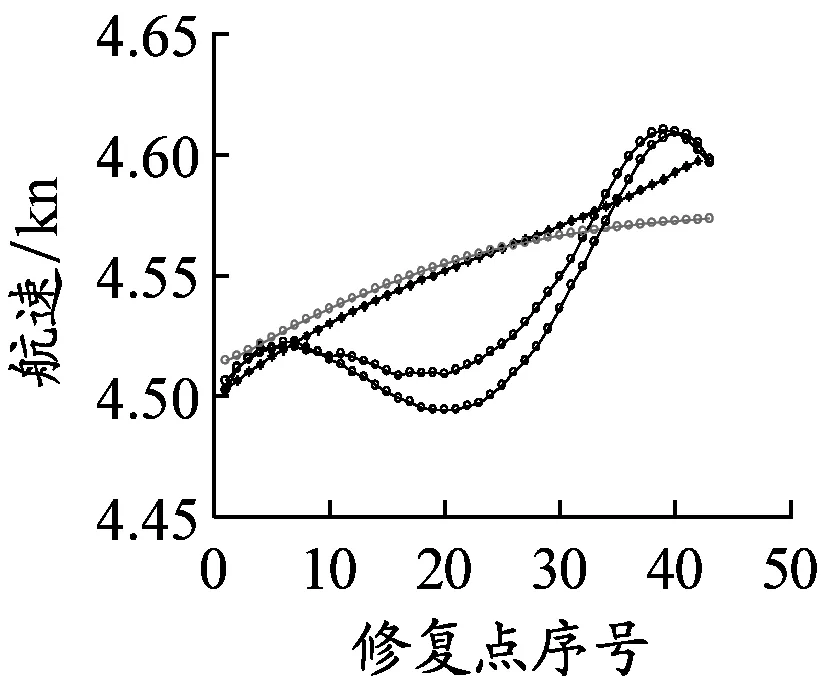
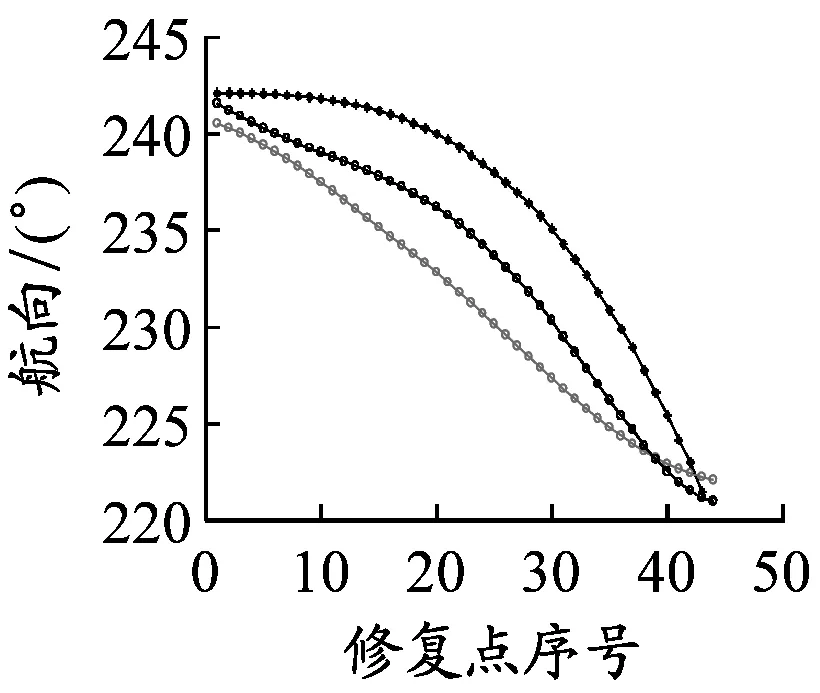
以长江武汉段为例,原始AIS数据经过数据清洗和甄别之后,会出现大量的轨迹点空缺。当前后两条数据的时间差大于90 s时,该条船舶轨迹会被截断,形成两条单独的轨迹。如果所有的船舶轨迹连续丢失点数量均少于3个点,则可以采用分段三次Hermite插值予以修复,形成完备的AIS轨迹历史数据库。选取2015年6月2日中午11:04至11:15某船(MMSI为413940407)的AIS动态数据,采用分段三次Hermite插值对该船的经度、纬度、航速和航向的修复结果见图2。由图2可见,采用分段三次Hermite插值能够有效修复短距离的AIS数据,形成完备的AIS轨迹数据库。
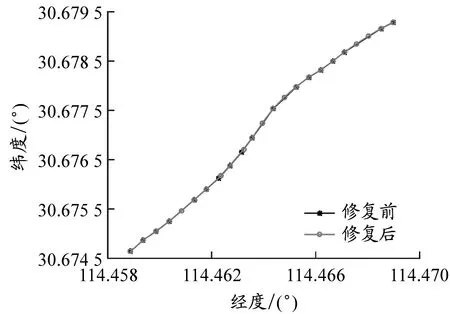
a)经度和纬度
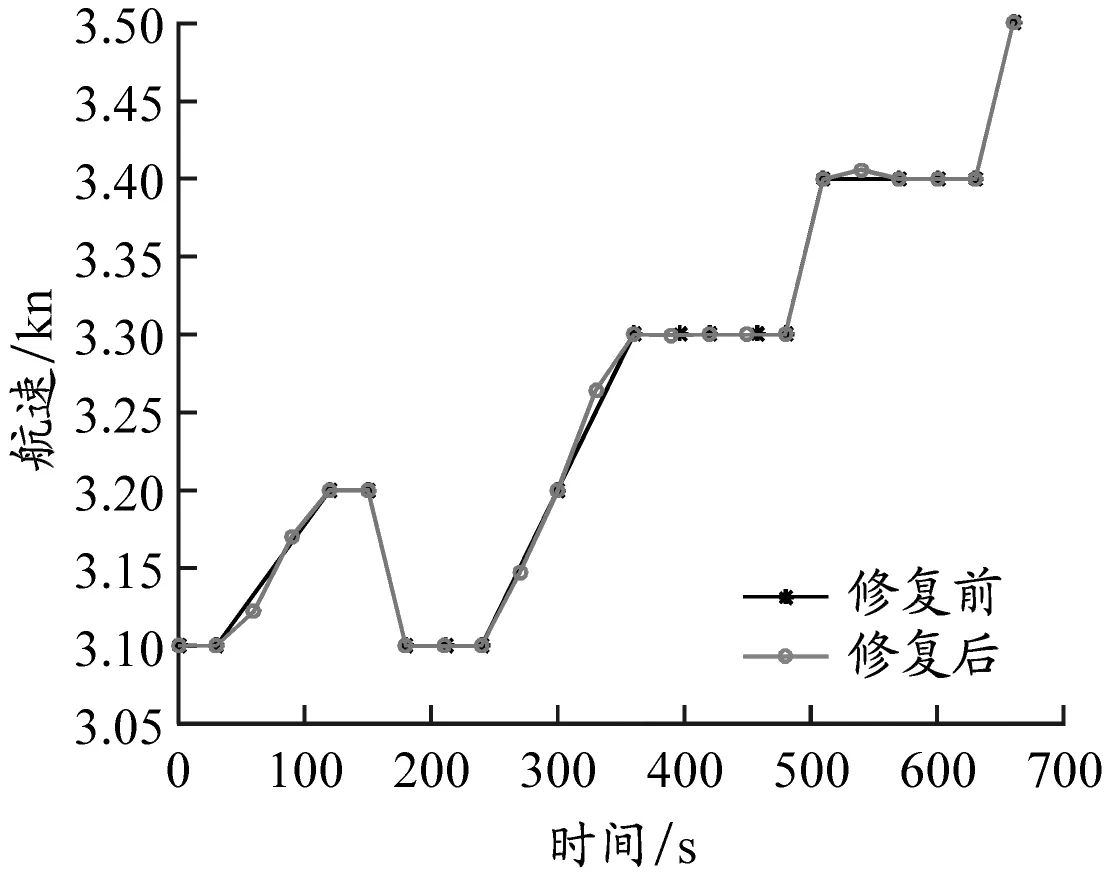
b)航速

c)航向
2.3 相似AIS数据查询与检索
船舶轨迹数据具有时空和大数据特征(即数据体量巨大),且轨迹点序列在时空上并非严格匹配对齐。为解决搜索大数据样本效率低的问题,本文提出一种两层匹配方法。若使用该方法时出现无法匹配的情况,则需要进一步扩大AIS数据搜索的时间范围。
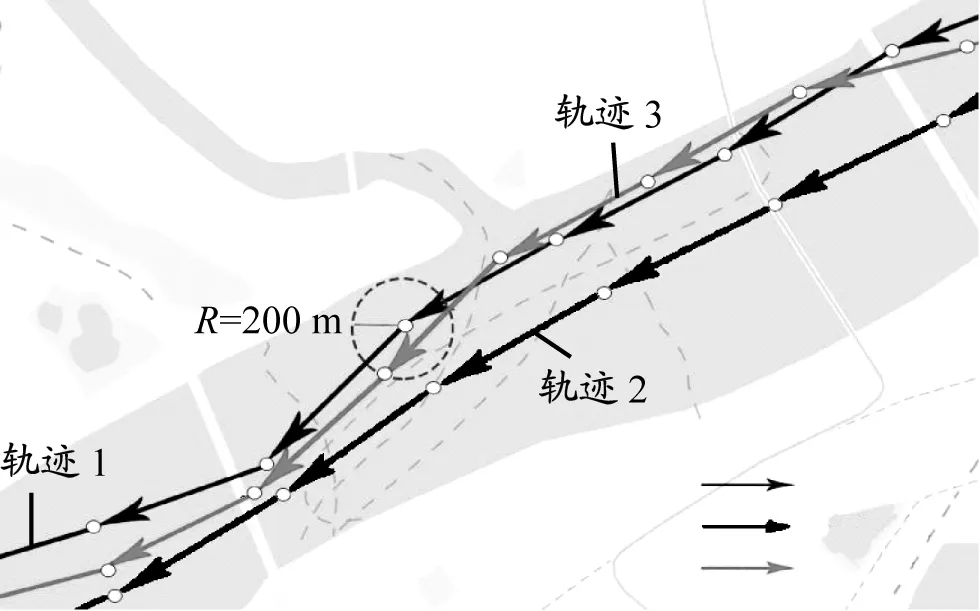
图3 轨迹粗匹配示意图
(1)粗匹配。以序列初始坐标值起始点(X,Y)为中心,200 m为半径,由近至远搜索轨迹点,若搜索到的点处于待匹配轨迹集内,则将该点纳入备选点,同时将该点轨迹纳入粗匹配轨迹集。考虑到内河船舶航速通常不超过10 kn,在AIS数据发送周期(30 s)内船舶运动距离不超过155 m,以及GPS的漂移等因素,以200 m作为半径可以保证相近轨迹点被选中。图3中,轨迹1为样本轨迹,以200 m为搜索半径,轨迹3中存在一个点处于搜索范围内,因此将轨迹3选中。为提高算法效率,设定粗匹配搜索结束的两个终止条件为:①备选点达到50个;② 200 m内没有其他待匹配点。
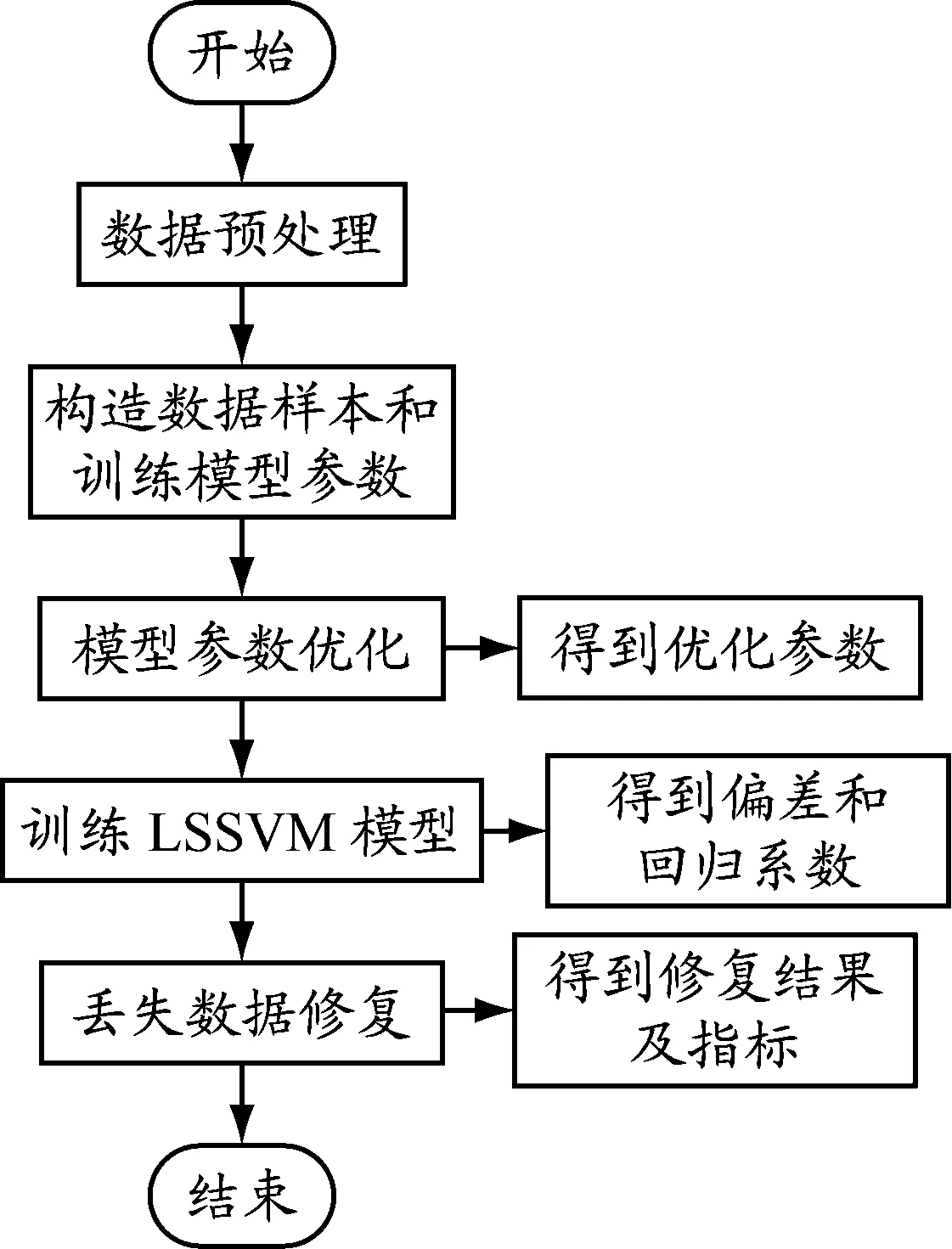
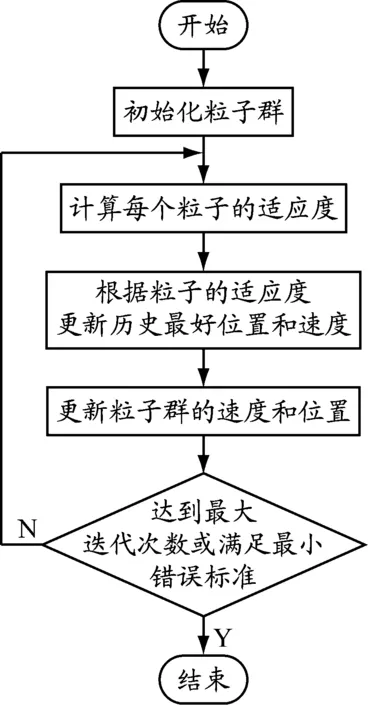
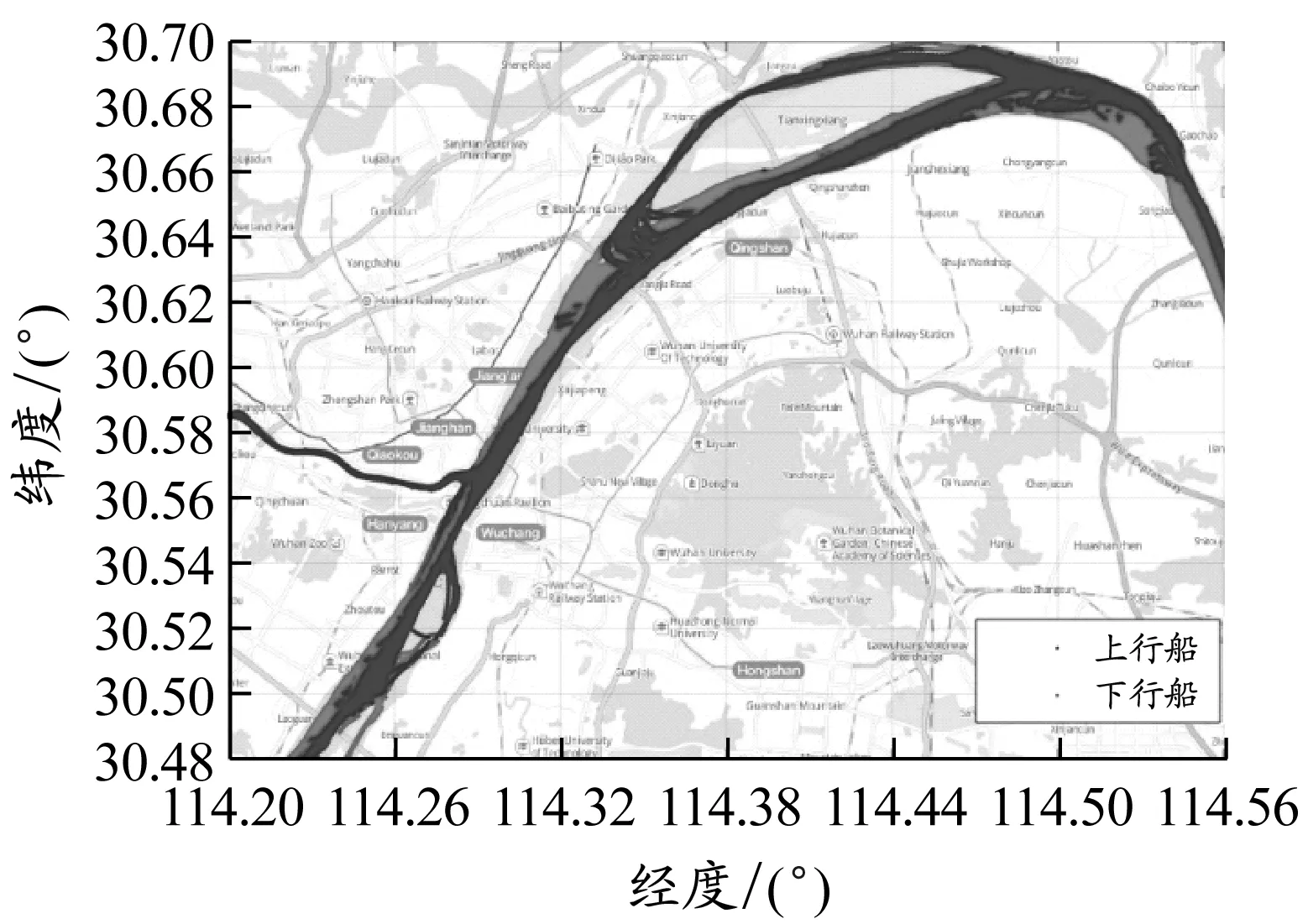
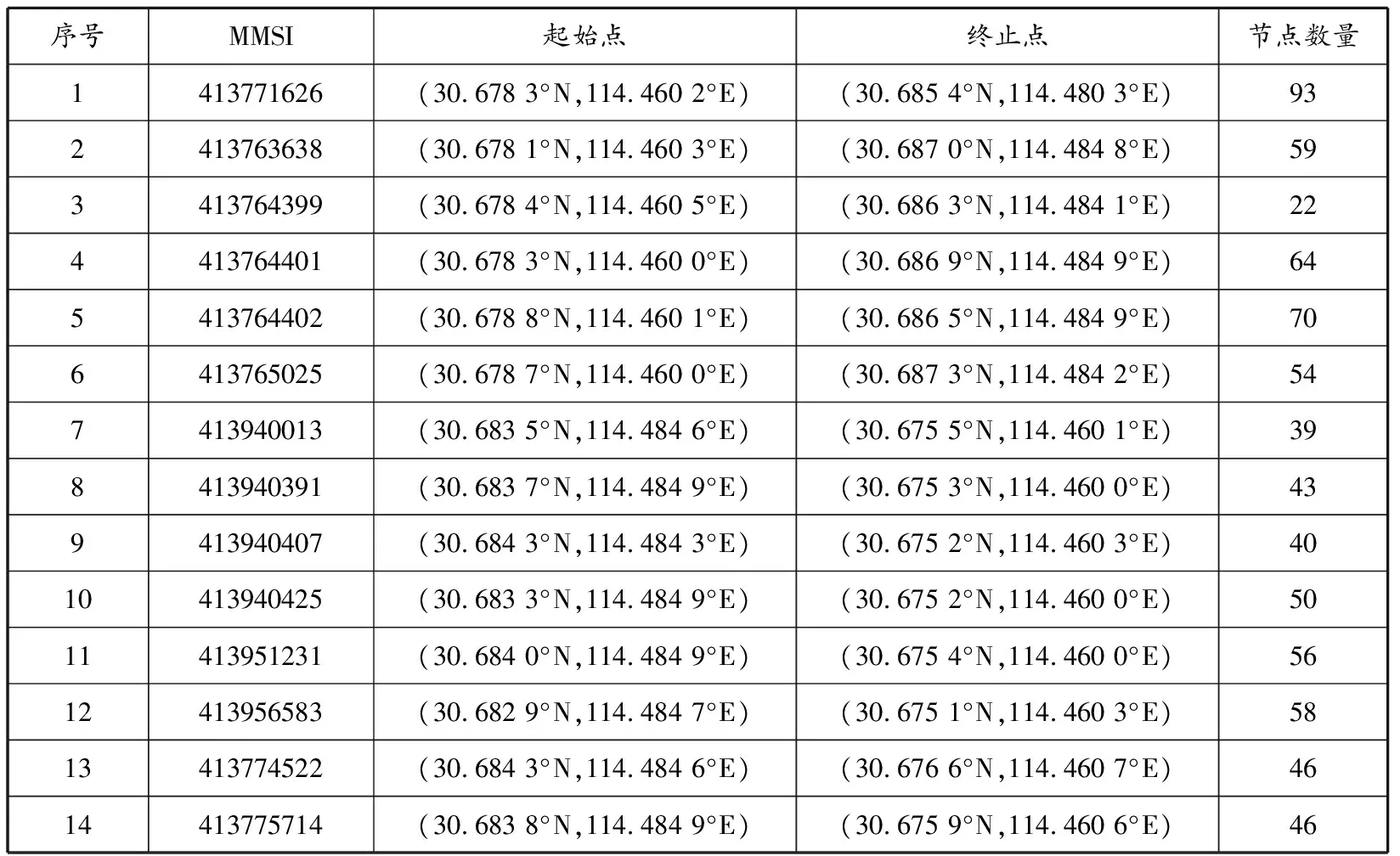
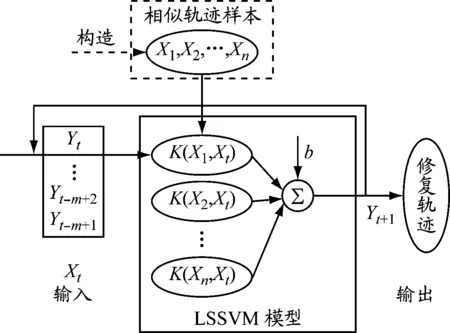
(2)细匹配。在粗匹配轨迹集Tx={T1,T2,…,Tn}中,对每条轨迹Ti进行跟踪搜索,直到该条轨迹中存在点满足如下条件:O(Ni,Ne) 船舶航速的不同,在一个AIS动态报文发送周期内,船舶的航程也不同,导致轨迹点集的疏密程度不同,使得待匹配序列点与模板点无法实现精确对齐。针对不匹配的两个AIS序列集,本文采用Hausdorff距离作为其相似度度量空间。设两条轨迹相似度可表示为S(p,q),其定义为 S(p,q)=H(p,q)+|Np-Nq| (8) 式中:Np和Nq分别表示轨迹p和q的节点数量。 船舶轨迹信息中,最能表征船舶运动信息的特征即为航向特征和航速特征。基于Hausdorff距离的相似度可以表征船舶在航向特征上的相似度。 船舶在航道中的行为通常隐藏着固定的模式,这种行为模式实际上是历史AIS数据和当前AIS数据都具有的一种函数关系。基于LSSVM的AIS数据修复步骤见图4。LSSVM中核函数是关键要素。核函数有很多种,径向基函数(radial basis function,RBF)是最为常用的,对不同大小的样本和不同的维度都具有很好的适应性。本文选定RBF作为模型的核函数。 图4基于LSSVM的AIS数据修复步骤 图5 PSO算法流程 基于RBF的LSSVM回归模型的两个超参数(惩罚系数和核函数宽度)决定船舶轨迹数据回归中LSSVM的泛化能力。随着智能优化算法的发展,粒子群算法、蚁群算法、遗传算法等被用于求取LSSVM模型参数,其中粒子群算法以其编程简单、搜寻速度快的优点,成为应用最广的参数确定算法。本文采用粒子群优化(particle swarm optimization,PSO)算法得到LSSVM回归模型的两个超参数值。 基本粒子群算法的应用具体包括算法流程、算法的参数设置和算法的终止条件。PSO算法流程见图5。 为验证本文提出方法的有效性,在长江中游的武汉段开展验证试验。从宝船网取得2015年6月1日至8月31日3 001万余个原始AIS数据。地域范围为东经114.21°至114.56°,北纬30.48°至30.70°,河段长度大约为30 km。 将获取的原始AIS数据列表后,制定分段规则:(1)对MMSI进行排序,如果前后MMSI不一样,则确定前后轨迹为不同船舶的轨迹。(2)对于每艘船的AIS轨迹数据,根据时间顺序排序,获取AIS时序数列。对于AIS船台,信息发送周期以30 s居多,如果前后轨迹的时间间隔大于90 s,则确定前后轨迹为不同船舶的轨迹。 首先对AIS数据根据MMSI进行排序操作,共分离得到8 520条船舶轨迹,其中上水船轨迹4 000条,下水船轨迹4 520条。根据UTC时间对轨迹数据排序,当前后数据的时间差大于90 s时,则认为出现长距离的数据丢失,确定前后轨迹为不同船的轨迹。分离后的时间间隔小于90 s的子轨迹共有18 520条。经过清洗后的轨迹数据见图6,浅色点为下行船的轨迹,深色点为上行船的轨迹。 图6 长江武汉段水域船舶轨迹库 清除错误的AIS数据后,需要重新计算时间差,将时间间隔大于90 s的轨迹分离为两条单独的子轨迹。针对少量缺失的AIS轨迹,采用分段三次Hermite插值进行初始修复,获取完备AIS轨迹库。 在已建立好的AIS轨迹数据库中,选取一条轨迹数据进行相似轨迹样本搜寻。选择长江武汉段天兴洲下游航道中间部分为起始点,一条下行船轨迹为目标轨迹,进行轨迹库快速检索。共得到14条待匹配轨迹,见表1。在检索结果集中,使用第2.4节的方法进行计算,结果见表2。根据计算结果,第8条轨迹为匹配结果。 图7为AIS动态数据修复流程。在预报过程中,每修复一个点的数据,就将该数据加入LSSVM模型输入中,并去除最后一个旧数据点,以构成新的模型输入,进行循环预报,直至完成全部AIS数据的修复工作。n为所构造的相似轨迹样本的长度,m为自相关时间序列长度,Yt为t时刻所预报的值。因此,AIS动态数据修复分为相似样本训练、数据修复两个步骤。 表1 快速检索结果 表2 轨迹相似度匹配结果 图7 相似样本训练和数据修复流程 4.3.1 样本训练 长距离AIS数据的修复准确程度由两方面的因素决定:一方面是相似样本与待修复轨迹的相似程度;另一方面是LSSVM方法对相似样本的建模精度。使用PSO算法优化后的LSSVM方法对相似样本进行建模(记为PSO-LSSVM模型),当拟合精度达到要求后,进行缺失数据的预报。由于AIS数据样本量较大,采用实时性好的全局PSO算法进行优化。试验对比分为两组:一组是优化前后的LSSVM方法对相似样本建模精度的对比;另一组是优化后LSSVM方法与插值法对丢失数据修复的对比。共有4条轨迹及其相似轨迹被选中作为验证。 根据训练模型预报的拟合程度来评价LSSVM方法对相似样本的建模精度,选取均方根误差作为拟合程度的目标函数。 由上述相似样本所训练的模型(PSO-LSSVM模型)可以直接进行待修复轨迹的预报,经度、纬度、航速、航向的修复模型参数见表3。 4.3.2 数据修复 训练完PSO-LSSVM模型参数后,即可进行该航段长距离AIS数据的修复。由于实际修复时待修复样本数据不可知,使用一组相似样本中的一条轨迹数据作为训练数据,另一条作为假设待修复数据。分别利用分段三次Hermite插值、LSSVM、PSO-LSSVM方法对数据进行修复,结果对比见表3,修复效果见图8。从表3可以得出,对于选定的4组数据样本,在船舶AIS数据的经度、纬度、航速、航向数据修复中,采用PSO算法优化后的LSSVM修复误差要远小于未优化的LSSVM和传统的分段三次Hermite插值的修复误差。 表3 PSO-LSSVM模型参数及3种方法的修复误差对比 a)第1组的经度、纬度 b)第2组的经度、纬度 c)第3组的经度、纬度 d)第4组的经度、纬度 e)第1组的航速 f)第2组的航速 g)第3组的航速 h)第4组的航速 i)第1组的航向 j)第2组的航向 k)第3组的航向 l)第4组的航向 图84组数据的修复结果 (1)AIS在海事监管和船舶避碰方面有着极其重要的作用。由于AIS数据存在大量错误和缺失,当前AIS数据质量尚不能满足船舶避碰决策和海事监管的要求。 (2)通过匹配AIS数据丢失时间,制定完备AIS数据库;采用改进的Hausdorff距离计算公式,融合了轨迹空间相似度和船舶航行速度相似度,为AIS数据修复提供数据基础。 (3)选取长江武汉段进行验证。采用相似轨迹作为LSSVM方法的输入样本,通过数据训练得到回归模型,结果显示本文提出的PSO-LSSVM方法与其他方法相比,能够准确地还原AIS数据。 (4)研究结果有助于改善AIS数据连续性差、完整性不足的问题,通过提高AIS数据质量,进一步实现对船舶运动规律等的有效分析,推进现有各类信息化系统的使用,为海事大数据的应用、智慧海事的发展提供良好的AIS数据基础。2.4 AIS数据相似度评判
3 基于LSSVM的AIS数据修复
4 案例验证
4.1 历史轨迹库制定
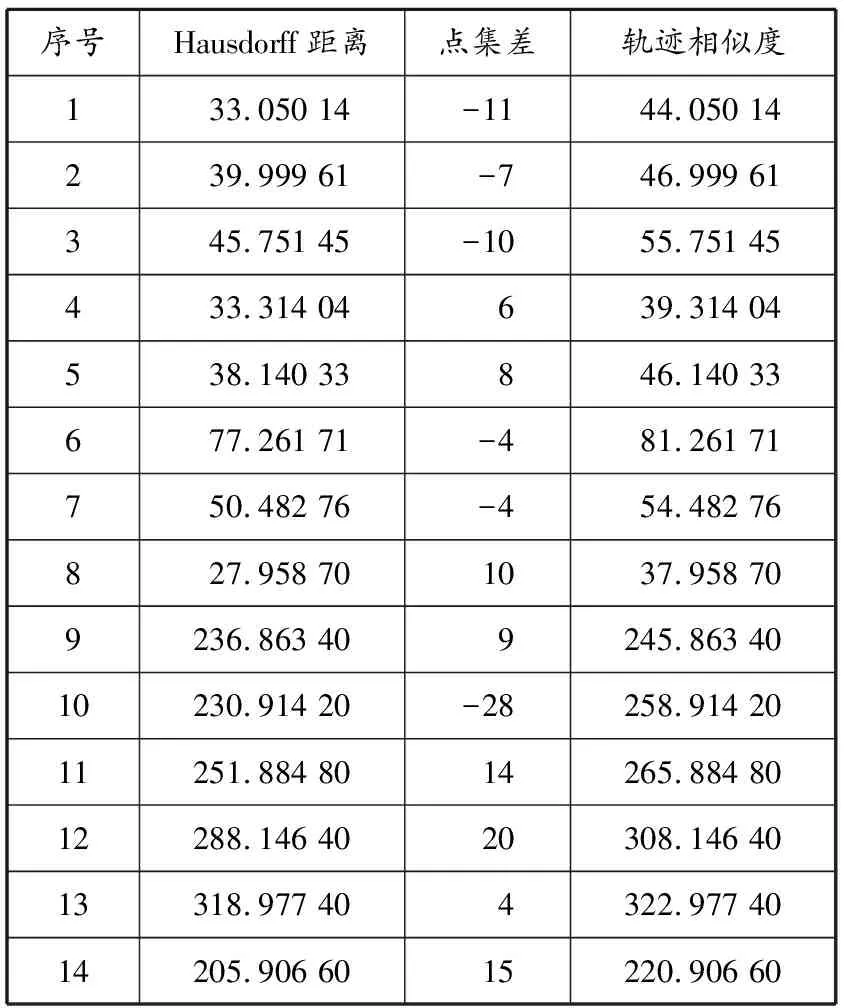
4.2 相似轨迹样本搜寻
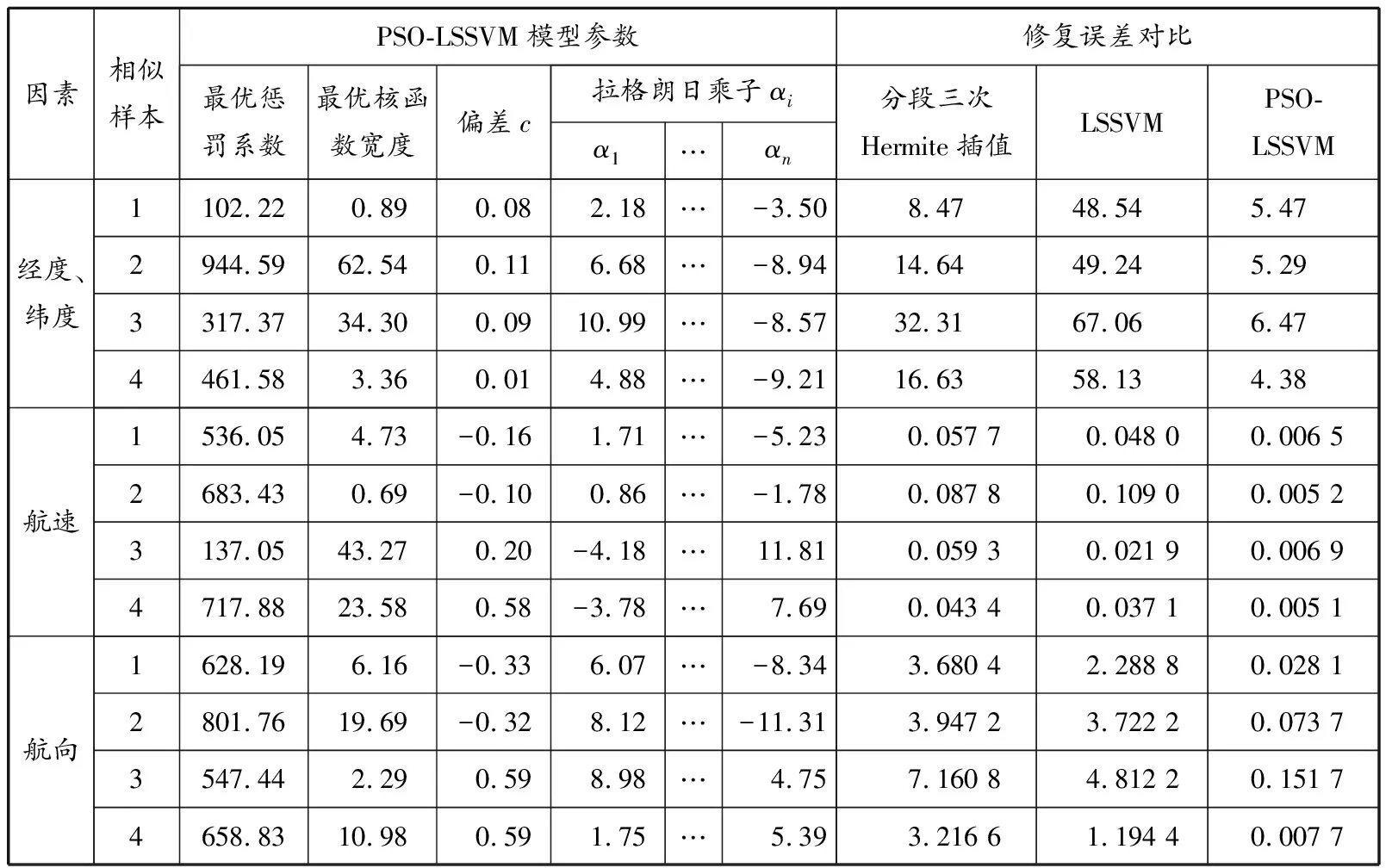
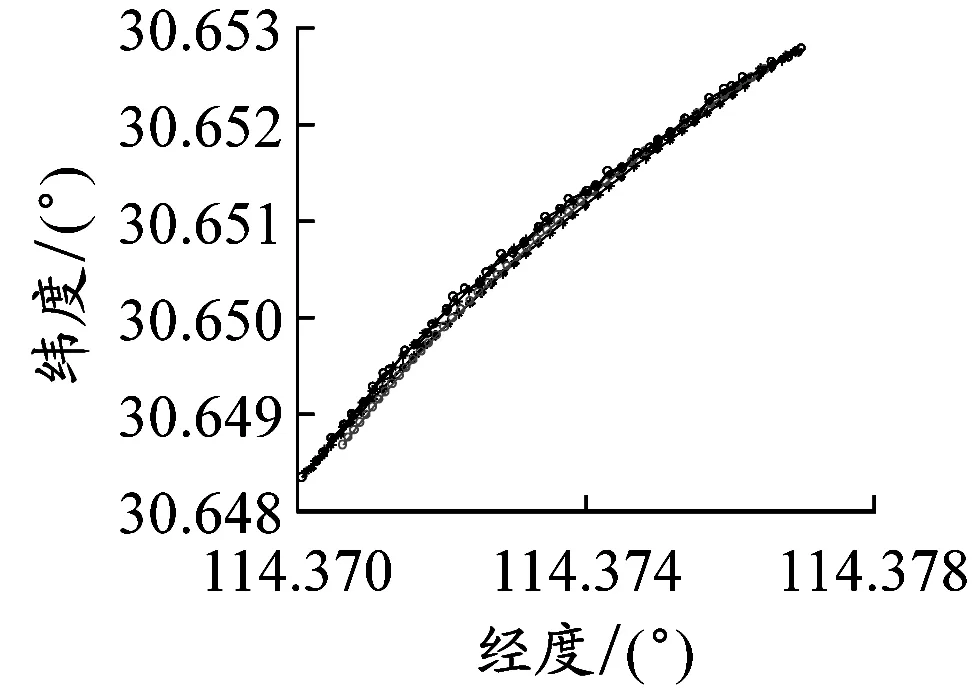
4.3 动态AIS数据修复

5 结 论
