基于齐次有限时间收敛的电控柴油机转速自抗扰控制方法

王源庆，苏娟，任光，张均东，于世永

(1.南通航运职业技术学院轮机工程系，江苏 南通 226010；2.大连海事大学轮机工程学院，辽宁 大连 116026)

0 引 言

电控柴油机推进控制系统建模过程中存在简化处理，建模理论和方法有诸多假设，所建模型必然存在偏差，导致控制系统有模型偏差、负载扰动的问题，常规依赖精确模型的控制算法的应用受到限制。在实船中，结构简单、稳定性好的PID控制仍占主导地位。[1]然而,在实船应用中当海况发生变化时，需要重新对控制系统参数进行整定，且要使转速能很好地跟随参考信号，就需要较大的比例增益系数，这会导致超调。另外,由于船用电控柴油机推进系统属于大惯性系统，当给定的转速阶跃较大时控制系统积分环节还会出现控制输入饱和现象，这些都使PID控制在实船应用中具有一定的局限性[2]。

文献[3]将自抗扰控制(active disturbances rejection control,ADRC)算法应用到船舶电控柴油机推进控制系统中。ADRC仅依赖于系统I/O数据，计算负担小，响应速度快，具有主动抗扰能力。然而,ADRC非线性误差反馈环节类似PD控制，控制效果有限,且ADRC常用非线性fal函数作为分段函数，参数多、调节困难且不利于理论分析和实际应用[4]。本文利用齐次有限时间收敛理论建立ADRC的误差反馈控制律——有限时间收敛的非线性误差反馈控制律(finite time-nonlinear state error feedback law,FT-NLSEF)[5],设计基于反双曲正弦函数的微分跟踪器(arsinh tracking differentiator,ATD)、基于反双曲正弦函数的扩张观测器(arsinh extended state observer,AESO)，减少控制系统调节参数，降低理论分析难度，有利于工业实际应用。最后，利用船用电控柴油机推进控制系统的平均值模型对基于齐次有限时间收敛的ADRC(FT-ADRC)算法的抗扰能力进行测试，并与自整定PID控制和常规ADRC的算法进行对比，验证FT-ADRC算法的优越性。

1 船用电控柴油机推进控制系统数学模型

本文以瓦锡兰7RT-Flex60C电控柴油机为研究对象，该柴油机最大持续功率为16 520 kW，额定转速为114 r/min。运用平均值模型法，建立电控柴油机推进系统转速控制方程[6]：

(1)

则式(1)可表示为

假设船用电控柴油机推进系统状态量为

则式(1)可以表示为

(2)

式中：f(x1(t),x2(t))+g(x1(t),x2(t))u(t)-b0u(t)通常被看作系统扰动总和的近似表达，且有界；b0>0；u(t)为系统控制输入；y(t)为系统输出。

2 FT-ADRC

2.1 ATD

ADRC采用非线性分段幂次函数fal(x)，实现状态量和扰动量的动态估计。fal(x)函数有分界拐点，在分界拐点附近存在控制波动，动态性能较差,且分段函数结构复杂、参数较多，控制系统的参数调节复杂[7-9]。因此，本文采用结构简单的反双曲正弦函数替代常用的fal(x)函数。

反双曲正弦函数的表达式为

(3)

由fal(x)函数与反双曲正弦函数arsh(x)的对比(见图1)和式(3)可知，反双曲正弦函数为奇函数，其导数为

(4)

图1也可以印证上述结论。因反双曲正弦函数光滑连续、调节参数少，本文用其代替ADRC常用的fal(x)函数，并通过仿真验证其性能。

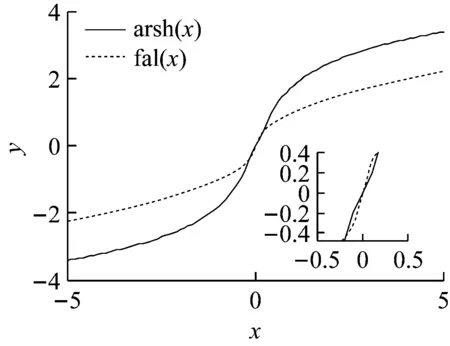
图1 函数arsh(x)与fal(x)的对比

对式(2)，利用反双曲正弦函数构造系统的二阶ATD:

(5)

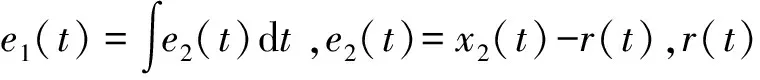
(6)

式中，T>0。

2.2 AESO

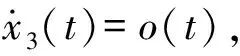
(7)

对式(7)利用反双曲正弦函数构建扩张观测器：

(8)

式中：β1,β2,β3>0。适当选取β1、β2、β3，由式(8)可以预估出式(7)中的所有状态变量x1(t)、x2(t)和x3(t)，即z1(t)→x1(t),z2(t)→x2(t),z3(t)→x3(t)。

系统的稳定性证明见文献[10]。

2.3 FT-NLSEF设计

(9)

由式(8)可得z3(t)=x3(t)。由文献[4]可知u(t)=(u0-z3(t))/b0，将其代入式(9)，船用电控柴油机推进控制系统控制误差变为

(10)

为改善控制系统的暂态性能，下面设计基于齐次有限时间收敛的反馈控制律。

式(10)可以被下列形式的误差反馈有限时间镇定：

u=-k1sigα1(x1)-k2sigα2(x2)

(11)

式中：k1,k2>0;α2∈(0,1)；α1=α2/(2-α2)。该系统为全局有限时间稳定。

由式(5)可知，ATD的参数有R、a1、a2和b，主要利用经验试凑法确定，与另外两个环节的设计相对独立。参数R是表征ATD响应速度的量，其值越大响应速度越快，但噪声抑制能力越弱，因此R取值在满足性能要求的前提下越小越好；a1的作用与R类似，其值越大跟踪速度越快，精度越高，但过大也会降低噪声抑制能力；a2主要影响微分特性，其值越大输出越平滑，但响应速度越慢；b的主要作用是微调ATD跟踪效果。

由式(11)可知，FT-NLSEF的参数有k1、k2和α1(α2可由α1得到)，k1、k2类似PD控制的比例增益和微分增益，α1为系统指数收敛系数。参数α1通过仿真试验调试设置，k1、k2采用文献[11]关于非线性误差反馈控制律参数整定的方法调节，描述如下：

k1=424.107 1/ts2,k2=1.343 3/ts

(12)

式中：ts为系统期望有限调节时间，ts=4.75/wc，wc为误差反馈控制律带宽。如果ts>0，则k1、k2均为正值，显然满足误差反馈控制律的稳定性条件。

对于AESO，为简化参数调节，易于工程实现，采用文献[11]关于非线性观测器的参数整定方法，描述如下：

β1=9veso,β2=27veso2,β3=27veso3

(13)

式中：veso为观测器观测速度，veso=1.5wc。因β1β2-β3=243veso3-27veso3，只要wc>0，就满足文献[10]观测器稳定条件：β1β2-β3>0。

参数b0为估计值，与实际值的误差通过观测器进行补偿。

3 结果分析

为验证本文算法的优越性，分别对自整定PID控制、基于fal函数的常规ADRC和FT-ADRC进行仿真研究，具体如下：

采用MATLAB/Simulink对3种控制方法进行仿真对比研究，在MATLAB/Simulink仿真环境下建立船用电控柴油机推进控制系统数学模型。对FT-ADRC，过渡过程和扩张观测器采用反双曲正弦函数建立，误差反馈采用齐次有限时间收敛反馈控制律，其原理见图2。

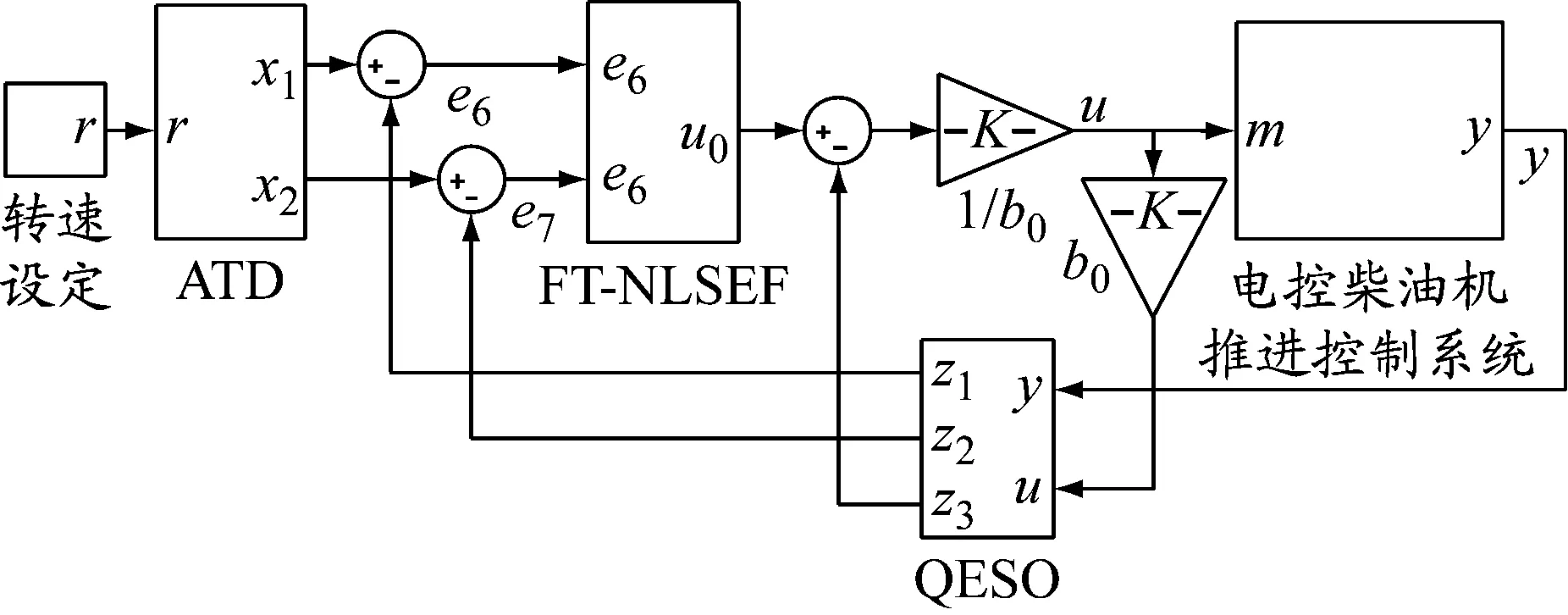
图2 FT-ADRC原理

由式(12)和(13)可知，FT-ADRC算法主要调节参数只有ts一个，较常规ADRC参数、自整定PID控制参数少，易于工程实现。

在仿真比较时，基于fal函数的常规ADRC算法控制原理同图2，算法结构如下：

x1(t)=x1(t)+T0x2(t)

x2(t)=x2(t)+T0fhan(x1(t),x2(t)-r(t),r0,h)

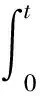
fe=fal(e3(t),α1,ε)

fe1=fal(e3(t),α2,ε)

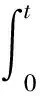
e7(t)=y(t)-r(t)

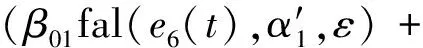
基于fal函数的常规ADRC算法中：主要调节参数为β1、β2、β3、β01和β02;其他参数中，T0为仿真步长,r0为速度因子(其值越大跟踪速度越快),h为滤波因子；fhan和fal函数由文献[8]得到。总体来说，常规ADRC参数较多，不利于实际应用。

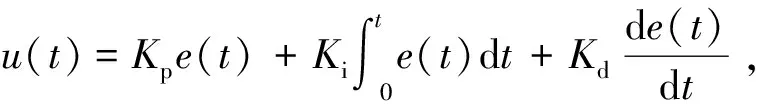
对进出港、超车和避让等船舶机动航行的工况进行仿真分析，不考虑风浪、船舶惯性等因素的影响。为清晰地展示仿真效果，仿真时间设置为100 s，给定柴油机初始转速为额定转速114 r/min，此后根据机动航行情况，30 s时驾驶台将转速设置为90.5 r/min，60 s时转速恢复至103.6 r/min。在这个过程中，螺旋桨负载转矩为1 390 kN·m。

对于基于BP神经网络的自整定PID控制，BP神经网络的结构为4-5-3，学习效率η=0.3，惯性系数α=0.05，权系数的初值取值区间为[-0.5，0.5]，Kp=180，Ki=2，Kd=10。

FT-ADRC参数设置为:R=10，a1=1,a2=1,b=0.3,α1=0.8,m=1,b0=1 000，ts=3。

基于自整定PID控制、常规ADRC和FT-ADRC的船用电控柴油机转速响应对比、转速误差对比、控制输入对比和输出扭矩对比见图3～6。

图3 船用电控柴油机转速响应曲线

由图3和4可知，船舶机动航行时，虽然FT-ADRC和传统ADRC参数未变，但是控制效果较好，表明ADRC方法的鲁棒性能优异。在转速阶跃控制时，3种控制算法中，FT-ADRC转速收敛最快，稳定时间小于5 s，而自整定PID控制最慢，稳定时间大于7 s。由图5和6可知，船舶机动航行时，FT-ADRC输入量、输出扭矩波动较传统ADRC、自整定PID控制的小。根据以上分析可知，FT-ADRC效果更好。

图4 船用电控柴油机转速误差曲线

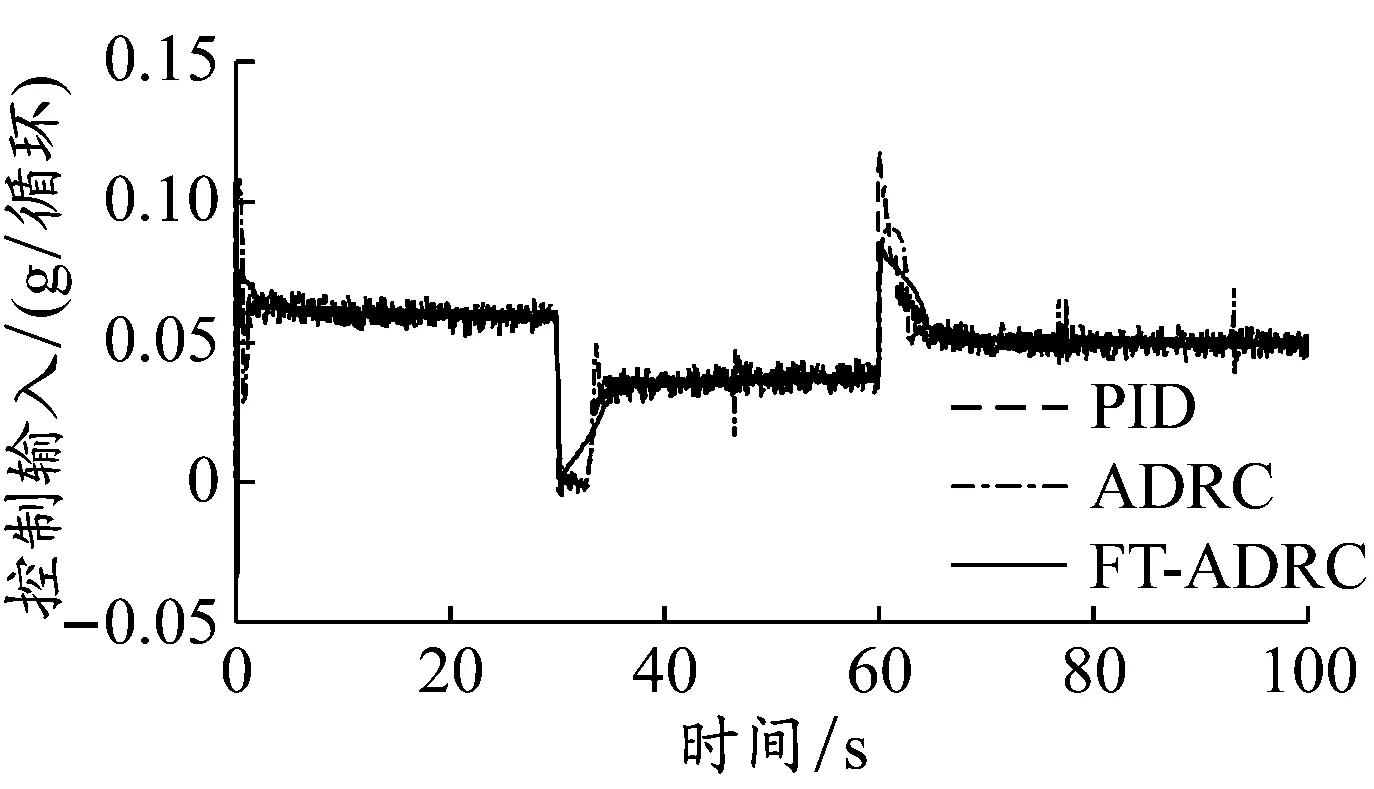
图5 船用电控柴油机控制输入曲线

图6 船用电控柴油机输出扭矩曲线

4 结束语

本文针对船用电控柴油机推进控制系统存在模型偏差、负载扰动问题，设计了基于齐次有限时间收敛的自抗扰控制(FT-ADRC)方法。首先，针对自抗扰控制(ADRC)常用的fal函数参数较多的特点，设计了反双曲正弦函数，建立了基于反双曲正弦函数的微分跟踪器(ATD)和基于反双曲正弦函数的扩张观测器(AESO)、利用反双曲正弦函数为奇函数的特点，使ATD和AESO的稳定性证明简单易行。其次，利用齐次有限时间收敛理论，建立了自抗扰的齐次有限时间收敛的非线性误差反馈控制律FT-NLSEF，并进行了有限时间收敛性证明。最后，通过对基于fal函数的常规ADRC、自整定PID控制和FT-ADRC的对比研究发现，基于FT-ADRC的船用电控柴油机调节参数少、转速响应快、控制输入和输出扭矩波动较小，证明了FT-ADRC算法的有效性。