基于GM(1,1)-MLP神经网络组合模型的物流总额预测
2019-01-08张乐汪传旭
张乐,汪传旭
(上海海事大学经济管理学院,上海 201306)
0 引 言
物流行业已成为社会发展的重要组成部分。相比物流运输量等物流类指标,物流总额是经济、生产水平、交通运输等指标的综合体现,精确预测物流总额的未来变化趋势,对企业和政府制定物流规划决策具有重要意义。
对于预测问题,多层感知器(multilayer perceptron,MLP)虽然拟合精度高[1-6],且对非线性问题处理能力强,但因缺乏新的预测样本,从而只能对以往数据进行训练和预测,预测结果缺乏实际意义。为预测基于时间序列的研究对象的未来变化趋势,国内外学者常采用灰色模型(GM)进行预测。党耀国等[7]建立无偏非齐次灰色预测模型NGM(1,1,k),并通过算例验证了该模型的有效性和实用性;王正新[8]利用改进的GM对中国高技术产业未来产出进行了预测;王龙等[9]基于信息熵和GM(1,1)对上海市城市生态系统演化进行了预测;YU等[10]建立了基于GM(1,1)的税收预测模型;XU等[11]利用一种新的灰色预测模型对中国未来电力消耗进行了估计;RAJESH[12]利用GM对供应链的绩效弹性进行了预测。然而,上述灰色预测模型主要通过研究自身随时间的变化规律从而实现对未来的预测,需假设其他影响因素在未来的变化较小,且对所研究的对象无影响,这在实际问题中是很难实现的。
本文将GM(1,1)与MLP神经网络组合,既能对未来数据进行预测,又能考虑其他因素变化对预测对象的影响,提高预测精准度:首先利用GM(1,1)对物流总额的影响因素进行预测,得到神经网络训练的新样本;然后通过神经网络对以往数据进行学习获得网络参数值,建立神经网络模型;最后将新样本导入已完成学习的网络模型中,得到全国物流总额预测值。本文选取中国国家统计局(http://www.stats.gov.cn/)1996—2016年相关指标数据对未来十年的全国物流总额进行预测。
1 全国物流总额预测模型的建立
1.1 GM(1,1)
常见的时间序列预测主要包括灰色预测、线性拟合和非线性拟合等。其中,灰色预测既能拟合变化趋势不明显的小样本指标,又能对线性增长、指数增长等其他变化趋势明显的指标有良好的拟合效果。当指标数量较多时,若直接对指标进行曲线拟合,则需要逐个选择每个指标对应的逼近函数,较为烦琐,而采用灰色拟合可免去此过程。本文中主要指标的变化趋势多呈现指数增长或线性增长,符合灰色预测使用条件,故采用GM(1,1)的指标预测比采用其他方法的指标预测更精准、更高效。
灰色系统理论是邓聚龙教授在19世纪80年代创立的,GM是灰色系统理论的一部分。GM(1,1)表示该预测模型为1阶、变量为1个。利用该模型对全国物流总额的影响因素进行预测。假设每个影响因素数据为
X(0)={x(0)(1),x(0)(2),…,x(0)(21)}
(1)
将原始数据累加,生成数列:
X(1)={x(1)(1),x(1)(2),…,x(1)(21)}
(2)

(3)
将计算得到的a和u代入一阶线性微分方程,得到
再通过累减还原运算得到原始数列。GM(1,1)为
(1-ea)(x(1)(1)-u/a)e-ak
(4)
1.2 基于共轭梯度优化的MLP结构
MLP是一种前馈人工神经网络,具有良好的非线性拟合功能,其3层结构见图1。
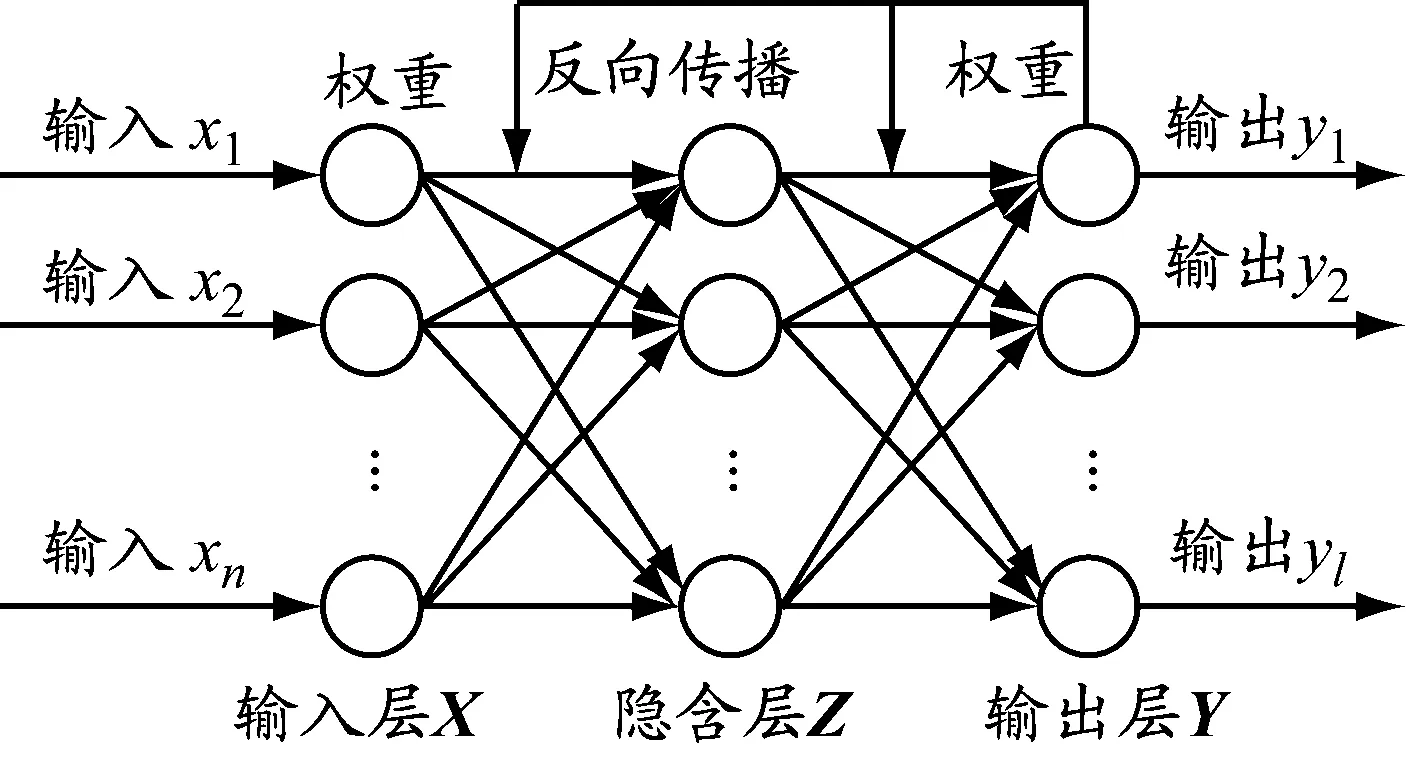
图1 MLP结构
MLP包括输入层、隐含层(一个或多个)和输出层,可用数学表达式描述为
(5)
式中:输入层X=(x1,x2,…,xi,…,xn),隐含层Z=(z1,z2,…,zj,…,zk),输出层Y=(y1,y2,…,ym,…,yl);wij为输入层第i个神经元与隐含层第j个神经元之间的连接权,wjm为隐含层第j个神经元与输出层第m个神经元之间的连接权;f1为隐含层的激活函数;f2为输出层的激活函数;θj和γm均为阈值。
MLP学习过程就是依据训练样本不断通过反馈来调节连接权和阈值,直至满足停止条件。根据训练好的连接权和阈值计算新的输入样本即可得到预测值。本文设置隐含层数量为1,选Sigmoid函数为激活函数:
Sigmoid(x)=1/(1+e-x)
(6)
常见的最优参数反馈调节算法有误差逆传播法(即BP算法)、共轭梯度法和拟牛顿法等。标准的BP算法存在易陷入局部极小值问题;共轭梯度法允许解向非最小梯度的方向寻优,这样就有机会收敛到全局最优解,且该算法运算量不大、收敛速度快。
1.3 GM(1,1)-MLP组合预测模型
步骤1确定物流总额影响因素。基于GM(1,1),根据原始数据X(0)=(x(0)(1),x(0)(2),…,x(0)(21))对影响因素进行预测,结果为
(7)
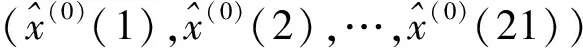
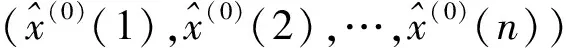

步骤4对预测结果进行误差分析。令误差为d,定义其表达式为
(8)
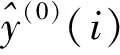
2 全国物流总额预测
选取国内生产总值(GDP),居民消费价格指数,全国进出口总额,货物运输量,社会消费品零售总额,全社会固定资产投资,人口数量,第一产业增加值,第二产业增加值,第三产业增加值,交通运输、仓储和邮政业增加值,以及法人单位数等12个指标作为全国物流总额影响因素[13-15]。根据1996—2016年的数据对2017—2026年全国物流总额变化进行预测。
2.1 GM(1,1)预测物流总额影响因素
收集1996—2016年12个物流总额影响因素的数据,采用GM(1,1)对物流总额进行预测。社会消费品零售总额原始数据见表1。
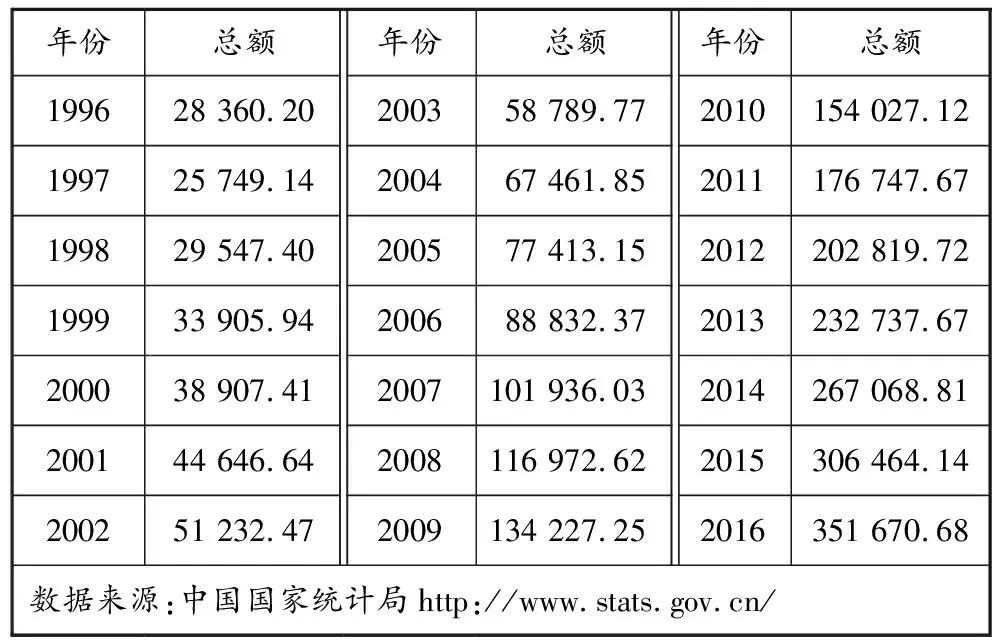
表1 1996—2016年社会消费品零售总额 亿元
社会消费品零售总额,货物运输量,交通运输、仓储和邮政业增加值,以及人口数量的2017—2026年预测结果见图2,其他8个物流总额影响因素的预测值由于版面有限不在此处列出。
从图2可以看出:虽然用GM(1,1)预测会带来一定的误差,但该模型对数据适应性较强,拟合效果仍较好;由于在模型训练阶段采用影响因素拟合值和物流总额真实值共同完成神经网络学习,两者间形成了新的映射关系,不会改变物流总额影响因素对其的作用效果,GM(1,1)所造成的误差对最终预测结果的影响被大大减弱,对物流总额的预测精度比在模型训练阶段仅采用影响因素真实值完成神经网络学习的更高。
2.2 MLP预测物流总额
以1996—2016年12个物流总额影响因素的拟合数据为输入向量,1996—2016年全国物流总额原始数据为输出向量进行神经网络训练,在(0,1)范围内随机初始化网络中的所有连接权和阈值。为有效减少过度学习对训练结果的影响,将训练组和检验组按7∶3的分配比例进行检验。输入层、隐含层和输出层神经元个数分别设置为12、7和1,培训类型选择批处理,优化算法为共轭梯度法,训练过程中初始λ设置为0.000 000 5,初始θ设置为0.000 05,间隔中心点设置为0,间隔偏移量设置为±5。
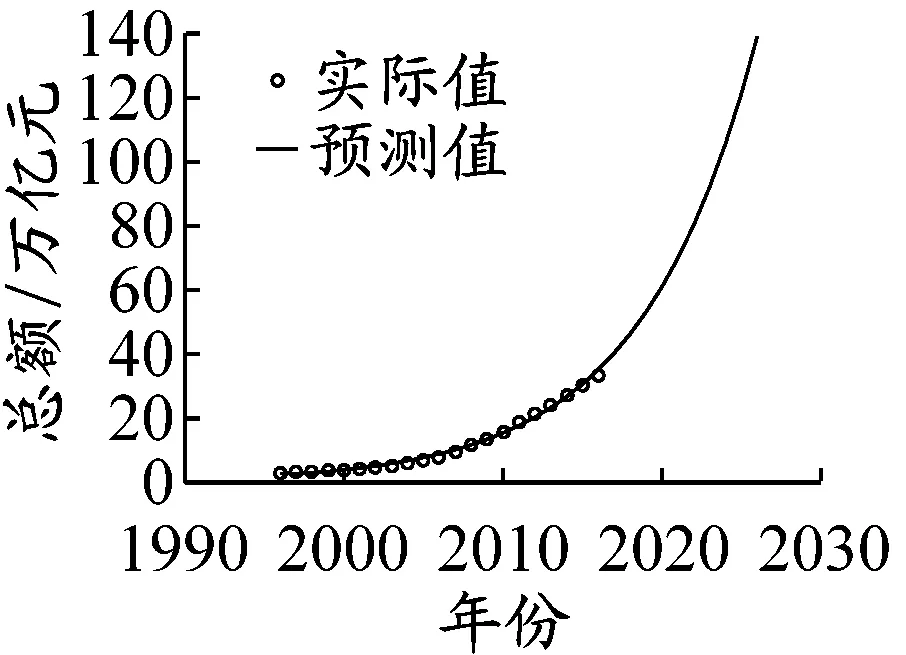
a)社会消费品零售总额
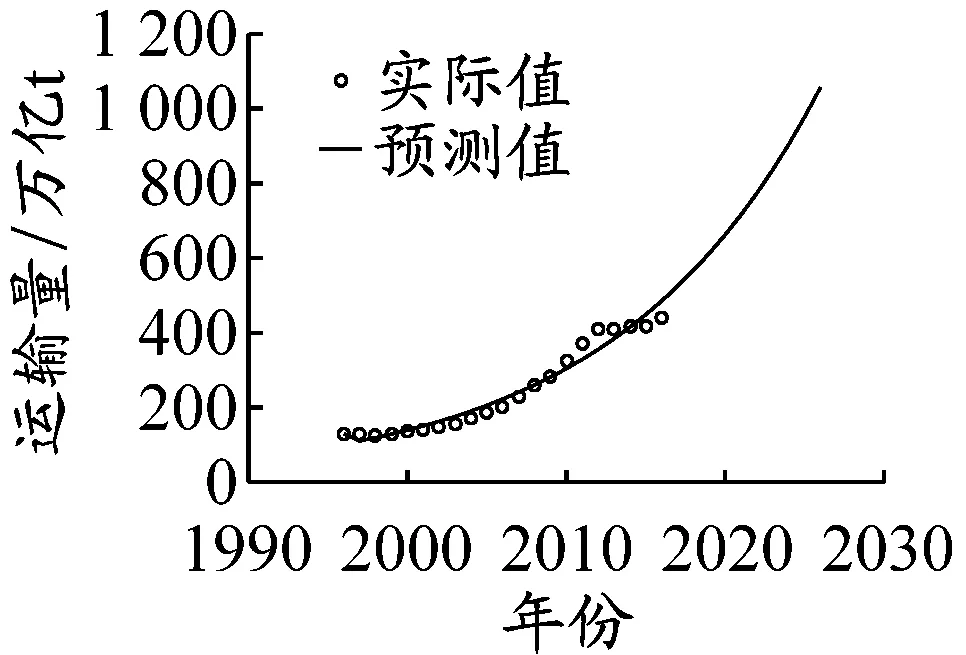
b)货物运输量

c)交通运输、仓储和邮政业增加值d)人口数量
图24个物流总额影响因素预测
在满足学习停止条件后,得到网络模型的连接权、阈值等模型参数,训练效果见图3。其中,训练组误差平方和为0.29,检验组误差平方和为0.11,真实值与预测值基本处在直线y=x上,训练效果较好。
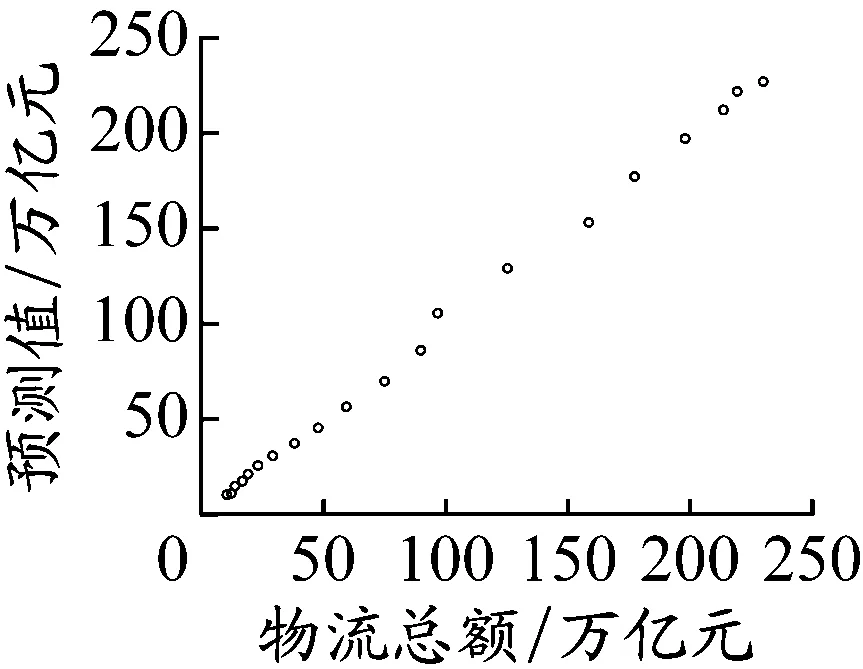
图3 MLP训练效果
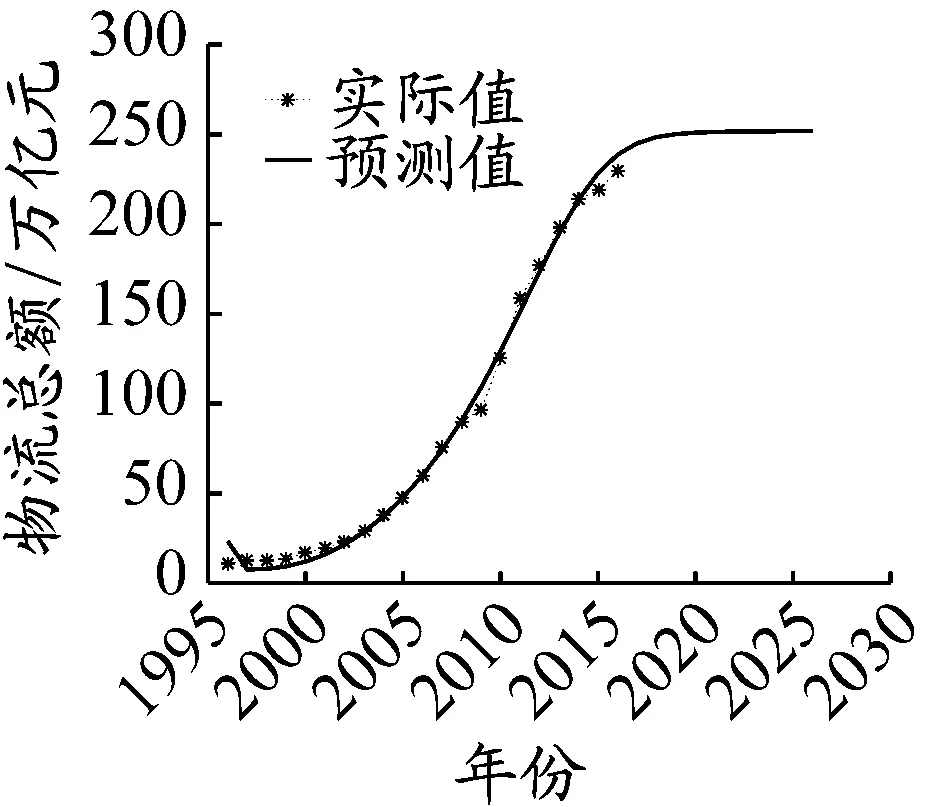
图4基于组合模型的全国物流总额预测
将2017—2026年12个物流总额影响因素预测数据(新样本)输入上述已完成学习的神经网络模型中,得到1996—2026年物流总额预测值,结果见图4。
从图4可以看出:2017—2021年全国物流总额增速虽然下降,但仍有较大增长空间;2021年以后物流总额趋于稳定,在252万亿元左右保持轻微增长。2017—2026年全国物流总额预测值见表2。
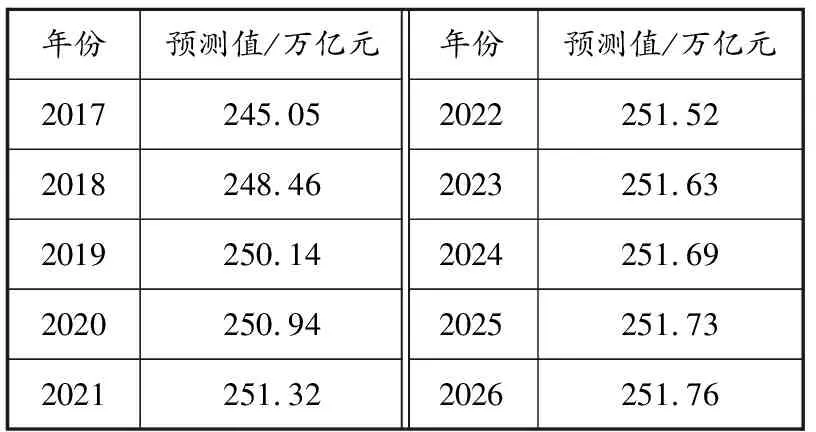
表2 2017—2026年全国物流总额预测值
2.3 预测结果检验
利用式(8)对组合模型与GM(1,1)近5年拟合结果进行比较,结果见表3。表3中拟合值1为基于GM(1,1)-MLP组合模型的拟合结果,拟合值2为基于GM(1,1)的拟合结果。从表3可以计算得出,基于组合模型的全国物流总额预测平均误差为2.3%,远小于基于GM(1,1)的预测平均误差25.2%。

表3 全国物流总额2012—2016年的预测模型拟合结果比较 万亿元
3 结 论
预测全国物流总额的变化趋势,对物流决策规划具有重要意义。采用GM(1,1)-MLP组合预测模型预测1996—2026年全国物流总额,发现2012—2016年物流总额拟合平均误差仅为2.3%(远低于用GM(1,1)预测的物流总额拟合平均误差25.2%),可有效应用于我国未来的物流总额预测。
在模型改进方面,由于MLP隐含层数设置为1层,而1次输出映射的能力有限,所以可以增加神经网络隐含层数量,进行深度学习,通过多层逐次映射后输出变量与输入变量的联系更密切,神经网络预测精度更高。
从预测结果看,2017—2021年全国物流总额数值仍有较大上涨空间,依然处于快速发展期,之后增幅缓慢趋于稳定,相关企业和政府可适当加大物流行业投入,抓住发展机遇。在物流规模达到稳定后,物流行业会向着规范化、高效化方向发展,企业和政府可根据自身需求提前制定相关策略。
