一种超高自由度的稳健调零实现算法研究*

张 伟 岳鹏飞 梁 楠 李剑凯 张 萍

1.河南省科学院应用物理研究所，郑州 450008 2.河南省物联网感知技术与系统重点实验室，郑州 450008 3.北京北斗星通导航技术股份有限公司，北京 100102

阵列天线技术广泛应用于雷达、声呐、天文和无线通讯等领域[1-3]。该技术通过权矢量的更新，主瓣对准期望信号方向，在干扰的到达方向上形成零点，以对消掉空间干扰。在实际应用中，环境、信源和阵列传感器等存在误差[4]，假设期望信号的导向矢量与真实信源导向矢量失配,导致阵列波束形成器把期望信号当作干扰来加以抑制，称为信号的自相消。针对高自由度的空频二维宽带处理器[5-6]，提出一种超高自由度的稳健[7-9]调零算法，进行空频矢量不确定集约束，约束期望信号不受损失，最小化阵列的输出功率，理论分析得出矢量不确定集加载量的取值范围，实现空频宽带处理器SYSTOLIC阵列的最优权值求解过程。提出算法对于空频二维导向矢量随机误差[10-11]具有一定的稳健性，且对期望信号的功率变化不敏感，有效改善了空频自适应调零算法的输出信干噪比。计算机仿真验证了理论分析的正确性和算法的稳健性。

1 空频自适应处理

存在N个远场的宽带信号si,i=1,2,…，N(包括期望信号和干扰)，以θi,i=1,2,…，N方向入射到空间M元均匀线阵上，通常假设第1项s1对应于感兴趣的期望信号，而si,i=2,…，N对应于N-1个干扰信号。

(1)

其中，τmi表示第m个阵元上接收的第i个信号的延时；nm(t)为第m个阵元通道的热噪声。

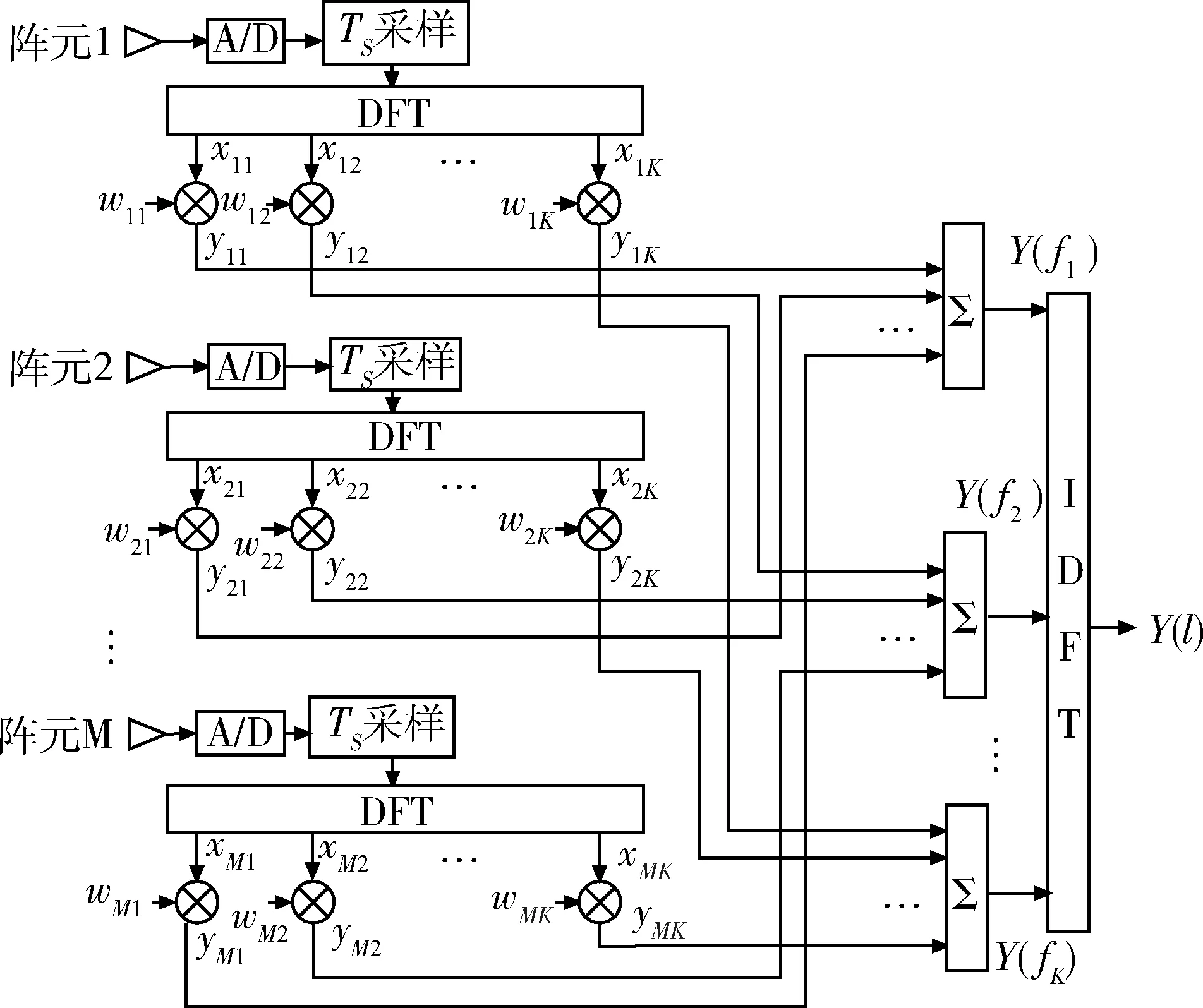
图1 空频自适应处理器结构图

宽带信号可以通过傅里叶变换分为若干个频点，对每个频点按窄带波束形成的方法进行处理。实际上，由K点离散傅里叶变换(DFT)把宽带信号在频域上划分为K个窄子带，并对每一个窄子带进行窄带波束形成，然后把波束输出转化为时域输出。

空频自适应处理器结构如图1所示，建立宽带信号模型：

X(fk)=A(fk)S(fk)+N(fk)k=1,2,…,K

(2)

(3)

式中，X(fk)，S(fk)，N(fk)分别为对应某频率的接收数据矢量、信号矢量及噪声矢量的离散傅立叶变换，带宽为B的信号通过DFT划分为K个子带；a是对应带宽内频点的空频二维导向矢量。

X(fk)=[x1k,x2k,…,xMk]Tk=1,2,…,K

(4)

用M×1维向量w(fk)表示对应于接收数据fk子带的处理器权矢量，则

w(fk)=[w1k,w2k,…,wMk]Tk=1,2,…,K

(5)

则，空频二维处理器的滤波输出信号为

(6)

2 超高自由度的稳健调零实现算法

超高自由度调零算法包括3个部分：分析滤波器组(AFB)、子带信号空域处理和综合滤波器组(SFB)，如图2所示。

超高自由度调零算法是将中频AD数据通过窗函数与FFT完成并行下变频处理，完成了分析滤波器的快速实现。分析滤波器由频谱搬移、窄带滤波及抽样组成；综合滤波器由插值、滤波与频谱搬移组成。为了便于后端对子带信号的处理，采用并行转串行处理完成不同子带信号的串行顺序输出。窗函数越长子带带宽越窄，子带内通道失配越小，干扰功率谱泄露越小。所以较长的窗函数对干扰抑制度有好处，但是系统资源消耗变大，实际工程中要对资源与性能进行折中。

图2 多通道分析与综合滤波器架构

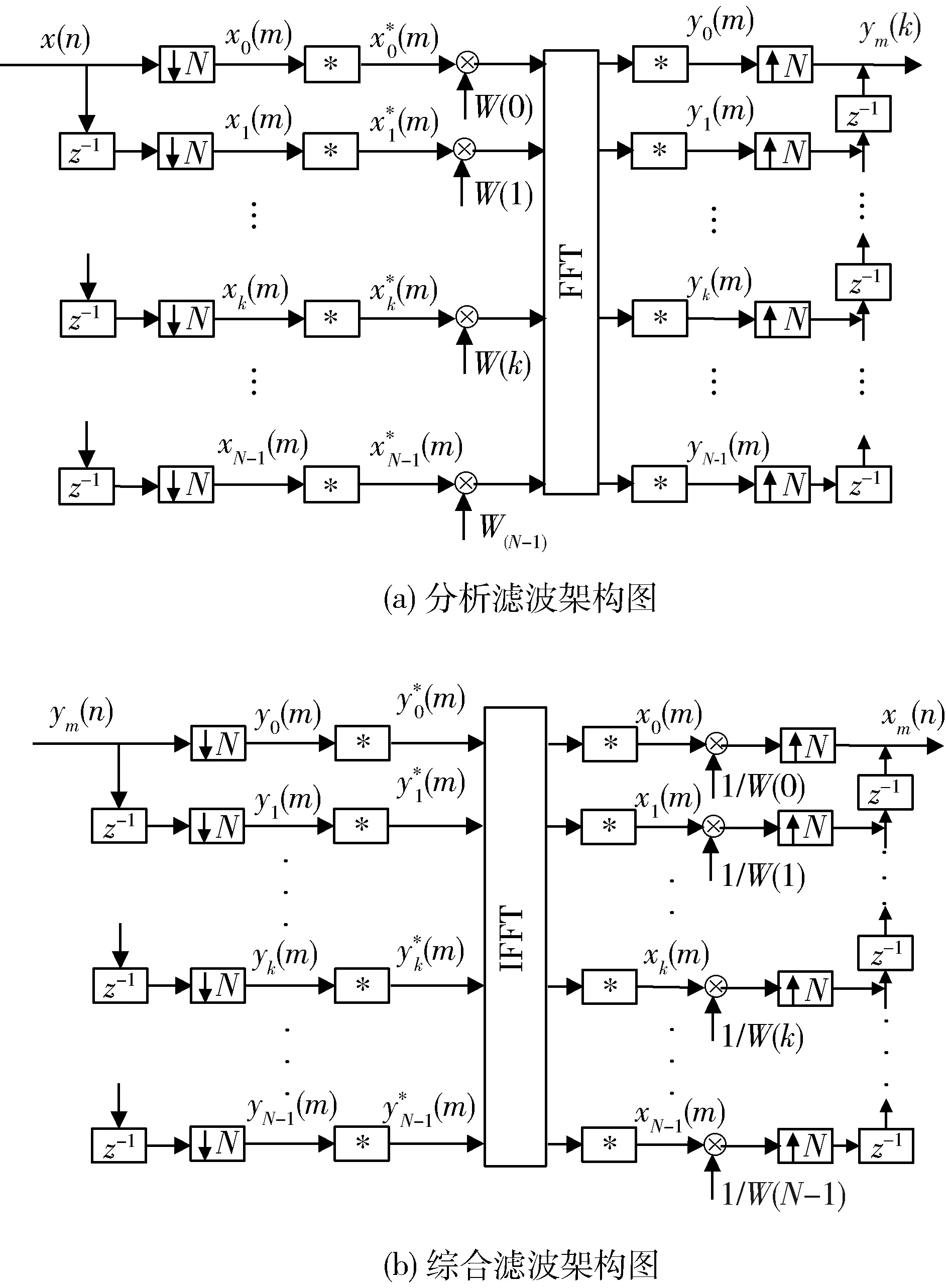
图3 基于窗函数实现分析、综合滤波器架构图

子带信号空域处理部分将fk频点的子带信号在球形约束下搜索真实期望信号的空频导向矢量，从而使期望信号输出功率达到最大，表示为

(7)

(8)

(9)

(10)

(11)

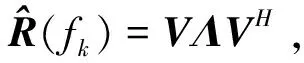
(12)

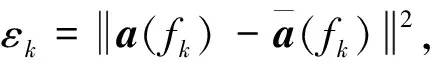
(13)

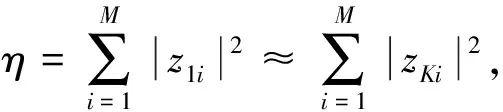
3 性能仿真

使用标准Capon波束形成算法[10-15]与本文提出的超高自由度的稳健调零算法进行分析讨论，分别讨论算法对快拍数的稳健性和算法对指向误差的稳健性。

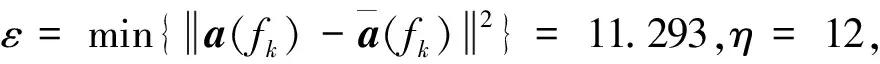
图4 同样快拍数下2种算法方向图比较

当快拍数目较少时，标准Capon波束形成算法不能在期望信号方向上形成主瓣，旁瓣电平比较高，但可以有效抑制干扰。经过超高自由度的稳健调零算法处理后的宽带波束在期望信号方向上形成高增益，降低了旁瓣电平，与标准Capon算法相比，旁瓣电平降低了5～10dB，改善了系统信噪比，充分证明了本文算法具有较好的鲁棒性。

图5给出了2种算法的输出信干噪比随指向误差变化的曲线。期望信号波达方向是0°，宽带干扰波达方向是-40°，输入信噪比为-20dB,输入信干比为-80dB。估计期望信号的导向矢量与真实信源导向矢量失配指向误差从0°～8°变化，当存在期望信号的指向误差时，本文算法改善了系统输出信干噪比，随着指向误差增大，本文算法仍保持一定的稳健性。

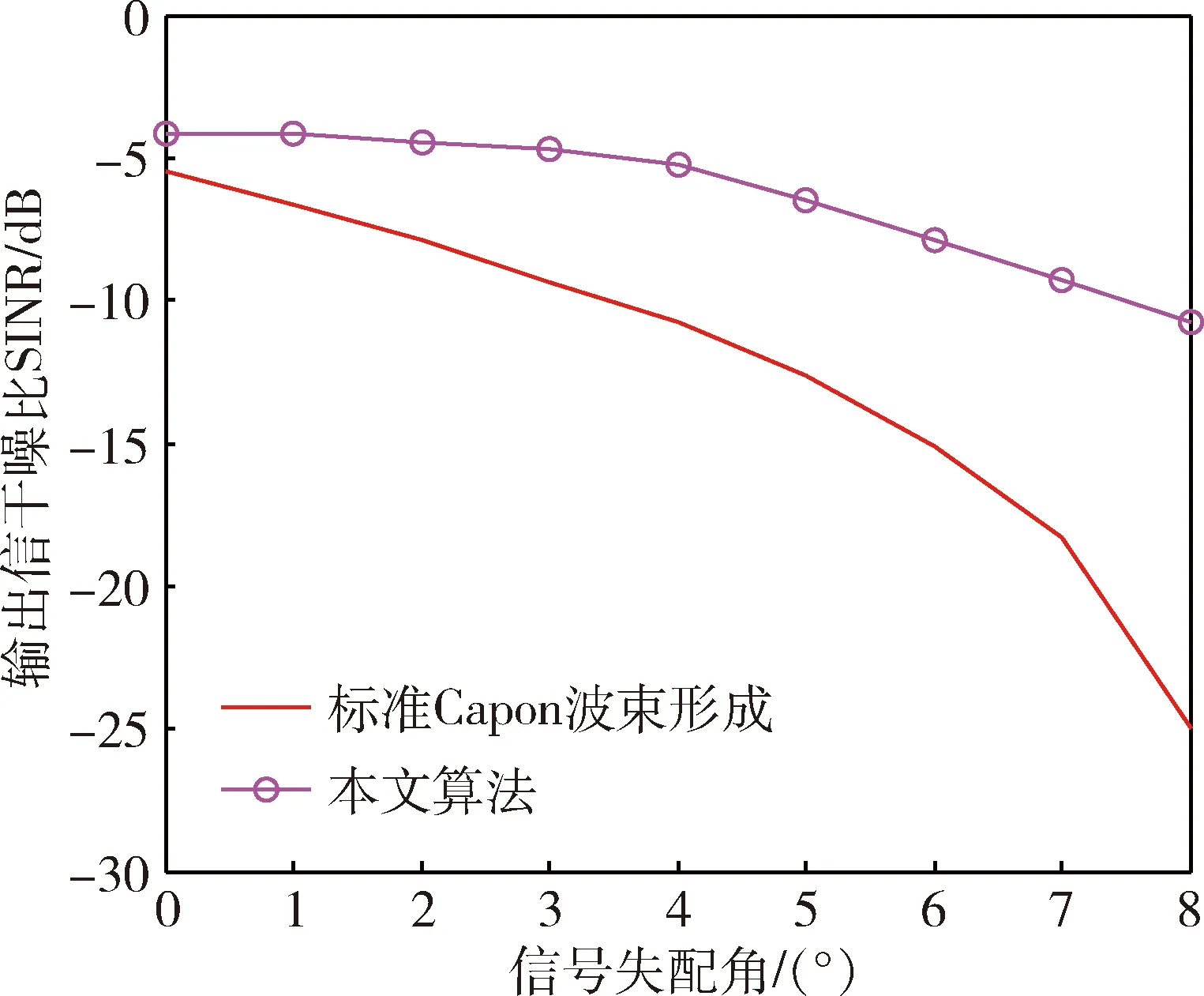
图5 输出信干噪比随指向误差变化的曲线

4 结束语

针对高自由度的空频二维宽带处理器，提出超高自由度的稳健调零算法，理论分析得出矢量不确定集加载量的取值范围，实现空频宽带处理器SYSTOLIC阵列的最优权值求解过程。算法对期望信号的功率变化表现出不敏感的特性，有效改善了空频自适应调零算法的输出信干噪比。计算机仿真验证了理论分析的正确性和算法的稳健性。