基于AR模型的MEMS惯导随机误差分析方法
2019-01-07吕春红
吕春红 李 洋 赵 坤 董 纯
北京航天自动控制研究所,北京 100854
随着MEMS技术的不断发展和成熟,一些低成本的炮弹、导弹和火箭弹等武器需要采用低成本的惯性器件实现自主导航。但问题是MEMS惯性器件的精度低,各项性能指标不能达到导航系统的要求,因此,为提高MEMS捷联惯性导航系统精度,需要对现有惯性器件的误差特性进行深入研究并建模,采用切实有效的补偿方法加以消除。MEMS惯导工具误差一般可分为静态、动态和随机误差项。静态和动态误差一般认为是与载体运动的速度、加速度等有关的确定性误差项,可通过试验标定补偿。而随机漂移是陀螺的重要特性,国内外在陀螺漂移测试及建模方面做了大量工作。从陀螺的质量块、弹簧系统等谐振结构层面建立MEMS陀螺仪的数学物理模型,然后对误差进行补偿,虽能取得较好的效果,但是在大多数情况下,由于缺乏MEMS陀螺制造结构等相关信息,大都采用时间序列统计建模等方法。其中Allan方差法是对陀螺噪声进行分析的标准方法,它可以将各种误差源及其对整个噪声统计特性进行辨识。除此之外,还可采用神经网络[1]、小波分析[2]等对陀螺的随机误差进行建模。文献[3-5]给出了一般陀螺的随机误差典型Allan方差分布。
结合实际工程应用,描述了根据MEMS惯导输出,采用时间序列分析方法,对陀螺进行趋势项、平稳性检验及周期检验,然后采用基于Allan方差估计出MEMS陀螺主要随机误差项,建立AR模型,通过Kalman滤波对随机误差进行估计与补偿。
1 时间序列分析方法
陀螺的随机漂移一般是时间的函数,实际上是一个随机过程。对于随机过程,我们无法用时间t的确定性函数来加以描述。但是,可以借助数理统计方法,通过对大量漂移数据的统计分析,找出它的统计规律或者统计特性。
时间序列分析方法将平稳、正态和零均值的随机序列看作是各时刻相关的序列,序列由各时刻出现的白噪声组成,即k时刻为:
xk=φ1xk-1+φ2xk-2+…+φnxk-n-
θ1ak-1-θ2ak-2-…-θmak-m+ak
(1)
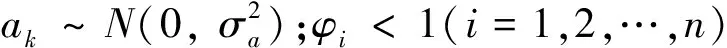
如果模型中θi=0(i=1,2,…,m),则模型简化为:
xk=φ1xk-1+φ2xk-2+…+φnxk-n+ak
(2)
该模型称为n阶自回归模型AR(n)。如果模型中φi=0(i=1,2,…,n),则模型简化为:
xk=ak-θ1ak-1-θ2ak-2-…-θmak-m
(3)
该模型称为m阶的滑动平均模型MA(m)。
2 陀螺漂移数据预处理
ARMA模型要求数据{xt}是平稳、正态和零均值的时间序列。陀螺输出的原始信号中一般包含有缓慢变化的趋势项和随机漂移项。所以在采用时间序列分析法进行建模前,一般需将原始信号中的趋势项去掉。
2.1 基于二次拟合的趋势项提取方法
一般趋势项可以采用线性、指数等函数进行拟合。本文采用二次拟合的方法,趋势项的函数如下:
mt=a0+a1t+a2t2
(4)
其中,a0,a1,a2为待估参数。
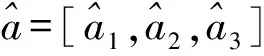
(5)
也可用差分法消除趋势项。一阶差分算子定义为:
▽xt=xt-xt-1
(6)
二阶差分定义为:
▽2xt=▽(▽xt)=xt-2xt-1+xt-2
(7)
实际问题中往往需要差分的阶数很低,一阶或两阶就已经足够。
2.2 平稳性检验
平稳性检验是陀螺随机漂移数据检验的首要问题,它用来检验漂移数据序列是否具有不随时间推移而变化的统计特性。本文采用逆序法进行平稳性检验。首先设定每个子样的个数l为20,原始序列的长度为N,则子序列的长度为n=N/l。逆序总数的理论平均值为:
(8)
逆序总数的理论方差为:
(9)
通过对100个子序列进行计算,可以得出计算的逆序总数为651。利用构造的统计量计算出的u=0.6525。
从图1可以看出,各子序列的逆序数总体是呈线性递减的趋势,并且在真实逆序数的上下变化。当显著性水平为0.05时,若|u|<1.96,则说明是平稳序列。而上面计算出的u为0.6525,满足平稳序列的要求。
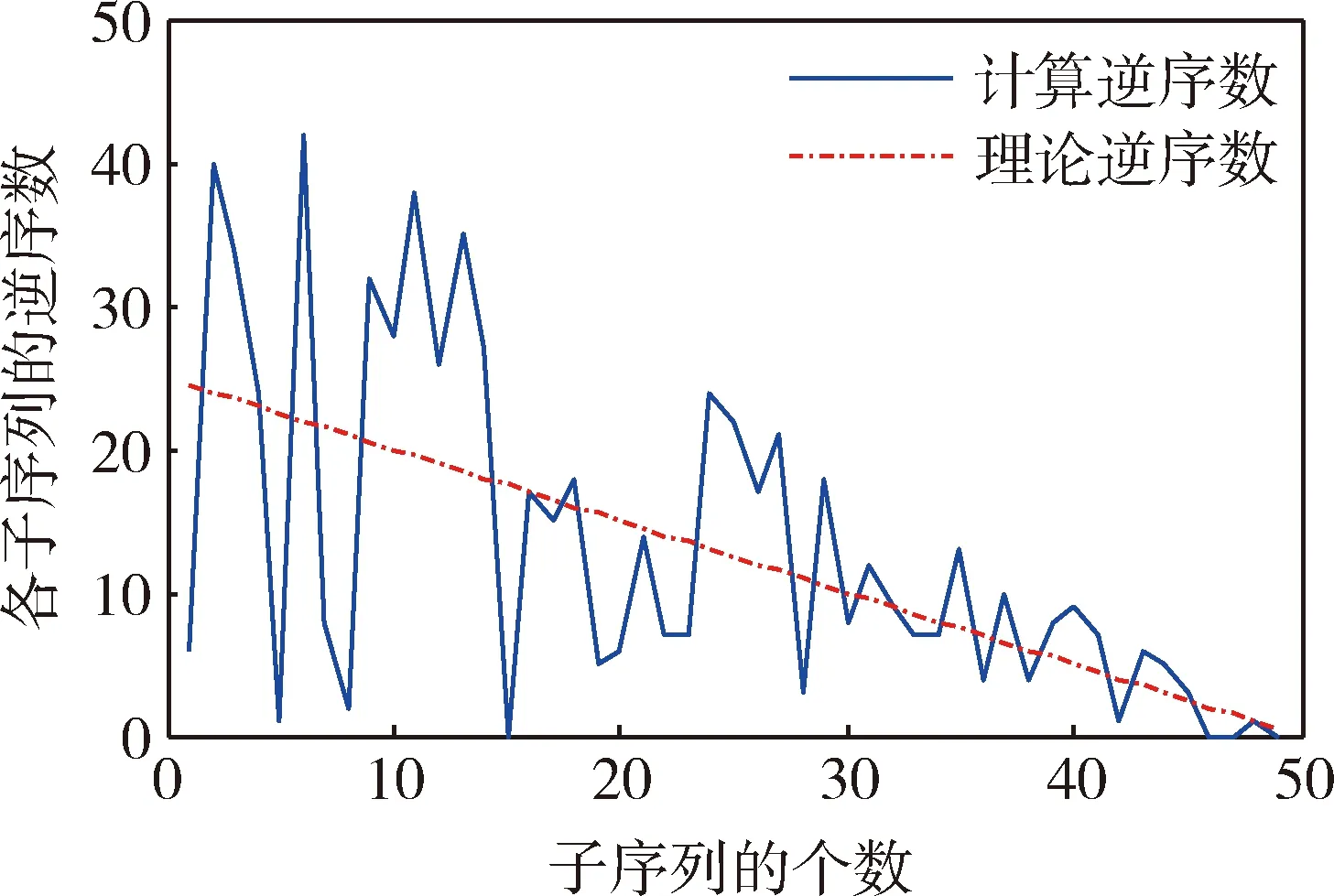
图1 各子序列的逆序数分布图
2.3 周期性检验
周期性检验用来识别陀螺随机漂移数据中是否包含有随机量以外的周期性分量,周期性检验的方法是直接考察从漂移数据得到的概率谱密度函数、自相关函数或功率谱密度的图形。从图2可以看出,功率谱密度图中也没有明显的谱峰,说明陀螺的输出中不包含有周期项。

图2 陀螺漂移的功率谱密度
3 基于Allan方差的随机误差估计
将MEMS惯组放置在试验室隔离地基上,测试轴置于水平面内东西方向,采样频率100Hz,采样3000s。MEMS陀螺的原始输出曲线图如图3。
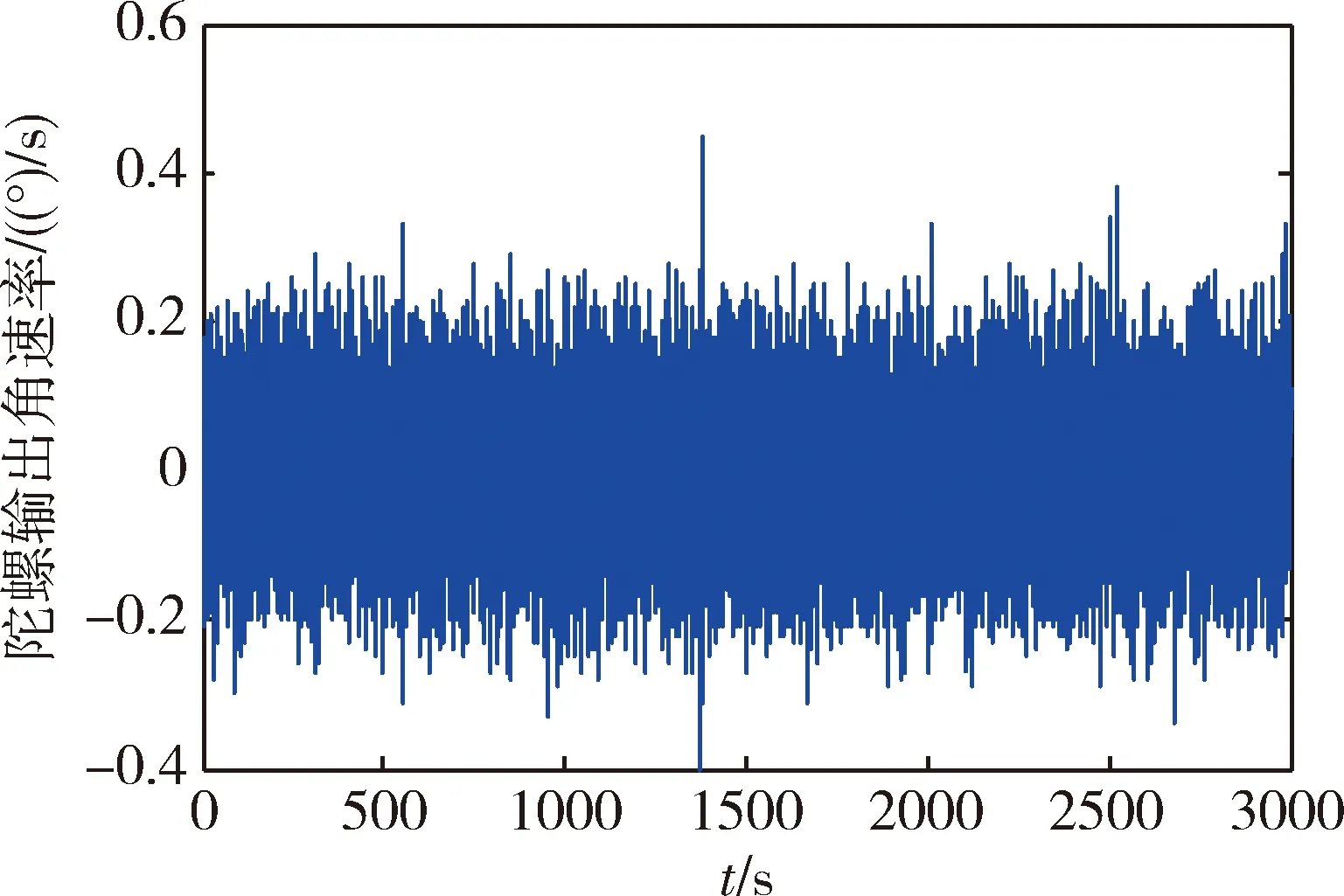
图3 MEMS陀螺静态输出曲线图
在陀螺随机误差中通常存在角随机游走,速率随机游走,偏差不稳定性,量化噪声和速率斜坡。根据上面对5项随机误差的分析,总的Allan方差可以表示为5项随机误差的Allan方差之和,形式如式(10)[6]。
(10)
根据陀螺静态测试数据,计算的Allan标准差与的双对数(log-log)曲线图如图4所示。
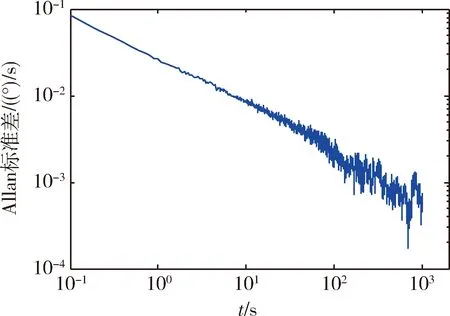
图4 MEMS陀螺的Allan标准差曲线图
对式(10)采用最小二乘拟合方法可计算得到角度随机游走系数、零偏不稳定性系数、速率随机游走系数、速率斜坡和量化噪声的估计值,如表1所示。

表1 MEMS陀螺的各项随机误差估计值
从表1可以看出,该陀螺的角度随机误差为MEMS随机误差中的主要部分,其他噪声项的系数非常小,可以忽略不计。
由于MEMS陀螺的随机漂移模型阶次比较低,一般不超过二到三阶,所以在实际建模中选用了AR(1)、AR(2)和AR(3)三种时间序列模型进行讨论。AR模型结构式可写成式(2)的形式。对各参数估计得到数据如表2所示。

表2 AR模型的参数估计结果
采用FPE(最终预报误差)准则分析模型定阶。从表中可看出,AR(3)模型的FPE最小,但与AR(1)模型的FPE基本相同,所以可采用AR(1)模型来描述陀螺的随机漂移模型。
上面已经确定出陀螺随机漂移模型的类型和参数,采用AR(1)进行建模。采用所建立的模型即可进行卡尔曼滤波。AR(1)模型如式(11):
x(k+1)=-0.3326x(k)+w(k)
(11)
其中,x(k)是陀螺漂移模型的状态,w(k)是均值为0,方差为σ2的白噪声。
建立的卡尔曼滤波状态方程如式(12):
x(k+1)=Φ(k,k-1)x(k)+Fw(k)
(12)
其中,Φ(k,k-1)=-0.3326,F=1。
系统的观测值可以表示为状态量加上白噪声:
y(k)=x(k)+v(k)
(13)
则H=1,V(K)为白噪声序列。
4 仿真实验
根据上述建立的随机误差AR(1)模型,建立Kalman滤波方程,进行陀螺输出随机误差估计。状态方程的噪声方差阵Q和观测噪声方差阵R取为AR(1)模型的估计误差的方差。滤波误差的协方差阵初值p(0/0)取为1,状态量的初始值x(0)取为0。图5为陀螺静止时采样1min的数据,采样频率为100Hz。
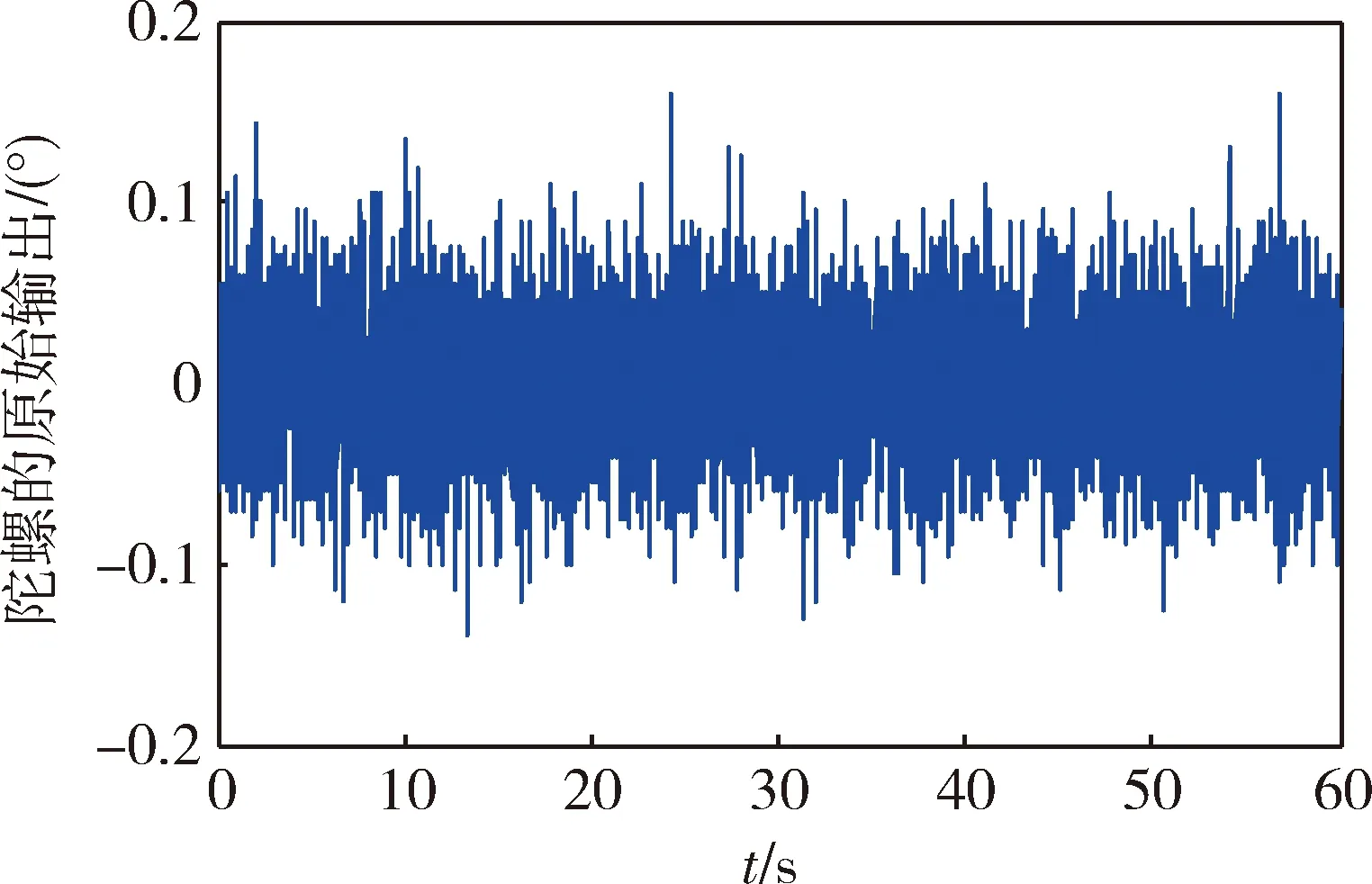
图5 陀螺输出的原始数据

图6 卡尔曼滤波后的陀螺输出
图6为Kalman滤波后的陀螺输出曲线。滤波前陀螺输出的原始数据的标准差为0.0143(°)/s,滤波后陀螺输出的标准差为0.00424(°)/s,提高了3倍。
5 结论
采用Allan方差法分析了陀螺中的各项随机误差系数,通过时间序列方法对随机误差进行建模,再应用Kalman滤波可以减小MEMS陀螺的随机误差。仿真实验表明采用时间序列分析进行参数估计可以有效消除MEMS惯组导航方程中的模型误差和测量误差,从而大大提高MEMS捷联惯导的精度。本文是根据静态测试数据进行随机误差建模,后续可以结合导弹当前运动模型,研究动态条件下MEMS惯导的随机误差建模与补偿方法。
