逆变器供电对永磁同步电机振动和噪声的影响
2019-01-07,,,
, , ,
(1.上海电力学院, 上海 200090; 2.国网江苏省电力公司金湖县供电公司, 江苏 金湖 211600)
永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)具有高效率、宽调速范围、高功率密度等良好的特性,已在电动汽车中得到了广泛应用[1-2]。电机的振动噪声会影响电动汽车的可靠性及舒适性,因此研究开发低振动噪声的车用PMSM具有重要的现实意义。
近年来,许多国内外学者对振动噪声进行了深入研究。上海大学黄苏融教授研究了PMSM电磁振动和噪声的估算方法及低噪声永磁电机的设计方法[3]。文献[4]应用解析法和有限元法相结合的方法,研究了内置永磁无刷直流电机的电磁振动特性,结果表明,定子电枢电流产生的径向电磁力对振动噪声的影响远大于永磁体产生的径向电磁力。文献[5]提出了一种基于模态分析计算电磁振动的方法,计算电磁力谐波在各模态频率下的振动幅值,其总和为电机总的振动。文献[6]研究了开关磁阻电动机、永磁电动机和感应电动机,提出应当充分考虑控制方式对电机噪声的影响。
本文首先建立2D电磁模型,将电流信号加入电磁力有限元模型中,通过有限元法计算逆变器供电电流和正弦电流作用下的磁通密度;然后,应用节点力传递法将电磁力耦合到定子齿上进行谐响应分析,研究样机在两种电流供电情况下的电磁振动和噪声频谱特性。
1 逆变器供电引入振动噪声源
1.1 样机电磁振动噪声计算流程
为了分析逆变器谐波对电动汽车PMSM电磁振动噪声的影响,本文以一台48槽8极45 kW电动汽车车用PMSM为研究对象,基于有限元法仿真分析车用PMSM的振动噪声特性。
本文样机多物理场耦合仿真的计算流程如图1所示。

图1 样机电磁振动噪声计算流程
1.2 逆变器引入电流谐波计算
由变频器驱动的电机,其电压和电流波形为非正弦波,电流谐波通过电枢反应对电机的电磁力波产生影响。其中5次、7次、11次、13次等谐波的作用尤为明显[7]。
根据麦克斯韦定律,PMSM径向电磁力波为
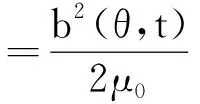
(1)
式中:b(θ,t)——径向磁通密度;
μ0——真空磁导率。
由定子l次电流谐波引起的定子ν次谐波磁动势为
fν(θ,t)=Fνcos(νpθ-lωt-φν)
(2)
式中:Fν——定子绕组ν次谐波磁动势幅值;
p——电机极对数;
ω——基波磁势角频率;
φν——ν次定子电枢谐波初相位。
转子永磁体磁动势为
fμ(θ,t)=Fμcos(μpθ-μωt)
(3)
式中:Fμ——转子永磁体μ次谐波磁动势幅值。
考虑l次电流谐波的气隙磁密表达式为
b(θ,t)=f(θ,t)Λ(θ)=
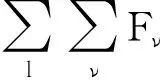
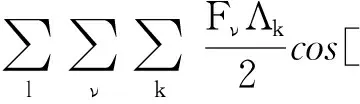
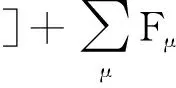
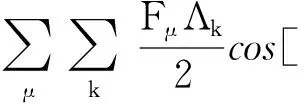

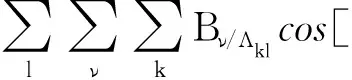
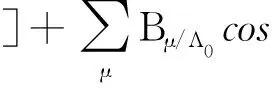

Bsl/Λ0l+Bsl/Λkl+Bpm/Λ0+Bpm/Λk=
Bsl+Bpm
(4)
式中:Λ0——平均磁导;
Λk——定子开槽磁导;
z——定子槽数;
Bsl——定子磁场;
Bpm——转子磁场。
此时,定子和转子磁场互相影响产生的径向力波为
(5)
由平均磁导调制的定子和转子磁场相互作用导致的电磁力波为
cos[(μ±ν)pθ-(μ±l)ωt-φν]
(6)
平均磁导调制的转子磁场和定子开槽磁场调制的定子磁场相互作用产生的电磁力波为
cos[(μp±νp±kz)θ-(μ±l)ωt]
(7)
定子开槽调制引起的转子磁场和平均磁导调制定子磁场互相影响产生的电磁力波为
Ppm/Λk-sl/Λ0l=
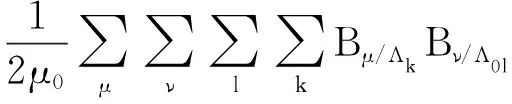
cos[(μp±νp±kz)θ-(μ±l)ωt]
(8)
由定子开槽磁导调制产生的定转子磁场互相作用引起的电磁力波为
(9)
径向力波特征参数如表1所示。表1中,fe=ω/2π=np/60;k为磁导谐波次数,k=1,2,3,…。

表1 径向力波特征参数
2 PMSM多物理场电磁振动噪声仿真计算
2.1 样机有限元仿真模型
样机结构技术参数如表2所示,2D电磁模型如图2所示。

表2 样机结构技术参数

图2 样机电磁有限元模型
2.2 样机电磁场有限元仿真
首先,应用MAXWELL软件对一台48槽8极车用PMSM样机进行瞬态计算,分别计算4 000 r/min额定运行时逆变器和正弦电流供电情况下的径向气隙磁密,并对磁密进行傅里叶谐波分解。这两种不同供电电流的A相电流波形如图3所示。由图3可知,样机采用逆变器供电时,电流中产生大量的电流谐波使波形出现了许多毛刺。
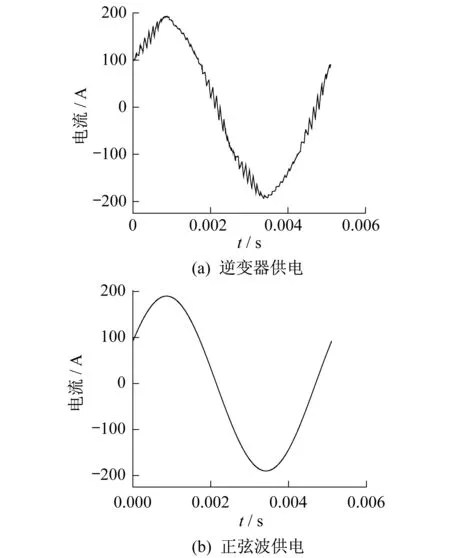
图3 两种电流源的A相电流波形
图4为逆变器供电时A相电流频谱图。由图4可知,逆变器供电时,PMSM的定子电流谐波分两个部分,一方面,在(6k±1)次谐波处辐值较大,如5次、7次、11次等;另一方面,在开关频率(10 kHz)附近有幅值较大的谐波电流。
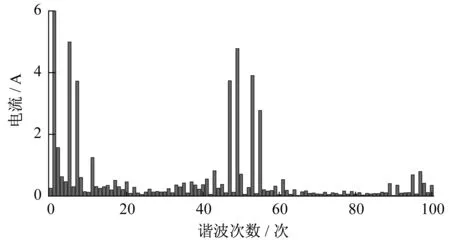
图4 A相非正弦电流频谱示意
分析得出逆变器供电时开关频率附近的主要电流谐波频率为
f=k1fc±k2f1
(10)
式中:fc——逆变器的开关频率;
f1——电机的运行频率;
k1,k2——奇偶性相异的正整数。
然后,利用有限元软件ANSYS计算样机在额定转速下不同电流供电时的二维瞬态电磁场。图5为样机在4 000 r/min运行时的径向气隙磁通密度随时间变化的波形图。由图5可知,与正弦波供电相比,逆变器供电时,运行时每个点的磁通密度幅值基本都增大了。

图5 径向气隙磁密波形
计算得到两种电流供电时的主要径向气隙磁密频谱如图6所示。由图6可知,与正弦波供电相比,逆变器供电时,一方面,气隙磁密在(6k±1)次的幅值均增加,在3次、9次、15次等处幅值均降低;另一方面,由逆变器引入的开关频率(即磁密谐波50次)附近的谐波幅值均增加。这表明在逆变器供电情况下,电枢反应导致的气隙磁场畸变程度较大。

图6 径向气隙磁密谐波对比图
3 样机振动和噪声特性分析
3.1 样机模态分析
图7为样机定子3D结构有限元模型。表3为考虑叠压系数及各向异性后样机的材料力学参数(表中材料力学参数是仿真时直接输入的参数值)。
图8为样机定子3D结构模态振型图。图8中,n代表径向模态阶数,m代表定子沿轴的两种振动形式。当m=0时,壳体同向振动;当m=1时,壳体反向振动[8]。其中径向模态是引起电机振动噪声的主要原因[9]。

图7 样机定子3D结构有限元模型

结构部件密度/(kg·m-3)弹性模量剪切模量Pa泊松比定子铁心0.95×7 800EX=EY= 2.1×1011,EZ=1.5×1011GXZ=GYZ= 7.3×1010,GXY= 8.0×10100.3

图8 样机定子结构模态振型
由文献[10]的分析可知,低次径向力波是引起电磁振动噪声的主要原因。因此,对于本文的48 槽8极电机振动噪声起作用的有效模态是0阶和8阶模态。
分析图8可知,对本文样机振动噪声起作用的有效模态是n=0阶固有频率8 497 Hz和9 538 Hz,以及n=8阶固有频率10 699 Hz和11 398 Hz。
3.2 逆变器谐波对PMSM振动和噪声特性的分析
为计算样机的电磁振动噪声特性,本文建立了样机电磁场和结构场多物理场强耦合电磁振动噪声有限元模型,如图9所示。
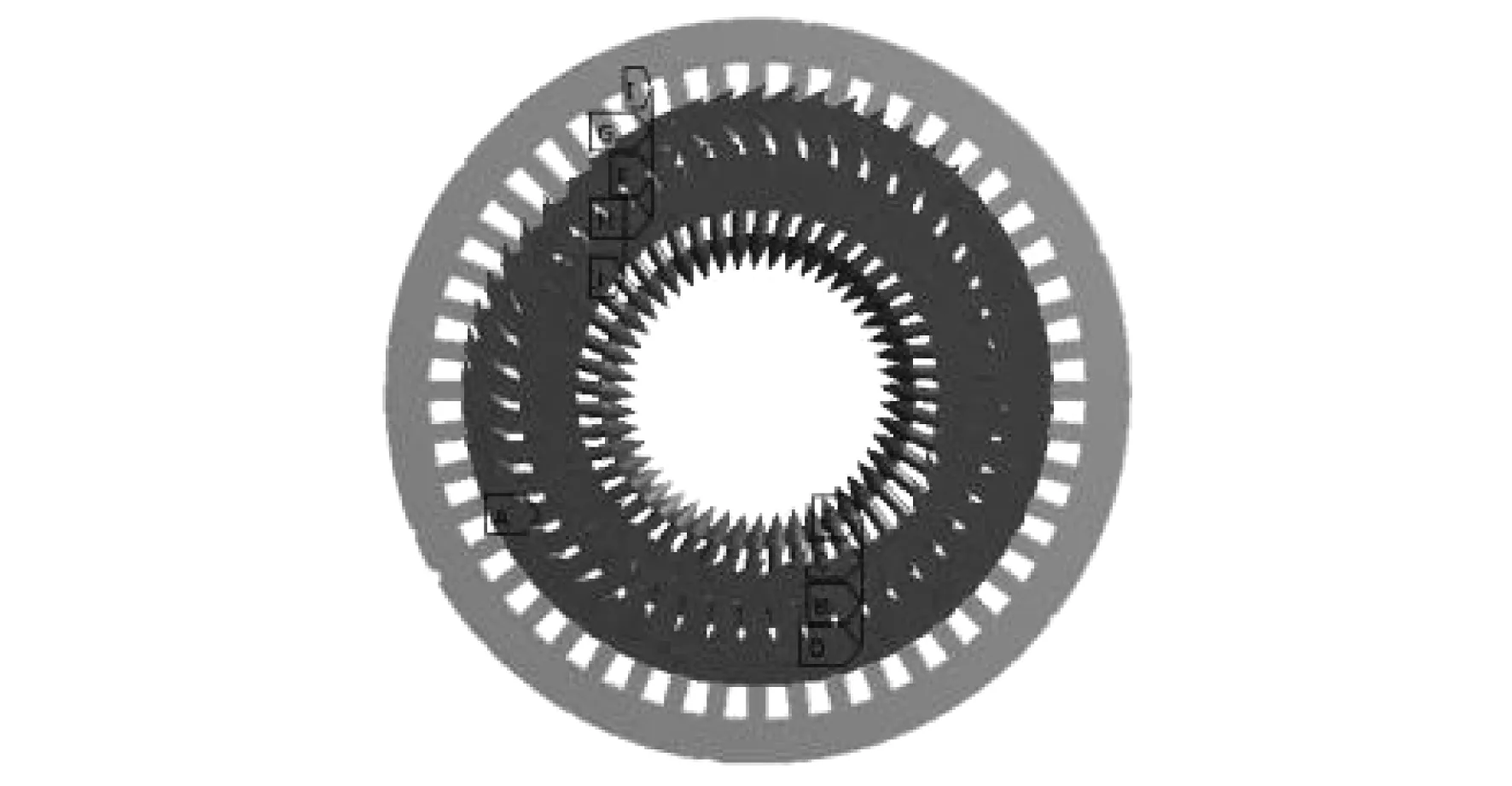
图9 样机电磁场和结构场多物理场强耦合模型
图10为两种电流供电情况下振动加速度频谱。对比正弦波供电,当逆变器供电时,振动幅值整体增加。不同电流供电下振动加速度的最大幅值点均出现在8 500 Hz,9 533 Hz,10 700 Hz,11 400 Hz附近,接近模态分析结果中0阶和8阶固有频率。开关频率10 kHz附近振动加速度增加较大,究其原因是引入逆变器开关频率的谐波电流加剧了高频段的结构共振。
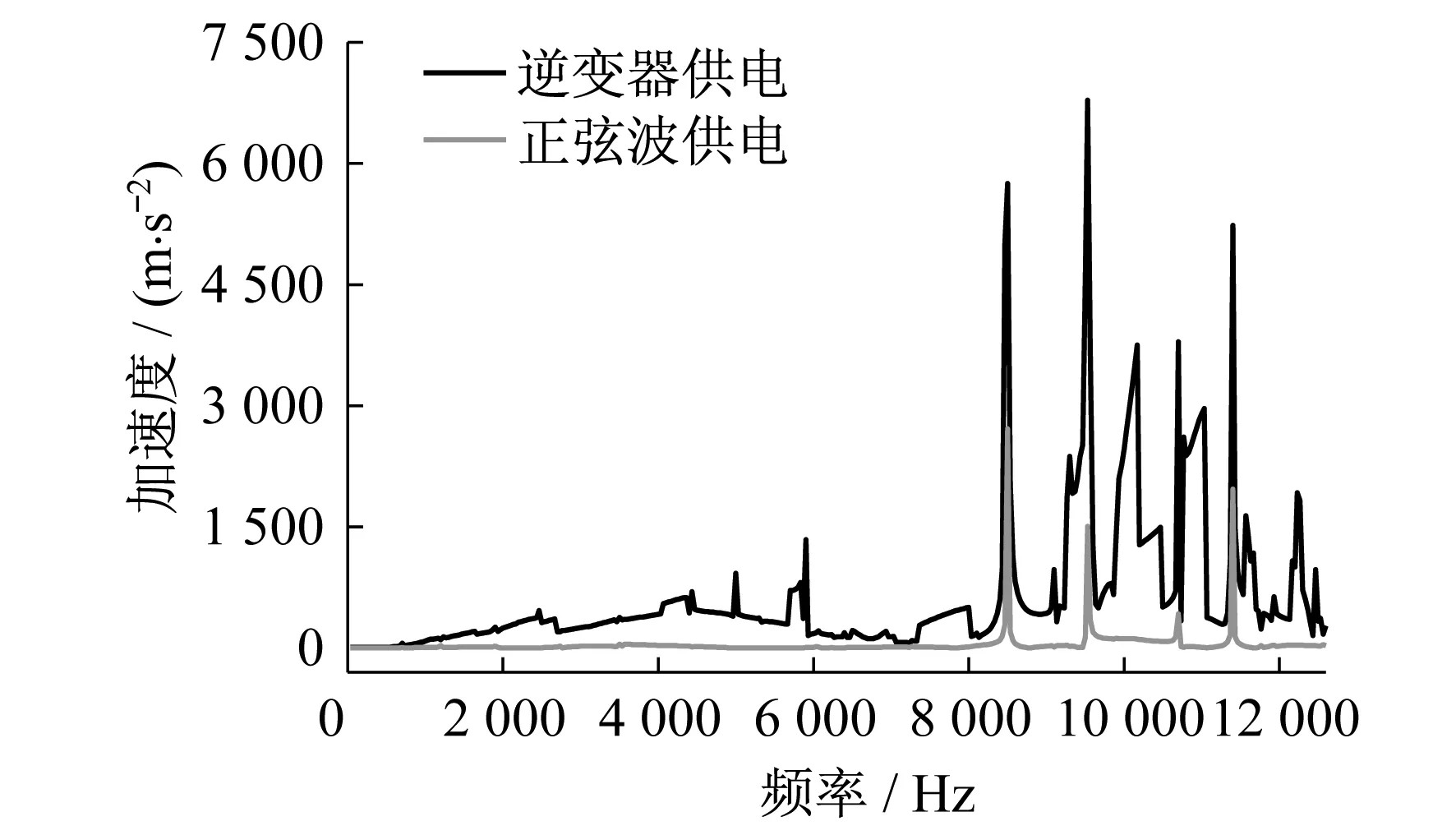
图10 两种供电情况下样机振动加速度对比
图11为两种供电情况下的电机噪声频谱。

图11 两种供电情况下样机电磁噪声对比
对比正弦波供电,当逆变器供电时,开关频率附近噪声增加较大,噪声的最大幅值点均出现在0阶和8阶固有频率附近,逆变器供电电流在0阶和8阶固有频率处的振动和噪声都大于正弦电流。
4 结 论
(1) PMSM采用逆变器供电时,电流和径向气隙磁密波形都出现许多毛刺,在开关频率附近存在幅值较大的电流谐波,增加了高频段结构共振的可能性。
(2) 逆变器供电引入了开关频率处的电流谐波,开关频率附近的电流谐波产生的径向气隙磁密幅值虽然较小,但仍会产生较大的电磁振动和电磁噪声。对于样机而言,开关频率附近的0阶和8阶模态频率处会出现振动噪声峰值。
