用于绕组变形检测的电力变压器集总参数等效模型研究
2019-01-07,
,
(上海电力学院 电气工程学院, 上海 200090)
电力变压器是发电厂和变电站的主要设备之一,在电力系统中承担着重要功能。其不仅造价比较昂贵,而且任何故障都有可能导致电力变压器中断运行,因此对电力变压器的保护以及在线状态检测是电力系统中最重要的问题之一[1-2]。
变压器绕组的变形和位移可能改变线圈弯曲部分的电压梯度。如果绕组变形或位移使得相邻两个线圈之间的间隙减小,则电压梯度可能更集中于弯曲处。电压梯度的增加不仅会破坏绕组间的绝缘从而导致故障,而且还会让线圈周围的温度升高,从而加快绕组绝缘的降解速度。此外,在充满变压器油的变压器中,温度升高会改变变压器油的性质,并可能导致局部放电,进而形成不良气体[3]。目前,常用的监测方法有热故障监测、油色谱分析、局部放电测量、传递函数、松弛电流以及恢复电压测量等,每种方法运用于特定类型的问题[4]。除了绕组故障检测外,确定故障的类型、位置和程度也非常重要:了解故障的类型、位置和程度,可以不断地监测故障状态,并确定变压器的停运风险;确定故障的类型和位置,可以让维修更容易、更快,从而可以提高变压器运行的经济性。
上述研究的关键点就是电力变压器等效网络的仿真计算。这也是系统研究电力变压器绕组机械故障(径向变形和轴向位移)和内部电气故障(匝间短路故障和局部放电故障)的故障程度以及位置对变压器差动保护影响的重点之一。本文通过建立集总参数模型,可以仿真绕组变形位移以及匝间短路故障,以期后续对故障类型、故障程度以及故障位置的检测提供参考。
1 变压器集总参数模型
电力变压器等效模型的建立需要充分考虑准确度,但同时也要考虑计算的复杂性。目前,电力变压器绕组模型主要有黑盒模型、物理模型和混合模型。混合模型是由黑盒模型和物理模型相结合而产生的。黑盒模型不适用于绕组位移的建模,因为其仅表示变压器在其端子上的行为[5]。本文针对物理模型中的集总参数模型进行分析,并给出当绕组发生轴向位移或径向变形时主要元件参数的改变及其求解方法。
1.1 拓扑结构
变压器物理模型能够具体反应变压器的绕组故障。当变压器发生绕组故障时,变压器集总参数模型上的参数也会随之改变,从而能够很好地反映绕组变形以及内部匝间短路故障。考虑到仿真的复杂性以及准确性,选取合适的绕组单元数建立模型[6]。
图1为双绕组电力变压器的绕组集总参数模型。主要由电阻、电感、电容及电导等元件组成,分别表征绕组及铁心的有功损耗、电磁效应、介质损耗及电容效应。
该模型可以有效地反映变压器的各绕组状态。变压器绕组变形包括轴向位移和径向变形,在变压器正常运行状态下,即绕组不发生任何变化时,模型中的各参数数值可通过解析法和有限元分析法取得[7-9]。当变压器处在故障状态时,模型的拓扑结构不改变,只是相对应的等效单元上的相关元件参数发生变化。在绕组发生变形的情况下,通过建立形变绕组模型来求取各参数。
1.2 数学表达
假设高压绕组侧有m个节点,低压绕组侧有n个单元,则高低压绕组各有m-1和n-1个单元。考虑到模型的精确性以及计算的复杂性,应选取合适的单元数。每一个单元对应于多匝层式或饼式绕组,而具体线匝的数目根据最高激励频率以及变压器绕组的几何尺寸来确定,以保证流过绕组单元线匝的电流基本恒定。
如图1所示,基本的梯形单元由电阻电感串联支路(阻抗支路)以及电导电容并联支路(导纳支路)组成。对于不同参数和结构的变压器而言,模型的拓扑结构是相同的,不同的只是高低压绕组侧的单元数目以及对应于具体元件参数的计算方法。
假设U=[uh1,…,uhi,…,uhn,ul1,…,ulj,…,ulm]分别表示各高低压绕组单元的节点电压,总共有m+n个节点,即高低压绕组单元共有n+m-2个,则阻抗支路电流共有n+m-2个,即I=[ih1,…,ihi,…,ihn-1,ul1,…,ilj,…,ilm-1],电流的正方向规定为流出其关联节点的方向。串联阻抗支路(串联电阻和电感支路)的各支路间通过阻抗支路电流相连,则串联阻抗支路Z和并联导纳支路Y可分别表示为
Z=R+jωL
(1)
Y=G+jωC
(2)
式中:G——电导。
Z和Y的矩阵表达式分别为

注:Rpei,Rpej—高低压绕组单元与油箱之间的绝缘电阻;Cii,Cij—高低压绕组单元的对地电容;hi,lj—高低压侧的节点;Ki,Kj—高低压绕组各单元间的串联电容;Rpi,Rpj—高低压绕组各单元之间的绝缘电阻;Rsi,Rsj—高低压绕组各单元的欧姆电阻;Chlij—高低压绕组之间的电容;L—自感;M—互感。uhi-1,ulj-1—hi-1和lj-1节点的节点电压;ihi,ilj—流过高低压绕组单元阻抗支路的支路电流。
图1变压器绕组集总参数模型
(3)
(4)
式(4)中,Yii为连接到节点i的导纳的总和,Yij为节点i和节点j之间导纳总和的相反数。
并联导纳支路为集总参数模型中电容和电导并联支路的等效,其支路之间的关系通过节点电压相连。其中
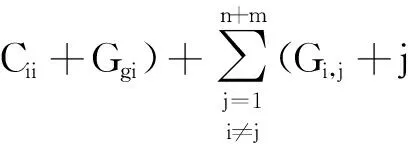
(5)
式(5)中的电导为图1中所对应电阻的倒数。
基于基尔霍夫电流和电压定律可得
YU=AI+B1
(6)
ZI=ATU+B2
(7)
其中,B1(nV×1),B2(nI×1)分别为输入电压和输入电流;A为关联矩阵且具有0,1,-1元素。
由此可得电压和电流为
U=(Y+AZ-1AT)-1(AZ-1B2+B1)
(8)
I=Z-1(-ATU+B2)
(9)
变压器绕组集总参数模型可以表示为
(10)
2 变压器绕组常见故障
变压器绕组的常见故障有径向变形、轴向位移以及内部匝间短路故障等。解体短路损坏的变压器发现,故障特征多表现为在故障电流所产生的轴向力和径向力的作用下,绕组扭曲、倾斜、坍塌和鼓包等永久性失稳变形。若不能及时发现,累积效应会使变形进一步加剧,进而导致绝缘损坏,出现匝间短路、饼间击穿、主绝缘放电等故障[10]。各种故障引起的绕组几何形状的任何变化都将导致图1所示的变压器等效电路的电容和电感元件发生改变。
2.1 绕组径向变形
径向变形形状以及程度分类如图2所示。

图2 高压绕组径向变形形状和程度分类
与绕组线圈的刚度相比,变压器绕组内侧的支撑结构(绝缘撑条)具有更明显的刚度。当承受轴向磁场产生的径向力时,导线在每个跨距之间或在轴向支撑结构之间的交替跨距处发生弯曲,形成了典型的梅花状。
变压器绕组径向变形主要影响的是集总参数模型中的高低压绕组之间的电容。根据实际情况的调查以及对绕组电动力的研究发现,这类故障主要发生在高压绕组的外侧。随着故障程度的增加,高压绕组与油箱之间的电容会减小。根据文献[8]的分析可知,径向变形绕组模型为

(11)
式中:r——绕组完整状态下的半径;
θ——径向变形程度角;
p,c——变形处所对应的深度和宽度。
通过重复改变式(1)中函数的范围,其余3种不同程度的变形即可表示出来。通过对绕组径向变形程度模型的建立,即可求取变形后的变压器绕组参数。在绕组变形的情况下,电场为不均匀分布。
并联电容(接地电容或绕组之间的电容)的计算式为
(12)
式中:ε0,ε1——介电常数。
2.2 绕组轴向位移
图3为高压绕组的轴向位移示意。
当高压绕组发生轴向位移时,会改变高低压绕组之间的互感以及高低压绕组间的电容数值。但文献[3,8]的研究表明,当发生相同程度的轴向位移时,电容的变化量不到1%,而高低压绕组之间互感的变化量超过10%,即互感的变化量数级为电容变化量数级的10倍以上。由此可知,在研究变压器绕组轴向变形时,可以忽略电容的变化量,只考虑互感的变化。
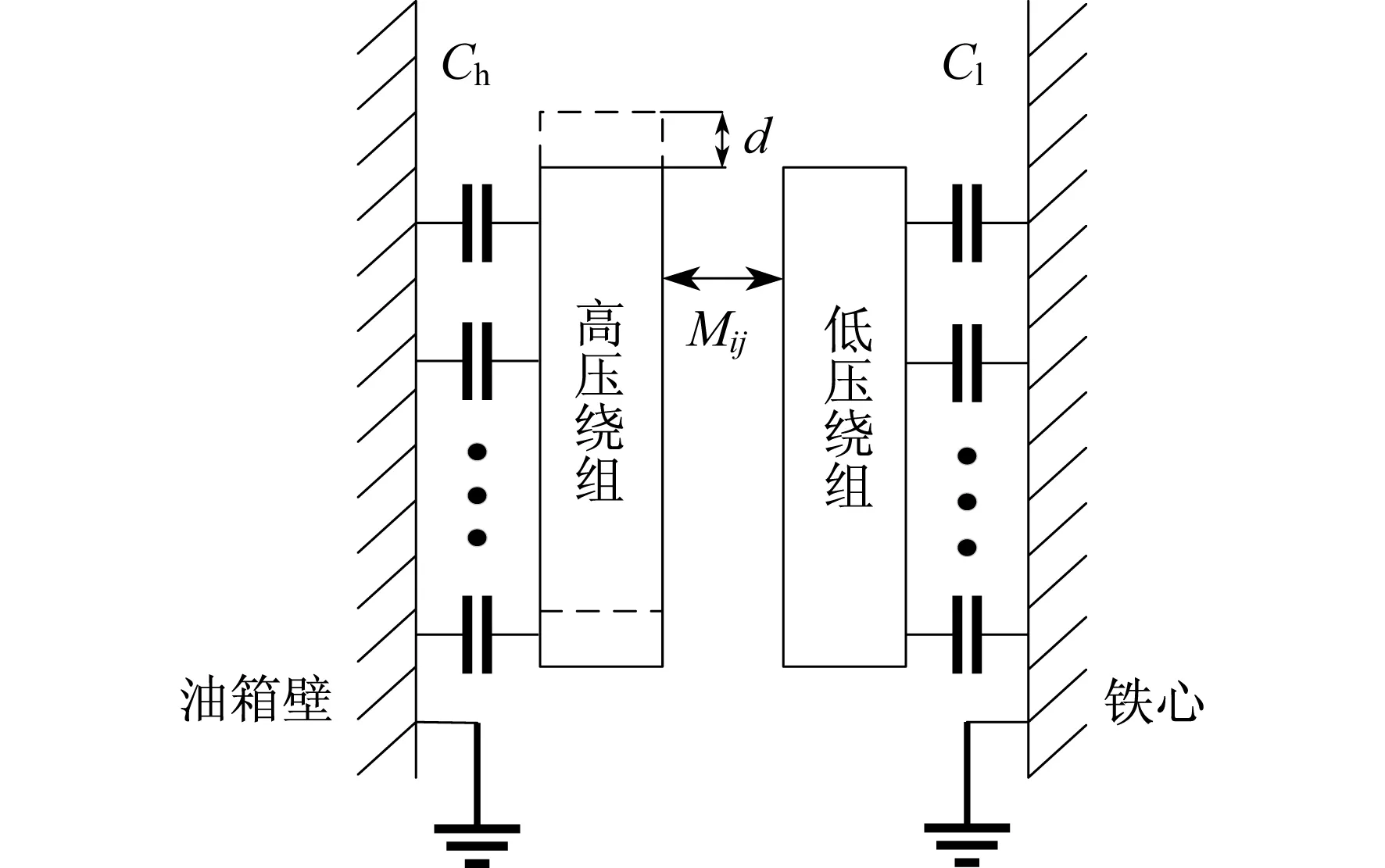
图3 高压绕组的轴向位移
3 结 语
本文主要分析了双绕组电力变压器集总参数模型,构建了串联阻抗支路矩阵和并联导纳支路矩阵,再基于基尔霍夫电流和电压定律来获取支路电流与节点电压之间的关系;同时分析了变压器绕组径向变形和轴向位移故障时的主要影响参数,以期为后续系统研究变压器绕组故障提供相关的理论基础。
