基于三角函数神经网络的电动汽车充电电流谐波分析方法
2019-01-07,,,,,
, , , , ,
(1.杭州市电力设计院有限公司, 浙江 310009; 2.上海电力学院, 上海 200090)
随着全球能源的逐渐枯竭、大气污染的不断加剧以及气温上升带来的危害加重,越来越多的人意识到节能减排是社会发展的方向。因此,电动汽车应运而生,并迅速得以广泛应用[1]。电动汽车作为电力负荷,其充电行为具有间歇性和随机性。在电动汽车充电过程中,由于充电器本身包含各种非线性特性的电力电子元件,会向电力系统注入谐波,当谐波超过一定范围,将会给电网带来谐波污染,从而对电网的稳定性产生影响,同时也将缩短电池的寿命,因此对电动汽车充电过程中的谐波进行分析和检测具有重要意义[2-4]。
为了减轻谐波污染,对谐波成分进行准确分析和检测是十分必要的,有利于将补偿技术应用于电流波形校正,提升电能质量,因此准确计算电流谐波幅值、相位等关键参数成为解决电力系统谐波污染的关键[5-7]。近年来,电动汽车电流谐波测量领域有了很大的进步,其中最常用的方法是快速傅里叶变换(Fast Furier Transform,FFT)。其优点是算法简单、应用灵活,而且适用领域较广泛;但是,因其釆样时间较长且变换时运算复杂,导致其测量时间较长,谐波分析的实时性较差。更重要的是,采样同步性会引起频谱泄漏效应和栅栏效应,进而导致谐波电流幅值、相位和频率等测量数据的估计存在误差[8-10]。近几年,人工神经网络以其鲁棒性好、精确度高、自学习性强等优点获得了广泛的应用。在电流谐波检测中,人工神经网络被用以提高检测的实时性和精确度,其中应用最多的主要是前馈自适应人工神经网络和自适应线性人工神经网络。但人工神经网络也存在一些局限性,如学习时间长、构造函数无法统一、需要庞大的样本数量等[11-14]。
为了实现电动汽车充电电流谐波分量的快速、准确检测,本文提出了一种新型的基于三角函数神经网络的谐波分析方法。利用该算法可以快速获得电流基波和各次谐波的幅值和相位,且三角函数神经网络算法满足收敛定理,鲁棒性较强。基于MATLAB的仿真结果证明,三角函数神经网络谐波分析方法可以快速、精确地估计电流谐波分量及相关参数,在电流谐波的实时检测中具有实用价值。
1 三角函数神经网络电流谐波检测
电动汽车的充电电流可以用幅值和相位表示为各个谐波分量之和,即
ω0t+φj)
(1)
式中:i(t)——电动汽车的充电电流;
idc(t)——电动汽车充电电流的直流分量;
N——电动汽车充电流谐波次数;
Aj——第j次谐波的幅值;
ω0——基波分量的角频率;
φj——第j次谐波的相位。
(2)
式中:wj——电流谐波参数。

1.1 构造三角函数神经网络
构造基于三角函数的神经网络,其结构如图1所示。输入层为n对训练数据集{x,y},x,y∈R1×n矩阵。其中x=(x(1),x(2),…,x(i),…,x(n)),y=(y(1),y(2),…,y(i),…,y(n)),x(i)=t(i)是第i个采样点对应的时间;y(i)是第i个采样点对应的电流瞬时值。
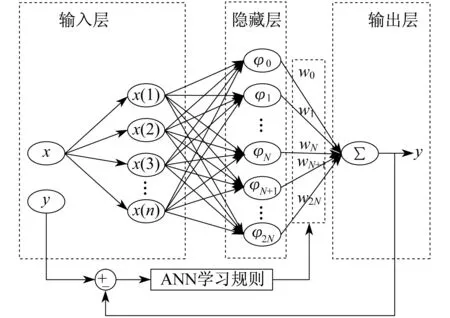
图1 三角函数神经网络结构示意
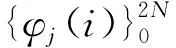
(3)
式中:φj(i)——第i个采样点对应于第j个隐藏神经元的激活函数。

φj(i)
(4)

wj——电流谐波参数,也是隐藏层和输出层之间的权重。
1.2 利用性能函数和负梯度下降法更新权重
设计学习规则性能函数为
(5)
基于负梯度下降法,设计三角函数神经网络的权重迭代公式为
w(k+1)=w(k)-ηPT(Pw(k)-y)
(6)
其中,
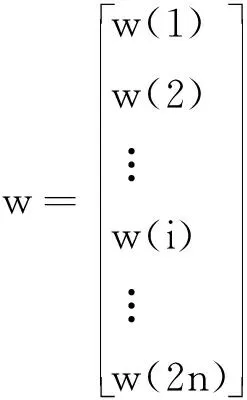
(7)
式中:k——迭代次数,k=1,2,3,…,iter,max(iter,max为最大迭代次数);
w(k)——第k次迭代对应的权重;
η——学习速率。
根据η的特性,若使η>0且足够小,可以通过迭代使三角函数神经网络的权重收敛于最优权重,其特性服从以下定理。

证明根据式(5)和式(6)可得
e(w(k+1))=
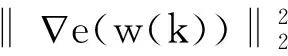


当0<η<η*=(2/λmax)(PTP)时,有

则有
e(w(k+1))≤e(w(k))+

因此可得
e(w(k+1))≤e(w(k))
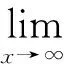
通过求解神经网络的权向量,可计算出直流分量以及第j次谐波的幅值和相角
(8)
式中:Adc——直流分量的幅值。
2 仿真与分析
2.1 方法流程
基于三角函数神经网络的谐波分析方法的流程图如图2所示。将计算估计得到的神经网络的输出电流与输入电流作比较,当不满足目标误差,即e(w)达不到期望设定值eobj时,用负梯度迭代法更新权重,实现对实际电流的准确、快速的估计。
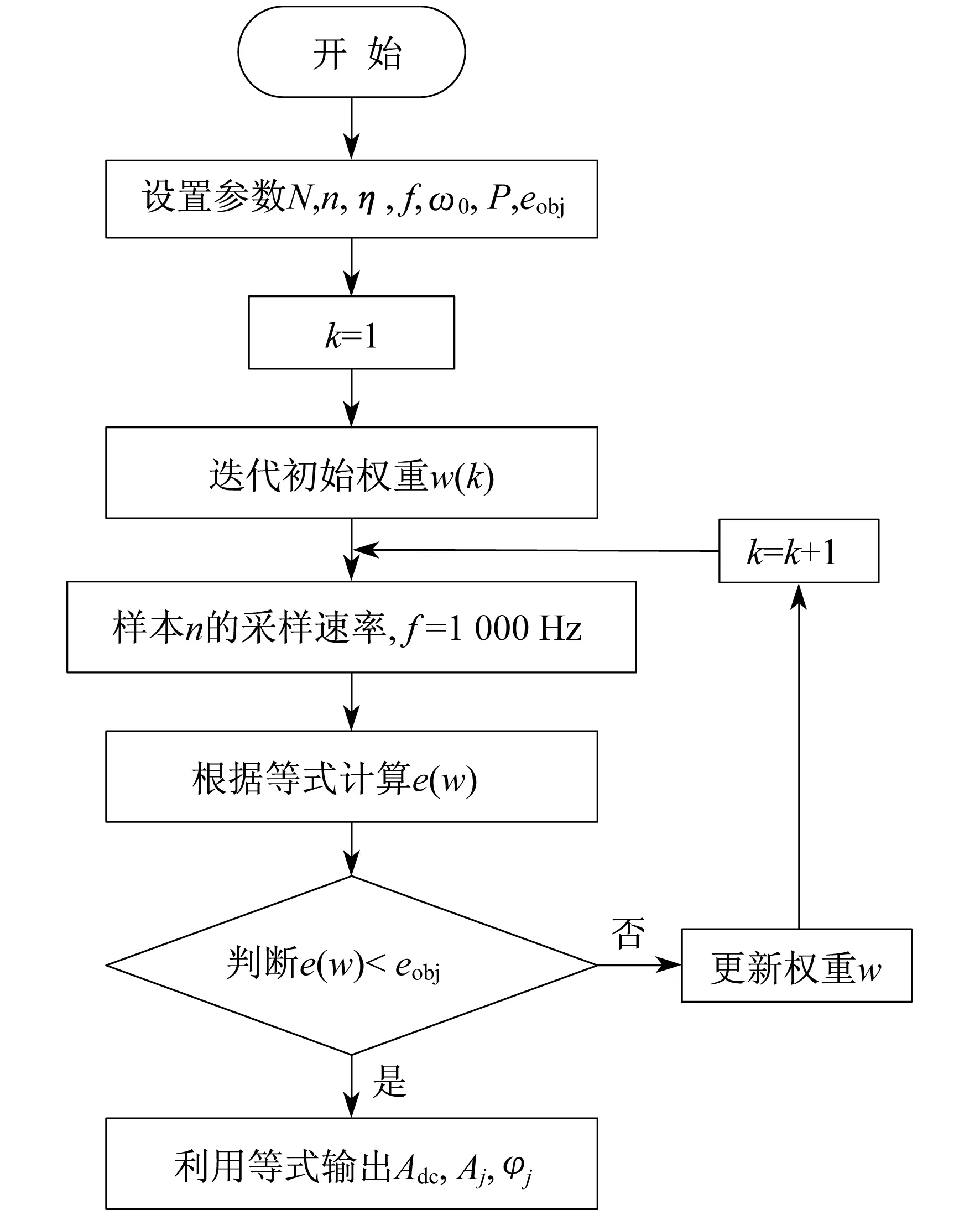
图2 基于三角函数神经网络的谐波分析方法的流程示意
2.2 仿真分析
为了验证三角函数神经网络谐波分析方法的正确性和有效性,通过MATLAB/Simulink对含有谐波的电流信号进行了仿真研究。电动汽车充电电流信号的表达式与式(2)相同。
其中,ω0设为100π rad/s,其他各次谐波的角频率为基波角频率的整数倍,谐波最高次数N=9,每次迭代的采样频率f=1 000 Hz,共采样10个点(即n=10)。仿真中所使用的电流信号基波和各次谐波的幅值及相位如表1和表2所示。
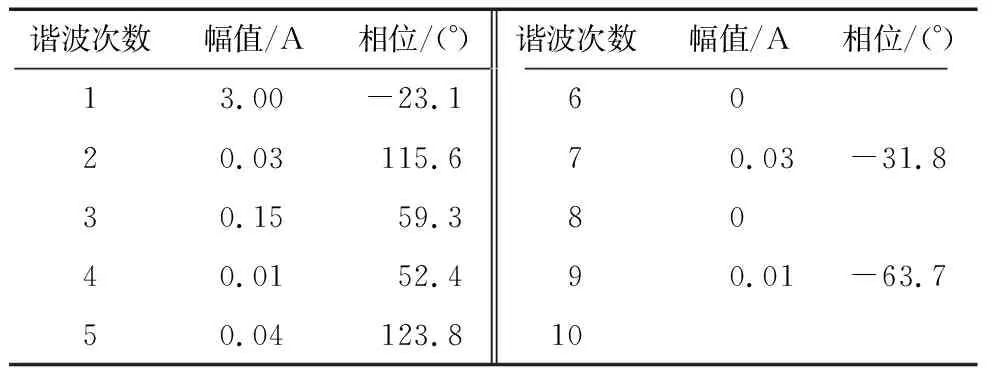
表1 慢充时电流信号的各个谐波分量
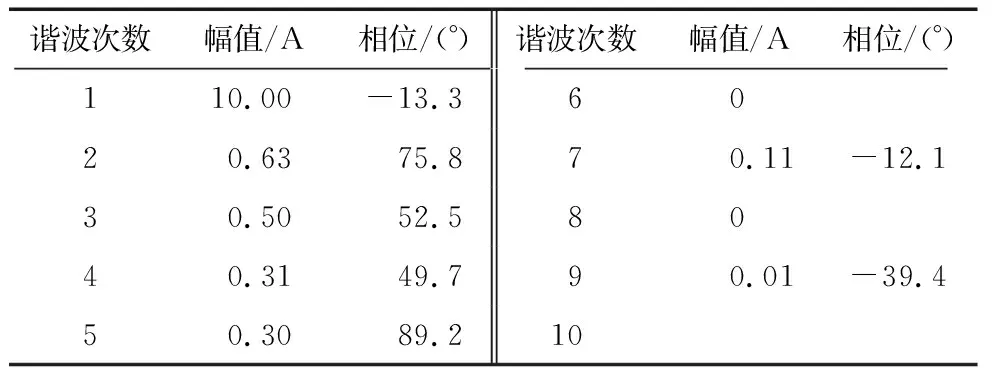
表2 快充时电流信号的各个谐波分量
仿真时,将额定工频50 Hz及采样值输入三角函数神经网络进行训练,即可快速获得基波和各次谐波的谐波频率、幅值及其相位,目标误差eobj设为0.001。
学习速率对本文算法的收敛性有较大影响,学习速率的大小决定了算法收敛的快慢。较大的学习速率能加快神经网络的学习,但可能引发系统震荡或发散,较小的学习速率可保证算法的收敛,但计算时间比较长[15-17]。通过仿真得出不同学习速率下神经网络的收敛性和迭代次数,如表3所示。取最优学习速率为0.01。

表3 不同学习速率下的神经网络收敛性和迭代次数
2.3 结果对比
为了证明三角函数神经网络分析谐波的优越性,将其与FFT进行对比,仿真结果如图3至图6所示。由图3至图6可以看出,三角函数神经网络和FFT均能够跟踪基波和其他各个分量的幅值和相角,但FFT需要至少一个周期(0.02 s)才能得出计算结果,而三角函数神经网络只需要半个周期(0.01 s)就可以跟踪到相应的幅值和相角,将有助于电力系统的实时检测和快速保护。与FFT控制下的波形相比,三角函数神经网络能够快速地跟踪到实际电流信号的各个分量。

图3 慢充条件下两种方法的基波分量与3次谐波幅值波形
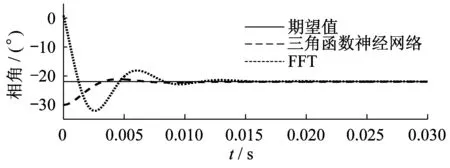
图4 慢充条件下基波分量相角波形
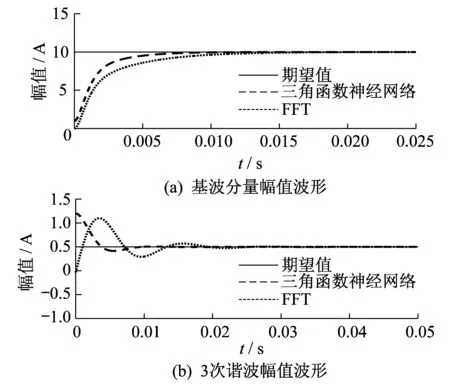
图5 快充条件下两种方法的基波分量与3次谐波幅值波形
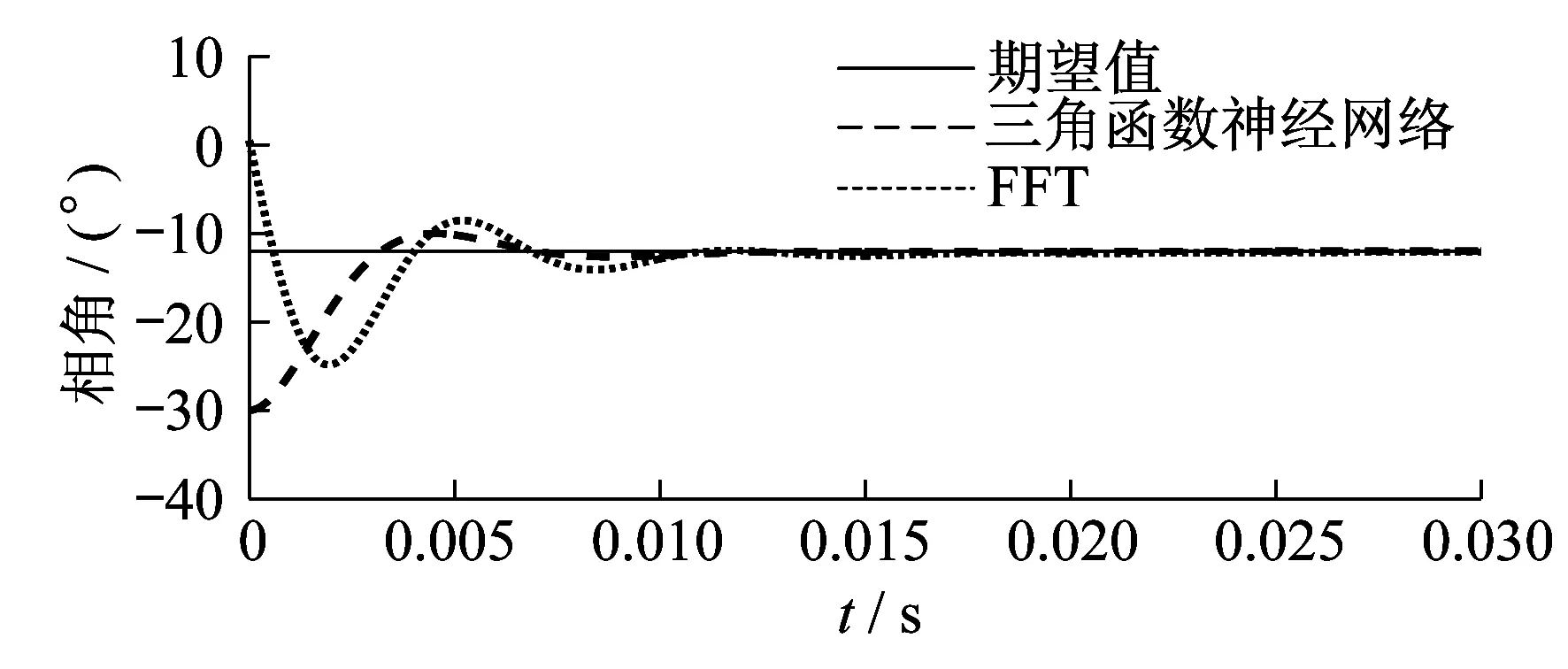
图6 快充条件下基波分量相角波形
3 结 语
针对电动汽车充电过程中造成电力系统产生谐波的问题,通过建立三角函数神经网络模型,设计了基于三角函数神经网络的电流谐波分析方法。在迭代过程中通过对权值的修正,提高测量的准确性。通过仿真分析,将所提出的方法与传统方法进行对比,验证了本方法能够更快速、精确地估计系统谐波分量的相关参数,为实现电动汽车充电过程中谐波抑制方法的设计提供了借鉴。
