基于非合作博弈的布谷鸟搜索算法在微电网多目标优化中的应用

, , ,

(1国网上海市电力公司市南供电公司,上海 200233; 2.上海电力学院, 上海 200090;3.国网上海市电力公司松江供电公司, 上海 200122)

随着全球对能源与环境问题的日益关注,太阳能、风能等可再生能源在各领域得到了广泛的应用,而微电网作为能够充分促进分布式电源与可再生能源大规模接入的小型发配电系统,也得到了迅速的发展[1-2]。从一系列支持分布式能源并网的文件和政策的下发可以看出,高比例可再生能源并网将成为电力系统的必然发展趋势和未来重要特征[3]。但随着更高比例可再生能源的接入,其出力的间隙性与不确定性往往造成自身及微电网功率波动,从而影响微电网的稳定安全运行。

目前国内外已有许多关于高比例可再生能源并网优化的研究。文献[4]提出了在高可再生能源渗透率下的微电网经济调度模型,将模型细分为日前计划和实时调度两层,兼顾了可再生能源利用率及其功率波动特性;文献[5]在分布式能源与负荷双重不确定性叠加的背景下,提出了一种新的灵活性平衡机制,实现了源-网-荷-储复杂场景下的综合灵活性优化;文献[6]建立了以网损最小与分布式能源出力效率最高为目标的多目标优化模型,提出了一种基于小生境进化的多目标免疫算法,并分析了不同权重系数对优化结果的影响。

博弈论作为一门具有多个决策主体的优化方法论,已在电力系统规划、电力市场、调度、控制等方面得到了大量应用[7]。在微电网多目标优化问题中的各个目标一般存在竞争关系,每个目标均企图使自身收益最大[8]。将博弈论应用于确定多目标的权重系数中,可以克服已有多目标优化加权系数法受限于决策主观性的不足,通过Nash均衡找到同时满足多个目标的最优权重系数。

本文以一个包含了光伏(Photovoltaic,PV)、风力发电机(Wind Turbine,WT)、蓄电池(Storage Battery,SB)及用户负荷的并网型微电网为对象,为了实现可再生能源利用率最大化、并网冲击最小化,分别将微电网购电成本和联络线功率波动系数作为指标,用以反映微电网的经济效益与稳定安全。基于二人零和博弈模型优选出最佳权重系数,并采用布谷鸟搜索算法(Cuckoo Search,CS)求解微电网多目标优化问题。最后,对该风-光-储混合发电系统(Hybrid Power System,HPS)进行了仿真,并与传统的多目标优化方法进行了对比,以验证该模型和算法的有效性与可行性。

1 微电网系统优化模型

1.1 微电网建模

1.1.1 光伏电池模型

光伏电池的功率特性可表示为[9-10]

(1)

式中:PSTC——标准测试条件下(入射强度为1 kW/m2,外界温度为298.15 K)的最大测试功率;

GAC——光照强度,取1 kW/m2;

GSTC——标准测试条件下的光照强度;

k——功率温度系数,取-0.47%/K;

Tc——电池板的工作温度;

Tr——参考温度,一般为25 ℃。

1.1.2 风机出力模型

风机每时段的发电量是由风机转轴处每时段的平均风速及风机的出力特性决定的,其输出功率可根据风机生产厂家提供的网侧输出功率曲线经过多项式拟合得到,具体公式[11-12]为

(2)

式中:Pr——风机的额定功率;

vci,vr,vco——风机的切入风速、额定风速和切出风速。

各系数可通过风机输出功率曲线拟合得到。

1.1.3 蓄电池模型

蓄电池可用于平抑负荷波动、削峰填谷,并网时可实现定联络线功率控制;与风机、光伏等可再生能源发电相配合可以来稳定系统的输出功率,加强可再生能源发电的可调度性[13]。蓄电池在t时刻的剩余电量与蓄电池在t-1时刻的剩余电量、t-1时刻到t时刻的充放电量以及每小时的电量衰减量有关。

蓄电池充放电时,t时刻的剩余电量(State of Charge,SOC)分别为

(3)

(4)

式中:VSOC(t)——t时刻蓄电池的剩余电量;

PSB(t)——t时刻蓄电池的充放电功率;

ηC,ηD——充放电效率;

DB——蓄电池每小时的自放电比例;

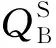
1.2 目标函数的建立

1.2.1 经济效益函数

针对上述微电网,其可再生能源的并网比例可用微电网向大电网购买的电费成本来衡量。购电成本以实时电价与联络线上的缺额功率的乘积来描述,其公式为

Δt

(5)

PMar,t=PPV,t+PWT,t-PLoad,t-PSB,t

(6)

式中:PCost,t——购电实时电价;

PMar,t——微电网与电网联络线上的功率缺额;

Δt——调度周期;

PPV,t——光伏向微电网提供的出力;

PWT,t——风机向微电网提供的出力;

PLoad,t——t时刻的负荷功率;

PSB,t——蓄电池在t时刻的储能功率。

1.2.2 联络线随机功率波动函数

对于可再生能源大量并网时产生的冲击对电网稳定性造成的影响,可以用联络线在t时刻流过的功率与t-1时刻流过功率的差值绝对值来表示[14-15],其公式为

(7)

1.2.3 综合考虑经济效益和并网稳定性

将经济效益函数F1与并网稳定性函数F2进行加权,可把F1和F2多目标问题转化为F3单目标问题进行求解。即

minF3=λF1+(1-λ)F2

(8)

式中:λ——权重系数,0≤λ≤1。

1.2.4 约束条件

(1) 有功功率平衡约束为

+PSB,t+PGrid,t-PLoad,t=0

t=1,2,3,…,Ti

(9)

式中:Pi,t——t时刻第i种发电功率;

PGrid,t——t时刻微电网与外电网的交换功率;

Ti——仿真优化总时长。

(2) 蓄电池一次充放电量约束为

t=1,2,3,…,Ti

(10)

式中:VSOC,t——蓄电池第t时刻的SOC值;

PBatt,t——t时刻蓄电池的功率;

这个人喝下热水之后，觉得自己可以站起来了，甚至还可以像想象中一个快死的人那样走路了。他每走一两分钟，就不得不停下来休息一会。他的步子软弱无力，很不稳，就像跟在他后面的那只狼一样又软又不稳；这天晚上，等到黑夜笼罩了光辉的大海的时候，他知道他和大海之间的距离只缩短了不到四哩。

BCAP——蓄电池总容量。

(3) 蓄电池运行约束为

PSB,mi≤PSB(t)≤PSB,ma

(11)

-Sinv,SB≤PSB(t)≤Sinv,SB

(12)

式中:PSB,mi——蓄电池最小有功功率;

PSB,ma——蓄电池最大有功功率;

Sinv,SB——逆变器容量。

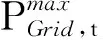
(13)

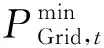
2 基于二人零和博弈的多目标线性加权法

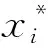
其模型所述如下。

(1) 参与者可分为参与者1和参与者2(虚拟参与者)。

(2) 策略集为

fi∈{f1,f2,f3,…,fn}

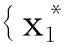
(14)

(3) 支付为fi(xi)和-fi(xi)。

由于原问题中的各目标函数量纲并不一致,故需对其进行相应的归一化处理,即

,j=1,2,3,…,n

(15)

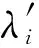
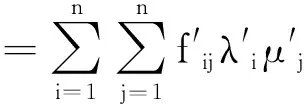
(16)

若F′表示某种成本,则参与者1的目标是使F′最小化,而参与者2的目标是使F′最大化,据此可写出二人零和博弈模型为

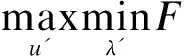
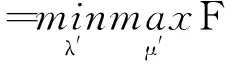
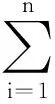
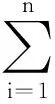
(17)

博弈问题的求解等价于求解两个线性规划问题

s.t.ri≥0

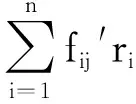
s.t.sj≥0

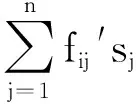
(18)

求解上述两个优化问题后所得的最优支付为

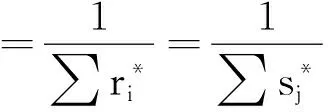
(19)

博弈问题的混合策略Nash均衡为

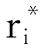
(20)

故可得到原优化问题各目标的权重系数为

,2,3,…,n

(21)

应用上述所得权重系数便可将原问题转化为单目标优化问题进行求解,即

λifi

(22)

3 布谷鸟搜索算法及其优化算法流程

3.1 布谷鸟搜索算法概述

布谷鸟搜索算法(CS)是由剑桥大学学者YANG X S和DEB S于2009年提出的一种新颖的启发式智能优化算法[16]。该算法根据大自然中布谷鸟寻找到鸟巢后放置鸟蛋的行为,以及鸟类的Levy飞行行为,结合大量的随机和标准测试进行对比分析。实验结果表明,相较其他的智能优化算法,该算法获得的优化效果更显著。因该算法具备结构简单、参数较少,且无需大量匹配参数的优点,已逐渐应用于工程设计优化问题中。

布谷鸟搜索算法主要基于以下3个理想化的规则[17]:

(1) 假设每只布谷鸟每一次只能孵下一只蛋,并随机寻找鸟巢将其放置于其中;

(2) 鸟巢位置即代表解,将最好的鸟巢位置保留到下一代,这就相当于是遗传算法中的精英主义;

(3) 设鸟蛋被发现概率为Ra(Ra∈[0,1]),Ra越大表示该鸟蛋存在更大机率被筑巢鸟丢弃,或是直接寻找新的一处构筑新的鸟巢位置。

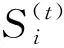
∂⊕Levy(λ)

i=1,2,3,…,n

(23)

式中:∂——步长比例因子;

⊕——点对点乘积;

Levy(λ)——符合参数为λ的Levy分布,即Levy～μ=t-λ(1<λ≤3)。

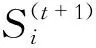
3.2 在微电网多目标优化中的布谷鸟优化算法流程

(1) 根据上述微电网模型,确定微电网中各个出力单元的取值范围,迭代次数为N,初始概率参数Ra取0.25。

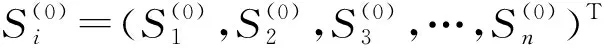
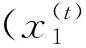
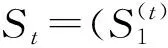
(5) 通过比较测试后的测试值,选出St中最优的鸟巢位置,并判断是否满足最大的迭代次数。若满足则中止循环;反之,则返回第3步,进入循环体进行迭代更新,直到满足条件。

(6) 输出步骤5中得出的最优解对微电网进行各出力单元的优化。

其优化算法流程[17]如图1所示。

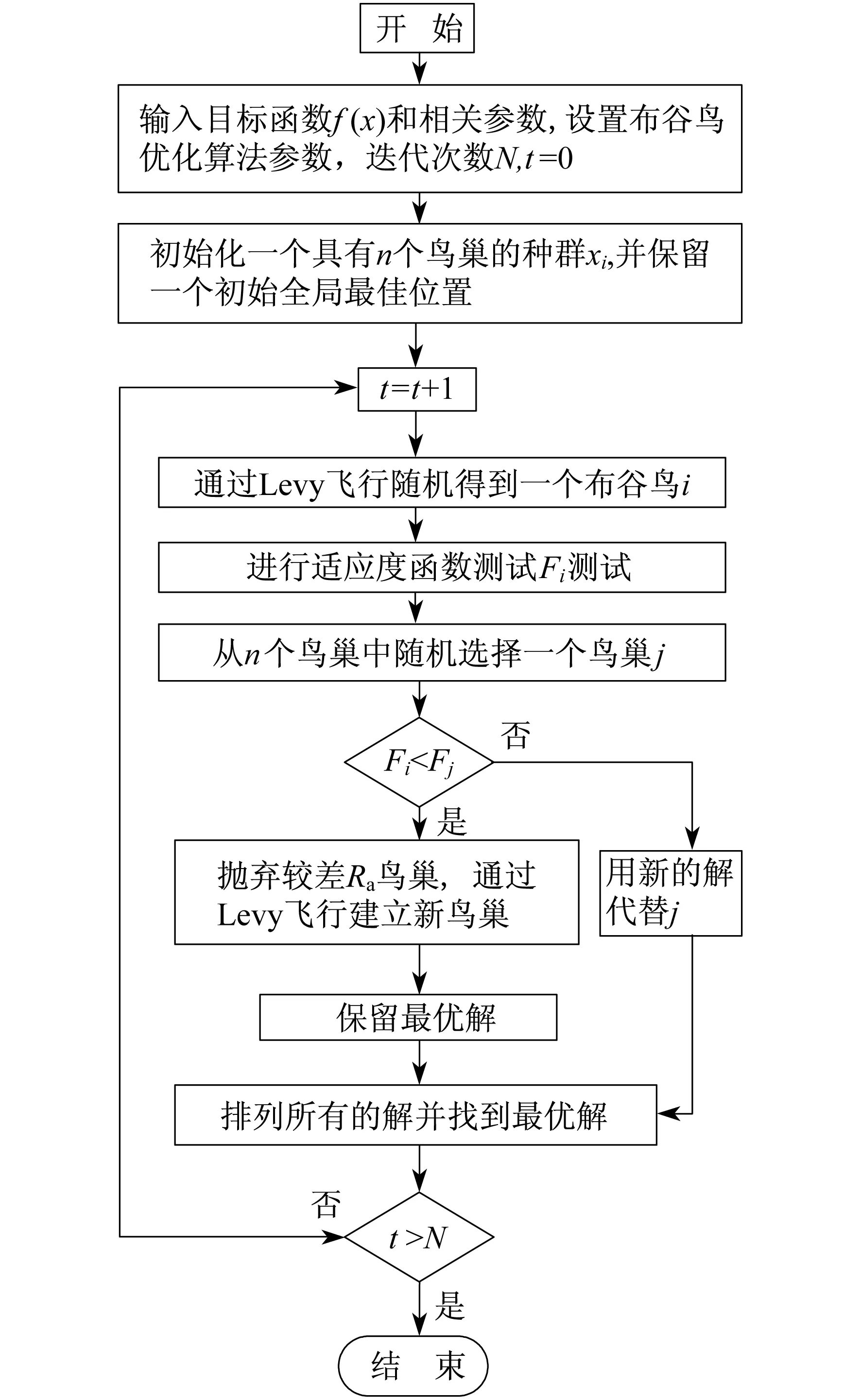
图1 优化算法流程示意

4 算例分析

本文算例采用的是风-光-储微电网结构,由光伏列阵、风力发电机、储能系统(蓄电池)以及用户负荷组成。该微电网为并网型微电网,与外网交互时,优先利用微源满足微电网内负荷需求。若发生功率缺额,且自身无法靠蓄电池补给,则可以从外网吸收功率。微电网每小时调度一次,峰平谷分时电价如表1所示。

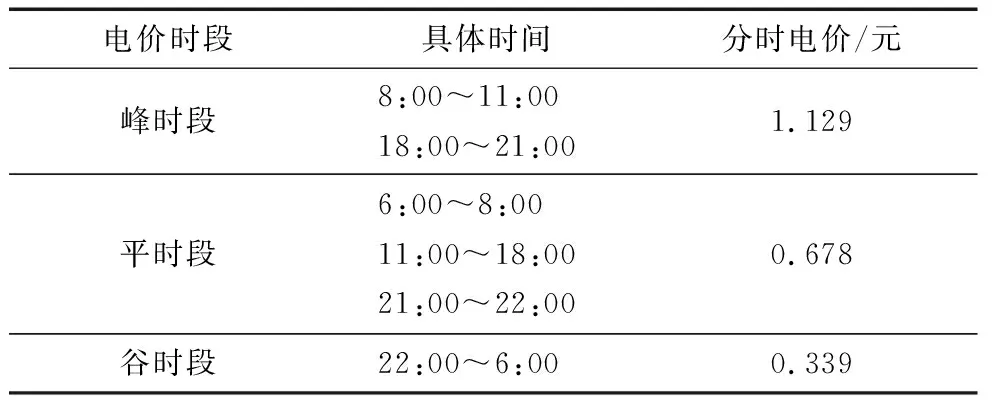
表1 峰平谷分时电价表

设蓄电池额定容量为50 kWh,初始电量设置为60%额定容量,充放电效率ηC和ηD设为1,SOC最大容量为100%额定容量,最小容量为30%额定容量;逆变器容量最小取-20 kW,最大容量取20 kW。根据光伏阵列和风机模型,计算得出光伏和风机的最大允许出力以及预测负荷曲线如图2所示。

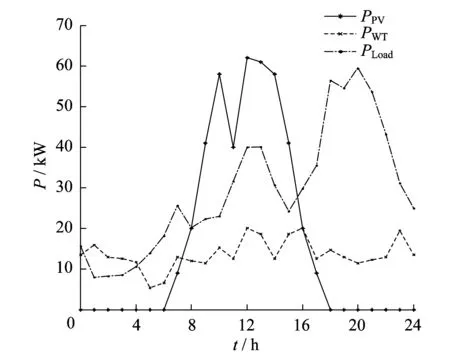
图2 光伏发电和风力发电的出力及负荷曲线

首先,以微电网购电成本与联络线功率波动为主要优化目标,得到最佳的优化结果。分别记作xC和xP,并计算每种优化方式对应的购电成本f1和波动系数f2;然后,引入两个虚拟参与者,将其策略分别设为f1和f2及xC和xP,形成二人零和博弈模型。其支付矩阵如表2所示。

表2 微电网优化问题零和博弈的支付矩阵

根据式(16)所建立的二人零和博弈问题,可求得混合策略Nash均衡解λ1=0.666 7,λ2=0.333 3。

由此,便可确定各个目标的权重系数,将多目标优化问题转为单目标优化,将布谷鸟搜索算法应用于微电网的优化调度中,得到的优化结果如图3所示。图3中,PGrid1是主要考虑优化波动系数后的联络线功率;PGrid2是以最小化购电成本为主要优化对象后的联络线功率;PGrid3是基于上述二人零和博弈模型下,同时考虑了购电成本与波动系数后的优化结果。

表3给出了在不同优化目标下的优化结果。表3中,单目标优化是指仅以最小化购电成本或功率波动为目标的粒子群算法后的优化结果;多目标优化是指先将某一个目标作为主要的优化对象,再将另一个优化目标作为约束条件添加到原问题的约束集中得到的计算结果;二人零和博弈是指利用本文所述的二人零和博弈模型,确定各目标的权重系数,再应用布谷鸟搜索算法得到的优化结果。

由表3可知,本文提出的博弈方法能够较好地兼顾经济性与稳定性,计算结果明显优于传统优化算法。

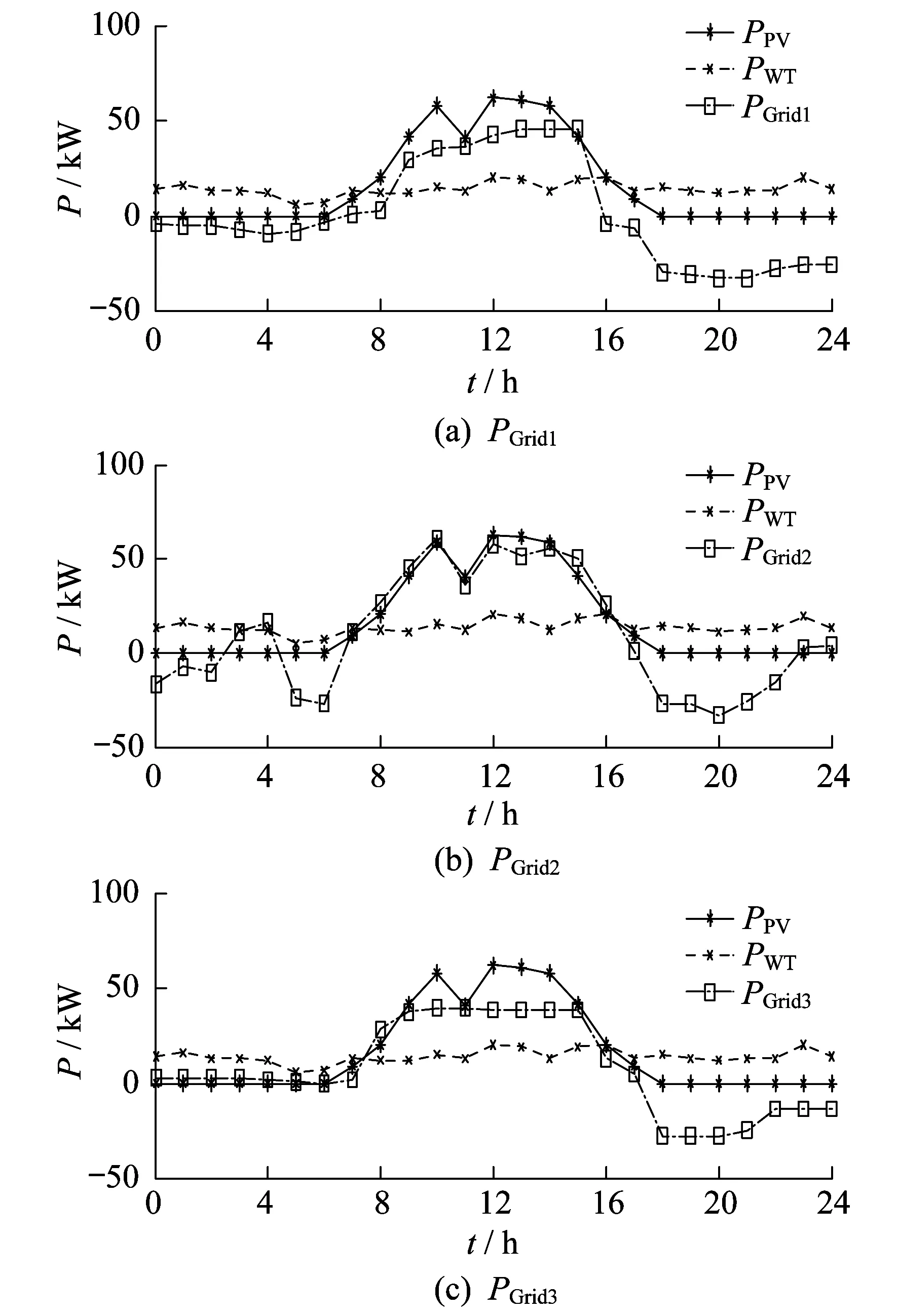
图3 不同优化方法下HPS功率输出波动

优化方法目标购电成本/元联络线波动/kW费用增加/%波动增加/% 单目标优化购电成本154.295 0 联络线波动 103.7 0 多目标优化购电成本178.400169.515.62263.452联络线波动194.618129.026.13424.397 二人零和博弈 170.264117.510.35012.374

5 结 语

本文建立了以可再生能源利用率最大化和联络线功率波动最小化为目标的微电网多目标优化模型。在此基础上,采用了二人零和博弈模型来寻找到该微电网多目标优化模型的最佳权重系数,再应用布谷鸟搜索算法对该模型进行了优化。结果表明,本文所提方法可以使两者通过双方各自效益最大化进行博弈,最终得出Nash稳定策略下的最佳权重系数,使HPS整体利益最大化。相比传统人工主观定义权重系数的方法,该方法能够实现更平滑的电力输出,同时提高了可再生能源的利用率。