不同约束滑道形状对多边形效应的影响
2019-01-07王国晋梁艳书钱兰珠
王国晋,梁艳书,洪 林,钱兰珠
(1.天津商业大学 机械工程学院,天津 300134;2.天津福臻工业装备有限公司,天津 300350)
0 前言
链传动的多边形效应会对链条的工作性能产生非常严重的影响,特别是对大节距的输送链[1-2]。文献[3]对滑道约束型输送链做出了静态和动态理论的分析,建立了常规输送链数学模型,并计算出所需的动态参数。文献[4]提出了三种降低套筒滚子链传动多边形效应的常用方法,但本文中并不能够用到。本文是采用改变滑道形状的方法来比较多边形效应的强弱的,通过对不同形状的滑道进行分析,得出所需的参数,从而明确所提方案的优缺点。通过对比分析,验证所构建的不同形状的滑道约束型输送链是否能够减小其多边形效应。
1 滑道约束型模型
常规链条模型如图1所示。为了简化后续计算,使右侧半个圆周上正好可以放置三个链节[5]。从右侧主动轮开始按顺时针顺序给销轴取统一编号P1~P18,把P17作为自由销轴,每两个链节之间的长度p=150,两侧链轮的半径r=150,左右两链轮中心距为D=900,初始时P17的位置在预定滑道上。

图1 常规输送链模型
在现实使用中链条会出现受空间约束等特殊情况,所以提出两种解决方案,将上下边直线型滑道设计成向外凸出的圆弧型和向内凹进的圆弧型两种,称其为凸弧型输送链和凹弧形输送链两种,如图2和图3所示。其中凸弧型左右链轮的中心距为886,上下滑道均为半径2000的圆弧;凹弧型左右链轮的中心距为874,上下滑道均为半径900的圆弧。初始时图2和图3中的P17均偏离了预定滑道。α1表示销轴P1与主动链轮圆心连线和轴正半轴之间的夹角,同样的αn表示销轴Pn与靠近链轮连线和轴正半轴之间的夹角。假设右侧轮的角速度大小ω=π。因为三种模型中除了自由销轴外,其余销轴均已被滑道所约束,所以微小的中心距变化所产生的误差忽略不计。并且为了方便计算,本文仅分析在顺时针转动下的情况。

图2 凸弧型输送链模型
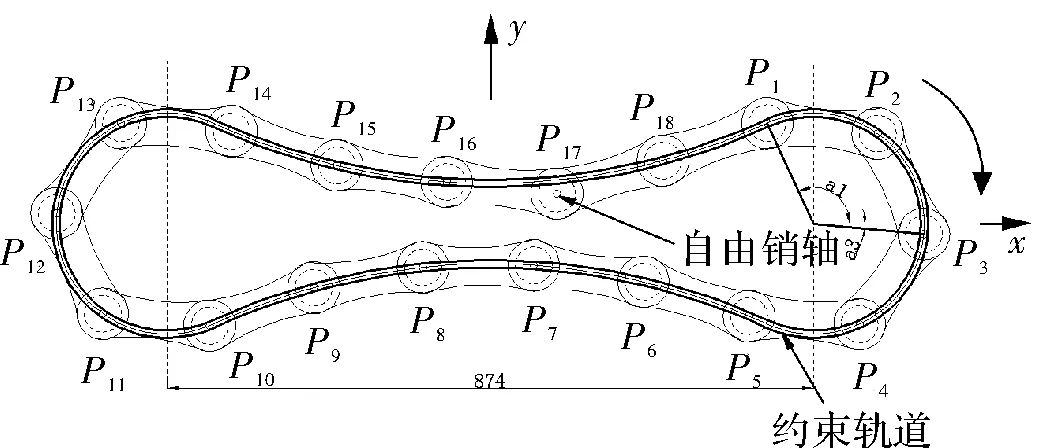
图3 凹弧型输送链模型
2 多边形效应的表示方法
根据文献[3]中的方法,使用Matlab软件算出P17运行一周所经过的位置坐标,然后采用描点法获得在静态下的轨迹。在运动过程中,销轴在左右两个过渡区域会存在较大的多边形效应,销轴在速度上会有较大的差别。但是,因为除了P17外全都被滑道约束,所以由于不同的速度所产生的位移差就会全部表现在P17上。
为了表示多边形效应的强弱,把左右过渡位置的销轴在一个周期内的位移变化表示出来,位移变化越大则表明P17的振动越剧烈,即多边形效应越强烈。以滑道的上半部分为研究对象,常规输送链模型的运动分析图如图4所示。
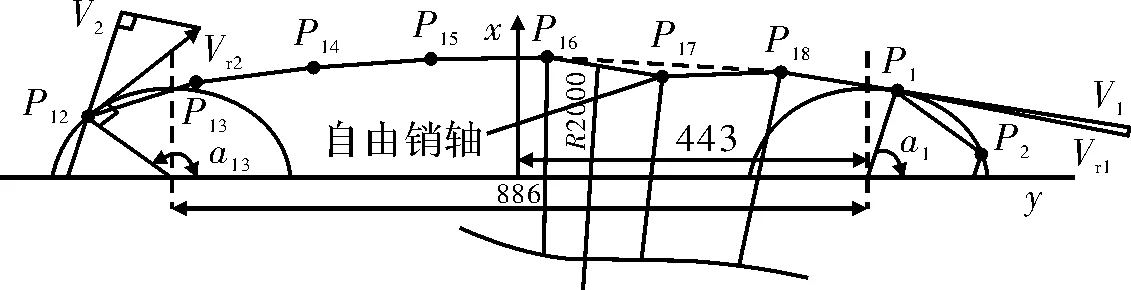
图4 常规输送链运动分析

图5 凸弧型输送链运动分析
图4中v1、v2为P1、P13的有效速度;vr1、vr2为P1、P13的真实速度;s1、s2为P1、P13的位移。可推导出v1和s1的计算公式为
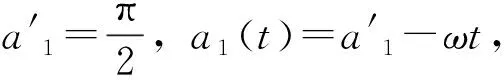

在一个周期内,和均有可能处于过渡区域,所以
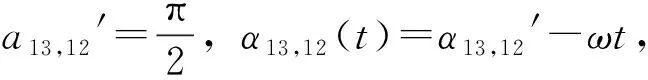

位移差为

(1)

(2)
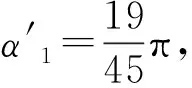
凹弧型输送链运动分析如图6所示,位移差为

(3)

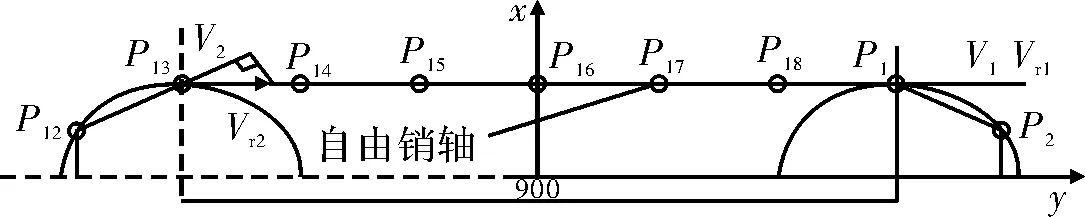
图6 凹弧型输送链运动分析
3 多边形效应仿真
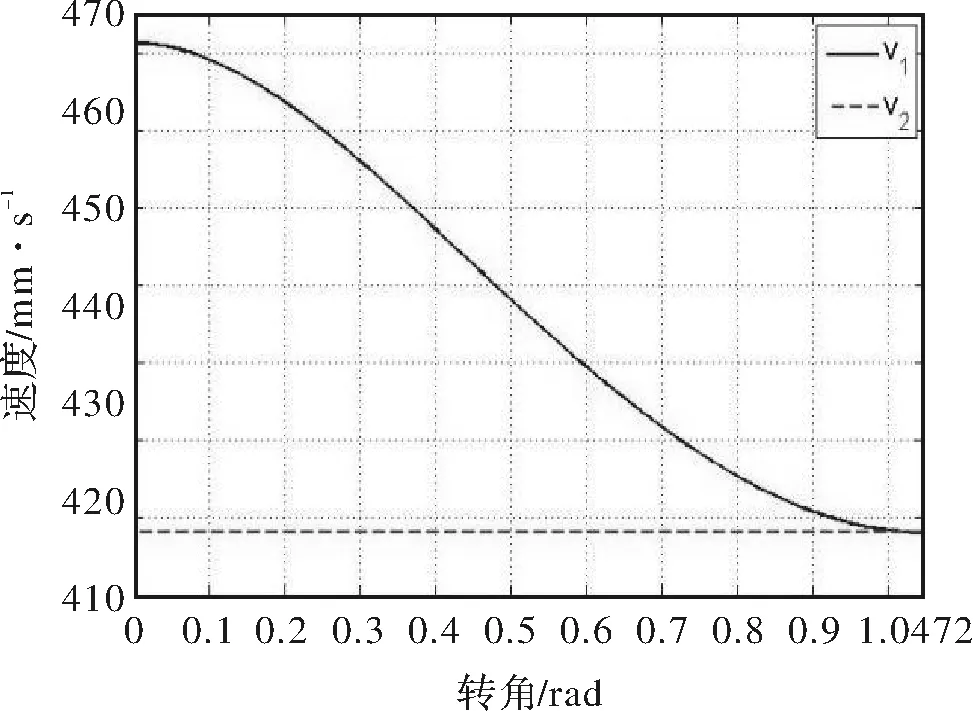
图7 常规输送链过渡区销轴速度
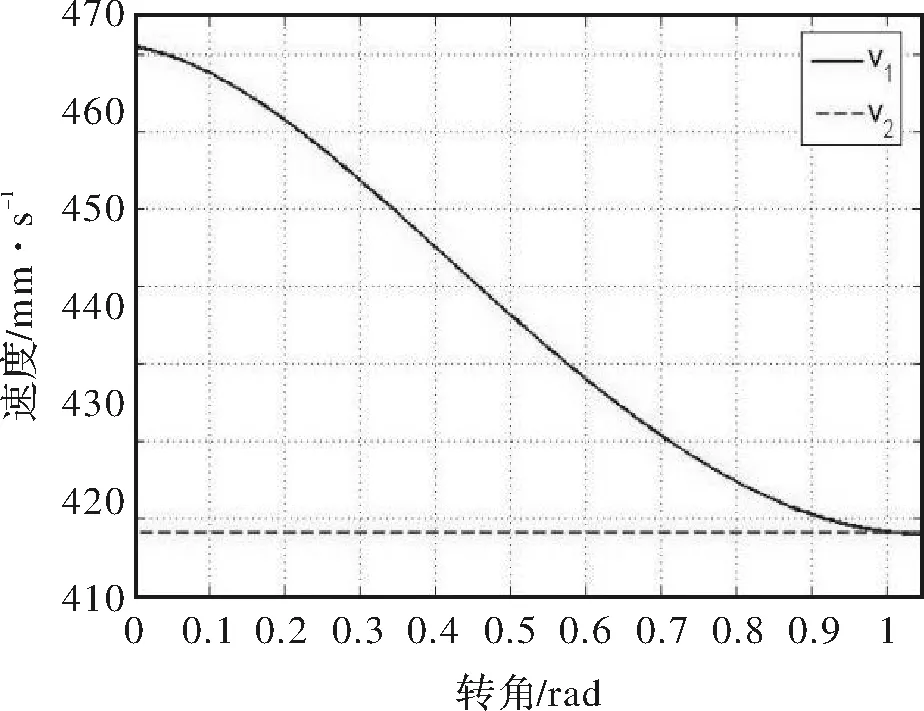
图8 凸弧型输送链过渡区销轴速度
式(1)、 (2)和(3)是对两个销轴的速度积分作差而得到的位移差。由积分原理可知,将一个周期内时间段分割成有限的区间,用每个微小时间段内的某一时刻的速度来代替该时间段内的速度,然后将各段位移相加即得总位移,同一模型中两不同销轴的总位移作差即得总位移差。分割的区间越小,所得结果越准确。使用Matlab软件得到的3种模型的总位移差如图10所示。
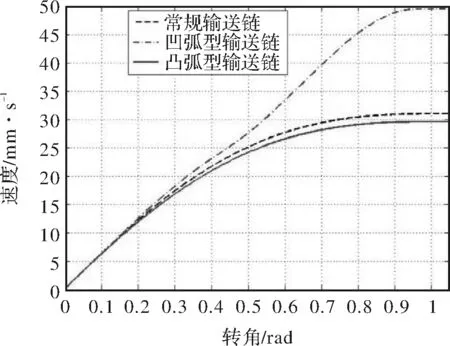
图10 输送链过渡区销轴的总位移差
4 结论
对不同模型进行仿真分析比较多边形效应的强弱,结果表明,相对于常规输送链来说,凸弧形输送链两侧销轴的总位移差变小,可以减少链传动的多边形效应;凹弧形输送链的总位移差变大很多,会使多边形效应愈发明显。在设计滑道约束型模型时,可以将直线滑道通过圆弧型滑道代替,圆弧滑道应使用凸弧型滑道来适当减小链传动中的多边形效应。
