油管动力钳双联齿轮轴的模态分析

胡宝军，陈 东，周井玲，许雪松

(1.江苏如通石油机械股份有限公司，江苏 南通 226400；2.南通大学 机械工程学院，江苏 南通 226000)

0 前言

油田的修钻井作业中最为关键的环节就是管柱的上卸扣作业，国内外的所有产品中动力大钳和铁钻工是使用最为广泛的工具。动力大钳按照使用用途可以分为：钻杆动力钳、套管动力钳和油管动力钳[1-2]。美国WEATHERFORD公司在2005年开发了一种闭口动力钳，并在2005年获得了近海技术会议最优机械装置的荣誉，这款动力钳最大的特点就是主钳和背钳是一体式的，上管柱与下管柱可以实现迅速对中，有利于动力钳的平稳运行[3]。

XQ140/20油管动力钳是一种在油田上快速上卸螺纹的一种开口式动力钳，适用于直径范围在Φ42～Φ140 mm范围内的油管，与同类型的其他液压动力钳相比，具有结构紧凑、操作方便、性能可靠、使用寿命长等优点。

XQ140/20油管动力钳主钳系统是由齿轮传动带动的，而齿轮在传递较大的载荷时，轮齿的啮合表面始终处于接触状态，导致轮齿间的接触、分开、再接触的反复冲击，对主钳系统动态特性产生了不良的影响。这些将会导致动力钳的振动，影响动力钳使用的可靠性与安全性[4-6]。

1 油管动力钳双联齿轮轴固有频率的理论计算

解决振动问题的方法，不外乎是理论分析方法与实验研究方法，二者是相辅相成的。而理论方法首先要做的就是依据研究的对象建立对应的物理参数模型，即以质量、阻尼、刚度为参数的关于位移的振动微分方程，然后求得特征值和特征向量，进而得到模态参数模型即系统的模态频率、模态向量、模态阻尼等[7]。

以主钳传动系统的双联齿轮轴为研究对象，轴上有双联齿轮、轴承、轴承密封圈、衬套，双联齿轮组件及双联齿轮轴，分别如图1和图2所示。

图1 双联齿轮组件

图2 双联齿轮轴

对双联齿轮轴进行简化处理，将其简化成等截面的轴，轴的当量直径为

(1)

式中，L为双联齿轮轴的长度；ln为阶梯轴每段的长度；dn为阶梯轴每段的直径大小；d为当量直径，计算后求得当量直径d=29 mm。

简化之后的物理参数模型如图3所示。

图3 双联齿轮轴的物理参数模型

1.1 瑞利商法

首先通过瑞利商法估算系统的基频。多自由度系统的运动微分方程一般为

(2)

式中，M为系统的质量矩阵；C为系统的阻尼矩阵；K为系统的刚度矩阵；F(t)为外部激励列阵。

由于所求的是双联齿轮轴的自由模态，所以振动微分方程中阻尼矩阵C为0，外部激励列阵F(t)也为0，简化之后的振动微分方程为

(3)

采用瑞利商法计算双联齿轮轴的基频。根据瑞利商法可以得到

(4)

式中，R(ω)是一个标量，任取一向量w并将向量k和向量m带入式(4)中，最终求得双联齿轮轴的基频为 3 978.21 Hz。

1.2 柔度系数法

通过瑞利商法对双联齿轮轴的基频进行了理论计算，但是瑞利商法所求得的特征值永远不会低于第一特征值，而第一特征值也就是瑞利商能取的极小值。所以使用柔度系数法对双联齿轮轴进行固有频率的理论计算，并把计算处的结果和瑞利商法求出的基频进行比较。

依然使用所建立的物理参数模型和振动微分方程。将微分方程(3)两边同时除以[k]ω2，将其转化为关于固有频率的振动微分方程。转化之后的微分方程为

(5)

式中，fij为柔度系数，可以通过当量直径d将柔度系数解出

(6)

求解式(5)可以求出双联齿轮轴前3阶的圆频率，通过式(6)可以知道圆频率和固有频率之间的关系，进而求出双联齿轮轴前3阶的固有频率，表1为双联齿轮轴的前3阶固有频率。

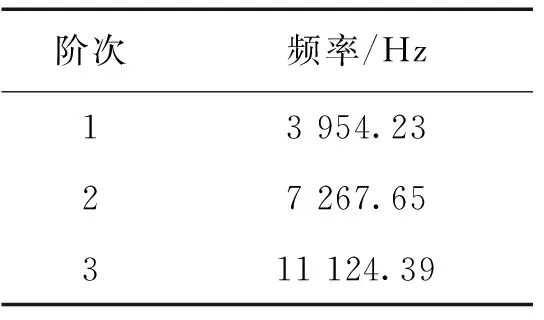
表1 双联齿轮轴前三阶固有频率

通过理论计算发现：双联齿轮轴前面3阶的固有频率均远远大于液压马达的旋转频率16 Hz, 所以不会产生共振。

通过将柔度系数法所求的基频与瑞利商法所求的基频进行对比，二者相差了2.3%，且瑞利商法所求的基频略大于柔度系数法所求的基频。

2 双联齿轮轴的有限元模态分析

随着计算机技术的飞速发展和有限元软件的日趋成熟，采用有限元分析法已经可以对双联齿轮轴进行模态分析[8]。

对双联齿轮轴进行有限元模态分析，首先就是要建立双联齿轮轴的有限元模型。所以先在ANSYS Workbench中建立双联齿轮轴的三维模型，并对其进行适当的简化处理，除去双联齿轮轴上的圆角、倒角等特征，然后将双联齿轮轴的材料属性设置为：密度ρ等于7 800 kg/m3,弹性模量E等于2×105MPa,泊松比μ等于0.3。网格大小设置为2 mm,然后对双联齿轮轴进行自由网格的划分，如图3所示。

图4 双联齿轮轴的网格划分示意图

对双联齿轮轴进行自由模态的分析，为了方便找出规律，取双联齿轮轴前13阶频率和振型进行分析，表2列出了其前13阶的模态结果。

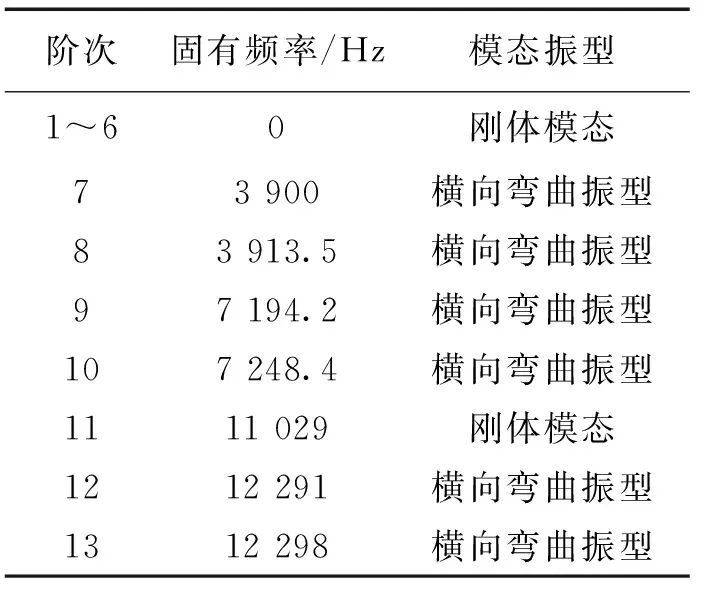
表2 双联齿轮轴前13阶模态结果

根据有限元模态分析的结果得出双联齿轮轴的各阶固有频率和模态振型，1～6阶自由模态均是刚体模态，而第11阶双联齿轮轴产生刚体转动，也没发生变形。因为双联齿轮轴为轴对称模型，所以除了刚体模态以外的模态都是两两相等，从图5和图6可以证实这一点。

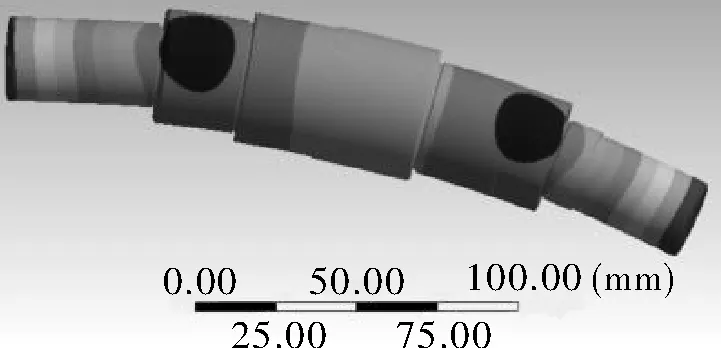
图5 双联齿轮轴第7阶振型

图6 双联齿轮轴第8阶振型

图7和图8分别显示了第9阶和第12阶的模态振型。通过图片可以看出双联齿轮轴的各段均有明显的弯曲振动，且随着固有频率的增加，双联齿轮轴的振动也越来越大。除了刚体模态，双联齿轮轴最小的固有频率为3 900 Hz，远远大于液压马达的频率16 Hz，所以双联齿轮轴完全避开了共振频率。

图7 双联齿轮轴第9阶振型

图8 双联齿轮轴第12阶振型

3 双联齿轮轴的实验模态分析

实验模态分析作为研究模态的重要手段和方法。通过人为的激励输入时结构产生振动，然后运用数字信号处理技术获得频响函数、脉冲响应函数等，再运用参数识别方法，求得系统的模态参数[9]。通过B&K测试得到了双联齿轮轴的实验模态，并将之与理论计算和有限元模态分析结果进行对比。三种求解方法的比较见表3。

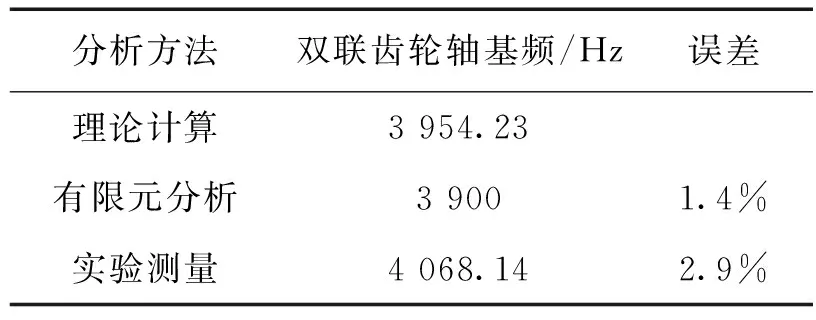
表3 双联齿轮轴的理论、有限元、实验模态分析对比

理论计算求出双联齿轮轴的基频为3 954.23 Hz；有限元分析求出双联齿轮轴基频为3 900 Hz,与理论计算的误差仅为1.4%，而通过B%K声学与振动测试仪器测量双联齿轮轴的固有频率为4 068.14 Hz，与理论计算的误差为2.9%，验证了有限元分析对于双联齿轮轴模态分析的正确性。通过有限元分析得出双联齿轮轴的多阶模态频率和模态振型。

4 结论

(1)通过瑞利商法和柔度系数法两种理论方法计算双联齿轮轴的基频，两种方法所求基频相差2.3%，由于瑞利商法是近似求解，所以取双联齿轮轴的基频为3 954.23 Hz。

(2)使用ANSYS Workbench有限元分析软件对双联齿轮进行有限元模态分析，与理论计算相差为1.4%，使用B&K仪器对双联齿轮轴进行模态分析，与理论计算相差为2.9%，三者相近，验证了有限元分析的正确性，也验证了实验模态分析的准确性，为油管动力钳的动力学优化分析做了标定，提供了理论依据。