非穿透型齿根裂纹扩展及啮合特性分析
2019-01-07刘杰孙玉凤王成烨
刘杰,孙玉凤,王成烨
(沈阳工业大学 机械工程学院,辽宁 沈阳市 110870)
0 前言
齿轮系统作为传递运动和动力的关键部件,其性能的好坏将直接影响整个机械系统的精度与稳定性[1]。在齿轮传动中,啮合刚度的时变特性是齿轮传动系统一种主要的动态激励源,将会引起系统的动态响应。郭辉等[2]利用有限元法模拟齿根裂纹扩展过程。Pandya[3]等基于线弹性断裂力学的二维弹性体,使用二维有限元模拟直齿圆柱齿根的裂纹扩展。万志国等[4-5]分析了齿根裂纹扩展及不同深度的齿根裂纹对时变啮合刚度的影响。Hui Ma等[6-7]利用多种方法计算裂纹对啮合刚度的影响并与有限元法相比较,从而验证了有限元法的精确性。Chang等[8]利用有限元法与解析法相结合的方法,提出了啮合力、齿轮参数对齿轮啮合刚度的影响。唐进元等[9]利用有限元方法,分析了不同载荷下齿轮的啮合刚度。陈锐博等[10]通过有限元法,分别讨论了在不同负载以及发生轴向偏载的情况下齿轮啮合刚度的变化规律。常乐浩等[11]利用有限元法和弹性接触理论相结合的方法,分析了齿轮的啮合刚度。王旭等[12]利用材料力学的方法把齿轮简化为变截面的悬臂梁,分析了裂纹对齿轮啮合刚度的影响。崔玲丽等[13]利用有限元法与能量法计算了含裂纹齿轮的啮合刚度,证实了有限元法的有效性。国内外许多著名学者都对裂纹齿轮进行了研究,但是对于非穿透型裂纹齿轮的裂纹扩展和啮合刚度的研究较少。
本文通过ANSYS有限元软件,在建立齿轮系统有限元模型的基础上,利用有限元法模拟了三维非穿透型齿根裂纹在齿宽方向的扩展过程,并分析了齿宽方向不同穿透程度的齿根裂纹以及齿廓方向裂纹尾部不同高度,对齿轮啮合刚度和等效应力、总位移的影响。
1 齿根裂纹扩展
1.1 裂纹尖端附近的应力和位移场
根据断裂力学理论[14],裂纹可分为三种类型,即Ⅰ型裂纹(张开型裂纹)、Ⅱ型裂纹(滑开型裂纹)、Ⅲ型裂纹(撕开型裂纹)。齿根裂纹同时存在Ⅰ型和Ⅱ型,即齿根裂纹为复合型裂纹,裂纹扩展示意图如图1所示。
对于Ⅰ型裂纹,裂纹尖端应力场为
(1)
对于Ⅱ型裂纹,裂纹尖端应力场为
(2)
式中,KⅠ、KⅡ为Ⅰ型、Ⅱ型裂纹应力强度因子;r、θ为裂纹尖端附近点的极坐标。
将式(1)和(2)转化为极坐标方程,并运用叠加原理得到裂纹尖端附近的极应力表达式
(3)
裂纹沿着应变能释放率达到最大的方向扩展,即
(4)
(5)
由式(4)、(5)可求得开裂角θ=θ0,即裂纹扩展角计算公式为
(6)
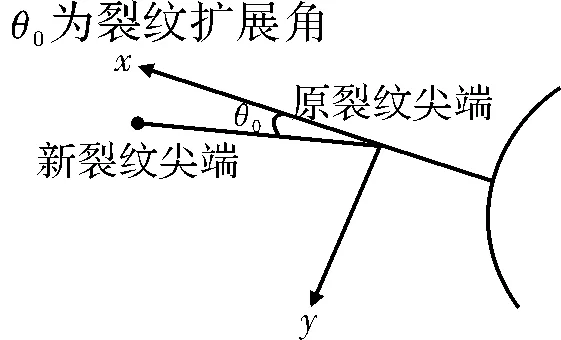
图1 裂纹扩展示意图
1.2 齿根裂纹扩展模拟
在健康齿轮模型的基础上建立三维齿根裂纹有限元模型,齿轮参数见表1。初始裂纹长度为5 mm,当齿根裂纹扩展到15 mm时的有限元模型如图2a所示。根据断裂力学理论解得应力强度因子KⅠ、KⅡ,同时求得裂纹扩展角确定裂纹扩展路径由A扩展到B,如图2b所示。经计算,应力强度因子历程曲线如图3所示。

表1 齿轮副基本参数

图2 齿根裂纹模型
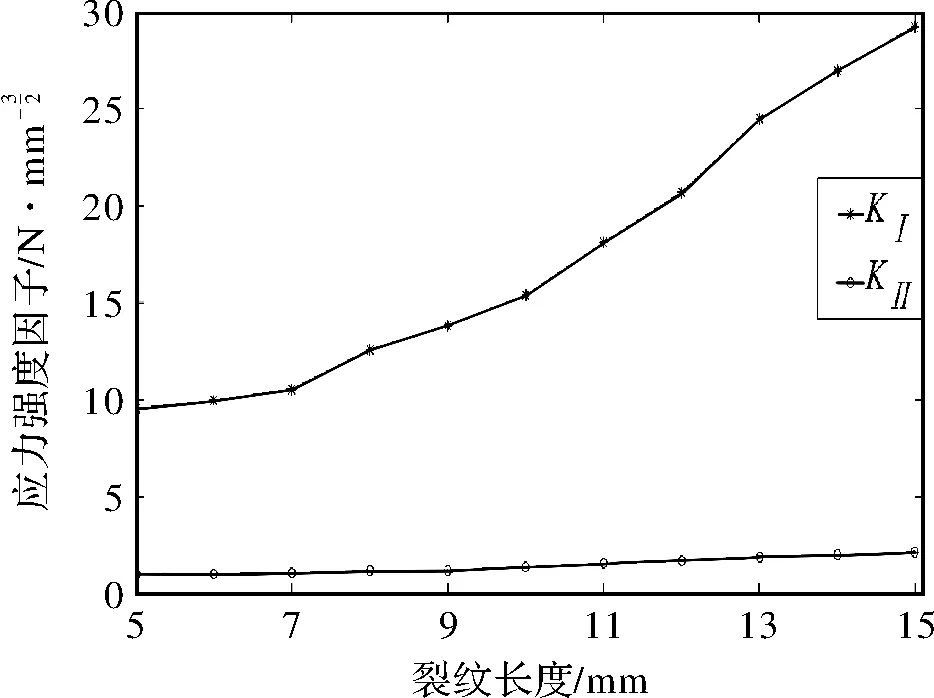
图3 应力强度因子随裂纹长度的变化曲线
由图3可知,非穿透型裂纹由5 mm扩展到15 mm的过程中,随着裂纹长度的增加应力强度因子逐步增加。KⅠ的增加幅度更加显著,且KⅠ远远大于KⅡ,由此可表明,齿轮的断裂主要受Ⅰ型裂纹的影响。
2 齿轮啮合刚度分析
2.1 有限元法分析齿轮啮合刚度
建立三维四对齿轮体有限元模型,对主动轮内孔边界所有节点施加切向力F来模拟转矩,健康齿轮加载模型如图4所示。其中,切向力的大小由公式(7)来确定。

图4 齿轮副加载模型
切向力F的表达式为
(7)
式中,T为输入扭矩;ri为主动轮内孔半径;n为小动轮内孔边界节点数。
在健康齿轮模型建立的基础上,创建裂纹深度q=1 mm、裂纹扩展角β=45°,在齿宽方向和齿廓方向采用布尔运算建立不同穿透程度Lc和不同高度hi的齿根裂纹,如图5所示。由图5c可以看出,当hi=0 mm时,图5b中的裂纹类型就变成了图5a中的裂纹类型,图5a中的Lc即为图5c中的OB。
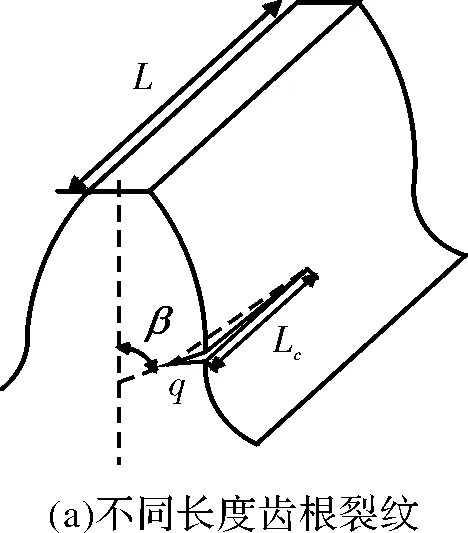
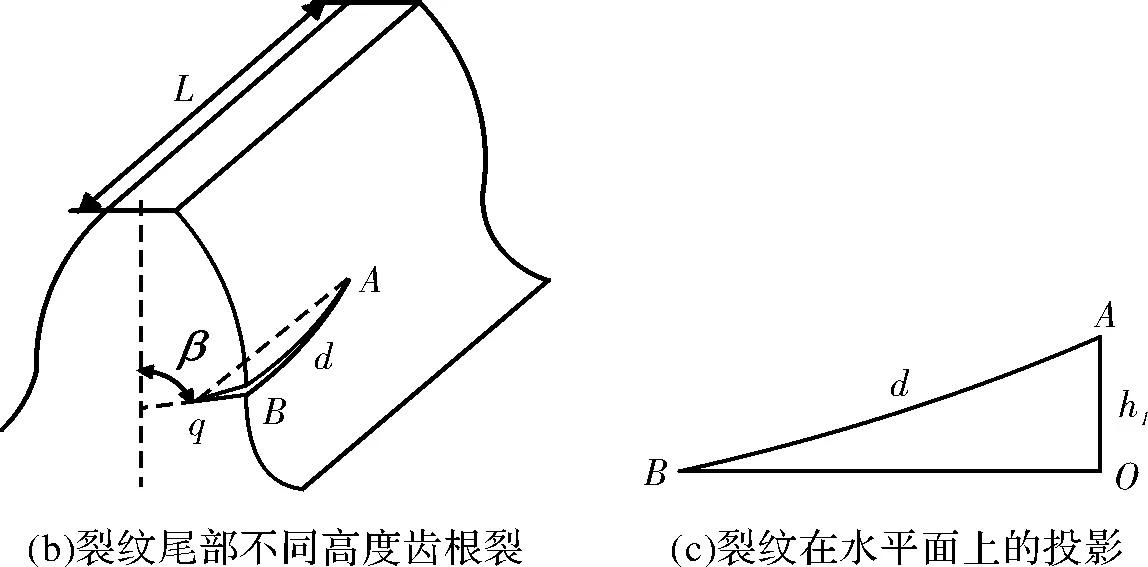
图5 齿根裂纹示意图
齿轮单双齿交替啮合产生的周期性变形是引起齿轮刚度激励的原因,轮齿变形的大小直接影响齿轮的啮合刚度。
啮合刚度公式
(8)
扭转啮合刚度公式
(9)
扭转啮合刚度与啮合刚度的关系为
(10)
因此齿轮啮合刚度公式
(11)
式中,T为齿轮转矩;Δθ为齿轮转角变形值;rb为基圆半径。
假设双齿啮合在零角度位置,在单双齿啮合区的内设置合理的步长,提取每一转角下的变形量,由啮合刚度计算原理求得啮合刚度,如图6所示。
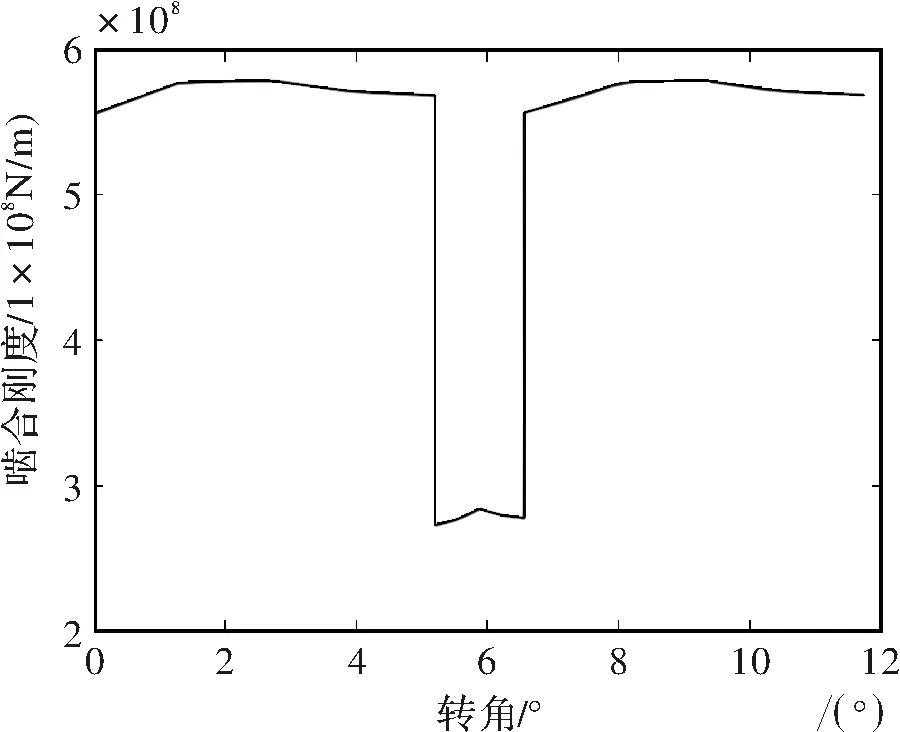
图6 健康齿轮啮合刚度
2.2 ISO验证健康齿轮啮合刚度
ISO6336-1∶2006中给出,单对齿啮合刚度的最大值为
(12)
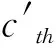
(13)
式中,q′为轮齿柔度的最小值,mm·μm/N
(14)
式中,Zn1为小齿轮当量齿数;Zn2为大齿轮当量齿数;系数参数如表2所示。

表2 系数参数
齿轮啮合刚度均值的计算公式为
cr=(0.75εa+0.25)c′
(15)
式中,εα为重合度。
由ISO标准可知,α=20°的齿轮副,当变位系数X1≥X2、-0.5≤X1+X2≤2时,单齿啮合刚度的最大值为[15]
k=0.8×103b/q′ N/mm
(16)
利用有限元法和ISO标准计算齿轮的单齿啮合刚度最大值、齿轮啮合刚度均值,两者相互比较,如表3所示,可得到有限元法与ISO标准值较为接近,由此证明了有限元法的有效性。

表3 啮合刚度计算误差比较
3 裂纹齿轮啮合刚度分析
3.1 不同穿透程度的裂纹齿轮的啮合刚度
不同穿透程度的裂纹齿轮,即为图5c中hi=0 mm,只改变OB的长度(即OB=Lc)。在健康齿轮模型的基础上,创建非穿透型齿根裂纹,来模拟实际工程中的齿轮裂纹情况,如图5a所示。其中深度q=1 mm,裂纹扩展角β=45°,齿宽方向裂纹穿透程度为25%、50%、75%、100%(即Lc=5 mm、10 mm、15 mm、20 mm)的裂纹。在通透型裂纹尖端处,采用四分之一节点位移法,将裂纹尖端附近单元边上的节点调到裂纹尖端节点位置,使得裂纹尖端处网格具有奇异性,如图7所示。
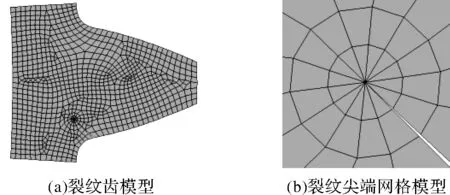
图7 裂纹齿轮网格模型
根据健康齿轮啮合刚度的分析方法,来分析裂纹深度q=1 mm,裂纹扩展角β=45°,齿宽方向不同穿透程度的齿根裂纹对齿轮啮合刚度的影响。提取主动轮扭转变形量,由啮合刚度计算原理计算出啮合刚度值,如图8所示。
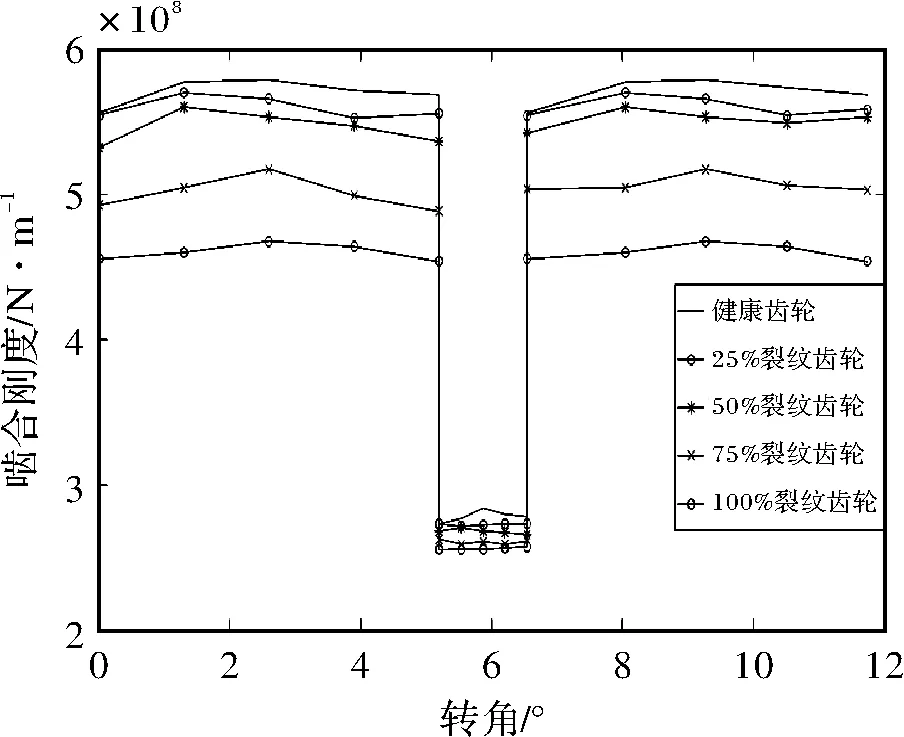
图8 不同穿透程度的裂纹齿轮啮合刚度
由图8可知,在裂纹齿参与啮合的两个啮合周期内啮合刚度都有所减小,并且后一啮合周期较前一啮合周期减小的幅度稍小。随着裂纹在齿宽方向穿透程度(Lc)的增加,啮合刚度的降低幅度随之增加。Lc从0增加到50%的时候,齿轮副啮合刚度的减小幅度稍小;当Lc从50%增加到75%、75%增加到100%时啮合刚度的减小幅度明显增大。
3.2 齿廓方向裂纹尾部不同高度的裂纹齿轮的啮合刚度
为了进一步分析非穿透型裂纹对齿轮副啮合刚度的影响,还考虑了齿廓方向裂纹尾部不同高度的裂纹齿轮,即为图5c中OB不变,只改变hi的高度。建立了深度q=1 mm,裂纹扩展角β=45°,齿宽方向裂纹穿透程度为50%裂纹齿轮(即Lc=10 mm),齿廓方向裂纹尾部的高hi设为从分度圆处投影到水平面(即图5c中的OB)平均分为三份(即hi=0 mm、0.65 mm、1.30 mm、1.95 mm)的裂纹齿轮,如图5b、图5c所示。
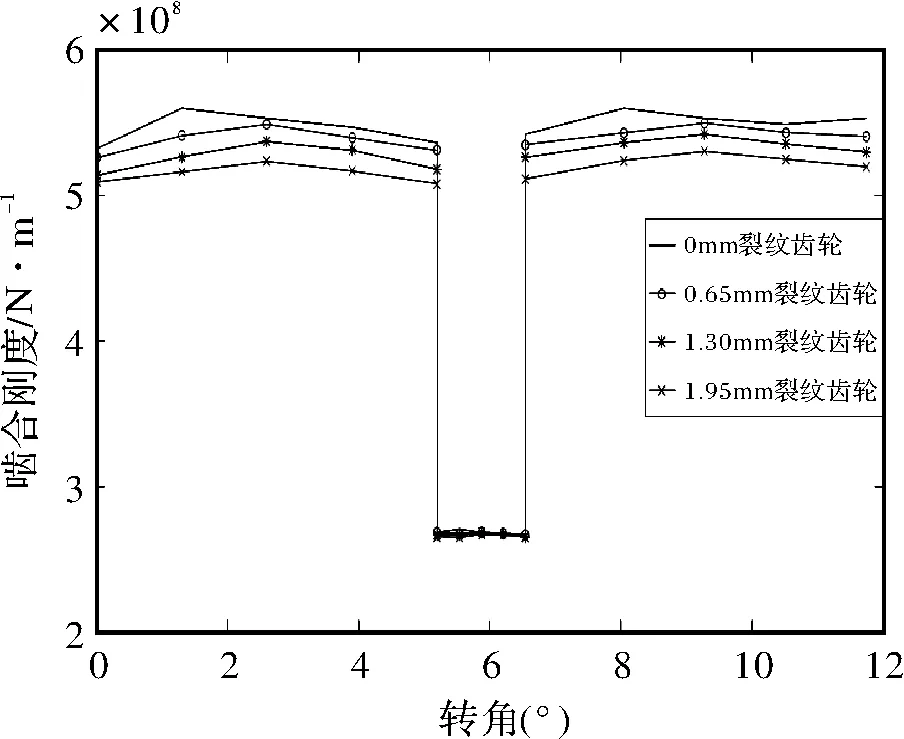
图9 裂纹尾部不同高度裂纹齿轮啮合刚度
由图9可知,当hi不断增大时,啮合刚度则随之逐渐减小。其中双齿啮合区的减小幅度要稍大些,单齿啮合区的减小幅度明显小于双齿啮合区的减小幅度。从齿宽方向50%的裂纹,齿廓方向hi为0 mm增加到1.95 mm时啮合刚度的减小幅度几乎相同。
4 不同裂纹类型对等效应力及位移的影响
为了分析不同裂纹类型对等效应力和总位移的影响,提取了主动轮上四条路径的等效应力和总位移,路径位置如图10所示。路径1为此时的啮合线、路径2在分度圆处、路径3靠近裂纹处、路径4最靠近齿根处,四条路径上的等效应力如图11所示,总位移如图12所示。
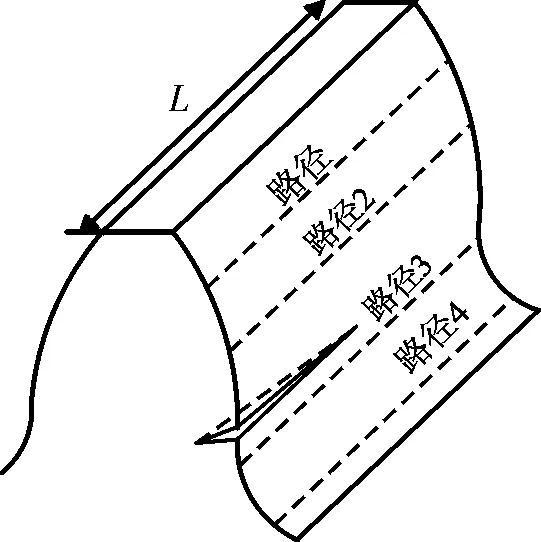
图10 主动轮上的路径位置示意图
对于健康齿轮,等效应力的分布沿齿宽不均匀,如图11所示。两齿边缘的等效应力与齿中间的应力不同,表明等效应力和应变状态分别出现在齿缘和中间部分。
对于穿透程度达到50%的裂纹齿轮,如图11b、图11c、图11d所示(即路径2、3、4中),在裂纹部分(即齿宽在0~10 mm处)的等效应力小于非穿透型裂纹健康部分的等效应力。然而,路径1上的50%裂纹齿轮的等效应力的变化趋势与健康齿轮的变化趋势相似,这是因为路径1为此时的啮合线。
通透型裂纹齿轮的等效应力分布类似于健康齿轮应力的分布。然而,等效压力的大小是不同的。当出现裂纹时,路径2、3、4下的等效应力急剧下降。以路径3为例,裂纹部分的等效应力约为0.095×109Pa,而健康齿轮对的应力约为1.27×109Pa如图11c所示。
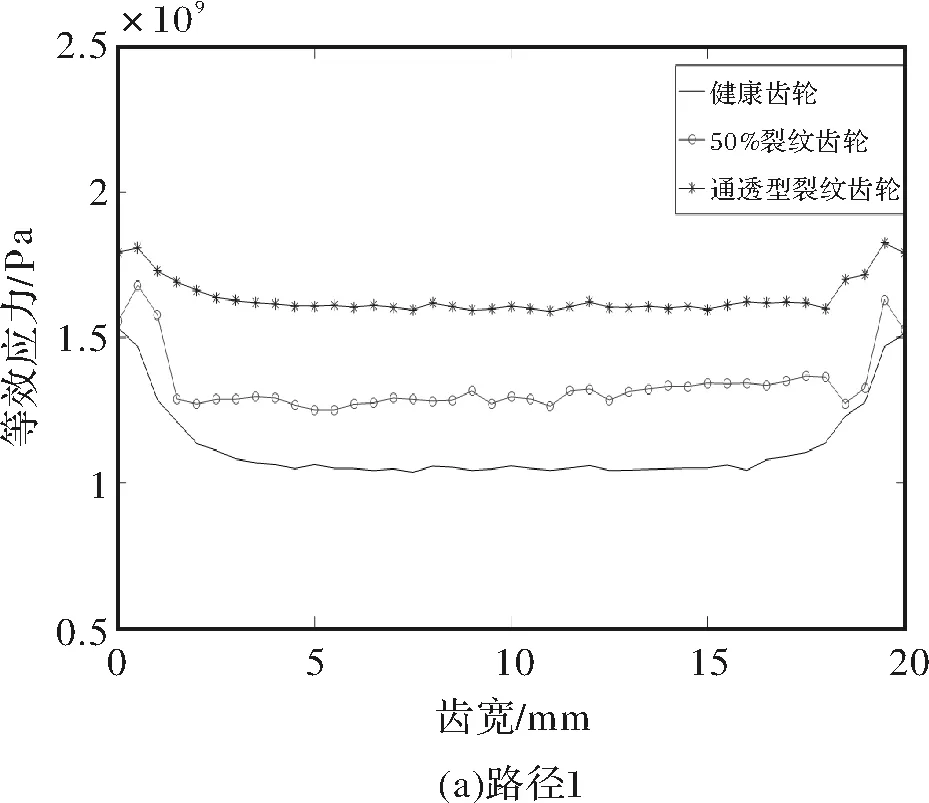
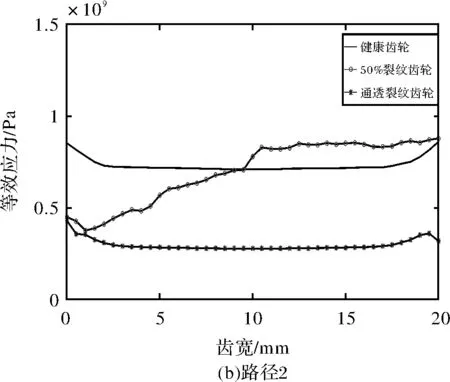
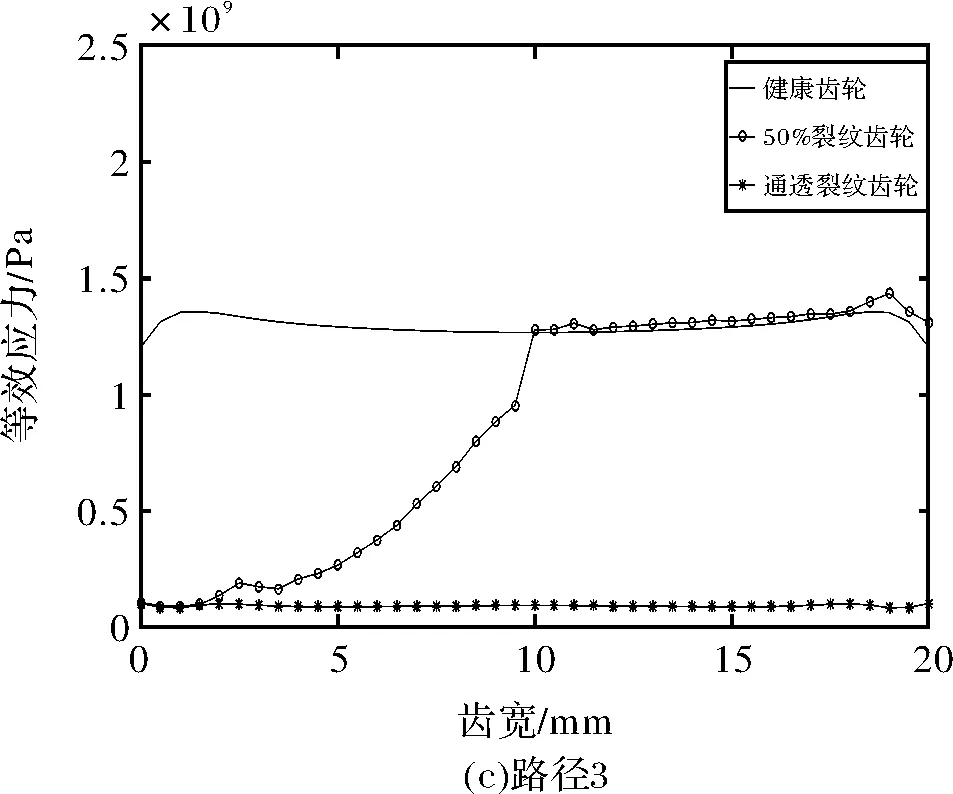
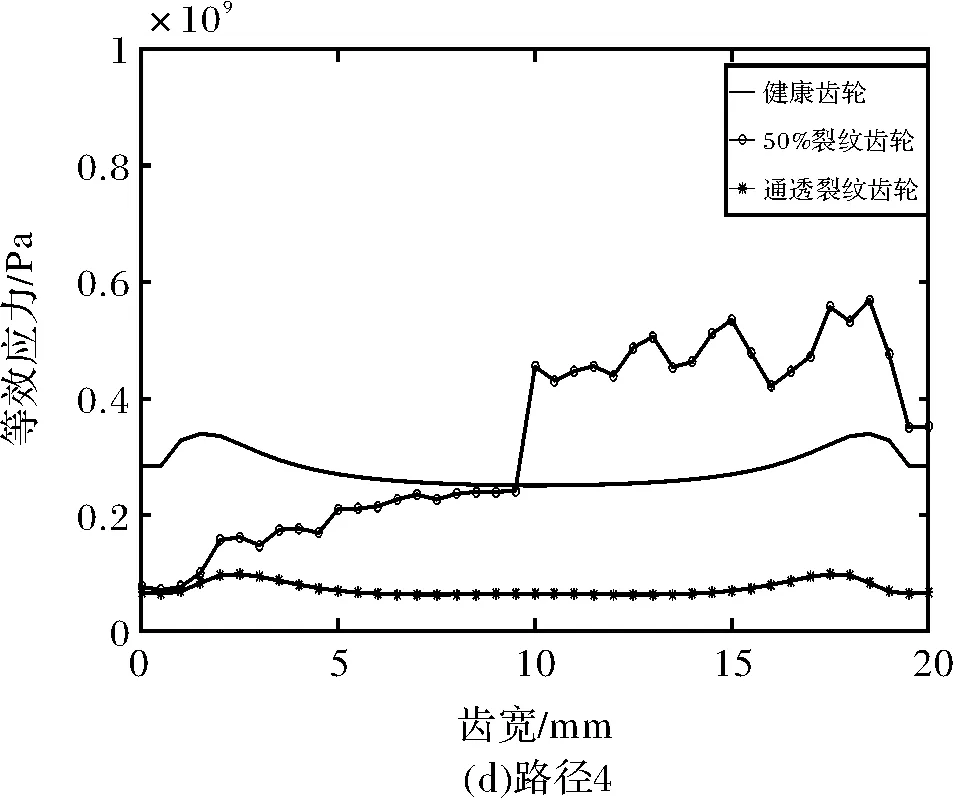
图11 不同路径下的等效应力
健康齿轮的总位移分布沿齿宽方向也是不均匀的,在两端齿边缘的位移大于齿中间部位的位移如图12所示。对于非穿透型裂纹来说,路径1和2的位移变化趋势与健康齿轮相似,如图12a、图12b所示,但路径3和4裂纹部分(即齿宽在0~10 mm处)的位移大于健康部分的位移的,如图12c、图12d所示。在通透型裂纹齿轮下,除路径1以外的所有路径上的总位移都大于健康齿轮的总位移。
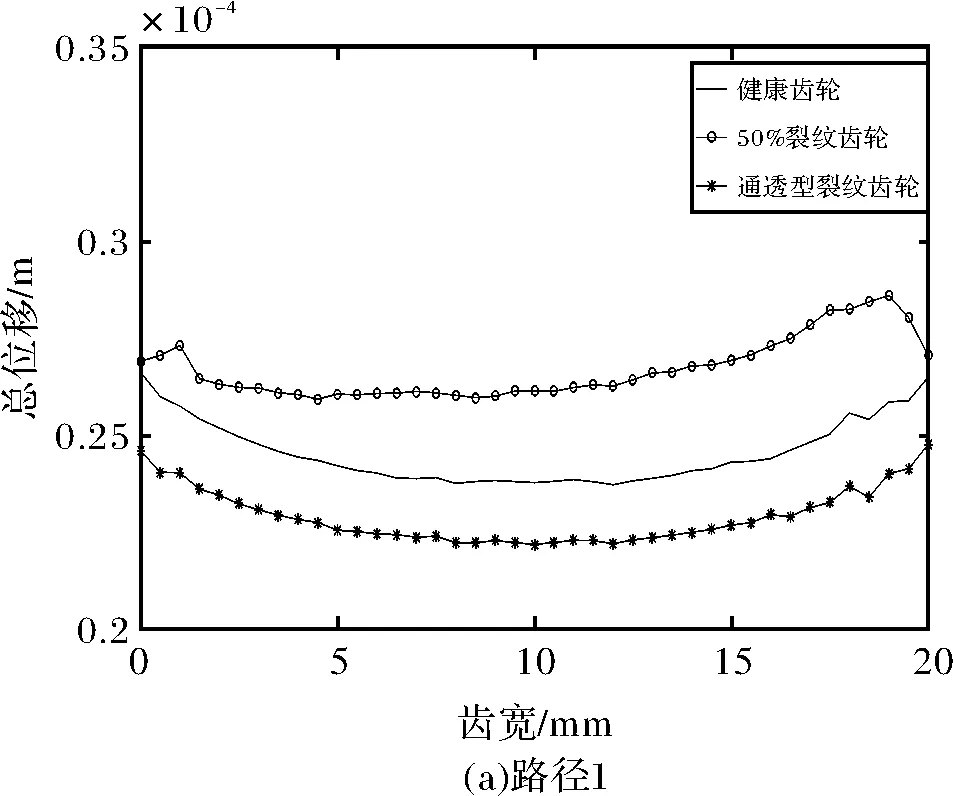
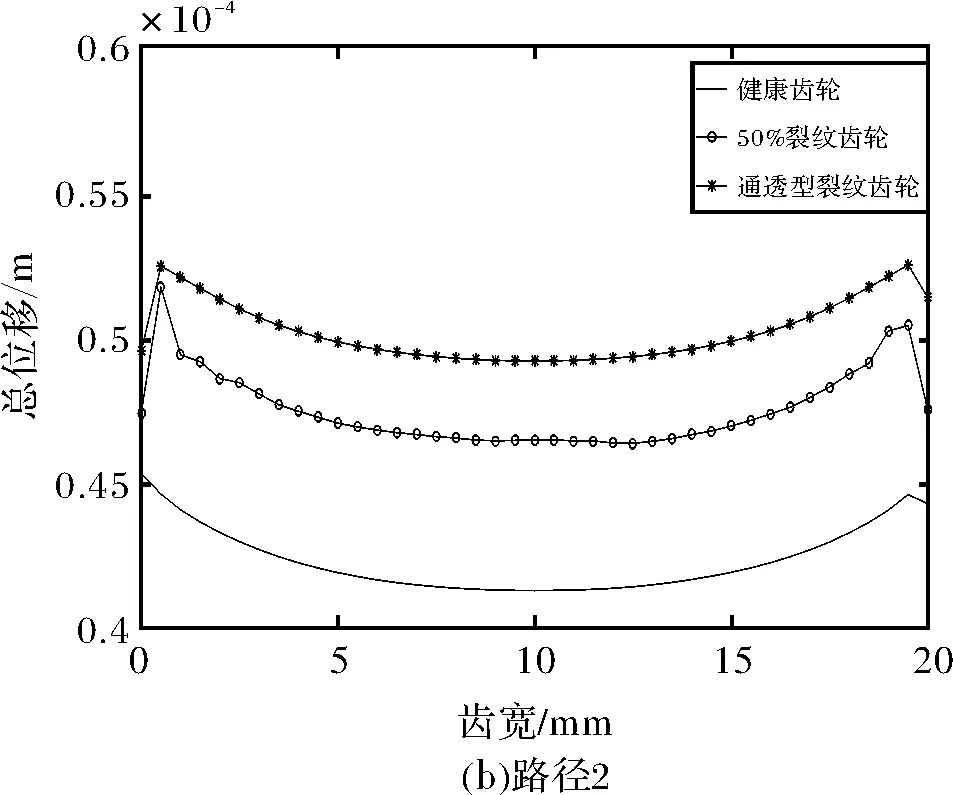
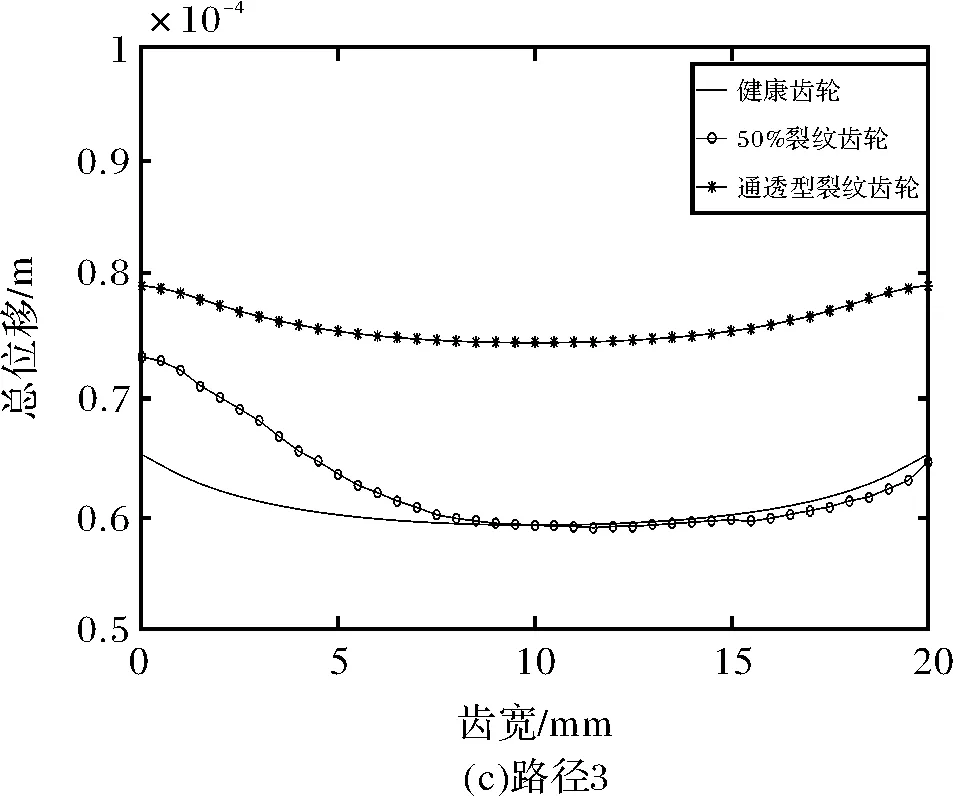
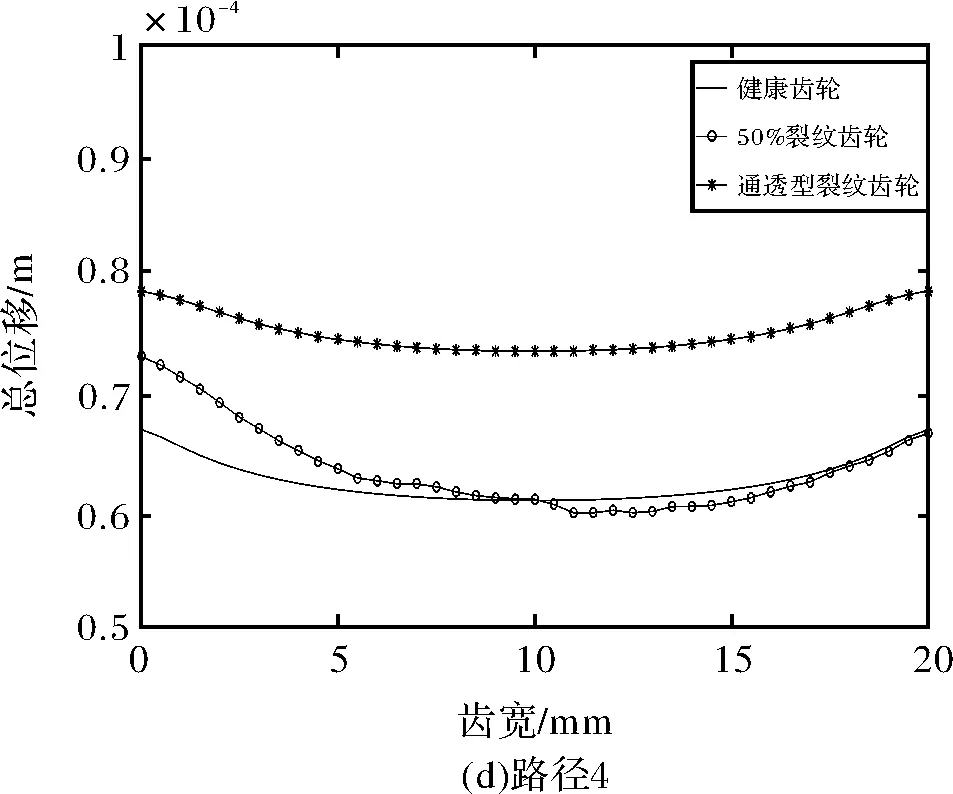
图12 不同路径下的总位移
5 结论
(1)对非穿透型齿根裂纹扩展的模拟得到了齿根裂纹的扩展路径,并且应力强度因子随着裂纹穿透程度的增大而增大,而KⅠ的增加幅度远远大于KⅡ的增加幅度。由于KⅠ明显大于KⅡ,表明了齿轮的断裂主要受Ⅰ型裂纹的影响。
(2)随着裂纹在齿宽方向上穿透程度的增加,齿轮副的啮合刚度随之减小。裂纹的穿透程度从0增加到50%的过程中,啮合刚度的减小幅度较小;当裂纹的穿透程度达到50%以上时,齿轮啮合刚度的减小幅度明显增大。
(3)对于齿廓方向上裂纹尾部的不同高度hi对啮合刚度的影响,没有齿宽方向上裂纹长度Lc对啮合刚度的影响显著。随着裂纹尾部高度的增加,啮合刚的减小幅度明显小于不同穿透程度的裂纹齿轮啮合刚度的减小幅度。
(4)在通透型裂纹齿轮下的等效应力、总位移的分布与健康齿轮的分布趋势相似;在非穿透型裂纹齿轮下的等效应力和总位移波动较大些,表明了非穿透型裂纹是齿轮加载分布不均匀。
