求解最大团问题的并行多层图划分方法

顾军华，霍士杰，武君艳，尹 君，张素琪

(1.河北工业大学 人工智能与数据科学学院，天津 300401； 2.天津商业大学 信息工程学院，天津 300134)(*通信作者电子邮箱zhangsuqie@163.com)

0 引言

最大团问题(Maximum Clique Problem, MCP)是经典的组合优化问题，属于NP(Non-deterministic Polynomial)完全问题[1]。很多重要的NP问题如无序树同构问题、子图同构问题等都可以转化为最大团问题，在实践中也有广泛的应用，如图像处理[2]、生物计算[3]、信号传输[4]、社会网络分析[5]、故障诊断[6]等，对最大团问题的研究具有较高的理论价值和现实意义。

在大数据时代下，实际图中节点的海量性和分析的复杂性，对最大团问题的研究在速度和精度上都提出了更高的要求，而目前有关求解最大团的相关算法比如回溯法[7]、分支限界法[8]、蚁群算法[9]、顺序贪婪算法[10]和遗传算法[11]等，都无法直接用于大型实例的求解。因此，将搜索空间进行划分，并行独立运算求解子空间的最大团结构成为一个可行的方案。

图划分也是个NP问题，在很多研究领域都有广泛的应用。基于启发式规则的KL(Kernighan-Lin) 算法[12]将图随机化成两等份，并逐步改善以减少割边。FM(Fiduccia-Mattheyses) 算法[13]对KL 算法进行了改进，采用单点移动，并引入了桶列表数据结构，减少了时间复杂度。后来Karypis等[14]提出基于heavy-edge heuristic的多层图划分，通过粗糙化将大图归约进行随机划分，通过反粗糙化以及优化技术还原划分。上述图划分算法尝试将图中的节点集划分成一定数量的规模相近的子集，以最大限度地减少割边。这些方法提高了分图的收敛速度，但是会破坏图信息的完整性。随着图规模的大幅增加，求解最大团问题时不仅需要较快的收敛速度，在图划分阶段还不应该破坏团结构，因此上述划分图的策略并不适合于大规模图的最大团问题求解。

针对上述问题，Wu等[15]提出一种单层图划分方法(Single Graph Partitioning method, SGP)求出图中所有点的导出子图，并且利用MapReduce架构实现了SGP，针对每一个点的导出子图，采用分支定界算法枚举各个子图中的最大团，但是该算法没有考虑负载均衡，同时会产生重复的、不准确的中间输出数据，需要额外的处理过程删除重复数据、甄别正确结果。Xiang 等[16]提出基于MapReduce并行求解最大团的算法，该算法采用着色分图，使用分支定界算法并行独立求解各个子图的最大团；但是应用该算法求得的子图数量过多、规模较大，求解各个子图最大团的时间复杂度和空间复杂度高，并且该文并未给出大规模图的划分结果。Svendsen等[17]提出了基于密钥的并行求解最大团的算法，该算法是对Wu 等[15]提出方法的改进，主要对分支定界算法进行改善，采用并行枚举各个子图的最大团，有效地解决了负载均衡问题；但是该算法求解的子图规模较大，并且分支定界算法枚举最大团的效率较低。Mukherjee等[18]提出了基于MapReduce并行求解二分最大团的算法，该算法将大规模图例转化为小规模图例，通过对搜索空间的剪枝操作，降低了子图搜索的冗余。该算法通过对所有节点度排序，进行合理的任务分配，从而平衡了集群的负载，最后该算法使用枚举的方法求得所有的二分最大团。

尽管上述算法使得在大规模图例上求解最大团成为了可能，但是，MapReduce编程模型需要频繁地进行I/O操作，无法充分地利用内存，而且任务的调度和启动的开销较大，因此MapReduce编程模型并不适合做迭代式的算法。而Spark平台是一种基于内存的编程框架，具有容错性高、执行速度快的优点，Spark的GraphX图计算框架有着丰富的API，在对大规模图例的计算时，具有速度快、操作简单的优点，因此本文提出求解最大团问题的并行多层图划分方法(Parallel Multi-layer Graph Partitioning method for Solving Maximum Clique, PMGP_SMC)。首先，本文提出了多层图划分(Multi-layer Graph Partitioning, MGP)方法，在文献[15]、文献[17]所采用的SGP的基础上，对图中的节点按度排序，在保持图中原有团结构不变的情况下大幅度减少子图规模，并对规模较大的子图进行多层图划分，进一步缩小子图规模，为了对大规模图例进行图划分，本文应用Spark的GraphX图计算框架实现MGP形成并行的多层图划分(Parallel MGP, PMGP)方法。然后，考虑到对图进行最大团问题的求解在速度和精度方面的要求，本文选取了基于惩罚值的局部搜索算法(Local Search algorithm Based on Penalty value, PBLS)求解最大团问题，由于PMGP可以将大规模图例分图产生很多小规模子图，因此本文根据子图的规模优化了PBLS的迭代次数，提出基于速度优化的PBLS(PBLS based on Speed optimization, SPBLS)，对划分后的各个子图，使用SPBLS独立求解各个子图的最大团。最后，将PMGP和SPBLS相结合，形成求解最大团问题的并行多层图划分方法(PMGP_SMC)。为了验证算法的有效性，本文应用Spark的GraphX图计算框架实现SGP形成并行的SGP(Parallel SGP, PSGP)，并且将PSGP和PBLS相结合形成求解最大团问题的PSGP(PSGP for Solving Maximum Clique, PSGP_SMC)。极大团枚举(Maximal Clique Enumeration, MCE)是一种暴力求解最大团问题的方法，该方法虽然可以精准求出子图的最大团，但效率低下。为了比较求解最大团问题的准确性，本文将PMGP与极大团枚举方法相结合形成基于MCE求解最大团问题的并行多层图划分方法(Parallel Multi-layer Graph Partitioning for solving maximum clique based on MCE, PMGP_MCE)。实验结果表明，与PSGP_SMC相比，PMGP_SMC可以更快地求解各个子图的最大团，与PMGP_MCE相比，PMGP_SMC可以高效精确地求解各个子图的最大团。

1 多层图划分方法

1.1 最大团基本定义

定义1 完全子图。称U=(V′,E′)是无向图G=(V,E)的完全子图，当且仅当对于任意给定的无向图G=(V,E)，若V′ ⊆V，E′ ⊆E，且对于∀u,v∈V′，有(u,v) ∈E′。

定义2 团。称无向图G的完全子图U是G的一个团，当且仅当完全子图U不包含在图G的更大完全子图中。

定义3 最大团。称无向图G的最大团C为图中包含顶点数最多的团，最大团问题即求解图G=(U,V)的最大团C。

1.2 MGP流程

Wu等[15]提出了单层图划分方法(SGP)，该方法根据图中各个节点及其邻接点之间的相连关系产生导出子图，然后针对每个子图进行最大团的求解。该算法在不破坏最大团结构的前提下，可以将大规模图例分解为小规模图例，然后对小规模图例并行求解最大团。假设存在图G=(V,E)，依次选取V中的顶点vi，构造子图Gi=(V′,E′)。SGP的具体流程如下:

步骤1 初始化顶点V′和边集合E′为空，将vi和节点vi的邻接节点集合加入V′。

步骤2 依次选择顶点集合V′中的节点i和节点j，如果边(i,j)∈E，则将边(i,j)添加到E′当中，直到遍历完顶点集合V′，完成子图Gi的构建。

SGP生成的子图规模主要取决于起始节点的度，但在大规模图中节点的度往往差异较大，生成子图的规模也相差较大，导致求解最大团时因负载不均衡将耗费大量时间。为了克服这些不足，本文提出MGP，在单层图划分的基础上基于节点的度对节点进行排序，在构建子图时删除度数值较起始节点vi低的节点(在度数相等时，删除节点编号小于vi的节点)，在保持原有的团结构不变的情况下，利用排序大幅度减小子图规模，并且针对规模较大的图进行多层图划分，以平衡求解最大团时的任务负载。假设存在图G=(V,E)，依次选取V中的顶点v，构造子图Gv=(Vv,Ev)。MGP的具体流程如下：

步骤1 首先随机给节点编号1,2，…，m(m为节点的个数)，初始化顶点Vv和边集合Ev为空。

步骤2 首先求得v的邻接点集合vList，vList中的任意节点vertex满足如下两个条件：①vertex节点度数大于v的度数；②vertex节点度数等于v的度数，但vertex节点的编号大于v节点的编号。将节点v和vList集合中的节点加入Gv的顶点集合Vv。

步骤3 依次选择顶点集合Vv中的节点i和节点j，如果边(i,j)∈E，则将边(i,j)添加到Ev当中，直到遍历完顶点集合Vv，完成子图Gv的构建。

步骤4 若子图Gv中节点个数大于一定的阈值(设为300)，则继续对子图使用步骤5进行多重图划分，否则，算法结束。

步骤5 依次选择子图Gv中的节点u构建子图Gu=(Vu,Eu),首先得到u的邻接点集合uList，uList中的任意节点vertex满足如下两个条件：①vertex节点度数大于u的度数；②vertex节点度数等于u的度数，但vertex节点的编号大于u节点的编号,将节点u和uList集合中的节点加入Vu。依次选择顶点集合Vu中的节点i和节点j，如果边(i,j)∈Ev，则将边(i,j)添加到Eu当中，直到遍历完顶点集合Vu，完成子图Gu的构建。

MGP的关键在于步骤2并没有将v和v的全部邻接节点加入Gv，只选择了满足①和②条件的邻居节点，为了证明这样不会破坏原图G的团结构，只需证明图G的任意一个团结构都包含在MGP构造的某个Gv中。本文给出了定理1进行说明，具体如下。

定理1 利用MGP进行图划分，图G中所有团结构将被保留到各个子图当中。

证明 对于图G=(V,E),C= (Vc,Ec)是图中任意的一个团，假设团C中存在点v，v满足在原图G当中度数最小(当团C中存在有多个节点满足这个条件时，选择节点编号最小的节点)。根据MGP，构造以点v为诱导节点的子图Gv(图Gv中的节点在原图G中的度数大于v，或者节点编号大于v),对于∀u∈Vc，u节点在原图G中的度数大于v或者在度数相等时，u节点编号大于节点v，故u∈Gv，以此类推，团C中的所有节点均包含于Gv，即图中所有的团结构都被保留在各个子图中。

得证

为了进一步说明MGP不会破坏原图的团结构，本文以图1为例说明，其中图1(a)示例图G包括3个团，分别如图1(b)、图1(c)和图1(d)所示。以图1(b)为例，在{2,3,5}节点集合中，节点5在图1(a)中的节点度数最小。依据MGP得到的图划分如图2所示，其中加黑的点表示针对该节点的分图产生的子图。针对5节点的子图为图2(e),很明显可以看出，图1(b)中的节点均位于图2(e)中，同理，图1(c)中1节点的序号最小，图1(c)中的节点均位于针对1节点的子图(图2(a))中，图1(d)中6节点的度数最小，图1(d)中的节点均位于针对6节点的子图(图2(f))中，因此MGP不会破坏原图的团结构。

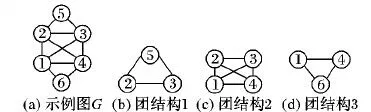
图1 示例图G及其团结构Fig. 1 Example graph G and its clique structures

以图1(a)为例对比SGP和MGP两种分图方法的性能。根据MGP的流程对图G的划分结果如图2所示，根据SGP的流程对图G的划分结果如图3所示。针对图G，SGP求得的子图的平均节点个数为4.33，节点个数最多为5；而MGP求得子图的平均节点个数为2.67，节点个数最多为4，因此在不影响求解最大团的基础上，MGP对子图的划分规模明显低于SGP。

图2 MGP图划分结果Fig. 2 Graph partitioning results of MGP

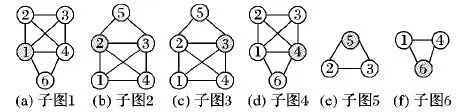
图3 SGP图划分结果Fig. 3 Graph partitioning results of SGP

2 并行多重图划分方法

为了在大规模图例上进行图划分，本文应用GraphX图计算框架实现MGP形成并行的多层图划分方法(PMGP)，并将PMGP框架部署到Spark分布式云计算平台上。下面首先介绍Spark和GraphX的特点，并给出GraphX框架的常用方法，然后详细说明PMGP的实现过程和伪代码。

2.1 Spark和GraphX

Spark是基于内存计算的大数据分布式计算框架，是一种快速、通用、可扩展的大数据分析引擎，它拥有Hadoop平台和MapReduce框架的全部优点，但不同的是Spark运算的中间结果能存储在内存中，而不再需要读写Hadoop分布式文件系统(Hadoop Distributed File System, HDFS)，提高了并行计算的速度，因此Spark更适合进行数据挖掘与机器学习等需要迭代处理的算法[19]。目前，Spark生态系统已经发展成为一个包含多个子项目的集合，包含SparkSQL、Spark Streaming、MLlib、GraphX等子项目,其中GraphX是图结构数据的并行处理系统。基于数据并行引擎 Spark，GraphX采用了顶点分割策略，一个图的顶点和边都带有属性并且可以使用两个弹性分布式数据集顶点RDD和边RDD来表示。因此，GraphX对图并行计算和数据并行计算进行了结合，使得其在计算速度上能够和专业的图计算系统相媲美，同时还保留了数据并行系统的表达力,可以方便且高效地完成图计算的一整套流水作业。图的应用程序编程接口(Application Programming Interface, API)方法有很多种，包括图的构建、更改图的顶点和边的属性值、统计图的结构信息等，其中并行多层图划分方法(PMGP)用到的API方法如表1所示。

表1 GraphX图计算方法Tab. 1 GraphX graph calculation method

2.2 PMGP流程

PMGP的步骤如下：

1)数据预处理。对与寻找最大团来说，图中的重复边以及自循环的边都会影响最终的求解过程，因此首先要进行数据预处理过程。数据预处理主要是对文本数据的操作，首先应用Spark的textFile算子从HDFS中读取数据，其次使用filter算子去掉自循环的边和重复的边，最后针对过滤后的数据先进行map操作将RDD中的数据转换为Edge类型，再使用GraphX图计算框架的fromEdges方法生成图Graph1，其中图Graph1包括顶点RDD和边RDD，具体的流程如图4所示。

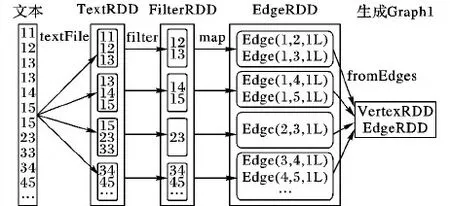
图4 数据预处理RDD转化图Fig. 4 RDD transformation graph of data preprocessing

2)获取图的必要参数。在步骤1)得到图Graph1的基础上，使用GraphX的degrees方法获取DegreeRDD，使用collectNeighborIds方法获取NeighborRDD。

3)针对每一个节点寻找满足条件的邻居节点。在步骤2)获取DegreeRDD以后，使用DegreeRDD和GraphX的outerJoinVertices方法将图Graph1的顶点属性更新为每一个节点的度数，然后使用aggregateMessages方法寻找每一个节点满足条件的邻居节点。aggregateMessages可以并行化地对图中的每一个triplet进行操作,triplet的定义如图5所示。在GraphX中，triplet表示一个五元组，包括源点编号srcId、源点属性srcAttr、目的点编号dstId、目的点属性dstAttr和边的属性attr。在sendMsg阶段，根据MGP图划分方法，当图Graph1的顶点属性变为顶点的度数时，当scrAttr>dstAttr或者当srcAttr=dstAttr但srcId>dstId时，就向目的顶点发送源顶点的srcId，否则就向源顶点发送dstId。在mergeMsg阶段，针对每一个节点，将收到的消息进行合并形成满足条件的邻居节点集合，该方法最终返回VertexRDD类型的EligibleRDD，其顶点的属性为每一个节点满足条件的邻居节点集合。

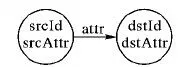
图5 triplet类型的定义Fig. 5 Definition of triplet type

4)针对每一个节点构造子图。调用aggregateMessages方法生成子图，在发送消息阶段，分为如下两步：①当源节点的度数大于目的节点的度数或两者度数相等但源节点的编号大于目的节点的编号时，按照MGP的步骤3，依次遍历源节点的每一个邻居节点temp，如果目的节点满足条件的邻居节点集中出现过的节点temp，则节点temp和源节点之间形成一条边，当遍历完源节点所有的邻居节点以后，将生成的子图发给目的节点。②当源节点的度数小于目的节点的度数或两者度数相等但源节点的编号小于目的节点的编号时，则依次遍历目的节点的每一个邻居节点temp，如果源节点满足条件的邻居节点中包含temp，则在temp节点和目的节点之间添加一条边，当遍历完目的节点的所有邻居节点以后，将生成的子图发给源节点。在合并消息阶段，每一个节点将收到的消息进行合并即可。该方法最终返回VertexRDD类型的EligibleSubGraphRDD，其顶点的属性为每一个节点产生的子图。

5)进行多重图划分。使用filter算子从EligibleSubGraphRDD中过滤出节点规模大于300的子图，按照MGP的步骤5，使用map算子对大于300个节点规模的子图进行多重图划分，得到VertexRDD类型的Last_Eligible_SubGraphRDD，即为最终划分的结果。

PMGP的伪代码如算法1所示。

算法1 PMGP。

输入 文本文件的输入路径input；

输出 满足条件的子图。

1)

数据预处理得到EdgesRDD

2)

Graph1 ← Graph. fromEdges(EdgesRDD)

3)

使用degrees和collectNeighborIds得到DegreeRDD和

NeighborRDD

4)

Graph2←Graph1.outerJoinVertices(DegreeRDD).

outerJoinVertices(NeighborRDD)

5)

依据第3)步得到EligibleRDD

6)

Graph3← Graph2.outerJoinVertices(EligibleRDD).

outerJoinVertices(NeighborRDD)

7)

依据第4)步构造每一个节点的子图，得到

EligibleSubGraphRDD

8)

依据第5)步对大于300个节点规模的子图进行多重图划

分，得到Last_Eligible_SubGraphRDD

9)

Last_Eligible_SubGraphRDD即为求得的子图，算法结束

按照PMGP的流程，GraphX环境下的RDD转化图如图6所示。

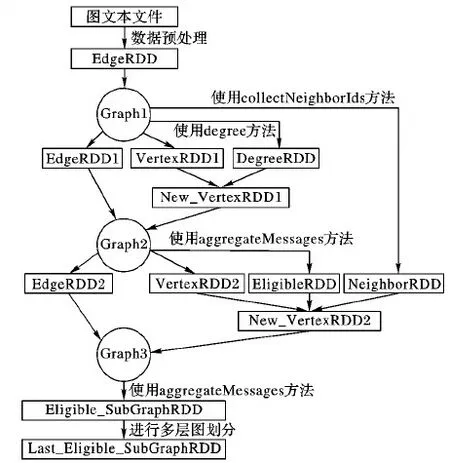
图6 PMGP的RDD转化图Fig. 6 RDD transformation graph of PMGP

2.3 PMGP的实验结果

为了说明图划分的有效性，本文选取了表2所示的Stanford Large Network Dataset Collection作为测试图例，该数据集是研究和分析大规模图数据的常用图例。作为对比，本文应用Spark的GraphX图计算框架实现并行单层图划分方法(PSGP)。对多个图例进行并行多层图划分的实验结果如表3所示，其中：Max表示划分后子图的最大规模(子图中的最大节点数)，Avg表示子图的平均规模，ρ表示子图的平均密度。对于每一个子图Gi的密度ρi计算如式(1)所示：

ρi=|E|/(|V|*(|V|-1))

(1)

其中:|V|表示子图Gi的节点个数;|E|表示子图Gi的边数。

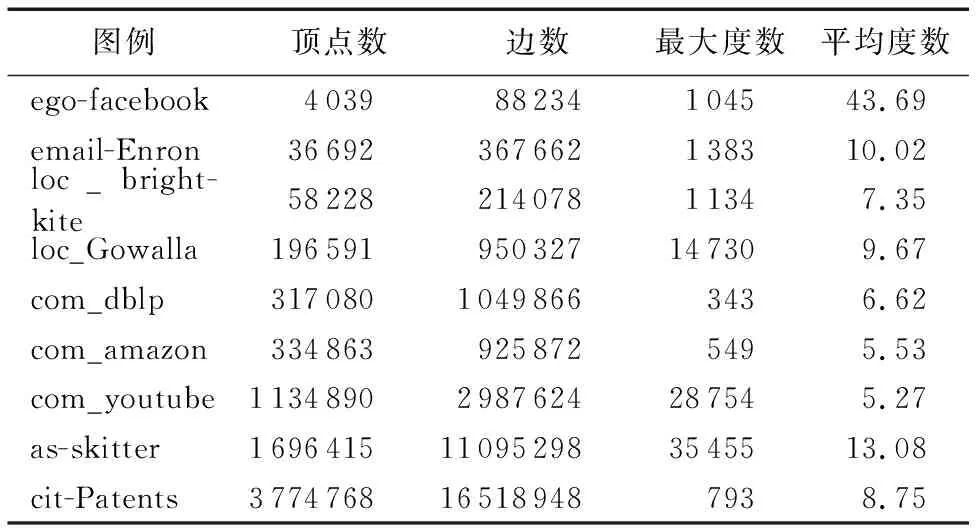
表2 测试图例的基本属性Tab. 2 Basic attributes of test graph examples

子图的平均密度计算如式(2)所示:

(2)

其中N表示原图G的节点个数。

从表3可以看出，PMGP在所有的数据集上求得的最大子图规模相较于PSGP要小得多。在as-skitter网络上，PSGP求得的最大子图规模为35 456，而PMGP求得的最大子图规模为232，是PSGP的1/150左右；在com_youtube网络上，PMGP求得的最大子图规模是PSGP的1/170左右。此外，在所有的数据集上，PMGP求得的子图的平均密度相比PSGP也较小，即划分的子图更加紧凑。综上所述，PMGP在不影响求解最大团的基础上，减少求解最大团时的搜索空间规模。

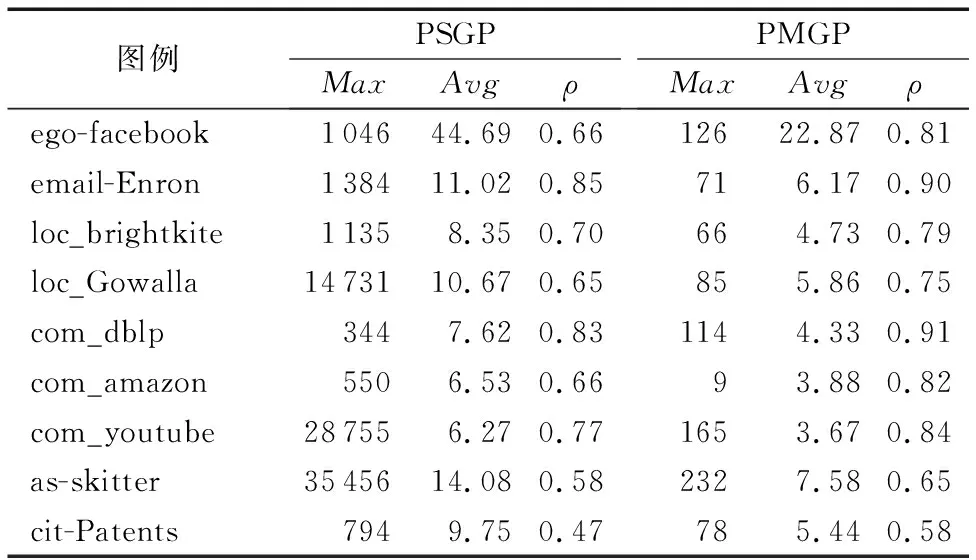
表3 PSGP和PMGP图划分的实验结果Tab. 3 Experimental results of PSGP and PMGP graph partitioning

3 基于速度优化的惩罚值局部搜索算法

在完成图划分后，需要分别求得的每个子图的最大团，再得到整个图的最大团，最大团问题的早期研究主要采用确定性算法，如枚举法、分支定界法等，但最大团问题求解的复杂度会随着图规模增大呈指数级增长，确定性算法不适合求解大规模图例的最大团问题，因此，本文选取了复杂度较低，执行速度快的局部搜索算法来求解最大团问题。PBLS[20]是本团队之前提出的较好的局部搜索算法，由于PMGP产生的子图规模较小，为了增加PBLS的灵活性，本文提出基于速度优化的惩罚值局部搜索算法(SPBLS)。

3.1 SPBLS

张素琪[20]在Random_BLS(Random Breakout Local Search for maximum clique problems)算法[21]的基础上提出了基于惩罚值的PBLS，该算法在局部搜索过程中根据各节点的禁忌值和惩罚值对节点进行选择，禁忌值和惩罚值在每次迭代后更新。首先，图中各节点的禁忌值和惩罚值初始化为0。局部搜索时从候选集中选择不被禁忌且惩罚值最小的点加入CurrentClique(如果这样的点有多个，从其中随机选择)，局部搜索结束后更新禁忌值和惩罚值。对节点进行禁忌和惩罚可增强搜索过程的多样性，使得未被搜索到即未加入过团的点有更多的添加可能。

尽管PBLS在求解最大团问题时复杂度低、执行速度快，但是PBLS的迭代次数需要人为设定，算法运行的迭代次数越多，求解的准确率越高。图7是使用PMGP对as-skitter图例划分产生的子图分布，其中，横坐标代表as-skitter产生的各个子图的节点个数(即子图的规模)，纵坐标表示as-skitter产生的各种子图规模下的子图个数占子图总个数的百分比。从图7可以看出， PMGP可以对大规模图例分图产生较小的子图，对as-skitter图例来说，约97%的子图规模都在70个节点以下。在使用PBLS对PMGP产生的子图并行求解最大团时，为了保证规模较大的子图可以准确地求解出最大团，PBLS需要设定较高的迭代次数，但是，对于小规模的子图，通常只需要很少的迭代次数就可以求解出比较好的结果，这样就导致PBLS在求解小规模图例的最大团时，时间效率较低。因此为了增加PBLS的灵活性，提高算法的执行速度，本文根据子图的规模优化PBLS的迭代次数提出了SPBLS。

SPBLS的迭代次数的定义如式(3)所示:

(3)

其中:T表示最大迭代次数;N表示图中节点的个数;m是取值在10到100之间的常量;c是取值在0到1之间的常量。式(3)表明当图中的节点个数越多时，SPBLS求解最大团所需要的迭代次数越多，当求得的迭代次数为小数时，迭代次数向上取整。为了进一步验证式(3)的有效性,本文求出了300个节点以内的子图所需的迭代次数分布,如图8所示,这里m取值为50，c取值为0.5，T取值为15。从图8可以看出，随着子图规模的不断增大，SPBLS运行的迭代次数也不断增加，该算法保证了较小规模子图使用较少的迭代次数，较大规模子图使用较多的迭代次数。

图7 PMGP在as-skitter上产生的子图规模分布Fig. 7 Subgraph scale distribution generated by PMGP on as-skitter

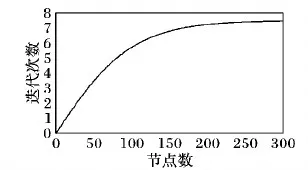
图8 SPBLS的迭代次数分布Fig. 8 Iteration number distribution of SPBLS

为了进一步验证SPBLS的有效性，本文从as-skitter图例产生的子图中分别取出50个节点规模的子图、100个节点规模的子图、150个节点规模的子图和200个节点规模的子图，分别使用PBLS求解最大团，对比PBLS在求解到最大团时所需的迭代次数和SPBLS依据节点规模所求的迭代次数，其结果分别如图9所示。

从图9可以看出，随着子图规模不断增加，算法求解到最大团所需的迭代次数也在不断增加。从图9(a)可以看出，对于50个节点规模的图例，应用PBLS求解最大团时，迭代到2次时，最大团的规模已经不再发生变化，对于SPBLS来说，应用式(3)可以求得50节点规模的子图大约需要3次迭代，因此PBLS在求解到最大团时所需的迭代次数和SPBLS依据节点规模所求的迭代次数是几乎相同的，使用SPBLS不会影响求解最大团的精度。从图9(b)可以看出，对于100个节点规模的子图，PBLS运行6次迭代，最大团规模就已经不再变化，而对于SPBLS，依据式(3)，100个节点规模的子图大约需要6次迭代，因此SPBLS也不影响求解最大团的精度。同理，从图9(c)和图9(d)也可以看出，在150个节点规模和200个节点规模的子图上，SPBLS也不影响求解最大团的精度。综上所述，SPBLS保证了在不影响求解最大团精度的前提下，对小规模子图使用较少的迭代次数，较大规模子图使用较多的迭代次数，从而依据子图规模动态调整迭代次数，提高算法的整体效率。

图9 不同节点规模PBLS求解最大团的迭代次数变化Fig. 9 Iterative number change in solving maximum clique of PBLS at different node scales

3.2 SPBLS的伪代码

SPBLS的伪代码算法2所示。

算法2 SPBLS。

输入 图G(V,E)，最优团更新次数t，禁忌参数基本值φ,定向扰动概率的阈值P0，随机扰动幅度α；

输出 图G的最大团BestClique。

从图G中随机选取点v，加入当前团CurrentClique中，初始化最大扰动强度Imax为|V|的0.1倍，最小扰动强度Imin为顶点数的0.01倍，当前迭代次数numsteps为0，初始化所有点的禁忌值和惩罚值为0，最优团未更新次数w为0，初始化算法求得最大团RbestClique为空,初始化最大团BestClique为空；

按照式(3)计算图G所需的迭代次数maxsteps

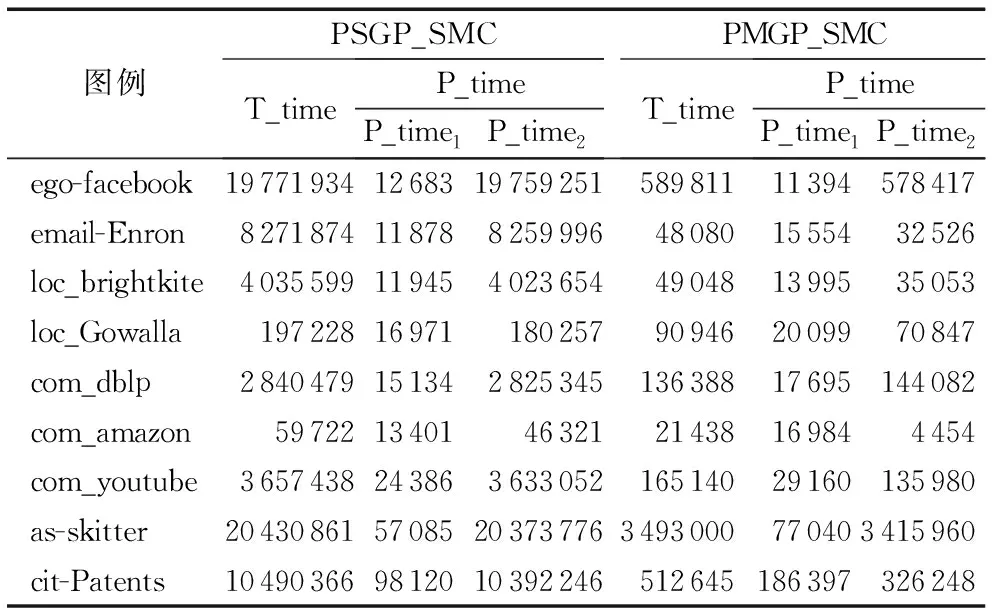
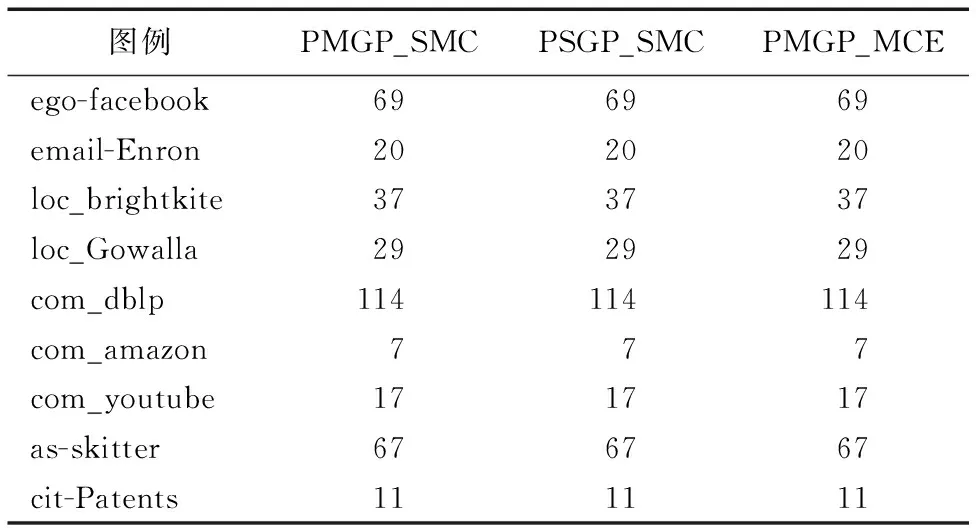
while(numsteps

向RbestClique加入节点；

if(RbestClique.length>BestClique.length) then

BestClique←RbestClique；

w←0；

else

w←w+1

end if

初始化Clique_local为空；

if(w>T) then

w←0；

以Imax的强度在CurrentClique上执行随机扰动，更新节点的

禁忌值和惩罚值；

CurrentClique中的节点加入Clique_local;

else

perturbSte←0;

ifClique_local==CurrentCliquethen

perturbSte←perturbSte+1;

else

perturbSte←Imin；

end if

依据定向扰动概率P0计算概率P；

产生从0到1的随机数k；

if(p≤k)

以perturbSte的强度在Clique上执行定向扰动，更新所有

节点的禁忌值和惩罚值；

CurrentClique中的节点加入Clique_local;

else

以perturbSte的强度在Clique上执行定向扰动，更新所有

节点的禁忌值和惩罚值；

CurrentClique中的节点加入Clique_local;

end if

end if

end while

得到最大团BestClique，算法结束。

4 实验结果与分析

本次实验将PMGP和SPBLS相结合，形成求解最大团问题的并行多重图划分方法(PMGP_SMC)。为了验证PMGP_SMC在求解最大团问题的高效性和准确性，本文应用Spark的GraphX图计算框架实现SGP形成并行的单层图划分方法(PSGP)，并且将PSGP和PBLS相结合形成求解最大团问题的并行单层图划分方法(PSGP_SMC)，将PMGP与极大团枚举(MCE)方法相结合形成基于极大团枚举求解最大团问题的并行多重图划分方法(PMGP_MCE)，并对3种算法在速度和精度方面作对比。实验采用表2所示的Stanford的9个大规模数据集[22]进行测试。PSGP_SMC在使用PBLS求解最大团时，由于SGP产生的子图规模较大，因此为了保证求解最大团的精度，本文将PBLS的迭代次数统一设置为20。SPBLS所需的迭代次数maxsteps依据式(3)确定，最大团未更新的最大次数t为maxsteps的一半，禁忌参数基本值φ为7,定向扰动概率的阈值P0为0.8，随机扰动幅度α为0.6。

本文使用了Spark 集群进行实验，其中包括1个master节点和5个worker节点。worker节点硬件配置如下：Intel Xeon Core E5-1620,CPU@3.70 GHz processor; 256 GB内存。软件配置如下：Linux CentOS 6.5，JDK1.7.0_67，Spark-1.6.2版本。

PMGP_SMC与PSGP_SMC两种算法的运行时间比较如表4所示，其中，T_time表示每一个大规模图例运行的总时间，P_time包括两部分，P_time1表示在图划分阶段的运行时间，P_time2表示在分阶段突破局部搜索求解最大团阶段的运行时间。由实验结果可知，由于PMGP_SMC方法进行了多重图划分，因此在图划分方面PMGP_SMC算法比PSGP_SMC慢，但由于PMGP_SMC算法求得的子图规模比较小，在使用SPBLS求解最大团时，能够依据节点个数动态调整算法的迭代次数，因此与PSGP_SMC算法相比，所需的迭代次数较少，速度较快，从总的时间来看，PMGP_SMC较PSGP_SMC有很大程度的改善。其中：在ego-facebook数据集上，PMGP_SMC算法的速度相比PSGP_SMC提高了33倍；在email-Enron，PMGP_SMC的速度提高了172倍；在其他数据集上，算法提高了几十倍不等。验证了PMGP_SMC有更快的速度和更高的效率。

表4 PMGP_SMC和PSGP_SMC运行时间比较 msTab. 4 Running time comparison of PMGP_SMC and PSGP_SMC ms

为了进一步验证求解最大团问题的有效性，本文将PMGP_SMC、PMGP_MCE和PSGP_SMC在求出的最大团规模方面作了对比，3种算法求得的最大团规模如表5所示。从表5可以看出，由于PMGP产生的子图规模较小，因此使用PMGP_SMC和PMGP_MCE求得最大团规模一致，但PMGP_SMC相比PMGP_MCE具有较高的求解效率；由于在求解最大团时，PSGP_SMC将迭代次数设置为20次，因此也可以求得比较好的结果，但与PMGP_SMC相比，该算法的执行速度较慢。因此与其他两种算法相比，PMGP_SMC算法在求解最大团问题时，具有高效性和准确性。

表5 不同算法求得的最大团规模对比Tab. 5 Maximum clique scale comparison of different algorithms

5 结语

并行图划分是大规模图例进行最大团问题求解的一个重要研究方向。针对求解大规模图的最大团问题中复杂度高、通用性差等问题，本文提出求解最大团问题的并行多重图划分方法(PMGP_SMC)。首先本文提出了MGP图划分方法，在SGP的基础上，对图中的节点按度排序，在保持图中原有团结构不变的情况下大幅度减少子图规模，并对规模较大的子图进行多重图划分，进一步缩小子图规模；然后，本文应用Spark的GraphX并行图计算框架实现MGP形成PMGP。此外，本文依据子图的规模优化了PBLS的迭代次数，提出了SPBLS，对划分后的各个子图，分别使用SPBLS并行求解各个子图的最大团。最后，将PMGP和SPBLS相结合，形成求解最大团问题的并行多重图划分方法PMGP_SMC。实验证明，与PSGP_SMC和PMGP_MCE相比，PMGP_SMC可以有效地处理数以百万节点的图例，高效精准求解大规模图例的最大团，为其他组合优化问题的高效求解带来启示。