基于结构洞和度折扣的影响力最大化算法

李敏佳，许国艳，朱 帅，张网娟

(河海大学 计算机与信息学院，南京 211100)(*通信作者电子邮箱1256868536@qq.com)

0 引言

随着信息化和互联网的快速普及，社交网络在信息传播、思想交流等方面有着举足轻重的地位。由于社交网络的日益深入，以影响力最大化(Influence Maximization, IM) 问题为主要应用的需求也逐步增长[1]。如何选取部分节点，通过这些节点在网络中扩散使得最终影响的节点数目最多，成为当前需要解决的问题[2]。

Kempe等[3]详尽地描述了经典的信息传播模型并验证了影响力最大化问题是NP(Non-deterministic Polynomial)-hard问题，在此基础上，提出来性能至少是最优解63%的贪心算法来解决这一难题;但是贪心算法时间开销较大，难以很好地应用在规模较大的网络平台上。之后，Chen等[4]提出了New Greedy算法和Mix Greedy算法来优化贪心算法；然而，优化后的贪心算法时间消耗仍很高，很难应用到大型社交网络中。

近年来出现了大批的启发式算法来改善贪心算法效率低下的情况。Chen等[4]提出DegreeDiscount算法来克服基于Degree算法的局限性，该算法是当某个节点被存储在种子节点集合中时，在计算其邻居节点的度时要打一定的折扣。文献[5]针对筛选度数最大的节点而造成影响重叠问题提出了一种覆盖贪心算法(Set Covering Greedy algorithm, SCG)来最大限度地散开种子节点。曹玖新等[6]提出了基于核数的启发式算法，该算法通过核数定义网络层次，层层剥去外层节点以获得内层的核心节点集合来解决影响力最大化问题。随后苏晓萍等[7]考虑网络中节点的结构特征利用结构洞思想[8]来评定网络中节点影响力，但文献[7]中提出的方法较适用于小型网络且并未将该思想进一步应用在影响力最大化问题中。Zhu等[9]提出基于结构的贪心(Structure-based Greedy, SG)算法通过选取能桥接多个群体的结构洞节点来扩大影响范围。

针对当前仅选取核心或边缘节点的算法造成影响范围小的现状，本文提出一种基于结构洞和度折扣的最大化算法(maximization algorithm based on Structure Hole and Degree Discount, SHDD)。该算法将结构洞思想和中心度思想互相融合应用到影响力最大化问题中,兼顾核心节点和结构洞节点在信息传播中的作用，提高最终的影响范围。

1 相关工作

1.1 传播模型

通常将社交网络表示成一个有向(无向)图G(V,E),V表示节点的集合，节点v∈V代表个人或组织；E表示边的集合，每条边(u,v)∈E表示节点u和节点v之间的影响关系。通常假设社会网络G(V,E)有n个节点、m条边，网络中的节点有两种可能状态：激活和未激活。未激活形式下的节点会受到已激活节点的影响，节点从未激活模式转化为激活模式的过程被称作激活。

目前影响力最大化问题中应用最广的传播模型是独立级联模型(Independent Cascade model, IC)和线性阈值模型(Linear Threshold model, LT)[10-11]。其中本文使用的独立级联模型是一个概率模型，节点u通过边(u,v)∈E激活节点v的概率为p(u,v)∈[0,1]。该模型下的传播方式如下：在t=0时刻，激活筛选出的种子节点集合S0，其他节点保持在未激活模式。St表示t时刻处于激活模式的所有节点的集合，则在t+1时刻利用St中的节点去激活其邻居节点，邻居节点被激活的概率是p(u,v)，并把所有被激活的节点添加到St中形成St+1。迭代操作这一过程直到不再出现新的节点被激活。尤为重要的是在此模型下，节点从未激活模式转换成激活模式的过程不可逆，并且节点v被节点u激活的概率p(u,v)是系统常量，而和其他试图激活节点v未遂的节点没有关系。

1.2 结构洞

把社交网络中的节点看作是村庄，则节点与节点之间的联系看作连接村庄的路。如果两个村庄没有直接连通的道路，需要通过第三个村庄才能连通两个村庄，则不能互相连通的两个村庄在结构上看存在空洞，称这个空洞为结构洞，而连接这个空洞的村庄被称为占据结构洞节点。如图1所示，若节点A、B、C、D两两互相连接则不存在结构洞；若节点A、B和C没有直接连接而是通过节点D建立的联系，如果去除节点D则节点A、B和C之间存在结构洞，而处于结构洞位置的节点D称作结构洞节点。

结构洞节点可以有效控制流向其邻居节点的信息，在信息传播方面，Lou等[12]发现在Twitter上，1%的结构洞节点决定着25%的信息流向，结构洞节点的加入可以扩大信息的扩散范围。例如在图2中，信息在网络中传播时假设无结构洞节点1的连接，信息的交互则仅限于单个团体中，若通过结构洞节点1，在A中接收信息后会以一定的概率p将信息传递到B中。

图1 结构洞概念图Fig. 1 Concept diagram of structure hole

图2 结构洞信息传播图Fig. 2 Propagation diagram of structure hole information

用网络约束系数CT(ConsTraint)和效率值EF(EFficient)[13]来作为结构洞节点评价标准，但是前者运行内存较大且随着网络节点数量的增加效果变差且不稳定，所以本文此次选用效率值EF来作为结构洞节点评价标准：

(1)

式中：EF(i)表示节点i的效率值；τ(i)代表直接与节点i相连的邻居节点的集合；j表示节点i的邻居节点；q代表节点i和j的共同邻居；ni表示节点i所处网络的大小；piq则如图3所示代表节点i连接q付出精力占总精力的比重;mjq代表节点j连接节点q付出的精力和节点j连接其他节点付出的最大精力的比值。piq的计算式如下：

其中:

mjq的计算式如下：

mjq=pjq/max(pjm);m∈τ(j)

权值相同的拓扑图节点j对于其邻居节点付出的精力相同,则有：

EiA=(1-1/2)/6=1/12,同理可得EiB、EiC、EiD、EiE、EiF分别为1/9、1/6、5/36、5/36、5/36，则EF(i)=7/9。

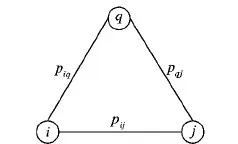
图3 评价节点i对节点q的投入精力Fig. 3 Investment evaluation of node i on node q

图4 效率值计算示意图Fig. 4 Schematic diagram of efficiency value calculation

2 基于结构洞和度折扣的最大化算法

2.1 影响力最大化现有算法

现有的影响力最大化算法中，DegreeDiscount算法在反映某些节点对当前领域的影响力方面有着良好的表现，基于选取结构洞节点的SG算法具有较好的扩散效果。

DegreeDiscount算法主要思想为：如果某个节点的邻居节点是种子节点时，则此节点的度在计算时应当打折扣，最终选取k个打折扣后度数仍最高的节点作为种子集合。如图5所示假定k=2，则根据DegreeDiscount算法会选取度数为7的5号节点和度数为6的3号节点，该算法只是考虑选取中心节点，其时间复杂度为O(klogn+m)。

SG算法的主要思想为：通过设定结构洞值找出社交网络中所有的结构洞节点，并通过贪心算法找出影响力值较大的k个结构洞节点作为种子集合。如图5所示假定k=2，则根据SG算法会选取结构洞值较高的2号和6号节点作为种子节点，该算法只选取了结构洞节点，其时间复杂度为O(kRn3)。

图5 DegreeDiscount及SG算法节点选择示意图Fig. 5 Schematic diagram of node selection for DegreeDiscount and SG algorithms

上述两种算法仅仅利用结构洞节点或核心节点无法使信息扩散得到最大化，结构洞节点可以看作网络中的边缘节点，只激活边缘节点或核心节点，在网络覆盖范围较大的情况下得不到理想的信息扩散范围。本文综合考虑社交网络中基于中心度的核心节点和结构洞节点的传播优势，利用结构洞理论可以弥补中心度理论不能识别桥接节点的问题，提出基于结构洞和度折扣的最大化算法(SHDD)。为了充分体现两个思想融合的优势，将二度邻居的影响添加到结构洞节点评价标准中来找出更好的结构洞节点。

2.2 SHDD

基于结构洞和度折扣的最大化算法(SHDD)的基本思想为：分两个步骤来挑选k个种子节点，首先添加k1个效率值最大的结构洞节点到种子节点集合中，其次添加k2个“度数最大”的节点到种子节点集合中。其中k1=|αk|，k2=k-k1。0<α<1 是一个关键值，这个值在后面的实验中给出。SHDD的伪代码如算法1所示。

算法1 SHDD。

输入 图G(V,E)，种子节点个数k,因子α；

输出 种子集合S。

1)

初始化S=∅,NS=∅,k1=「αk⎤，k2=k-k1，tv=0;

2)

for all nodev∈Vdo

3)

dv=d(v);

4)

SHv=EF(v);

//计算每个节点的效率值

5)

end for

6)

fori=1 tok1do

7)

8)

S=S∪{u};

9)

NS=NS∪N(u);

10)

end for

11)

fori=1 tok2do

12)

for all nodev∈VSdo

13)

for each nodem1,m1∈N(v)

14)

ifm1∈S

15)

tv=tv+1;

16)

end if

17)

end for

18)

ddv=dv-2tv-(dv-tv)×tv×p;

//度折扣计算

19)

tv=0;

20)

21)

S=S∪{m};

22)

end for

23)

end for

24)

returnS

算法1中：NS表示种子节点的邻居集合，N(u)代表节点u的邻居节点，tv指节点v的邻居是种子节点的个数，VS是去掉种子节点的节点集合。

算法第3)行：计算每个节点的度数并保存；第4)行：根据结构洞二度评价标准计算所有节点的效率值并保存，其具体计算方法将在2.3节中详细介绍；第6)～10)行：每次把效率值最大的节点添加到节点集合S中，并在下次选择的时候去掉种子节点和种子节点的邻居节点，以防止选择的结构洞节点过于集中，迭代选择出k1个节点添加到种子集合中；第11)～22)行是度折扣阶段：对种子节点的邻居节点进行度折扣计算，选出k2个ddv最大的节点到种子集合中。

假设社会网络G(V,E)有n个节点、m条边，SHDD的时间复杂度分析如下：第3)行的时间花费为O(m)；第4)行根据2.3节计算节点的效率值的时间花费为O(n)+O(m)；第6)～10)行选择结构洞节点的时间花费为O(k1n)；则第11)～22)行的度折扣阶段时间花费为O(k2logn+m)；因此算法的总时间复杂度为O(k2logn+m)。原基础算法DegreeDiscount时间复杂度为O(klogn+m)，因此SHDD没有增加额外的时间复杂度。

2.3 结构洞二度评价标准

式(1)的效率值仅仅考虑到节点及其一度邻居节点之间的结构特征，忽略了二度邻居的影响，会识别不出一些可能是结构洞的节点。如图6所示，根据式(1)可得节点E和F的效率值是：

EF(E)=EF(F)=(1-1/2×1)/2+

(1-1/2×1)/2=1/2

从一度邻居来看，节点E和F的拓扑结构相同，但是从二度邻居考虑，节点F有比E更好的拓扑关系。这种现象在式(1)的效率值的计算中无法体现，因此通过加入二度邻居来改进效率值的计算方法，更加精准地衡量结构洞节点。

在无向网络G(V,E)中，节点i的度记作：

其中:

(2)

式(2)考虑了节点对邻居投入的精力和对其二度邻居投入精力所占的比例，真实地反映节点的重要性。节点i的效率值为：

(3)

将式(2)代入式(3)得：

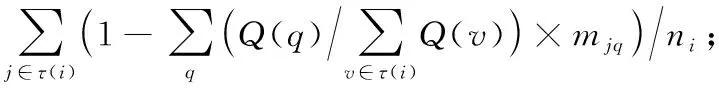
q≠i,j

节点E的效率值是：

mjq)/nE

q是节点E和j的共同邻居,则：

EF(E)=(1+18/34+19/34)/3=71/102

同理可得节点F的效率值：

EF(F)=(1+21/37+22/37)/3=80/111

图6 二度效率值计算示意图Fig. 6 Schematic diagram of second-degree efficiency value calculation

3 实验结果及分析

3.1 数据集

为验证本文提出的SHDD在IM问题上的可行性，本文选取Route Views、Net HEPT和Net PHY 3个数据集进行实验,数据集的相关属性如表1所示。

数据集1(Route Views)是互联网络的自治系统，点表示自治系统，边表示系统之间的通信,无向无权图，来自The Koblenz Network Collection(http://Konect.uni-koblenz.de)。数据集2(Net HEPT)是1991年至1993年的高能物理模块科学论文作者合作图，点表示作者，边表示两作者之间共同的出版物，无向无权图。数据集3(Net PHY)是物理学板块的论文作者合作图，点表示作者，边表示两作者之间共同的出版物，无向无权图。数据集2和3均来自论文共享网站arxiv(www.arxiv.org)。

表1 实验数据集Tab. 1 Experimental data sets

3.2 实验设置

本文实验对这3个真实网络数据集在IC传播模型中进行操作。为验证SHDD的性能，将选DegreeDiscount、SG算法和SH*DD算法与其进行实验对比。SH*DD算法基本与SHDD一致，唯一的区别是SH*DD算法利用1.2节中的结构洞评价标准来选取结构洞节点而SHDD是用2.3节中结构洞二度评价标准来选择结构洞节点。实验中SHDD的结果与α取值相关，SHDD的结果会随着α的变化而变化，因此需要设定不同的α值进行对比分析并找出最佳的α值。在传播概率不变且一致的IC模型下，为了方便对比分析，本文的算法在传播概率p=0.04的情况下进行。

在本文的对比实验中，4个算法的种子集合大小k∈{5,10,15,20,25,30,35,40,45,50}时进行对比分析。本次实验环境为：主频为2.50 GHz的Intel Core i5-2450,运行内存为6 GB。实验中涉及的编程语言采用python。

3.3 结果分析

在社交网络环境下，影响力最大化算法的评价指标为：1)影响范围，即筛选并激活相同规模的种子节点集合，在相同的传播模型下该集合最终激活的节点个数越多表示影响范围越广。本文是在IC传播模型下使用Monte-Carlo模拟2 000次传播过程并求取平均值作为影响范围。2)运行时间，即在相同条件下选择同等规模的种子节点集合所花费的时间t，t越小表明算法的效率越高。

3.3.1 SHDD结果分析

首先考察α的最佳取值，通过SHDD在3个数据集上对不同的α值时进行实验。

设置了在3个真实数据集中不同的α值(α∈{0.1,0.4,0.5,0.6,0.9})，随着不同的k值运行SHDD的影响范围如图7所示，图中影响范围代表影响节点数。从图7可以看出：在3个数据集中，当k值相同时，SHDD的影响范围随着α值的变化而变化。其中，在数据集1中，随着k值的变化，不同的α值的影响节点个数基本上都大于α=0.1时，当α取0.6时，SHDD的影响范围整体较大。在数据集2中，SHDD在α值取0.1和0.9时的影响范围整体最小，α的值越接近中心值影响范围越大。在数据集3中，随着k值的变化，SHDD在不同α值下的图像趋势和数据集2相差无几，α值取0.1和0.9时SHDD的影响范围整体最小，α的值越接近中心值影响范围越大。

通过图7的分析可知，在不同的数据集中SHDD的最优α值不同。而在不同的网络中，不可能对每一个α值进行模拟实验，然后选择最优α值。但从图7中可以看出，在3个不同规模的数据集中α=0.6时的SHDD的影响范围最为稳定，并且α=0.6是一个趋于中间的数值，不管数据集的规模偏大还是偏小，都不会呈现出影响效果偏差很大的现象。因此，本文把α=0.6作为算法的参数，后面实验中所提到的SHDD均是α=0.6时的SHDD。

3.3.2 对比算法结果分析

在3个真实数据集中，SHDD(α=0.6)、SH*DD算法(α=0.6)、DegreeDiscount和SG算法在传播概率为0.04的IC模型下的影响范围如图8所示。由图8(a)可知，在Route views数据集中，由于该数据集聚类系数较小属于稀疏网络，所以起桥梁作用的结构洞节点在信息传播中发挥着巨大作用，当k≤15 时，全部选取结构洞节点的SG算法其影响效果略优于SHDD，但只依靠结构洞节点并不能使信息在网络的中心位置进行更大范围的流通，所以随着k值的增大,SHDD综合结构洞节点和中心节点的传播优势,其影响范围超过了SG算法，而且SHDD的影响范围明显优于SH*DD和DegreeDiscount算法。在聚类系数较大的数据集2和3中，SHDD相比于其他算法有着较好的影响效果且随着k值的增大，SHDD的优势越明显。

图7 不同α值的SHDD在不同数据集上的影响范围Fig. 7 Influence range of SHDD algorithm with different α values on different data sets

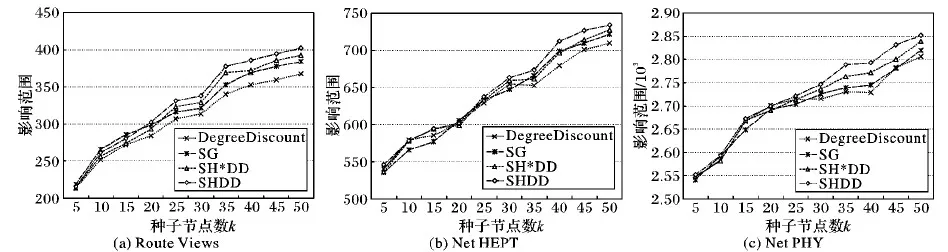
图8 不同算法在不同数据集上的影响范围对比Fig. 8 Influence range comparison of different algorithms on different data sets

不同算法在3个数据集上选取并激活50个种子节点的的运行时间如图9所示。从图9可以看出，各个算法的运行时间在同一数量级，其中，SG算法花费时间最多，DegreeDiscount、SH*DD和SHDD花费时间较为均衡。

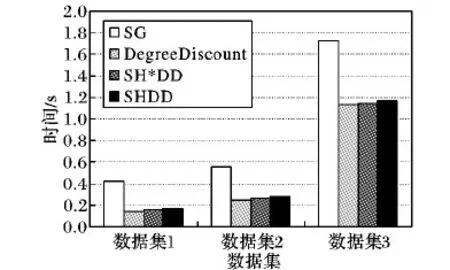
图9 不同算法在不同数据集上的运行时间对比Fig. 9 Runtime comparison of different algorithms on different data sets

通过综合分析图8～9可以得出以下结论：1) 与DegreeDiscount算法相比，SHDD在没有增加过多时间开销的同时提高了影响范围；与SG算法相比，SHDD降低了时间开销且在聚类系数较大的网络中扩大了影响范围，但在聚类系数较小的稀疏网络中SHDD在种子集合k较小的情况下影响范围稍微处于劣势，随着k值的增加SHDD影响范围超过了SG算法；2)在3个数据集中，SHDD的影响范围高于SH*DD算法，可反映出利用二度邻居选取结构洞节点的质量优于利用一度邻居选取的结构洞节点，不足之处在于增加了时间的消耗。

4 结语

本文分别研究中心度理论和结构洞理论的两种影响力最大化算法，在这两个算法特有的基础上提出基于结构洞和度折扣的最大化算法(SHDD)。本文方法相较于上述两种算法，主要有两处改进：1)将结构洞理论与中心度思想有效地结合；2)在大型社会网络中，考虑节点的结构特征将二度邻居的影响加入到结构洞检测思想中。实验表明，本文提出的SHDD在稳定运行时间的情况下提高了影响范围。未来我们将寻找更好的挖掘结构洞节点方法来提高算法的精度和效率，还可以考虑带有成本限制的影响力最大化问题[14]。