发掘隐性信息,开拓解题思维
2019-01-06仲惟超
仲惟超

【摘要】“四点共圆”因其隐蔽性被称为“隐圆”.在解决有关平面几何问题时,如若我们能够发现问题背景下的“隐圆”,便可借助圆的丰富性质解决问题,开拓我们的解题思维,突破解题难点.本文从“四点共圆”条件的探究出发,总结了发现图中“隐圆”的两条常用条件,并以典型题为例,阐述“隐圆”在解决较复杂的平面几何问题中的作用与优势,做到“图中无圆,心中有圆,解题有方,出奇制胜”.
【关键词】四点共圆;隐圆;平面几何;解题思维
初中数学图形与几何领域主要研究几何图形的边边关系、角角关系以及边角关系.而人教版义务教育教科书九年级上册“圆”这一章是义务教育阶段平面图形学习的最终章.在圆内,我们借助圆内有关性质,可以非常方便地进行角与角之间的相互转化,同时,本章数学活动2“探究四点共圆的条件”又引发了笔者的思考,如若将一些多边形问题放在圆的背景下解决,是否会突破解题难点,开拓解题思路呢?于是笔者进行了如下思考.
一、“四点共圆”条件探究
我们知道,根据圆的定义可知“到定点的距离等于定长的点在同一个圆上”.这也是我们研究“四点共圆”的理论基点,在此基础之上,我们可以思考以下问题:
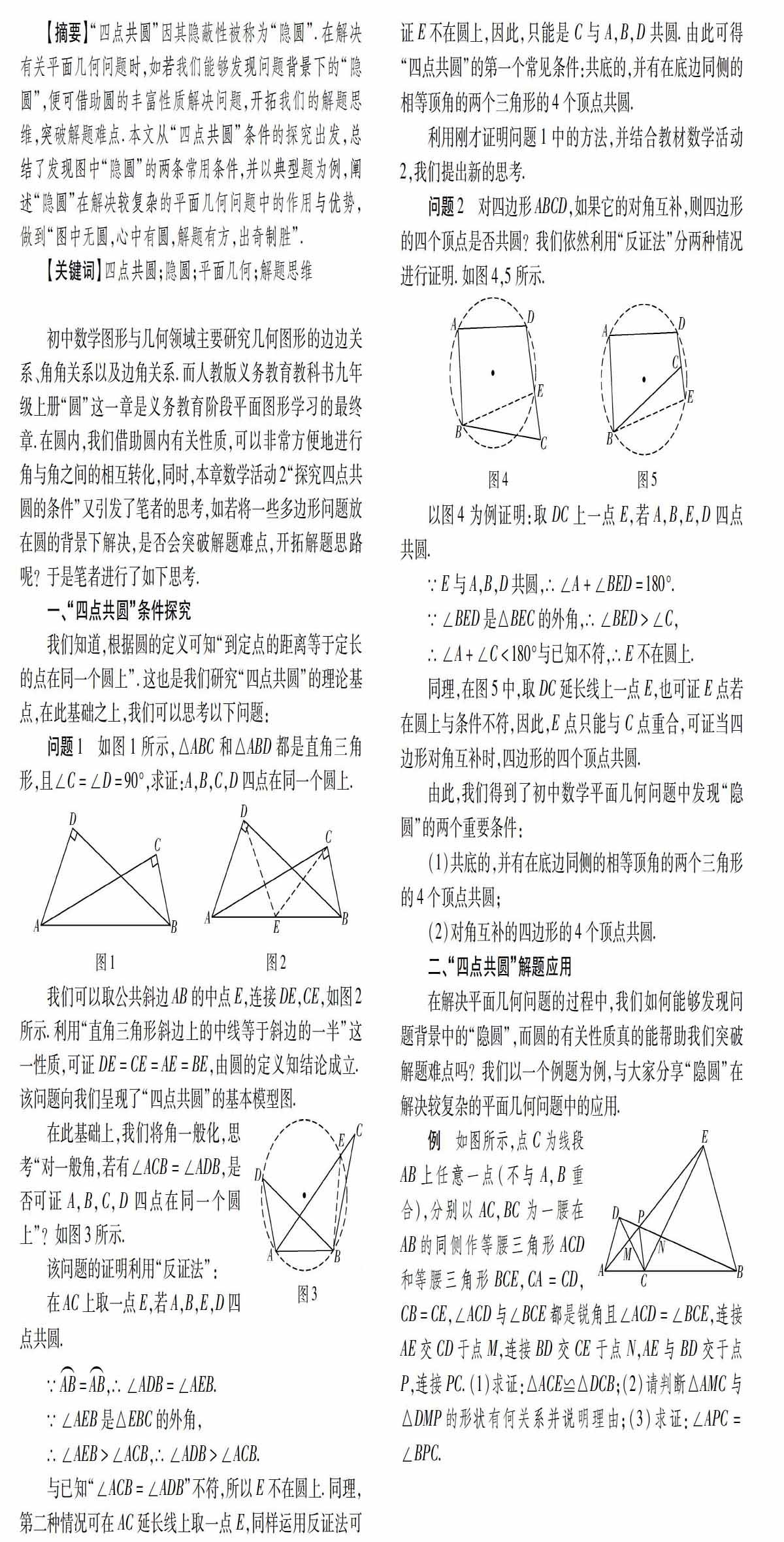
问题1 如图1所示,△ABC和△ABD都是直角三角形,且∠C=∠D=90°,求证:A,B,C,D四点在同一个圆上.
我们可以取公共斜边AB的中点E,连接DE,CE,如图2所示.利用“直角三角形斜边上的中线等于斜边的一半”这一性质,可证DE=CE=AE=BE,由圆的定义知结论成立.该问题向我们呈现了“四点共圆”的基本模型图.
在此基础上,我们将角一般化,思考“对一般角,若有∠ACB=∠ADB,是否可证A,B,C,D四点在同一个圆上”?如图3所示.
该问题的证明利用“反证法”:
与已知“∠ACB=∠ADB”不符,所以E不在圆上.同理,第二种情况可在AC延长线上取一点E,同样运用反证法可证E不在圆上,因此,只能是C与A,B,D共圆.由此可得“四点共圆”的第一个常见条件:共底的,并有在底边同侧的相等顶角的两个三角形的4个顶点共圆.
利用刚才证明问题1中的方法,并结合教材数学活动2,我们提出新的思考.
问题2 对四边形ABCD,如果它的对角互补,则四边形的四个顶点是否共圆?我们依然利用“反证法”分两种情况进行证明.如图4,5所示.
同理,在图5中,取DC延长线上一点E,也可证E点若在圆上与条件不符,因此,E点只能与C点重合,可证当四边形对角互补时,四边形的四个顶点共圆.
由此,我们得到了初中数学平面几何问题中发现“隐圆”的两个重要条件:
(1)共底的,并有在底边同侧的相等顶角的两个三角形的4个顶点共圆;
(2)对角互补的四边形的4个顶点共圆.
二、“四点共圆”解题应用
在解决平面几何问题的过程中,我们如何能够发现问题背景中的“隐圆”,而圆的有关性质真的能帮助我们突破解题难点吗?我们以一个例题为例,与大家分享“隐圆”在解决较复杂的平面几何问题中的应用.
该解题思路的难度在于学生习惯运用角的转化证两角相等,而非通过证角平分线得两角相等,因此,学生无法想到通过添加此辅助线进行构图;其次对三角形全等性质的运用往往停留在对应边相等,对应角相等,而非面积相等等,这些思维的局限性导致该问题无法解答.
如果学生能够从该问题背景下找到图形中的“隐圆”,该问题的思维难度将降低不少.如图所示,在共底的△DPC与△APC中,我们已知底边PC的同側顶角∠BDC=∠EAC,则A,C,P,D四点共圆.
此种解题思路正是学生习惯使用的利用角的转化证两角相等,符合学生的思维习惯,降低了思维难度.其中的解题核心就是发现图中的“隐圆”,并利用圆的相关性质进行角的转化.
以该题为模型,下面这道变式题也就好想多了:
变式 以△ABC的边AB,AC为边,分别向外作正三角形ABD、正三角形ACE,DC,BE交于点F.求∠DFE的度数.
在解决该问题时,我们可以通过添加辅助线,连接AF,构造共圆的四点A,F,C,E(如图所示).
根据题中条件易得△ACD≌△AEB,
可见,发掘问题背景下的“隐圆”信息对解决较复杂平面几何问题的重要性.
