一台大载荷比Φ32 mm六分量天平的研制

崔智强,李 勇,王世红,赵长辉

(中国航空工业空气动力研究院,辽宁 沈阳 110034)

隐身巡航导弹[1-2]以其难探测、难防御的特点被世界各国所重视,研制该种导弹就需要进行风洞试验。根据隐身巡航导弹气动布局特点来研制与其载荷相匹配的测力天平[3-4],是保证试验精准的关键。隐身巡航导弹一般为大展弦比、长机身构型,气动上具有高升阻比的特点;同时,相对扁平的弹身和V形尾舵,决定了低侧向力的气动特性,即气动载荷上是较大的升阻比和较大的升侧比。常规风洞测力天平阻力、侧力及偏航力矩量程远大于隐身布局导弹模型的实际气动载荷,用大量程的天平去测量很小的气动力,无疑会引起阻力、侧力和偏航力矩较大的测量误差。因此,有必要根据隐身巡航导弹模型的气动载荷特点,设计出具有较高阻力、侧力、偏航力矩测量精准度的专用天平。

1 天平设计载荷及直径的选取

根据某隐身巡航导弹模型外形,采用CFD计算方法进行气动力的载荷估算,并选取天平的设计载荷,见表1。表中,Fx为阻力,Fy为升力,Fz为侧力,Mx为滚转力矩,My为偏航力矩,Mz为俯仰力矩。根据模型使用情况选取天平直径32 mm。

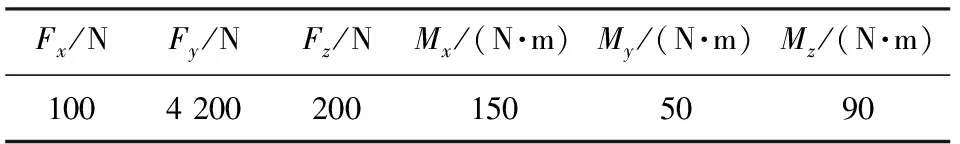
表1 天平设计载荷

2 天平设计的主要技术难点

由天平的设计载荷可以知道该天平的纵、横向载荷比为21∶1,而常规的杆式天平该比一般在2∶1～5∶1之间。因此在保证天平横向测量元件的纵向刚度的同时,提高天平横向载荷测量的灵敏度是天平设计的一大难点。

由天平的设计载荷可以知道该天平的升阻比为42∶1,而常规的杆式天平该比一般在15∶1～20∶1之间。因此在保证天平阻力测量元件纵向刚度的同时,提高天平阻力测量的灵敏度是天平设计的又一难点。

3 天平结构方案研究与选取

目前常规使用天平的总体结构为并联结构,前后柱梁结构组合测量天平除阻力之外的其他分量,采用“T”型梁为阻力元件结构,测量天平阻力,如图1所示。由于此种结构天平组合程度过高,对于大载荷比的设计条件,很难同时得到所有分量的满意设计输出。根据本次设计背景知道,本天平设计的阻力与侧力测量量值较小,载荷不匹配比较严重,这是设计考虑的主要问题。因此,采用小量独立分离设计方案是本次设计的主要指导思想。阻力测量元件在并联结构天平上是独立的结构,可以采用力放大的方法解决阻力小量设计输出问题。而侧力测量元件在并联结构天平上是与其他元件共用的结构,因此需要采用独立分离出来的结构设计方法来解决侧力小量设计输出问题。

3.1 侧力测量结构

根据设计载荷的特点,侧力测量量值较小,达到较大的灵敏度且与偏航力矩进行组合测量的难度比较大,故本方案选择独立分离元件结构进行测量。借鉴经典杆式天平的“1”字阻力元件结构,采用多片的薄片梁结构进行支撑,“1”字敏感元件进行侧力感应,此种结构特点是仅对侧力比较敏感,对其他载荷的承载能力较强。本方案选取20片厚0.7 mm的支撑梁进行支撑,用敏感元件为厚2 mm、高6 mm的矩形梁进行感应测量。

动求解方程的系数和程序,见图7。最终六连杆并联复位机构满足了复位指标角的精度±3″和线位移精度±0.03 mm的要求。

3.2 阻力测量结构

阻力是测量量中的最小量,要实现阻力的测量,同样需要解决阻力元件结构对其他载荷的承担及阻力敏感元件的测量灵敏度问题。阻力元件支撑问题的解决是通过增加支撑梁数量、减薄支撑量厚度的方法来实现。此种支撑结构可实现阻力元件对其他载荷支撑的同时使测量量损失最小。本方案选取的支撑量数目20片,厚、长、高分别为0.6 mm、7.5 mm、9 mm。提高测量敏感元件灵敏度的方法是借鉴经典杆式天平的“π”型阻力元件结构。利用该结构的力的放大功能,增加元件的偏心距离,来获得元件测量部位的较大的弯矩,从而得到较大的灵敏度输出,本方案的偏心距选取6 mm,设计中可根据实际情况继续增加偏心距离,达到增加灵敏度输出的目的。

3.3 其他力的测量结构

主要的不匹配量解决后,其他的测量分量采用阻力元件结构前后的2个矩形梁元件进行测量,通过调整矩形梁的长宽比及前后矩形梁的距离,很容易得到4个力的较理想的灵敏度输出。

3.4 天平结构图

根据本项目测量载荷特点研制的天平结构如图2所示。图中,阻力与侧力测量元件为单独的元件结构，其余元件为组合元件结构。

4 天平设计应变计算

采用材料力学经验公式对天平各测量元件尺寸进行调整及优化后,采用有限元法进行验证计算。两者计算结果比较详见表2。表中,εFx,εFy,εFz分别为阻力、升力和侧力作用下产生的应变;εMx,εMy,εMz分别为滚转力矩、偏航力矩和俯仰力矩作用下的应变。天平各元设计应变在1.5×10-4～7×10-4之间,满足风洞应变天平的设计规范要求,天平设计应变云纹图见图3～图8。

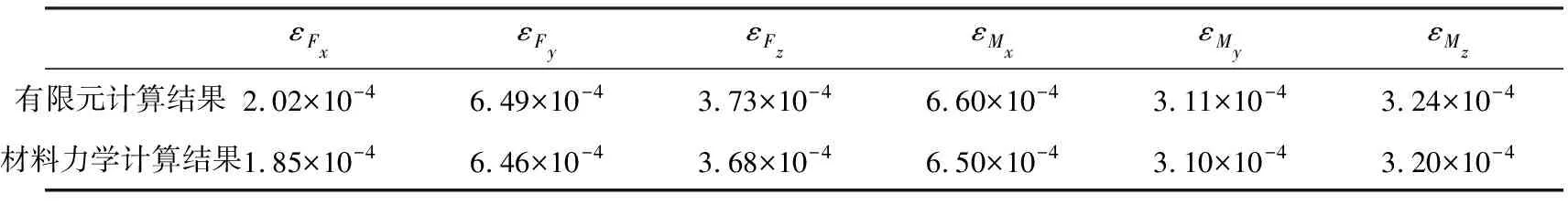
εFxεFyεFzεMxεMyεMz有限元计算结果2.02×10-46.49×10-43.73×10-46.60×10-43.11×10-43.24×10-4材料力学计算结果1.85×10-46.46×10-43.68×10-46.50×10-43.10×10-43.20×10-4

5 天平加工和粘贴

该天平的加工主要采用电火花与线切割等工艺加工。由于天平载荷不匹配情况比较严重,大量对小量的干扰将是校准中的主要难题,通过天平系数矩阵的修正无法完全消除。因此,物理结构上减小干扰也是得到较高校准准度的必要措施。该天平的前、后锥及阻力、侧力元件的各梁的形位公差都有更为严格的要求,均小于0.01 mm。

天平粘贴选用高精度金属应变计,组桥采用惠氏顿全桥法,同时在桥路中串联温度敏感电阻对温度影响的零点漂移进行补偿调节[5],以达到天平零点温度影响最小。

6 天平校准

天平校准标定的方案及过程对天平测量精、准度具有很大的影响[6-7]。由于本天平载荷比较大,天平安装姿态角度误差带来的大载荷量对小载荷量的干扰会较大。因此,天平校准中对于天平的安装姿态进行了严格的控制,采用激光跟踪仪进行加载头初始定位的角度位置测量,角度误差为30″,线性误差为0.05 mm。校准采用全自动激光测量反馈的体轴天平校准系统,复位精度可达4″,有效保证了天平校准整个过程的姿态位置准确。天平校准准度达到使用要求,详见表3。表中,Δ表示绝对误差,δ为相对误差,3δ为极限误差。天平温度灵敏度影响修正[8]是通过20 ℃与60 ℃ 2种状态对天平进行加载得到温度影响系数,进而在试验中对其进行修正。

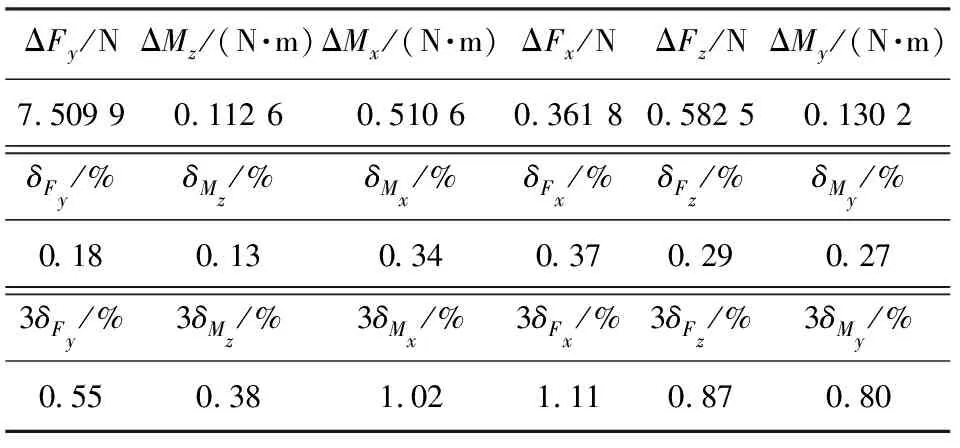
表3 天平校准准度指标

7 天平动校风洞实验

试验模型采用某隐身巡航弹模型,以Ma=0.8时试验重复性的形式给出天平动校结果。试验结果表明本天平精度优于常规天平,接近先进指标范围。天平试验精度详见表4。表中,α为实验攻角;σMx,σMy,σMz分别为滚转力矩、偏航力矩和俯仰力矩的5次均方差;σFx,σFy,σFz分别为阻力、升力和侧力的5次均方差。

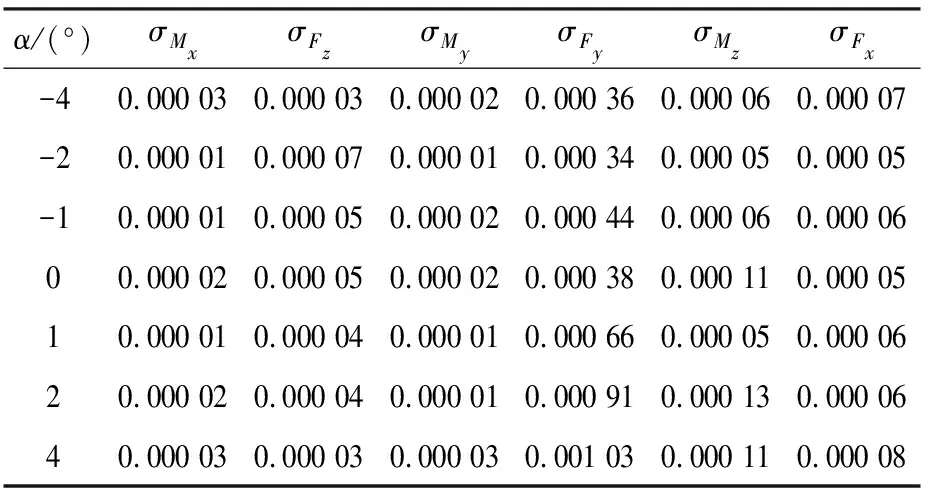
表4 天平试验精度

8 结束语

大载荷比Φ32 mm六分量天平设计是成功的。天平性能稳定,动校精度达到了国军标的先进水平。目前该天平已成功地应用到型号实验之中。

大载荷比Φ32 mm六分量天平总体结构布置比较合理,各元件的尺寸设计得当,在具有较好刚度的同时达到小阻力、小侧力的小量载荷精确测量的目的。

大载荷比Φ32 mm六分量天平研制的成功,为类似隐身巡航导弹气动布局模型测力天平的研制及载荷极不匹配测力天平的研制提供了借鉴。