EPR信道保真度的研究

张安琪，李 晖

（沈阳工业大学信息科学与工程学院,沈阳110870）

1 引言

量子隐形传态方案[1]是基于纠缠对实现的通信过程。近几十年，从最简单的EPR纠缠对[2]开始,研究人员已经提出诸多可行的量子隐形传态方案[3-4]。但是受工业制造和环境噪声等方面的影响，量子隐形传态不能保证实现信息100%的“复制”，所以为了衡量量子隐形传态方案是否成功，研究人员提出了一个量子通信中的重要物理量——保真度[5-6]。由于量子隐形传态的理想的量子信道是不存在的，学者们致力于用不同方式来提高信道保真度以达到正确传送量子信息的目的[7-9]。文献[10]分析了以非最大纠缠的EPR态和GHZ态为信道的保真度，其中用信道系数代表纠缠度，验证了保真度不但与信道纠缠度相关，还与待传送粒子的纠缠度有关。文献[11]提出一种测量保真度的方法，为理论计算建立保真度数学模型奠定了基础。康永香，夏云杰等人在特定系统中通过提高信道的纠缠度，以及在传输过程中进行纠缠态提纯来提高保真度[12-14]。文献[15]描述一个优化且为纯量子的贝叶斯推理修正保真度的状态过程，可以求得保真度的极大值和极小值，但是没有解释保真度在两极值之间的变化规律。文献[16、17]研究了不同类型噪声环境下的信道保真度，提出不同的噪声对保真度的影响不同，给出了粒子纠缠态通过噪声量子信道的最佳保真度，并证明了量子通信比经典通信更具优势。可见，在量子通信中，针对不同类型的噪声，可以设计不同信道系数幅度比的信道以提高保真度。

基于以上内容，当以EPR为信道传送粒子时，由于通信信道受到不良影响，信道纠缠度不能达到理论上的最大值，保真度将随着传送的粒子数的增加而减小。但是，使用量子隐形传态方案传送信息时，不可能每次只传送一个粒子，因为这样会造成时间成本极大的浪费。所以本研究以非最大纠缠度的EPR为信道传送（n=1、2、3）粒子，在信道的基础设计方面，讨论随着传送粒子数的增多，保真度与信道系数幅度比之间的变化情况。根据研究结果，可以得出量子隐形传态为满足保真度大于0.6700的临界值，需要对EPR信道系数幅度比的取值条件，便于应用在实际的信道设计中。

2 量子隐形传态信道保真度模型

设n粒子未知量子态从发送者Alice传送给接收者Bob。n粒子未知量子态为：

传送n粒子未知量子态的EPR信道表示为：

式中，Xi、Yi为信道系数，其幅度满足对信道系数幅度满足表示第i对EPR信道；下角标Ci1、Ci2分别表示组成第i个信道的纠缠粒子对中的第1个粒子和第2个粒子。

将每个EPR信道的第一个粒子Ci1发送给Alice，第二个粒子Ci2发送给Bob。Alice手中共有2n个粒子（n个被传送粒子和n个信道粒子Ci1），Bob手中有n个信道粒子Ci2。

Alice拥有的总的量子系统表示为：

然后，Alice需要对手中的粒子进行Bell测量。

经过Bell测量后总的量子态由式(4)变为：

其中，Pj表示Bell测量的测量结果是的共轭转置，Tr是求迹过程。

Bell测量后，Bob手中的粒子发生坍缩，Alice通过经典信道告知Bob自己Bell测量的结果，则此时Bob手中粒子的量子态密度矩阵可以表示为：

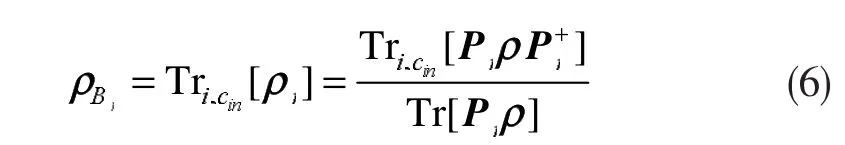
然后，Bob根据Bell测量结果设计合适的幺正算子U作用在总的量子态上，得出的最终量子态密度矩阵就是Alice需要传送的量子态的密度矩阵，表示为：

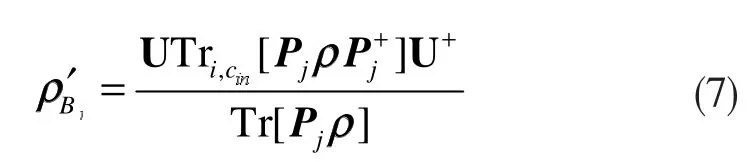
式中，U+是U的共轭转置。

将式(7)带入保真度的数学模型为：

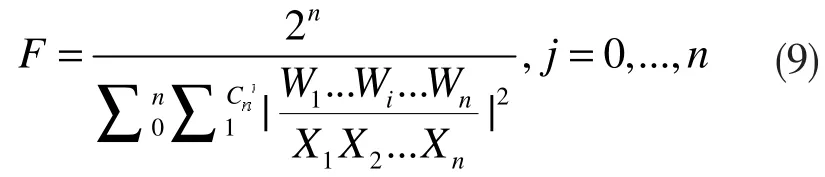
在式(9)中可以看到，分母的每一项都对信道系数进行平方处理，相当于取信道系数的幅度，令 k=，定义为以EPR为信道时的信道系数幅度比，当EPR信道为最大纠缠时有，若EPR纠缠度为非最大纠缠时，则k＞1。进一步化简，式(9)可以写成：

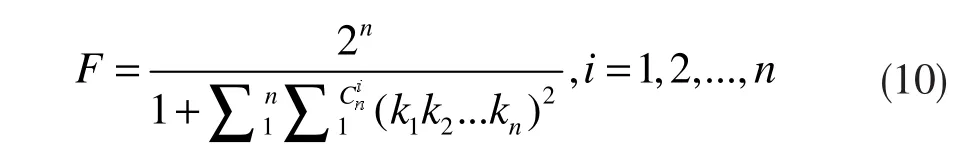
式(10)将信道系数幅度比ki与保真度F联系了起来，可以研究保真度随信道系数幅度比之间的变化情况及不同信道系数幅度比之间相互影响的情况。由式(10)可得，当信道为最大纠缠度即k1=k2=...=ki=...=kn=1时，保真度达到最大值，即F=1。

3 以EPR为信道传输3粒子的实现

假设发送者Alice有一个三粒子量子态，由粒子1、粒子2和粒子3构成，可表示为下式：

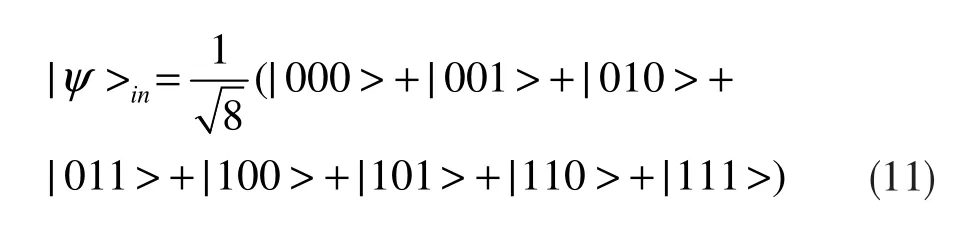
传送三粒子的EPR信道分别由粒子C11和粒子C12，粒子 C21和粒子 C22，以及粒子 C31和粒子 C32组成，且信道系数幅度满足

所以，发送者Alice手中有粒子1、粒子2、粒子3、粒子C11、粒子C21和粒子C31。发送者Alice总的量子系统表示为：

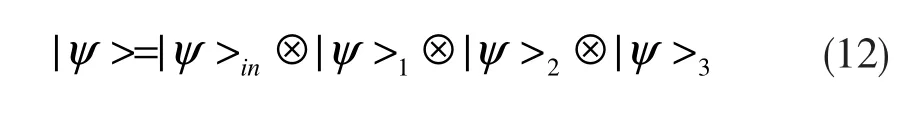
Bob手中有粒子C12、粒子C22和粒子C32。然后，Alice对手中的粒子1和粒子C11，粒子2和粒子C21，粒子3和粒子C31分别进行Bell测量。

Bell测量结束后，Bob手中的粒子坍缩为：

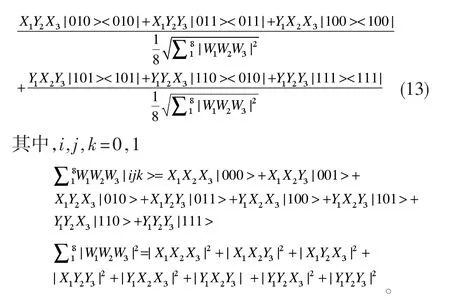
式(13)经过幺正变换后量子态的密度矩阵为：

中国特色社会主义制度自信与国家自信的关系最为紧密。新中国成立时，确立的是新民主主义制度，当时的中国仍是一个新民主主义国家。1956年，社会主义改造的完成和社会主义制度的基本建成，标志着中国从新民主主义社会过渡到了社会主义社会。在“四个自信”中，文化自信、道路自信和理论自信的历史起点都先于新中国的成立，只有制度自信的历史起点与新中国的成立是同步的。在现代意义上，建立一个国家，必然要相应地建立一套制度体系，离开一定的制度体系，国家是无法存在。所以在“四个自信”中，制度自信与国家自信的关系最为紧密。

可以验证，该信道在单位时间内传送了三个粒子，当k1=k2=k3=1时，保真度最大，即F=1。这表明这种演化推导保真度的方式是正确的。

4 实验仿真与数据分析

在上述理论分析的基础上，对保真度变化与纠缠信道系数取值之间的关系进行定量分析。分别定量分析了一对EPR信道传送单粒子的保真度、两对EPR信道传送2粒子的保真度以及三对EPR信道传送3粒子的保真度变化，及其纠缠信道系数幅度比的取值。以经典信道所能达到的最大保真度0.6700为临界值，当保真度大于0.6700时，认为量子隐形传输成功。当保真度减小到临界值以下，则界定量子隐形传输失败。

数据分析共分为三个部分：首先给出了保真度随信道系数幅度比的变化情况；然后给出保真度为临界值时，多对EPR信道系数幅度比之间的变化关系；最后研究信道系数幅度比之和随着信道系数幅度比的变化规律。

图1和图2分别为一对和两对EPR传输粒子时保真度随信道系数幅度比变化的曲线图。图中水平实直线为临界值0.6700。

图1 一对EPR信道k1-F变化曲线

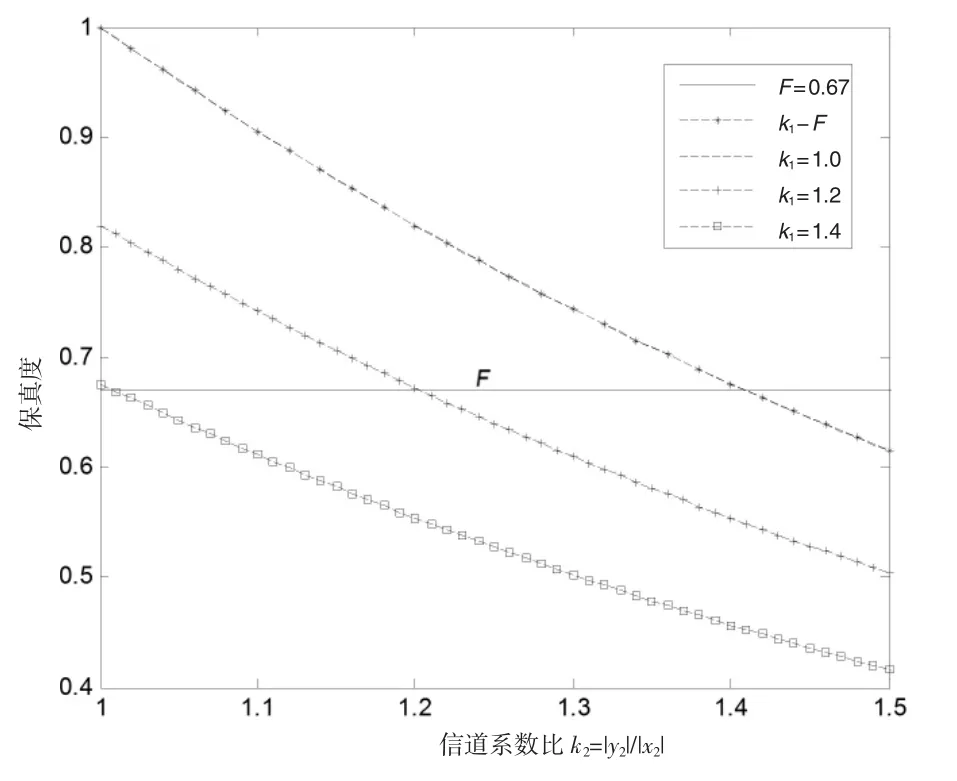
图2 两对EPR信道k2-F变化曲线

如图1所示，在k1-F曲线中，信道的保真度从1.0000开始随着信道系数幅度比k1的增大而快速减小，至k1=2.6000，保真度为0.2577处，保真度随着k1的增大而缓慢减小，并逐渐趋近于0。保真度F=0.6700所对应的k1值为1.4089。当F＞0.6700，即信息正确传送时，信道系数幅度比的取值范围k1∈(1，1.4089)。

图2表示当其中一对EPR信道k1增加时，k2-F曲线会随着k1的增加而下降,表明正确传送量子信息的k2范围缩小，使信道设计更加困难。k1=1的曲线和k1-F重合，说明两对EPR信道当中有一对信道系数幅度比为1时，保真度只与另一对信道系数幅度比相关，相当于一对EPR信道的保真度。这也表明最大纠缠态的EPR信道是最理想的信道，当多对EPR为信道传送粒子时，最大纠缠态的EPR信道对于总信道的保真度无影响。三条k2-F曲线起始坐标分别为(1.0000,1.0000)、(1.0000,0.8197)、(1.0000,0.6757)，它们的纵坐标差值是递减的，即曲线向下移动的程度变小，这说明信道系数幅度比增大对保真度的影响程度减小。当k1=1.4089时，其k2-F曲线的起始点坐标为（1.0000,0.6700），所以在 k1＞1.4089时，无论k2取何值，其k2-F曲线上每个点均在F=0.6700临界值以下，无论信道如何设计，量子信息均无法正确传送。

图3、图4、图5、图6及图7探究多对EPR信道传输粒子时，各个信道的信道系数幅度比之间的相互关系。为了便于对信道系数幅度比规律的探究，以下探究均是在保真度为临界值的条件下完成的，即F=0.6700。

图3中点横线上的点均可使F=0.6700，表示两对EPR信道的信道系数幅度比k1和k2之间的相互关系是非线性的。该曲线与X、Y轴分别交于点(1.0000,1.4089)和点(1.4089,1.0000)；在曲线上任意取得一点(1.1000,1.3044)，该点的坐标X、Y轴相互交换后的坐标(1.3044,1.1000)和点(1.2014,1.2014)都在该曲线上，这证明该曲线凹向原点 (1.0000,1.0000)且关于直线X=Y对称。在由曲线与X、Y轴相交所围成的区域内取得的点（k1,k2）可使F＞0.6700，保证量子信息的正确传送。

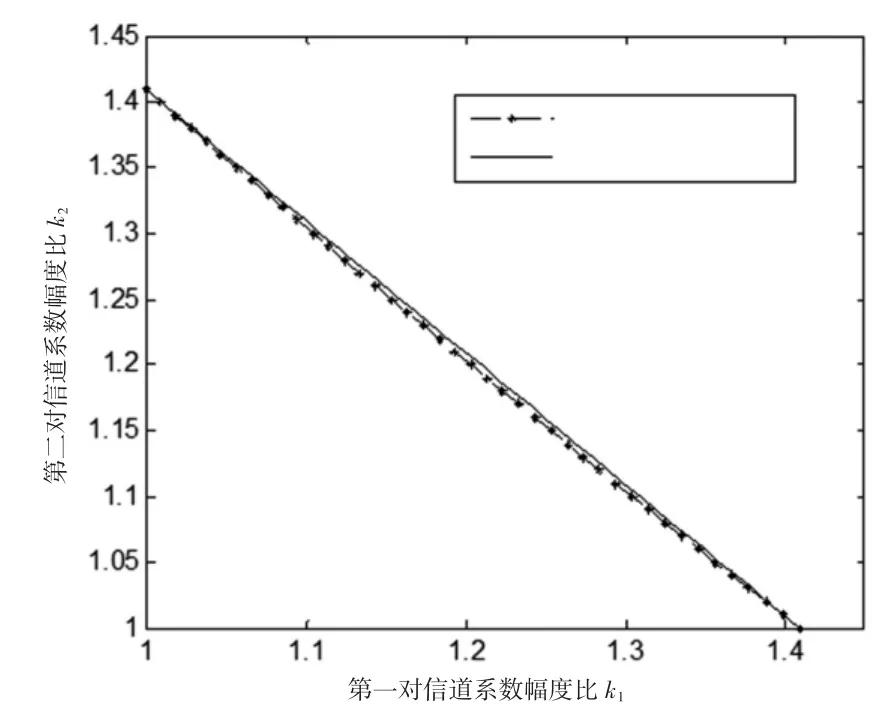
图3 两对EPR信道k1、k2关系曲线

图4中的点可以满足F=0.6700，即表示三对EPR信道系数幅度比k1、k2和k2之间的关系。图中由点表示的面构成一个顶点坐标分别是（1.4089,1.0000,1.0000）、（1.0000,1.4089,1.0000）、（1.0000,1.0000,1.4089）的曲面。在曲面与三个坐标轴相交形成的平面所围成的密闭体区间内F＞0.6700，可以确保量子信息的正确传送。

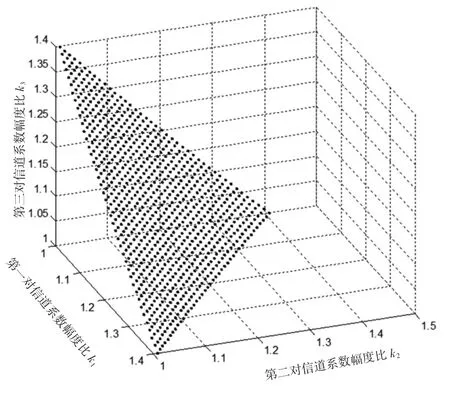
图4 三对EPR信道k1、k2和k3关系曲线

图5、图6和图7研究信道系数幅度比之和S随信道系数幅度比ki变化的曲线。

在图5中，由于k1-S曲线和k2-S曲线重合，这表明在以EPR为信道的量子隐形传送过程中，每对EPR的信道系数幅度比k1和k2对于整体信道的影响是相同的。在该图像中，每条ki-S曲线的最低点坐标为（1.2014,2.4028），最高点坐标为（1,2.4089）和（1.4089,2.4089）。

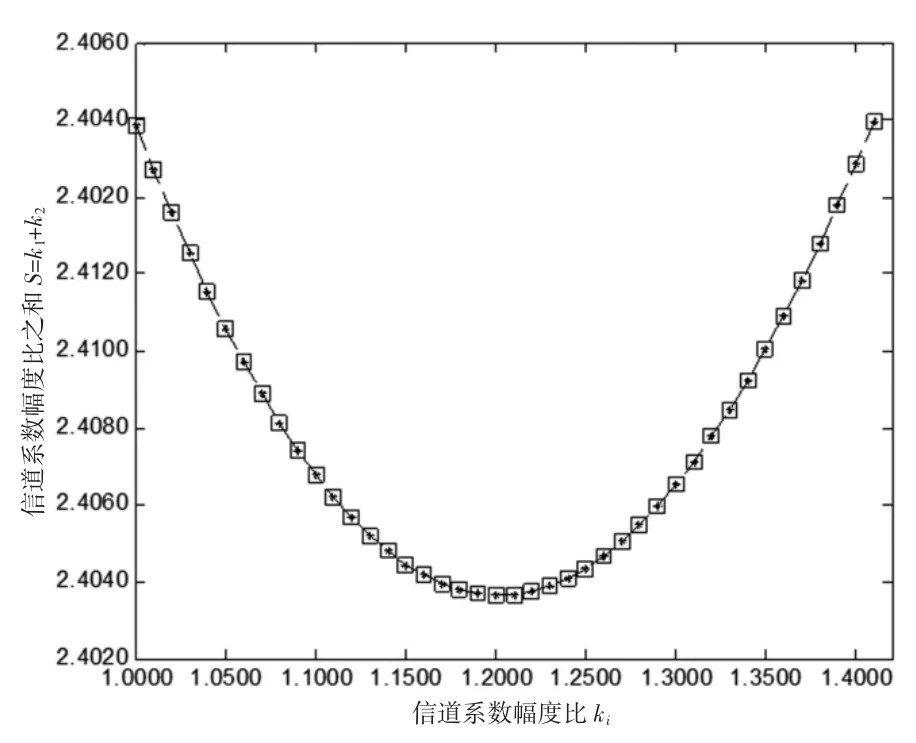
图5 两对EPR信道S随ki变化曲线

由于k1-S曲线和k2-S曲线是重合的，取k1-S曲线研究单独一对EPR信道系数幅度比的性质。取k1-S曲线在定义域（1.2014,1.4089）内的曲线图像以k1=1.2014为对称轴反转，形成“—□—”图线，如图6所示，在定义域（1.0000,1.2014）内，“—□—”线和“—*—”线完全重合，说明k1-S曲线是关于k1=1.2014对称轴对称的曲线。

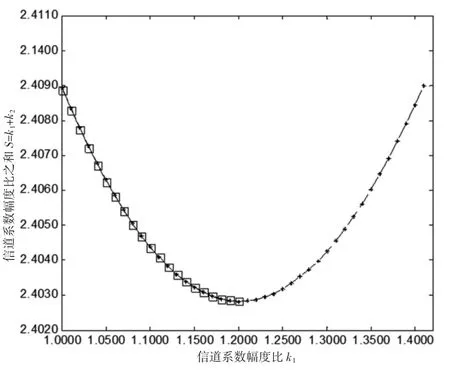
图6 两对EPR信道S随k1变化曲线

为了说明ki-S曲线的意义，在k1-S曲线上任取一点（1.1000,2.4044）为例进行解释。点（1.1000,2.4044）代表的意义是：在用两对EPR传送信息的量子信道中，当k1=1.1000，k1=S-k1=2.4044-1.1000=1.3044时，能保证信道保真度F=0.6700，k1-S曲线的其余点同理。所以在k1-S曲线上，点（1.1000,2.4044）到点（1.1000,2.0000）直线范围之间的点表示的是：当k1=1.1000时，k2在1.0000～1.3044区间内的任意取值都能保证信道保真度F≥0.6700，即量子信息能够正确传送。所以曲线上每个点到直线S=2.0000的距离可以间接表示在该点条件下量子信息正确传送的信道系数幅度比取值的范围。综合来看，在ki-S曲线上，最高点坐标的信道系数幅度比之间的差值为0.4089，最低点坐标的信道系数幅度比之间的差值为0.2014，所以信道系数幅度比的差值越小，使量子信息能够正确传送的信道系数幅度比的取值范围也就越小。以上分析表明以二对EPR为信道时，信道系数幅度比ki在从1.0000变化到1.4089的过程中，能正确传送量子信息的信道系数幅度比的取值范围先减小后增大，当ki=1.2014时，能正确传送量子信息的信道系数幅度比的取值范围最小。

如图7所示，曲面上的每一点都能满足信道保真度F=0.6700。曲面上最低点和三个最高点分别代表当满足信道保真度F=0.6700时的k1、k2及S的值。

还可进一步求得相应的k3值，如表1所示。

在图7曲面上每一点到平面S=3.0000的直线区间内取得的点（k1,k2,S）均可使F≥0.67，保证量子信息的正确传送。在曲面的最低点，任意两个信道系数幅度比之差取绝对值，三个绝对值求总和为0；同理，在最高点，三个总和值都为0.8178。类似于上述分析的以两对EPR为信道的ki-S曲线，随着任意两个信道系数幅度比之差取绝对值求和值的减小，能正确传送量子信息的信道系数幅度比的取值范围减小，曲面最低点，有k1=k2=k3=1.1338时，能正确传送量子信息的信道系数幅度比的取值范围最小。

图7 三对EPR信道S随k1、k2变化曲面

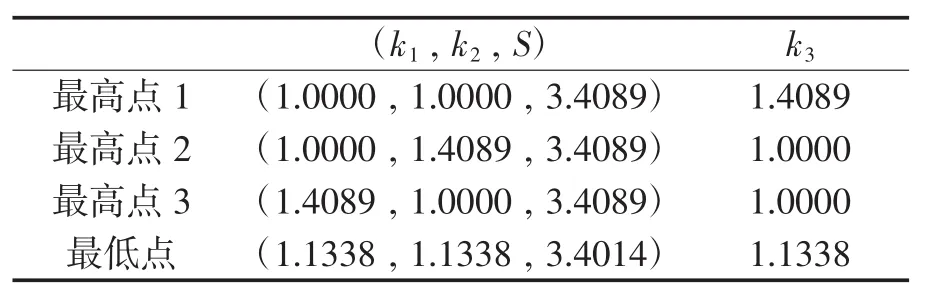
表1 图7的最高/最低点坐标及对应k3值

5 结束语

对以EPR为信道传送粒子信道模型的保真度与信道系数幅度比之间的关系规律进行了探讨。验证了当分别以一对，二对和三对EPR为信道传送粒子时，k-F曲线会怎样随k的变化而变化的规律。当两对以上的EPR为信道时，理论上，每对EPR对于总信道的影响是相同。以此，可推广得知以n对EPR为信道传送多粒子时，每对EPR在总信道中均处于对称的地位，对总信道的影响相同，但为了保证量子信息的正确传送，总信道的信道系数幅度比之和S在信道设计方面要满足一定的取值条件才能保证传输成功。对信道系数幅度比之和的范围的研究结论，对于在工程中展开信道设计具有直接的应用价值。