路灯监控系统中时序数据流的异常值检测研究*

黄雄波，钟 全

（1.佛山职业技术学院电子信息学院，佛山528000；2.广州市明锐电气技术有限公司研发部，广州510800）

1 引言

随着社会的不断进步和科学技术的高速发展，城市景观照明系统已成为城市建设的一项重要内容。此系统融合了通信技术、电气技术，检测技术、控制技术，采用移动无线网络，由上位机管理软件、信号中继器、Internet互联网络、移动通信网络、执行终端构成，对城市景观照明系统的设备进行实时监控，是保证系统安全可靠运行的重要手段。在实际应用中，通常需要对大量的灯具、继电器和接触器的实时状况进行信息采集和监控。

对设备进行实时监控导致了海量时序数据流的产生。以10s的时间间隔采集灯具的电流、电压、温度及光照度等物理参数，则10万盏灯具每天约产生100MB的时序数据流。为了能对这些历史时序数据流进行永久性的储存，一些高效的有损压缩算法被提出来。卢秉亮等基于旋转门压缩算法，将数据流注册到区域字典中并进行比例压缩，从而设计实现了一种高速的数据流压缩/解压缩算法[1]；张冬冬等通过对历史时序数据流实施多层递阶抽样存储，并在内存中建立有关聚集值的 HDS-Tree索引，实现了对无限数据流历史数据的存储管理[2]；冯秀兰等采用加权最小二乘法对时序数据流进行分段曲线拟合，并对拟合结果进行聚类分析，进而得到了一种高保真的数据流在线压缩存储方法[3]。

注意到路灯时序数据流往往呈现出在某一均值上作微弱随机波动的特点，据此，我们可以放弃对海量历史数据流的存储，转为对时序数据流的异常值进行检测和记录，以便实现对系统中各元件进行故障检测和预警分析。

2 问题描述

路灯时序数据流的观测值有时因受异常事件、设备故障、干扰或误差的影响，会出现与大多数观测值不一致的情况。通常把这些偏离正常数值的观测值称为异常值。异常值在时序数据流中属于少数，但却有着重要的应用价值。

时序数据流的异常值通常分为两种[4-5]——附加异常值（Additive Outlier Value,AOV）和新息异常值（Innovation Outlier Value,IOV）。其中，AOV仅作用于当前时刻的序列，而IOV则以冲击函数的激励形式影响着随后的序列观测值。令Yt 为没有异常值发生的时序数据流，wt 为Yt 叠加异常值后的时序数据流，对Yt进行去趋势和去周期的处理后，所得到的近似平稳序列Yt便可由自回归模型 (Autoregressive Model,AR)来描述。于是，当时序数据流在时刻T出现AOV时，便可用下式所示的模型进行表示：

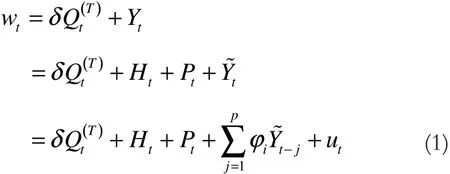
对应地，IOV的模型则如下式所示：

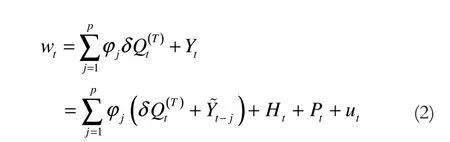
更一般地，当一个实际观测的时序数据流wt在不同时刻T1,T2,…,Tf上受到AOV或IOV的影响时，则其模型如下式所示：

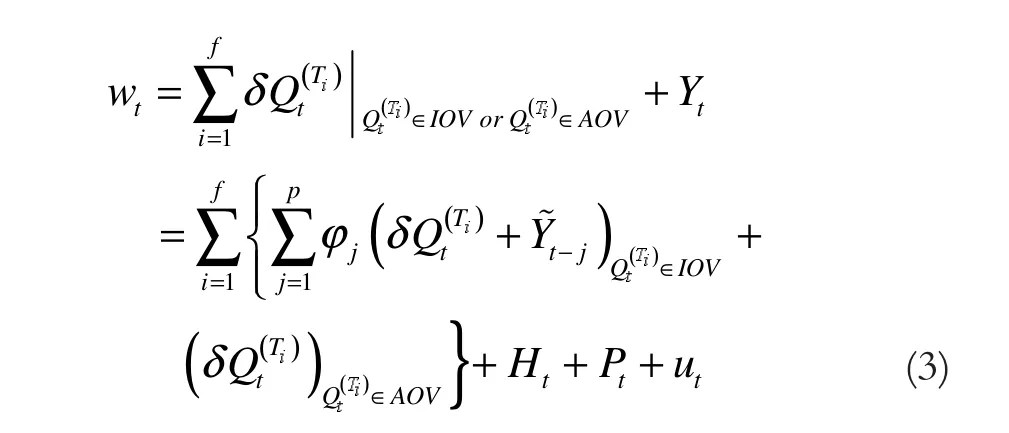
时序数据流的异常值蕴含了丰富的信息，具有重要的应用价值。系统的元部件在其生命周期的不同阶段里，其表征着物理特征的时序数据流均有不同形式的差异变化。据此，我们有必要对式(3)中的异常值发生的时刻、种类及幅值进行估计。

上世纪70年代，英国学者A.J.Fox率先对时序数据流的异常值问题展开了研究，但由于事物的动态过程有着复杂的多样性和相关性，故该领域一直以来并没有取得重要的突破[6]。近年来，随着现代信号处理技术的发展，时序数据流的异常值检测领域逐步出现了一些可用的成果。例如，吴今培及其博士生们对时间序列的稳健估计做了系统而深入的研究，并在自回归滑动平均模型 (Autoregressive and moving average model,ARMA)实现了一种有效的时序数据流异常值检测算法[7-9]；George E.P.Box和GwilymM.Jenkins基于自回归积分滑动平均模型(Autoregressive integrated moving average model,ARIMA)的残差统计量，提出了一种简便的异常值迭代检测方法[10]。针对路灯时序数据流本身固有的特点，本研究拟在上述算法的基础上，设计实现一种更为高效的异常值检测算法。

3 时序数据流异常值的改进检测算法

由于路灯时序数据流可看作某一均值与微弱随机序列的叠加，于是，在去掉均值成分后，便可以在文献[10]的基础上，改用AR模型的残差来定义统计量，进而得到一种计算效能更为高效的鲁棒迭代检测算法。

3.1 时序数据流的均值处理

在数据的统计分析过程中，经常需要使用一些统计量来表征某一要素样本的数据分布特点，而均值是一个常用的重要统计量，可作为要素总体数学期望的有效估计。以路灯时序数据流为例，要素的数据随时间的推移而不断增加，据此，有必要以递推方式来计算时序数据流的均值。

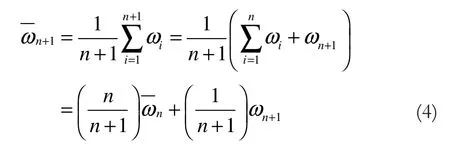
假定ω0,ω1,…,ωn所对应的随机变量为独立的正态分布变量，且具有同一数学期望，则统计量为：

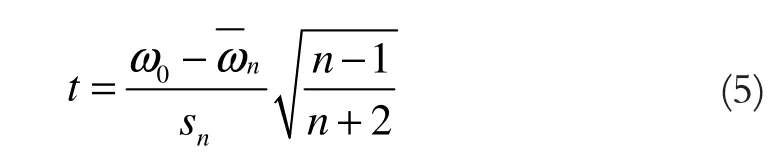
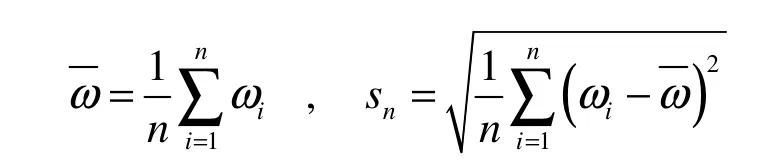
它服从自由度为n-1的t分布，其中指定相应的显著水平和自由度，查t分布表得到对应的临界值 ta，当 t＜ta，就接受原假设，认为 ω0与其它资料无显著差异；否则，就拒绝原假设，认为ω0与其它资料有显著差异。

于是，可以得到一种基于均值显著性差异的时序数据流子序列划分方法。首先，利用式(4)进行时序数据流均值的递推计算；然后，应用式(5)对加入时序数据流前后的序列样本的均值进行显著性判别，据此完成数段子时序数据流的划分。

对划分后的第j段时序子数据流ωj1,ωj2,…,ωjs进行如下式所示的去均值处理：

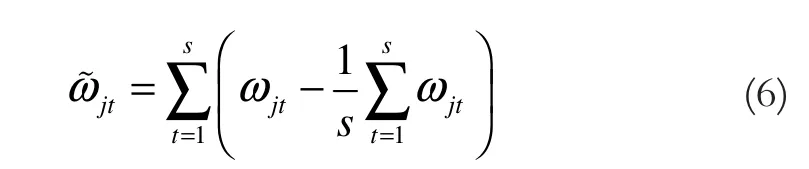
3.2 AR模型的定阶及参数估计

对于平稳随机序列而言，为了数学上处理的简便，通常都把某一时刻的数值写成以前各时期的线性组合，这种回归模型能对实际情况进行高精度的描述。用AR模型表示式(6)中的随机序列，其数学形式是：

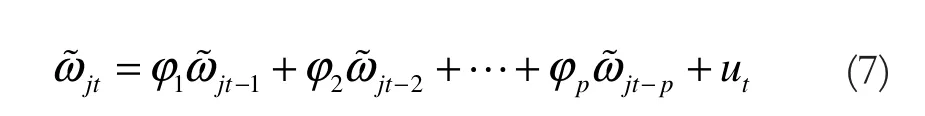
式中，p为任意正整数，称为自回归模型的阶数；φ1,φ2,…,φp为自回归参数。

求解式(7)中的自回归模型，首要的问题就是确定模型的阶数p，然后再计算对应的自回归参数。目前，自回归模型的定阶问题仍然没有得到彻底的解决，不同的判别准则将会产生不同的模型阶数[11-13]；而参数估计方面，则出现了众多成熟而高效的迭代求解算法[14]；为了提升现有的自回归模型算法的计算效能及辨识精度，黄雄波通过对辨识序列自相关函数矩阵的秩的下界值进行估计，并以该估计值为初值对系统进行依次的递阶辨识，进而得到了一种高效的自回归模型鲁棒求解算法[15]。考虑到随机序列中可能存在异常值(即是近似平稳的)，这里，引入如下AR模型的工程求解方法。

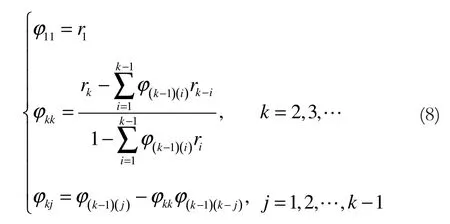
式(8)中，φkk和rk分别为随机序列的k阶偏自相关系数和k阶样本自相关系数，而自相关系数rk则用下式所示的方法进行估计：

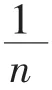
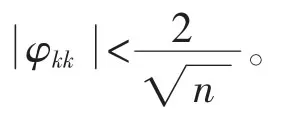
3.3 异常值的迭代检测算法

当时序数据流在某些时刻上出现异常值时，其AR模型对应的拟合位置也将出现较大的偏差，于是，对于每个时刻t=1,2,…,n而言，可以定义下式所示的两个统计量：

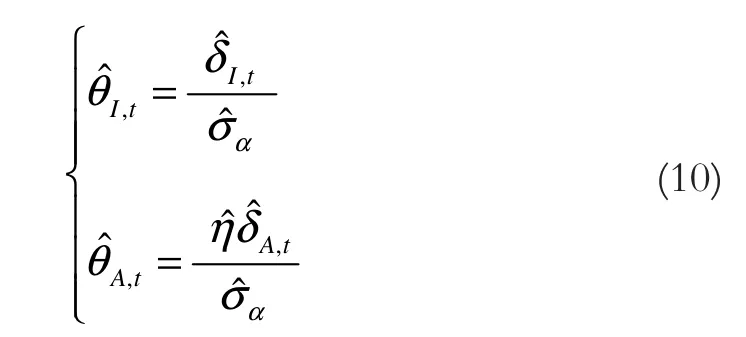
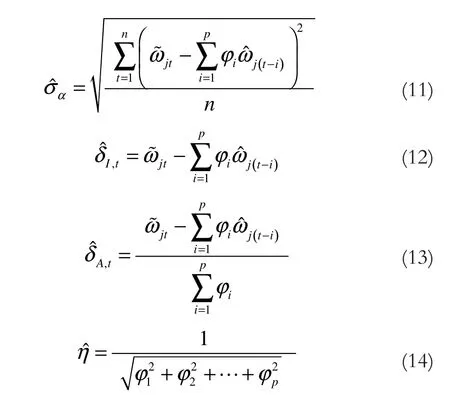
综上所述，可以设计如下的时序数据流异常值检测的改进算法：

算法名称：时序数据流异常值检测的改进算法

输入：含AOV和IOV的时序数据流wt

步骤1：利用式(4)递推计算时序数据流wt的均值，同时根据式(5)定义的统计量将wt划分为数段均值显著性有差异的时序子数据流；

步骤2：利用式(6)对步骤1析出的各时序子数据流进行去均值处理，并得到近似平稳的随机子序列

步骤3：利用式(8)、(9)对步骤2所得的随机子序列进行AR递推建模，递推结束条件为

步骤7：打印输出计算结果并结束算法。

4 实验及结果分析

4.1 实验设计

为验证上述改进算法的有效性及先进性，这里选取了两组LED灯具的温度时序数据流来进行相关的异常值检测。实验在PC机上进行，其硬件配置为：

CPU：Intel酷睿i5 4570四核

RAM：Kingmax DDR3 16GB

硬盘：Samsung 850PRO SSD；操作系统与开发环境为：

Microsoft Windows 10

Microsoft Visual Studio 2010集成开发环境中的C++。

在实验过程中，着重从检测精度和计算成本等技术指标的方面与现有算法进行对比，并就相关结果加以详细的分析和讨论。

实验样本的选取如图1、图2所示。选取LED灯具外壳温度时序数据流的正常工作、失效前兆共两种状态的样本序列进行实验，实验中需要对比的算法采用了文献[7]算法、文献[10]算法及本算法。

4.2 实验结果分析

各种算法对两种实验样本的异常值检测结果如表1所示。

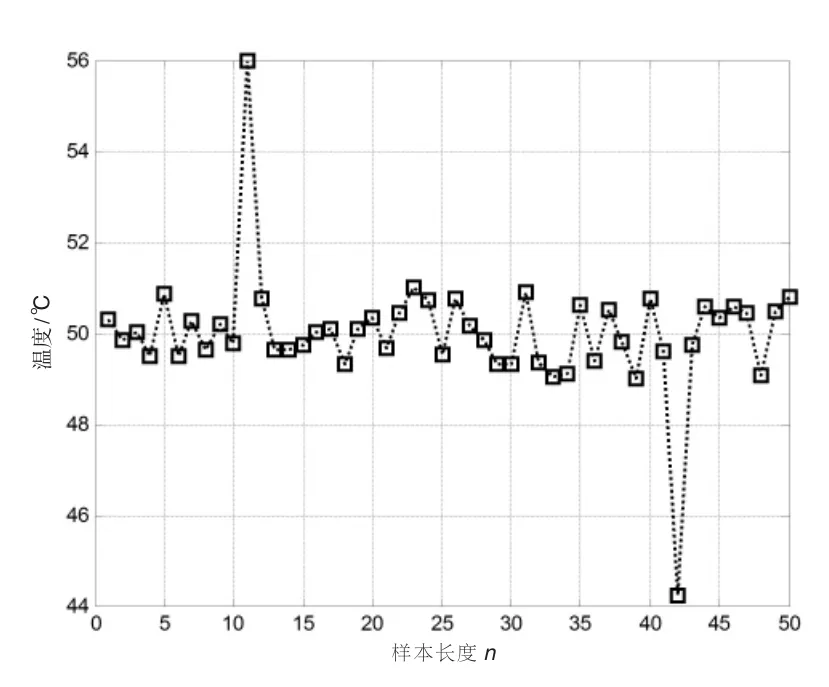
图1 正常工作时序数据流实验样本

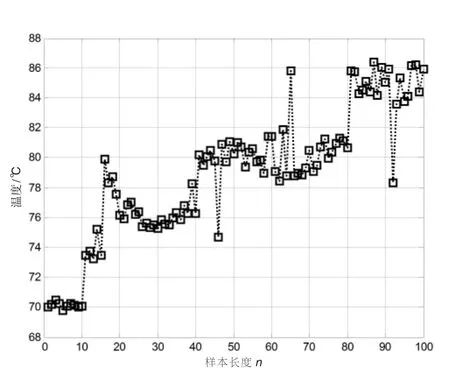
图2 失效前兆时序数据流实验样本

从表1的检测结果可知，对正常工作时的实验样本而言，三种算法均得出一致的检测结论：在时刻T1=11、T2=42处发现了AOV；所估算的异常值冲激幅值δ也处于同一水平级别，且文献[10]算法与本算法的估算结果更为接近。而对失效前兆时的实验样本而言，文献[7]算法给出了5处AOV的检测结论，所对应的时刻分别为 T1=11、T2=14、T3=46、T4=65、T5=92；而文献[10]算法与本算法则给出了这样的检测结论：在T1=14处发现的为IOV，而T2=46、T3=65、T4=92处发现的为AOV。

为了更为客观地评价各种算法的检测结果，这里以下式定义的模型残差曲线作为依据，对上述检测结论进行讨论和分析：

各种算法在两种实验样本中的模型残差曲线如图3、图4所示。从图中可以发现，对于图1实验样本而言，三种算法的模型残差曲线处于同一水平的误差范围，这也是它们一致地在相同时刻发现异常值的原因；又由于文献[10]算法与本算法均对实验样本作了平稳化处理，所以两者估算的异常值冲激幅值δ较为接近。对于图2的实验样本而言，从模型残差的角度观察，文献[7]算法结果远高于其它两种算法，且文献[10]算法结果又略高于本算法，据此，可以采纳文献[10]算法和本算法的检测结论，即在T1=14处出现IOV，在T2=46、T3=65和T4=92处出现AOV；这些异常值的冲激幅值δ应以本算法的估算结果更为可靠，即有 δ1=4.89、δ2=-5.31、δ3=3.85、δ4=-5.96。

表1 各算法异常值检测结果对比

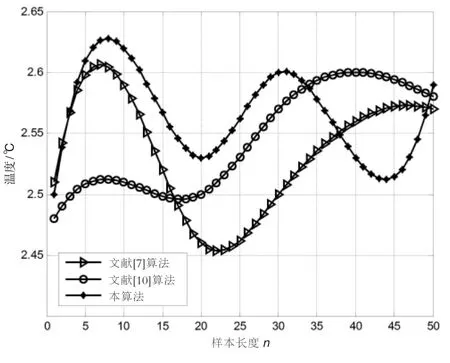
图3 各算法对应实验样本模型残差曲线（对应图1）

在实验过程中还发现，当处理的时序数据流具有良好的平稳性时，三种算法的检测性能相近；然而，随着时序数据流的平稳性变差，这些算法却有着不同的鲁棒检测性能。以图2的实验样本为例，由于LED灯具失效前兆的温度时序数据流具有强烈的不平稳性，从表1和图4易知：文献[7]算法的检测性能表现最差，分别在T1=11,T1=14处出现虚报（把状态切换点错判为AOV）和误报（把IOV检测为AOV）；而文献[10]算法与本算法的检测性能则具有一定的鲁棒性，且本算法表现得更为强壮。事实上，文献[7]算法由于直接在非平稳数据流应用ARMA模型进行建模，从而导致了建模残差增大，相应地，其检测性能也迅速变坏；文献[10]算法的差分机制及本算法的去均值处理，使得时序建模能在近似的平稳随机序列中进行，进而保障了它们的检测性能具有鲁棒性。

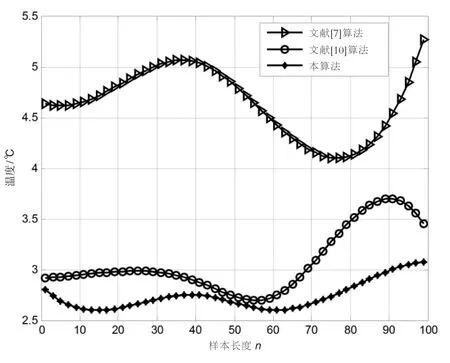
图4 各算法对应实验样本模型残差曲线（对应图2）

应该指出，本算法是根据均值显著性的差异，把图2的实验样本划分为ω1t=[1,11]、ω2t=[12,40]、ω3t=[41,82]、ω4t=[83,100]共四段子数据流，这些子数据流的均值分别为，异常值检测分别在四个子数据流独立进行。由于分段后的子数据流具有更好的平稳性，据此，本算法的建模精度能进一步得以提升。

各种算法的计算耗时如表2所示，其中，本算法所花费的计算耗时略小于文献[7]算法和文献[10]算法。由于文献[7]与文献[10]的异常值检测算法均基于ARMA模型，且ARMA模型的参数估计又需要求解高阶非线性方程组，需要花费相当的计算耗时;又由于文献[10]算法还需要进行差分预平稳处理，故它比文献[7]算法花费了更多的计算成本。与上述算法不同的是，本算法的检测模型替换为AR模型，由于AR模型的求解有成熟的递推算法，故此节省了一定的计算成本，事实上，本算法时间主要是在消耗在均值显著性判别、分段划分及去均值等处理上。

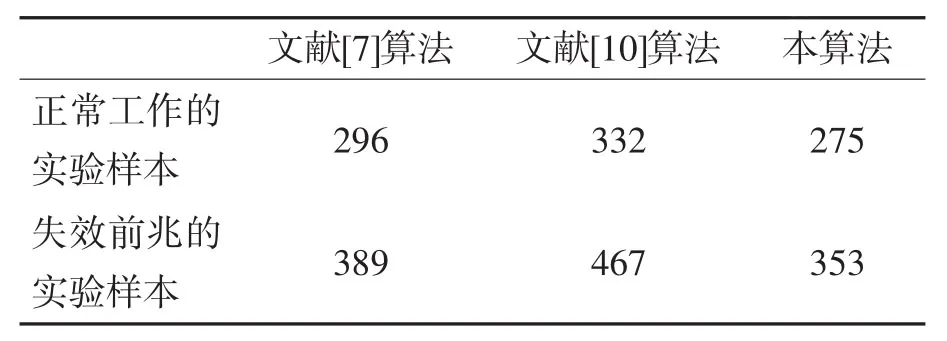
表2 各算法计算耗时对比 单位：ms

从如上分析可知，本算法较现有的异常值检测算法而言，在不增加计算成本的同时其检测精度及算法鲁棒性均有了一定的提升。据此，本算法是正确和有效的。

5 结束语

针对路灯时序数据流具有均值缓变的特点，提出了一种基于均值显著性的异常值分段检测算法，从实验得知，该改进算法在没有增加计算成本的情况下，其检测精度及算法的鲁棒性得以提升。在本研究的基础上，还有待做出进一步的工作，针对形式多样的高度非线性和非平稳的时序数据流，研究更为有效的线性化及预平稳处理机制，同时，将已有的异常值检测算法应用至时序数据流的压缩，以便进一步提升算法的应用效能。