非线性回声消除之收敛性分析*

杨瑞丽，郭 莹

（沈阳工业大学信息科学与工程学院,沈阳110870）

1 引言

声学回声一直是影响通信质量的关键问题[1-2]。目前，典型的回声消除器设计都在假设回声路径是线性的，可以采用有限长脉冲响应（FIR）滤波器进行建模。然而，近几年，随着低成本小型设备在免提手机和视频会议等应用中的广泛使用，放大器和扬声器引入非线性回声的问题日益严重[3-4]。这种非线性回声难以由传统的线性回声消除器消除，回声路径中存在的非线性也会限制线性滤波器的性能，干扰声学脉冲响应的正确估计，降低语音信号的感知质量[5-6]。因此，如何消除非线性回声日益成为信号处理领域的研究热点[7-10]。

目前，虽然已有部分学者研究了很多非线性回声消除法，但其都缺少相应的收敛性分析。为此，新提出的一种非线性回声消除方法，在此基础上，进一步对非线性滤波器系数和线性滤波器系数进行详细的收敛性分析，并进行了大量的MATLAB实验仿真，验证对非线性回声消除的收敛性分析的合理和可行性。

2 非线性回波消除

本研究采用基于Hammerstein模型的无记忆非线性回声消除方案，以非线性滤波器建模非线性器件，以线性滤波器建模线性回声路径。系统整体构成原理如图1所示。

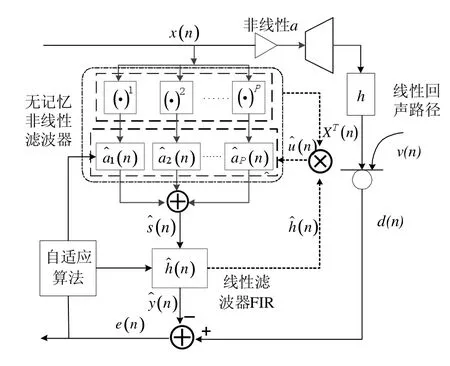
图1 非线性回声消除系统

对于无记忆非线性滤波器，采取一种级数展开的截断模型来描述，如下式所示：

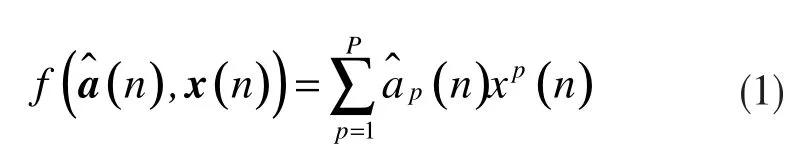
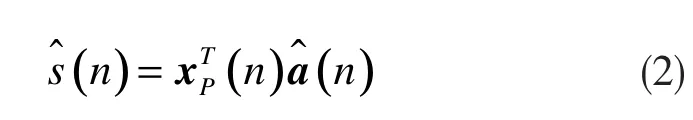
其中，

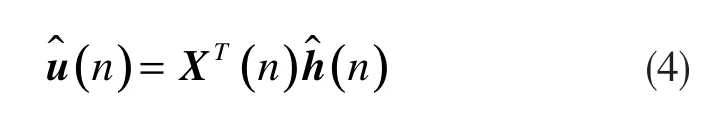
这里，

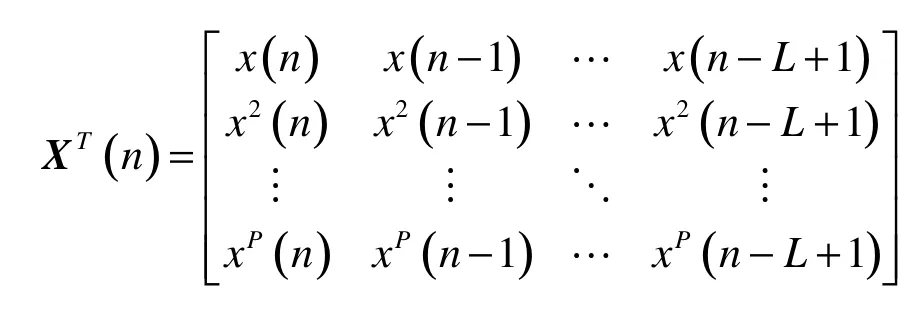
由式(2)、(3)、(4)可以得到：

此处所用的两个滤波器的自适应算法均采用NLMS算法，非线性滤波器系数的级联NLMS迭代方程如下式：

相似地，线性滤波器系数的迭代方程可以表示为下式：

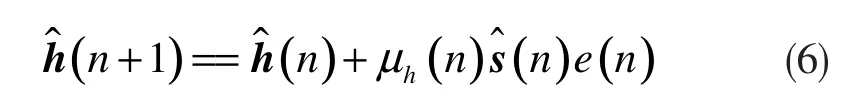
3 完美假设下的收敛性分析

3.1 线性系数误差的收敛性分析

完美假设指的是滤波器系数对未知系统的估计是完全匹配的，这里是假设非线性系数估计完美时即，来对线性系数误差进行收敛性分析。

线性系数误差和非线性系数误差分别表示如下：

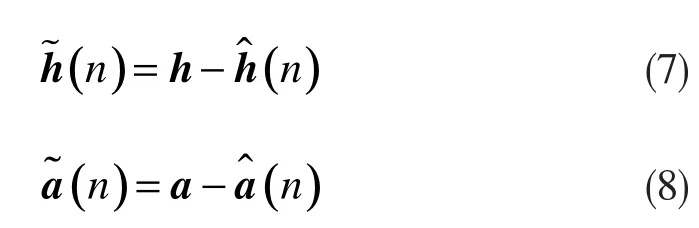
公式(7)又可以表示为：

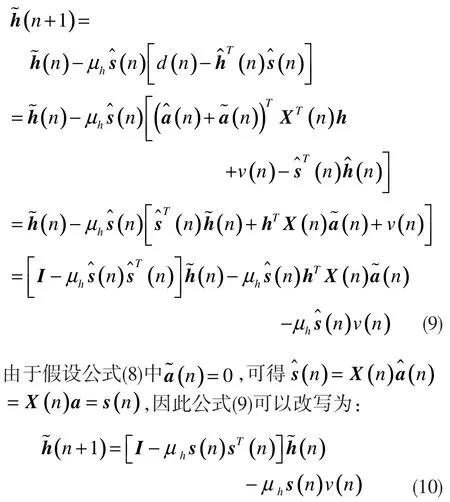
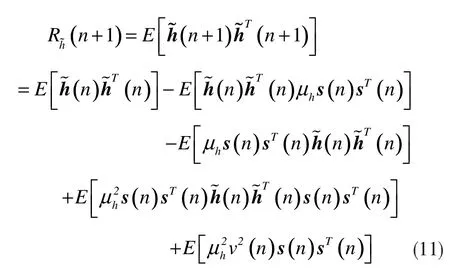
这里假设系统中的近端噪声v(n)是零均值且独立的，即这两项不存在。

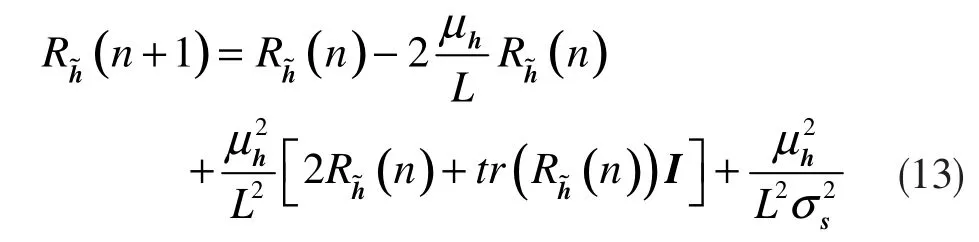
对其取迹可得：

通过递归，公式(14)可以重新表示如下：

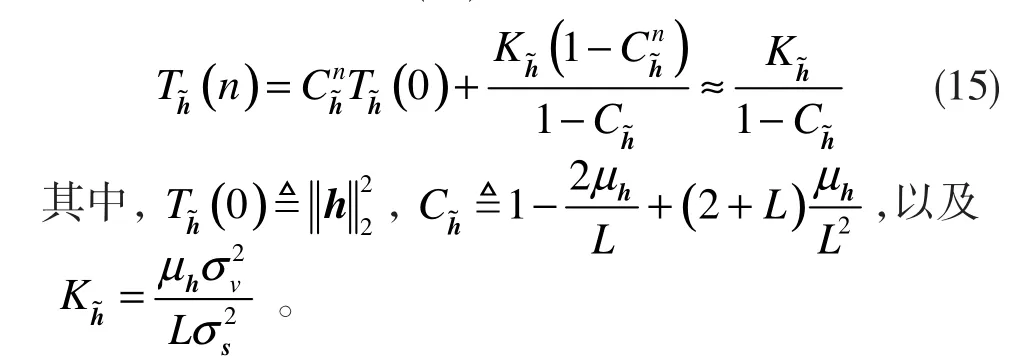
3.2 非线性系数误差的收敛性分析

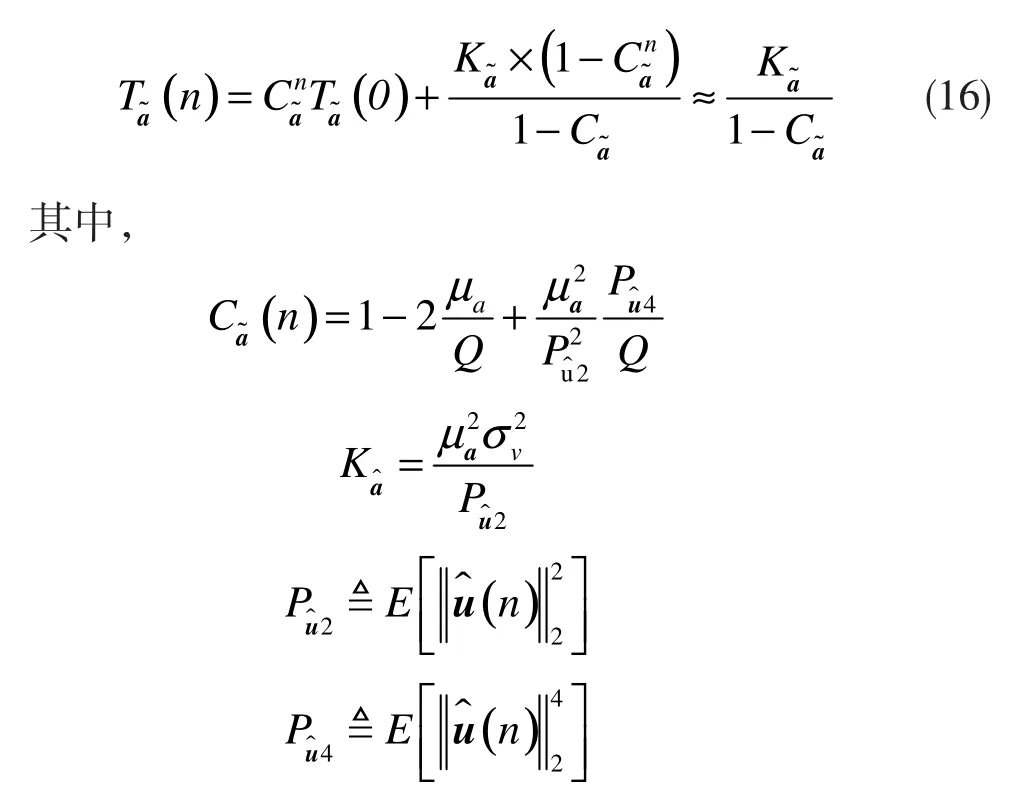
4 不完美假设下的收敛性分析

4.1 线性系数误差的收敛性分析

在此不再假设非线性系数是完美估计，而是考虑到了非线性系数的估计误差所产生的影响。公式(9)将会成为线性参数的更新方程，有以下关系，其中

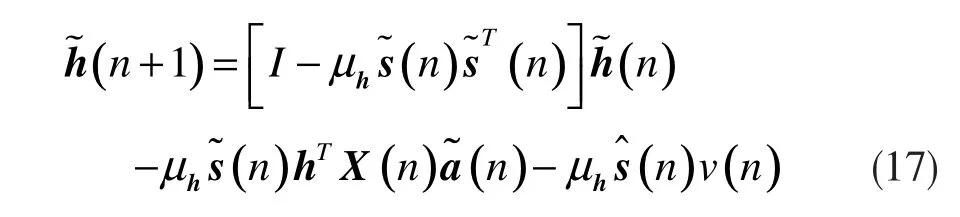
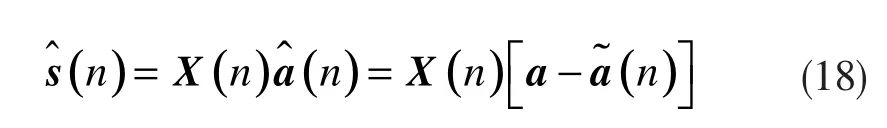
将线性系数估计误差的相关矩阵划分为两个部分，可以将其重写为：

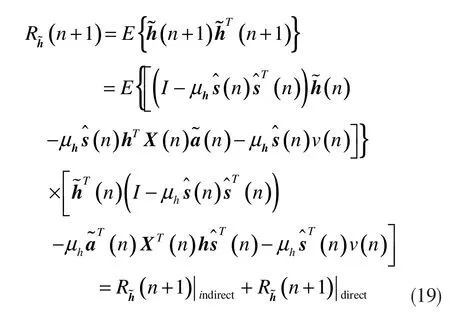
由于假设非线性系数的估计误差和线性系数的估计误差的期望值均为零，以及当地噪声的均值也为零，在此条件下，公式(22)中只保留了第五项，即如下式表示：

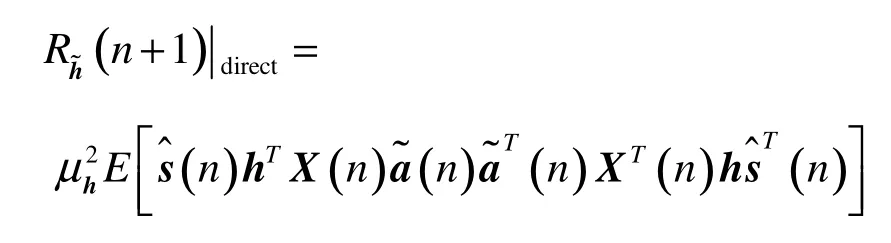
将公式(18)和线性滤波器的输出代入公式(22)中，其可以被重写为：

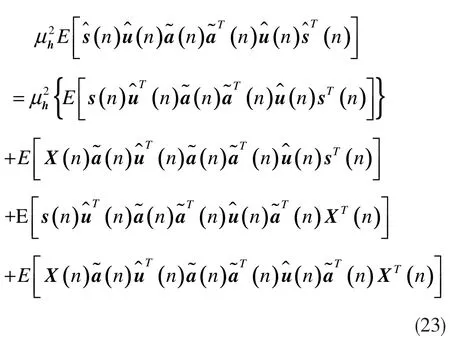
综合以上分析，公式(19)可以重写表示为：

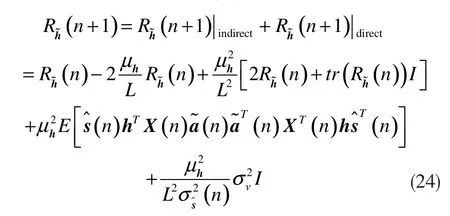
接下来，对公式(24)进行求迹，

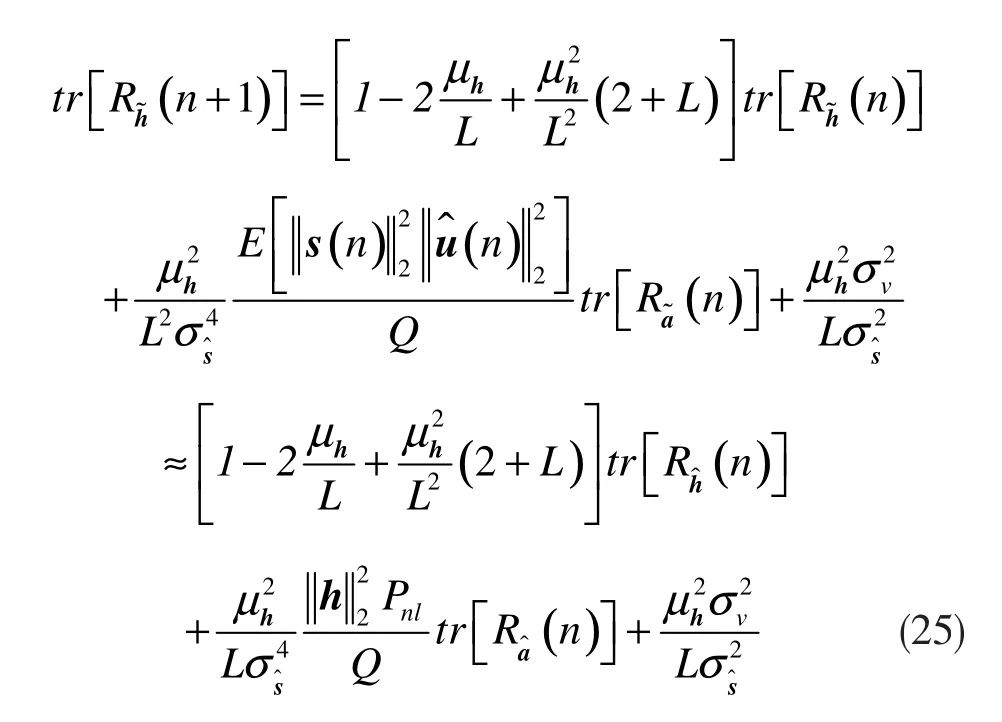
当Q=3时，

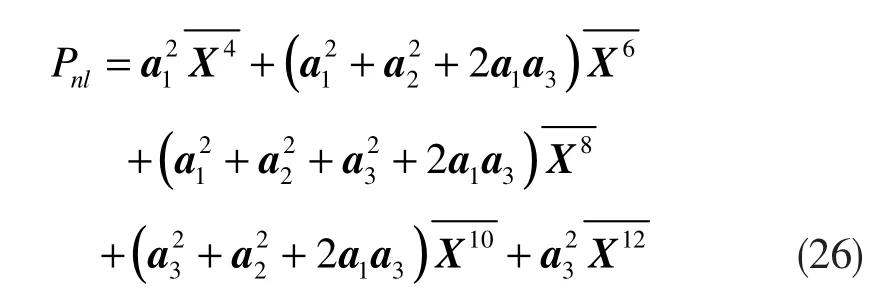
4.2 非线性系数误差的收敛性分析

在不完美假设下对非线性系数误差进行分析，其过程与在4.1中类似，

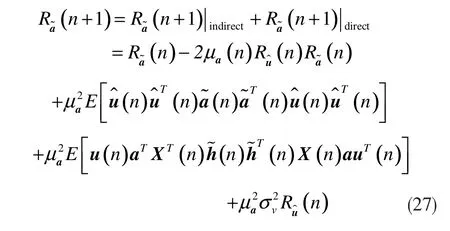
接下来，对此式求迹，具体表示如下：

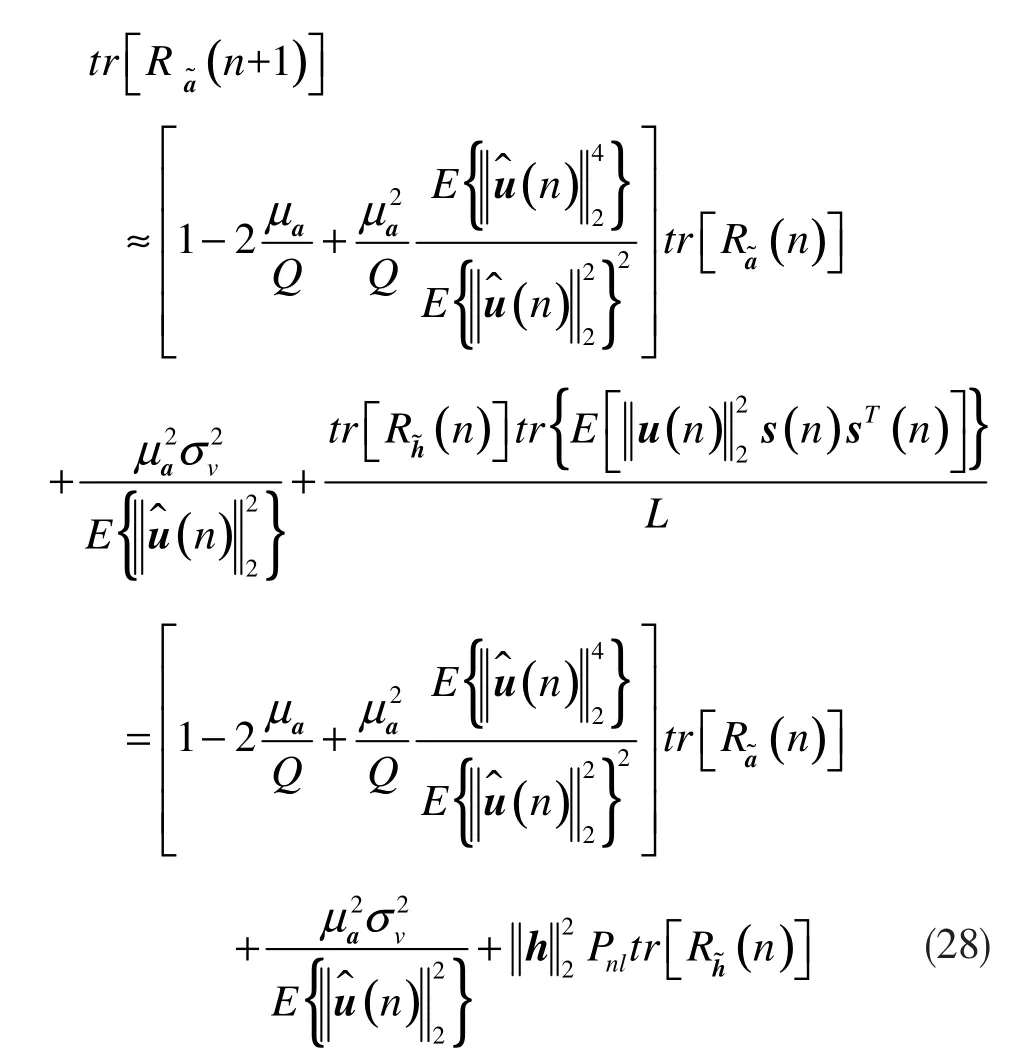
当Q=3时，

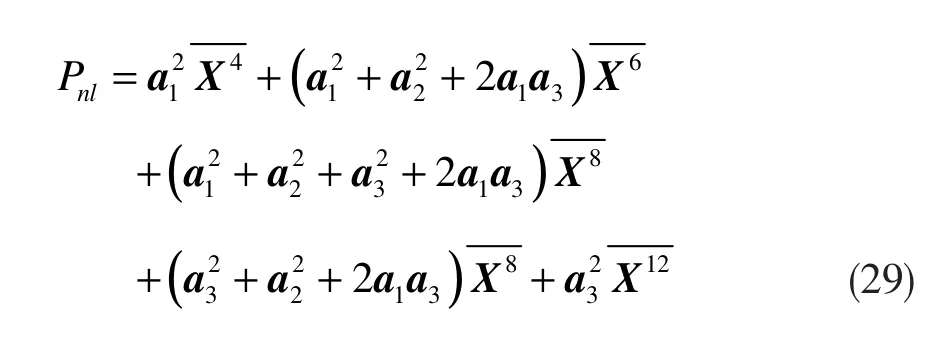
5 仿真实验

5.1 仿真条件

在仿真中，采用零均值的高斯白噪声作为系统的输入信号。无记忆非线性滤波器的阶数取3,FIR滤波器的长度和线性声学回声路径的长度一致，均为128。背景噪声采用20dB的高斯噪声。无记忆非线性系数向量定义为a=[1.0,0.1,0.33]T，线性声学回声路径可以由下式产生[11]：

其中，n,i=0,1,...,L-1,L为脉冲响应长度，r(n)为[-0.2,0.2]的随机数，δ为Dirac函数，L取128。如图2所示。

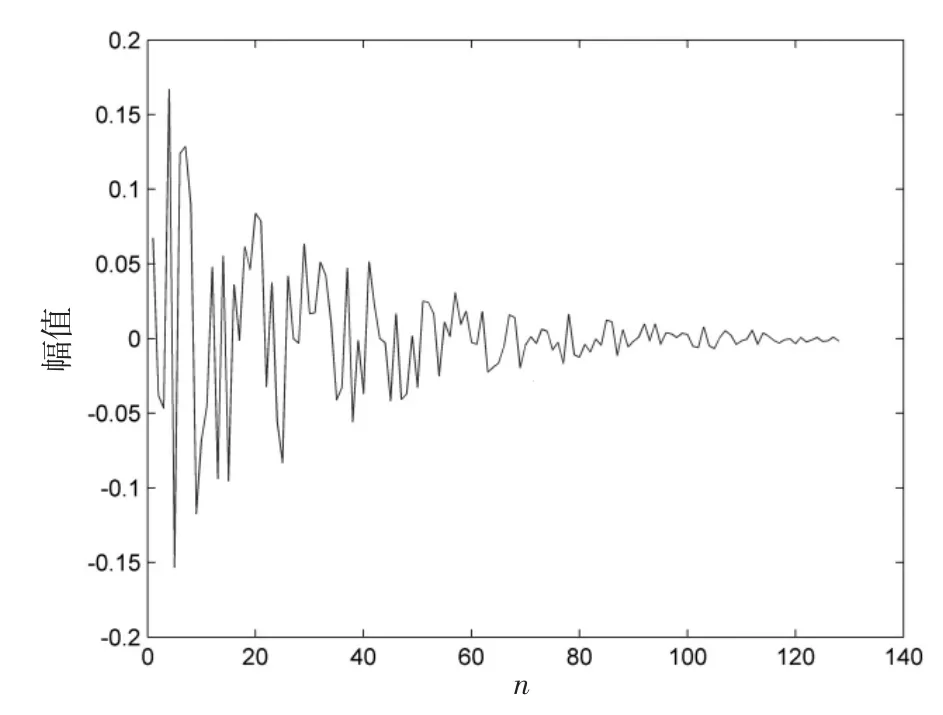
图2 声学回声路径脉冲响应h

在初始化时，a与h不同，h初始化为零向量，而a初始化为[1,0,0]。

5.2 性能指标

非线性系数的权误差向量范数WEVN表达式为：

线性系数的WEVN表达式为：

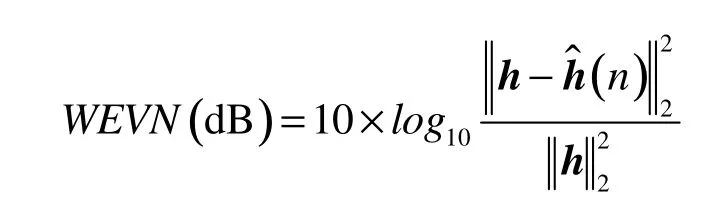
WEVN的值越小则说明自适应滤波器越逼近于所跟踪的未知系统。

5.3 仿真结果分析

仿真生成曲线与理论曲线的对比情况如图3、图4、图5和图6所示，分别对应为公式(15)、公式(16)、公式(25)和公式(28)。

从图3～图6可以得出，无论是在完美假设条件下，还是在不完美假设条件下，线性系数和非线性系数误差的仿真结果与理论结果之间的误差保持在3dB左右，可以说明文中对线性滤波器系数和非线性滤波器系数的收敛性分析是合理的，这对非线性回波消除的研究具有很重要的意义。而且，在实际生活中有很多场合都会存在非线性回声，比如，免提通话系统，视频会议系统等。对于有关提高电信设备通话质量的研究，此仿真结果可提供有力的参考。

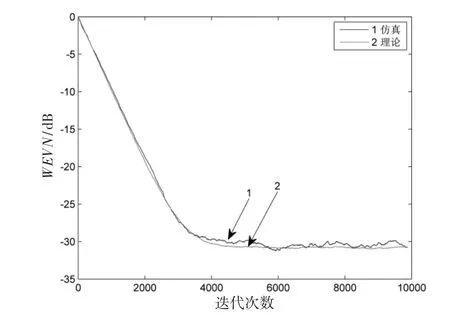
图3 完美假设下线性系数误差收敛曲线

图4 完美假设下非线性系数误差收敛曲线

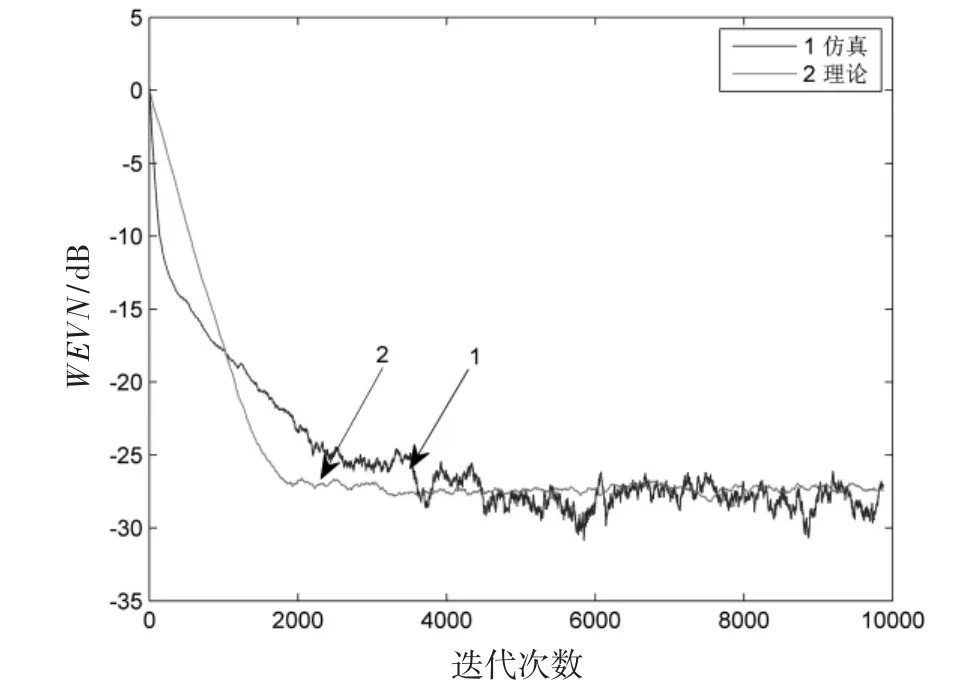
图5 不完美假设下线性系数误差收敛曲线

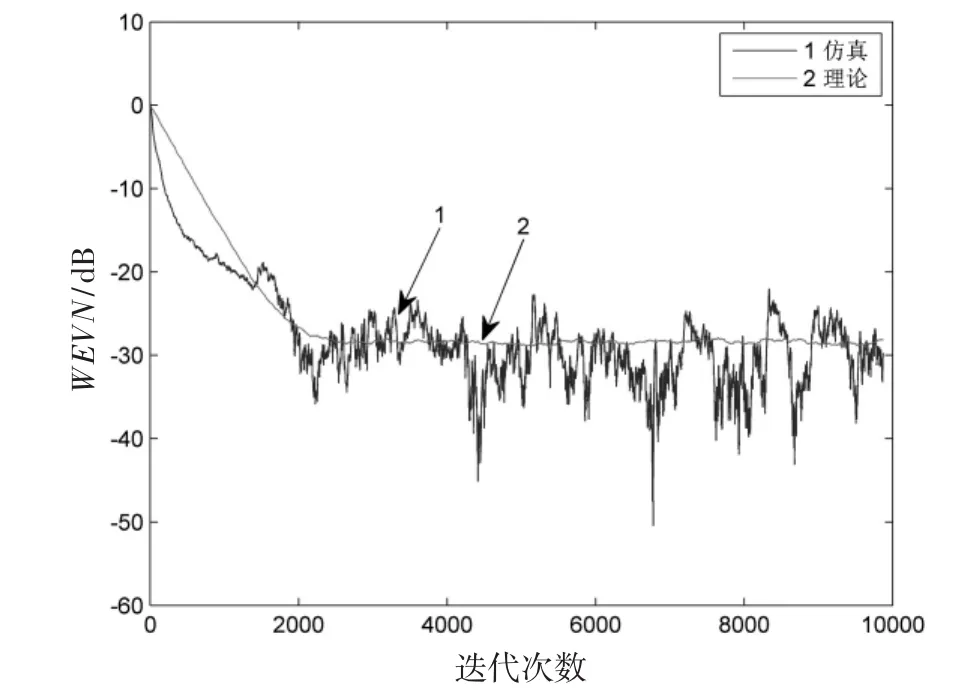
图6 不完美假设下非线性系数误差收敛曲线

6 结束语

本研究在提出一种新的非线性回声消除方法的基础上，在完美假设和不完美假设的两个方面分别对线性系数误差和非线性系数误差进行了详细的收敛性分析，并进行了相应的MATLAB实验仿真，与理论值进行对比，验证了对线性系数误差和非线性系数误差的收敛性分析的合理性，对于非线性回声消除的进一步研究具有非常重要的意义以及实用价值。