远距离支援复合干扰空域规划研究
2019-01-03王晴昊姚登凯赵顾颢王红卫
王晴昊, 姚登凯, 赵顾颢, 王红卫
(1.空军工程大学 研究生院, 陕西 西安 710051; 2.空军工程大学 空管领航学院, 陕西 西安 710051;3.空军工程大学 航空工程学院, 陕西 西安 710038)
在战场环境下,雷达获得战场态势可以极大地发挥武器的杀伤效能,为了提升作战飞机的生存能力,需要对敌方雷达进行干扰。对敌方地对空制导雷达主要的干扰方式有远距离支援干扰和无源干扰。远距离支援有源干扰由于其发射干扰功率大,形成的压制效果好而得到广泛使用,但是其干扰信号主要从副瓣进入而旁瓣对消或低副瓣等抗干扰措施使得干扰的效果大为降低。箔条无源干扰也由于动目标显示(moving target indication,MTI)等抗干扰技术的应用其干扰效能大为降低,但是其干扰信号能从主瓣进入,考虑到2种干扰方式的优点和缺点,拟将2种方式复合使用以增强对新式雷达的干扰效果。在干扰新式雷达的研究方面,文献[1]主要指出远距离支援干扰对新式雷达干扰效能较差,文献[2]提出可以利用欺骗干扰对其进行干扰,文献[3]指出可采用航迹协同的方法来干扰相控阵雷达,但是这种方法会较多地占用干扰资源,对飞行员的操纵性能要求较高。复合干扰逐渐得到相关学者的重视,陈静最早在其著作中提到复合干扰技术并进行了可行性验证分析[4-5],杜建东等人对混合式和转发式复合干扰在单舰艇反导防御中的战术运用进行了探讨[6],唐政等人对照射箔条的复合干扰对提高干扰效果进行了分析[7],罗朝义等人就复合干扰对机载相控阵雷达的压制比进行了计算分析[8]。以上研究主要集中在复合干扰可行性和干扰效能分析方面,结合电子干扰作战的实际运用方式来进行相关研究的文献很少。
基于上述研究现状,本文提出一种新的复合干扰方式在研究远距离支援干扰空域规划的相关概念及其影响因素的基础上,通过对复合干扰原理研究、箔条云RCS计算,分析复合干扰效能及其应用所需条件,建立远距离支援复合干扰空域规划模型,针对该模型设计一种基于混沌序列的鲸群优化算法并对其进行解算,最后,进行仿真验证。
1 远距离支援干扰空域规划
1.1 远距离支援干扰空域规划原理
远距离支援干扰在空中作战中发挥着重要作用[9],主要由专门的远距离支援干扰飞机在固定高度上作跑道型或“8”字型飞行,对敌防空预警以及指控系统进行雷达或通信干扰,以支援和掩护航空兵遂行空中进攻作战任务。而其效能发挥的关键在于规划合理的空域。在规划空域时要考虑到敌我态势、上级指挥意图、被掩护目标航线以及干扰机的性能等因素,其规划的过程可简要归纳为“点、线、向、面”。
1) “点”即确定最佳的空域基准点,也就是能够充分发挥干扰机作战效能的最佳位置;
2) “线”根据被掩护目标的航线、飞行参数,干扰机的飞行参数、干扰航线(本文研究的飞行方式为跑道型)和干扰天线的布设方式(本文选取干扰天线布设在机身两侧)、飞行误差等确定干扰飞机的最大偏离航线以及空域的4个边界点与基准点的关系;
3) “向”即在确定空域的最佳基准点、最大偏离航线以及空域的4个边界点与基准点的关系,寻找最佳的干扰空域方向;
4) “面”,确定“点”、“线”、“向”之后规划出空域的具体摆放位置,其形状为条状。
1.2 远距离支援干扰空域的影响因素
如1.1节所述,在确定最大偏离航线时需考虑飞行误差的影响,干扰飞机一般是特制的大中型飞机改装而来,与民航大中型运输机相类似,其飞行误差因素主要有人为因素、空中风以及导航设施,而在干扰机实施干扰过程中,主要在空中预警指挥平台的统一指挥下实施干扰,它们之间依靠数据链进行指挥通信,因此导航设施的误差可忽略不计,只考虑人为因素和空中风的影响。关于人为因素和空中风对航线的影响,已有大量文献对进行描述,本文不再赘述,具体可参见文献[10]。其计算公式如下:
人为因素:
(1)
风的影响为:
XW=(α/ω)·(VW/3 600)
(2)
飞机的偏离量可计算为:
XE=XA+XW
(3)
A0为飞行员的预定操纵动作,A为飞行员的实际操纵动作,σa为方差,XA为人为因素偏离量,α为转弯角度,ω为角速度,VW为风速,XW为风产生的偏离量。
2 复合干扰原理及效能分析
2.1 复合干扰原理
如引言所述,本文拟将远距离支援干扰飞机的较强干扰功率,和箔条云团的强散射能力结合起来,使远距离支援干扰飞机的干扰信号从敌方雷达天线主瓣散射进入接收机,从而大幅提高干扰效果。具体方法如下:
远距支援干扰飞机掩护突防编队到达敌地对空制导雷达探测范围之外,在目标雷达、突击飞机一线上释放箔条弹形成箔条云,如图1所示。

图1 复合干扰示意图
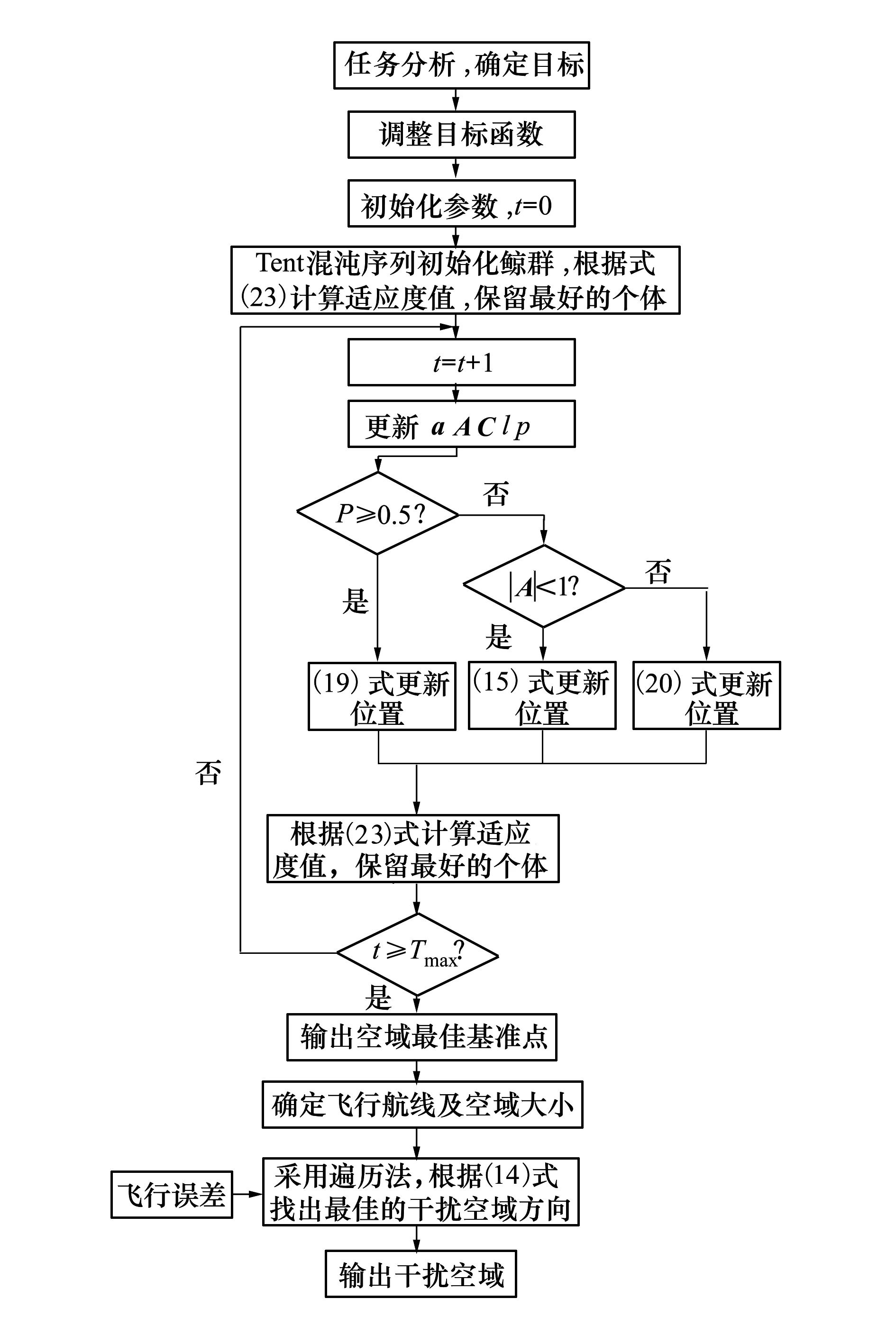
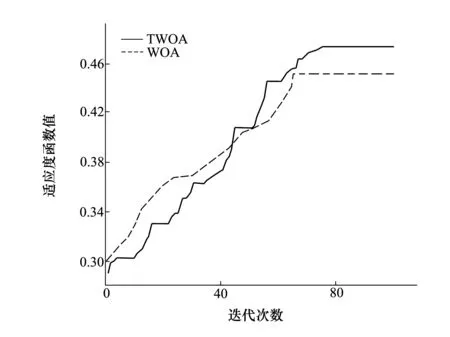
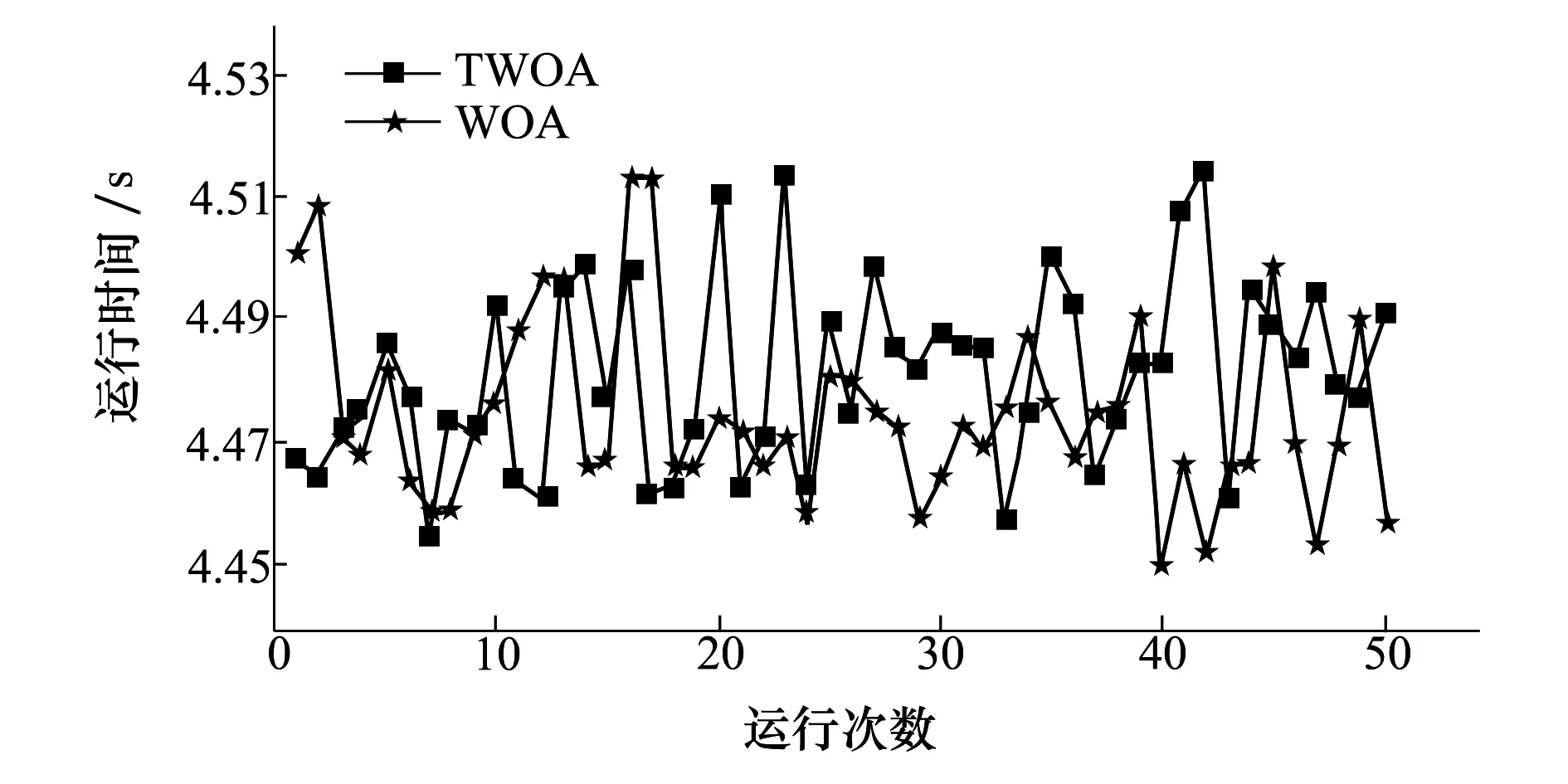
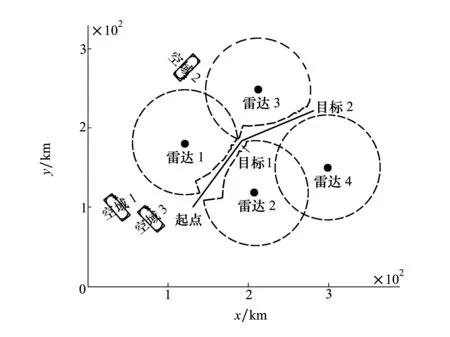
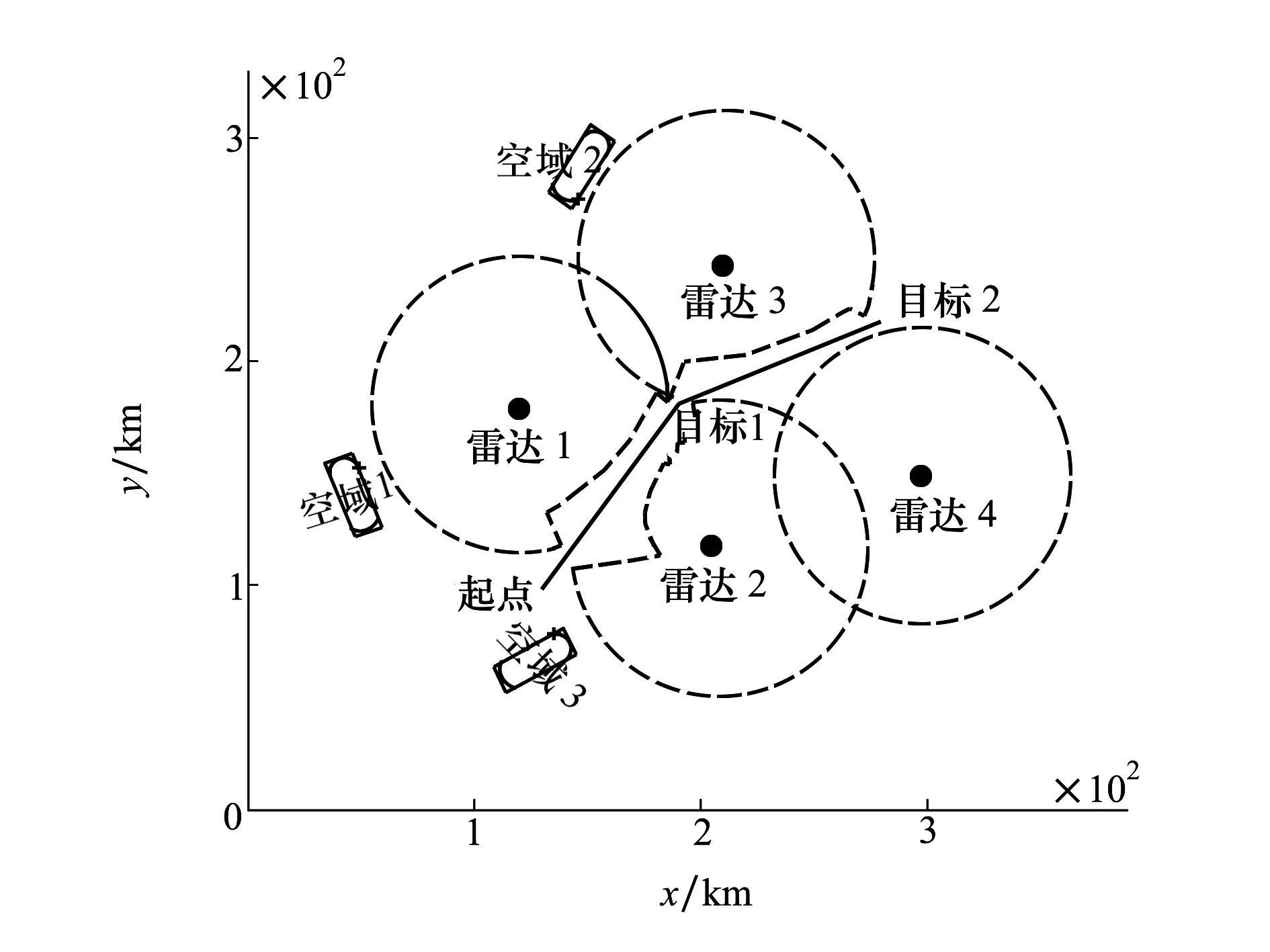
图中的R为雷达的探测范围,R1为远距离支援干扰机与雷达之间的距离,R2远距离支援干扰机到箔条云之间的距离,Rx为箔条云(或突防飞机)到目标雷达之间的距离。在突防过程中,为打击突防飞机,敌方利用制导雷达进行探测定位,为了锁定我突击飞机,敌方雷达一般会使其天线主瓣持续直接照射突击编队,那么突击编队尾部的箔条云团同样也在雷达天线主瓣范围之内,则有Rx 利用箔条对雷达进行干扰时,需着重考虑的是箔条云平均散射截面,其计算通常由电磁学理论计算单个箔条振子(通常为半波长振子)继而推导统计到整个箔条云。设箔条为半波长的导线,入射的电磁波电场强度E与箔条夹角为θ,则半波长箔条的有效反射面积为 σλ/2=0.86λ2cos4θ (4) 假设电磁波为水平极化波,箔条在三维空间内呈任意分布状态,设Ω为立体角,W(Ω)为角Ω的概率分布密度,箔条的平均有效反射面积就应将σλ/2对整个空间的立体角求平均即 (5) 考虑箔条云的互耦效应以及损坏,则一个箔条弹的总有效散射面积约为 (6) 式中,λ为波长,N为箔条的根数。 根据2.1节的原理分析,在实施复合干扰时,雷达将接收到2种干扰信号:①目标直接反射到雷达的信号;②远距离支援干扰飞机将强烈的干扰信号照射到箔条上继而转发的干扰信号。由雷达方程可知,雷达接收的目标回波功率为: (7) 由远距离支援干扰飞机转发的干扰信号照射到箔条云上的干扰信号功率为: (8) 由箔条云转发并为雷达所接收的干扰信号为: (9) (10) 形成安全穿越区域的宽度为: (11) 需注意的是在突防过程中,要使复合干扰必须满足W>0否则无法发挥作用,即 推出R2和Rx之间的关系为 (12) 则雷达与箔条云之间的最大距离 (13) 由公式(12)可知,应用该种复合干扰的条件是:①干扰机发射有效功率要足够强,并且箔条云的有效散射截面与目标的散射截面要足够大。这个条件并非难以满足,是因为电子干扰飞机本身辐射的有效功率非常强,如果其功率不能达到要求,可以采取特殊技术增强电子干扰机有效辐射功率或采用多架电子干扰飞机进行编队飞行。箔条弹的质量轻、根数多,短时间能够形成较大的散射截面,即使箔条云平均散射截面与目标散射截面的比值较小,可以对突防飞机涂抹特殊材料减少其散射截面以及同时释放多个箔条弹而得到解决。这是技术问题,在此不做过多讨论。②干扰机与箔条云的距离和箔条云与被干扰目标的距离之间的比值要适中,不能超出最大比值。③形成成熟箔条云时间要尽可能短,但是有效持续时间应满足额定要求,以便能持续对雷达形成干扰。现有的机载投放装置以及箔条能够满足这2个需求。④远距支援干扰飞机的机载有源干扰天线应持续保持指向和跟踪箔条云(或突防飞机),使干扰能量能够持续得到转发,这需要突防飞机和远距离支援干扰飞机之间具有良好协同性。由于远距离支援干扰飞机通常与预警指挥飞机配合使用,因而突防飞机与远距离支援干扰飞机的实时协同问题能较好地实现。⑤突防飞机必须准确控制好投弹时机,当飞离压制区域时应立即释放箔条弹。 在遂行突防任务的过程中,通常需要对敌纵深目标进行打击,假定在某次作战中,需要按照上级指定的航线,对敌重要目标(图2中的目标1和目标2)实施打击,为了直观展示其具体过程,以虚线圆圈代替雷达未受干扰的探测范围,以实线线段代替我方突防战机预设的航线,以实小圆点代替威胁雷达的具体布设位置。 图2 攻击任务示意图 由图2可知,在遂行此次作战任务中,突防飞机将长时间暴露在敌方雷达探测范围内,遭受对方地对空武器攻击的概率极大,为保证任务的顺利完成,需要电子干扰飞机对敌地对空制导雷达压制,形成可飞行的安全穿越区域。因而,需要规划远距离支援干扰空域,以往的规划方法主要依靠指挥员的个人经验,有可能造成干扰空域规划干扰效果不够理想,同时可能造成空域的浪费影响其他作战空域的规划。 故而,需在明确敌我双方态势情况下,应用2.1节所介绍的复合干扰方式,在预警机指挥控制区域内与突防飞机协同完成打击任务,结合空域规划的方法以及其影响因素,建立量化的远距离支援干扰复合空域模型,依据相关参数合理确定空域位置和规划空域的大小,目的是使攻击战斗机能够按照预定突防航线安全穿越威胁地带,完成攻击任务。 依据3.1节的描述,在规划远距支援干扰空域时,应当考虑远距离支援复合干扰对敌方雷达的干扰效果,合理确定空域的位置、大小和朝向,使得突防飞机能够按预定航线飞行而不遭受敌地对空武器的攻击,使得突防航线与雷达探测范围的最小距离尽可能大,并且考虑到整个突防任务,又要使其压制作用尽可能的均匀,同时由于远距离支援干扰飞机属于十分珍贵的作战资源且其机动性能较差,因此,要考虑电子干扰飞机的安全性,在保证不被雷达探测以及在预警机的指挥控制区域内,还不能使其距离威胁雷达的中心过近,但又不能超出其能够发挥远距离干扰效能的最大距离,于是有以下数学模型: (14) 在实际规划空域时,还需满足的约束条件如下: 1) 安全约束:干扰机须配置在各个雷达的探测范围之外则有 2) 有效干扰约束:干扰机与箔条云的距离必须小于其发挥效能的最大距离 R2j 3) 指挥控制约束:干扰机的配置必须服从指挥员的配置要求 根据3.2节所建立的数学模型可知,其是一类非线性优化问题,智能优化对该类模型的求解十分快捷有效。澳大利亚的学者Mirjalili等[13]受座头鲸bubble-net捕食策略的启发,提出了一种结合包围收缩以及螺旋式更新的鲸鱼优化算法(whale optimization algorithm,WOA)该算法由于调节参数少、结构简单、运行速度快,寻优能力强,已在许多特定优化问题的求解上得到了应用[14-15],但是与其他优化算法一样易陷入局部最优,因而需要对其改进以降低陷入局部最优的概率。 WOA算法的原理主要是模仿座头鲸的包围、猎杀、搜索的3种行为,对猎物进行包围时,其位置更新如下: X(t+1)=X*(t)-A·|C·X*(t)-X(t)| (15) A=2a·r-a (16) C=2r (17) a=2(1-t/tmax) (18) t为当前迭代次数,tmax为最大迭代次数;A和C是系数向量;X*(t)为当前获得的最佳鲸群个体空间位置;X(t)为当前鲸群个体空间位置;a表示在勘探和开采阶段由2到0线性递减,r=rand()为[0,1]上的随机向量。 座头鲸在攻击猎物时还要以螺旋运动的方式靠近猎物,因此在WOA算法中以0.5的概率进行螺旋运动因此有 (19) 式中,b为对数螺旋形状常数,l为[-1,1]之间的随机数。若p<0.5,则按(15)式更新位置。 由(15)式可知包围猎物时,位置的更新取决于a的变化对A向量的影响,同样的变化过程在搜索阶段依然适用,当|A|>1时,进入搜索阶段,为了保证搜索的随机性,采取随机生成位置的方式,在一定程度上使WOA搜索更全面,其位置更新为: X(t+1)=X(t)rand-A|C·Xrand(t)-X(t)| (20) 式中,X(t)rand是从当前鲸群中随机选择的向量位置(随机鲸群个体)。 群智能优化算法的初始化会影响算法的精度,而WOA算法的初始化是随机生成的,可能使算法陷入局部最优。而混沌序列由于具有伪随机性、遍历性、有界性的特点,能够提升算法的求解精度,降低算法陷入局部最优的概率[16]。目前,最为常用的产生混沌序列映射有Tent和Logistic,而已有公式严格证明Tent序列映射比Logistic序列优,并且计算简便。其计算公式如下: (21) 经伯努利变换之后的表达式为 yn+1=(2yn)mod1 (22) 其具体产生方法在文献[15]中已有详尽描述,不再赘述,仅提供核心代码如下: function[Y]=Tent-Chaos(TC-no,dim) Y=zeros(TC-no,dim); fori=1:dim y=rand; forj=1:TC-no ifj==1 Y(j,i)=y; else ifY((j-1,i)==0‖Y((j-1),i)==0.25‖Y((j-1),i)==0.5‖Y((j-1),i)==0.75‖... (j==3&&Y((j-1),i)==Y(((j-1)-1),i))‖(j==4&&Y((j-1),i)==Y(((j-1)-2,i))‖... (j==5&&Y((j-1),i)==Y((j-1)-3,i))‖(j==6&&Y((j-1),i)==Y(((j-1)-4),i)) Y((j-1),i)=Y((j-1),i)+0.1*rand; if 0<=Y(j-1),i&&Y((j-1),i)<=0.5 Y(j,i)=2.*Y((j-1),i); else Y(j,i)=2.*(1-Y((j-1,i)); end else if 0<=Y((j-1),i)&&Y((j-1),i)<=0.5 Y(j,i)=2.*Y((j-1,i); else Y(j,i)=2.*(1-Y((j-1),i)); 根据4.1和4.2节所述以及本文所建的模型,其求解步骤如下: 步骤1 对电子干扰飞机和突防飞机的任务进行分析,明确干扰目标 步骤2 调整确定目标函数。由于WOA是求解极小值,因此将(14)式的负数作为目标函数(在存储数据时,记录的是程序运行所得负值,即所建模型实际取得的值),对指挥控制约束采用区域限制的方法进行满足,而对安全约束和有效干扰约束采取惩罚函数的方法对其满足: (23) 式中,f为(14)式中的适应度函数,P为无穷大。 步骤3 初始化算法参数。设置群体数目N、维数D、最大迭代次数tmax,对数螺旋形状常数b、算法的终止条件,并在解空间内采用Tent混沌序列初始化鲸群个体空间位置,令t=0。 步骤4 利用(23)式适应度函数计算每个鲸群个体的适应度值,找到并保存当前群体中最佳鲸群 步骤5t=t+1,更新a,A,C,l,p 步骤6 当p<0.5且|A|<1,利用(15)式更新当前鲸群个体的空间位置;若p<0.5且|A|≥1,则从当前群体中随机选择鲸群个体位置X(t)rand,并利用(20)式更新当前鲸群个体的空间位置 步骤7 若p≥0.5时,利用(19)式更新当前群体个体的空间位置 步骤8 利用(23)式适应度函数计算每个鲸群个体的适应度值,找到并保存当前群体中的最佳鲸群个体,判断算法是否满足终止条件,若满足输出最佳空域基准点;否则,令t=t+1,重复执行步骤5~7。 步骤9 根据飞行误差,确定最大偏移航线以及空域边界 步骤10 采用遍历法(本文采取1°间隔进行搜索),根据(14)式选择最佳干扰航线航向。 步骤11 输出干扰空域 图3 模型求解步骤 假设敌方4部探测雷达的坐标分别为(119.6,180.1)、(205.2,120)、(209.8,245.3)、(344.9,150);突防飞机完成任务后,按原航线返回,具体如图2所示。图中X轴和Y轴边界为预警机的指挥控制区域。为了简化计算,假定每部雷达的工作方式相同,频段不同、电子干扰飞机的飞行参数相同,频段不同,即一个干扰空域仅能干扰一个目标雷达。雷达的威胁参数和干扰机的参数具体为:Pt=120 kW,Gt=33 dB,θ0.5=2°,σ=1 m2,k=0.04,Pj=100 kW,Gj=30 dB,γj=0.5,Kj=2,V=300 km/h,γ=20°,N=106根。突防战机的飞行速度为1 200 km/h,人为误差概率为0.95,风速为23 m/s。 任务分析:为执行特定的作战任务,我方突防战机需要穿越敌防空雷达探测区,从图2可以看出,如果要使攻击任务完成需对雷达1、雷达2、雷达3进行干扰。 仿真1 分别用WOA算法和Tent混沌序列的WOA算法对进行仿真,初始参数设置如下:D=6,初始种群个数为50,最大迭代次数为100,b=1,λ1=0.6,λ2=0.4。在Matlab2014a软件上,进行50次运算,取其平均值可得图4的进化曲线对比和图5的每次运行程序所需时间,得到空域规划态势图(见图6)以及空域的具体参数,如表1所示。 表1 仿真1空域参数表 图4 迭代次数曲线 图5 算法运行时间 由图4可知使用Tent混沌序列进行初始化的WOA(TWOA)在开始时其适应度值小于WOA,这是由于混沌序列具有遍历性,后续阶段其寻优速度加快,最终所得到最大适应度函数值大于WOA的寻优值,表明TWOA比WOA寻优性能强,陷入局部最优的概率小。采用TWOA算法进行寻优所需的平均时间为4.481 086 38 s,表明算法的计算量不大、复杂度不高。采用WOA算法进行寻优所需的平均时间为4.474 562 28 s,二者相差的时间为6.524 1×10-3s,差别非常之小,随着计算机性能的进一步提升,这种差距会更加缩短,因而可以接受。 图6 仿真1空域规划方案 由仿真图6可知,按照表1所给定的参数对空域进行规划,突防飞机能够按预定航线对目标1和目标2进行攻击,可保证其距离各部被干扰雷达探测边界最近处有5.02 km,最远处可达32.96 km,说明该规划方案是有效的,能够保证作战飞机顺利完成对目标1和目标2的攻击任务,同时也表明按照本文所建模型对干扰空域进行规划,能够满足实际作战的要求,证明了该定量化的模型是科学、有效的。 仿真2 TWOA算法对进行仿真,初始参数设置如下:D=6,初始种群个数为50,最大迭代次数为100,b=1,λ1=0.8,λ2=0.2,得到空域规划方案图(见图7)以及空域的具体参数如表2所示。 表2 仿真2空域参数表 图7 仿真2空域规划方案 由表2的数据和图7的规划图可知,由于λ1取值的增大,即着重考虑干扰效果,仿真2所形成安全穿越区域较仿真1更为宽阔,各个干扰空域的所形成的最小宽度和最大宽度均有增加,例如干扰空域3在仿真2中的最小宽度比仿真1的最小宽度大5.75 km,在仿真2中的最大宽度比仿真1的最大宽度大7.24 km,同时各个空域所形成的宽度也更为均 匀。空域基准点与空域方向上,仿真1与仿真2所得的结果差异较大,方向的最大变化幅度为99°,这表明运用复合干扰模式规划空域时,其空域的配置更为灵活,这是由于复合干扰方式不需要像有源干扰那样要严格遵循干扰方向对准原则。这在需要规划多个空域时具有重大的意义,它能够在保证效果的前提下更为灵活的使用空域,对其它作战空域的限制性较小,使空域资源得到更为充分的利用。 为了有效解决单一有源干扰和无源干扰对新式雷达干扰效果差的问题,本文提出了一种复合干扰的方法,该种干扰方式对干扰机的有效辐射功率及箔条云的有效散射面积的要求较高,而且实施的距离与支援目标密切相关,继而对该种干扰方式进行了空域规划,同时得到了只要满足该种干扰方式的实施条件,其空域规划更为灵活,能够对其它空域产生较小的限制,使得在对多个军事空域进行规划时,该种干扰方式更具有优越性。2.2 箔条散射截面
2.3 效能分析
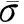
3 模型建立
3.1 问题描述

3.2 模型建立
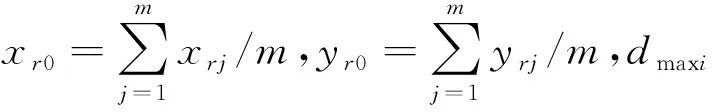
4 改进鲸群算法的模型求解
4.1 鲸群优化算法
4.2 改进策略
4.3 求解步骤
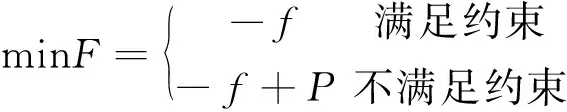
5 仿真分析


6 结 论
