含有时滞控制的准零刚度隔振器的隔振性能研究

李东海, 赵寿根, 何玉金, 李涛

(北京航空航天大学 航空科学与工程学院, 北京 100191)

振动隔离是解决工程振动问题的重要手段。在目前大量的工程实际中，普遍采用线性隔振器。由线性隔振理论可知，当系统的激励频率与隔振器的固有频率之比大于1.414时才具有隔振性能。对于一些精密仪器而言，如航天器上的光学元件，低频振动对其精度影响更大。如采用线性隔振措施，势必要降低隔振器的刚度从而实现低频隔振。这也会造成隔振器的静态稳定性降低。理想的情况是隔振器具有较高的静态刚度来保证静态负载能力，并且具有较低的动态刚度来增大隔振频率范围。高静态刚度低动态刚度(high-static-low-dynamic-stiffness,HSLDS)特性可以通过非线性结构来实现[1]。Ibrahim[2]综述了非线性隔振器的发展，表明非线性隔振是一个十分活跃的领域。Liu等[3]在其综述中也详细地阐述了非线性隔振器在微振动隔离领域的应用。Yang等[4]研究了带有负刚度机构的非线性隔振系统的动力学行为。研究表明增加负刚度机构能极大地扩展隔振频带，使系统具有更好的隔振性能。Shaw等[5]用双稳板设计了一种轻且有效的高静态低动态刚度(HSLDS)的隔振系统，用实验的方法证明其比等价的线性系统具有更大的隔振区域以及更低的固有频率。彭献等[6]采用连杆机构作为负刚度调节机构，研究了一种准零刚度隔振器的设计方法。Zhang等[7]将欧拉压杆作为负刚度调节机构，设计了正负刚度并联的隔振系统，不但显著降低了隔振系统的固有频率,同时也改善了系统的阻尼特性。徐道临等[8]设计一款屈曲板型准零刚度隔振器,该隔振器由竖直的橡胶垫和屈曲的弹簧钢板组合而成。并针对承载质量的变化会影响隔振器性能的问题,设计了具有准零刚度特性的可调式非线性气动隔振器[9]。刘兴天等[10]提出具有负刚度特性的欧拉屈曲梁结构并分析其静态特性。Carrella等[11-14]和王勇等[15]利用斜置弹簧产生负刚度特性，并与正刚度弹簧相并联组成准零刚度隔振器。张月英[16]在有关非线性隔振系统设计理论的基础上，设计并验证了一种由正负刚度并联组合得到准零刚度隔振器。Xu等[17]利用电磁弹簧作为负刚度元件，设计了一种准零刚度隔振器，该新型隔振器的隔振性能，尤其在低频区域，超过了等价的线性隔振器。闫建[18]基于屈曲状态下工作的欧拉梁能够提供负刚度的原理,设计了一种将欧拉梁与线性弹簧并联的低频隔振器,使其对低频振动具有良好的抑制效果。针对大型车载光电设备0～20 Hz低频段振动,基于准零刚度系统隔振原理,杜宁等[19]提出了一种新的低频水平方向隔振方法。Ishida等[20]提出了一种基于一种具有扭转屈曲模式可折叠圆筒的准零刚度隔振器。由于准零刚度具有高静态刚度低动态刚度，可以有效地克服传统非线性隔振器增加隔振频率范围和保证静态承载力之间的矛盾，近年来，针对准零刚度隔振器的研究变得越来越热门。

准零刚度隔振器有着线性隔振器不可比拟的优点，但是相比线性隔振器而言，其共振峰值依然过大；由于准零刚度隔振器的固有非线性，所以会造成系统的跳跃现象，这种不稳定性是一种不安全因素，所以在工程实际应用中不期望其出现。因此为了获得更好的隔振性能，开展准零刚度隔振器的主动控制策略的研究就显得十分必要。准零刚度隔振器的动力学特性方程可以用具有三次非线性项的Duffing振子模型来描述[1,21-24]。目前针对准零刚度隔振器的主动控制研究相对较少，但是许多学者开展了对Duffing振子和吸振器的主动研究[25-28]。通过时滞控制可以有效地抑制传递到敏感元件上的振动。但是针对准零刚度隔振器的时滞控制研究相对较少，本文在之前的研究基础上，对准零刚度隔振器施加线性位移时滞控制，在力激励的情况下，利用平均法得到了准零刚度隔振器的动力学响应，在此基础上，分析了时滞控制参数对准零刚度隔振器的力传递率的影响。

1 准零刚度隔振器动态响应

1.1 准零刚度隔振器

本文采用2个斜置弹簧作为负刚度元件与竖直的正刚度弹簧相并联形成单自由度的准零刚度隔振器[1,13]。对其进行线性时滞位移主动控制的结构模型如图1所示。

图1 准零刚度隔振器线性位移时滞控制结构示意图

在工作状态，斜置弹簧处于水平位置并达到静平衡点处[11,13]，其长度为l。自由状态时,距离静平衡位置的距离为xs;x为负载质量m从静平衡位置开始的位移。斜置弹簧的原长为l0。斜置弹簧的刚度为kh,垂直弹簧的刚度为kv,假设系统的阻尼为线性阻尼,阻尼系数为c,控制刚度为kc,反馈信号为系统的线性位移x;f为负载质量m受到的外界激励力。

1.2 简谐力作用下隔振器的响应

准零刚度隔振器线性位移时滞控制结构示意图如图1所示。为了建模的简便性,先考虑无控制系统的动力学特性。利用拉格朗日方程可以建立准零刚度隔振器在简谐力激励下的动力学方程。隔振器的动能为

(1)

现设静平衡位置为系统的势能零点,则该系统的总势能为

(2)

拉格朗日函数可以表示为

(3)

拉格朗日方程表示为

(4)

式中,Fe(t)=Fcos(ωt)为隔振器受到的简谐激励力,t为时间,ω为简谐激励力的频率。联立(3)式和(4)式可得到隔振器的动力学方程

(5)

引入无量纲参数,可对(5)式无量纲化,得到隔振器的无量纲动力学方程

(6)

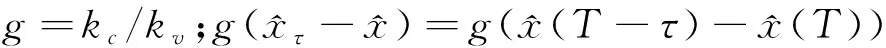
(7)

当隔振器的位移相对初始位移为小量时,可以将系统的动力学方程在静平衡点处泰勒展开并保留三次精度得到

(8)

(9)

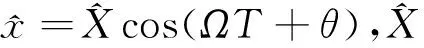
(10)

式中

将ΩT+θ在0～2π之间取平均值得到

(11)

(12)

利用sin2θ+cos2θ=1可以得到系统的幅频响应特性

(13)

相频特性方程为

(14)

该受时滞控制的准零刚度隔振器的更为详细的动态特性研究及稳定性分析见文献[29],为节省篇幅,本文将不再赘述。

2 准零刚度隔振器力传递率

2.1 力传递率

(15)

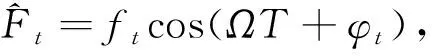
(16)

一般地,力传递率TF定义为传递到基础上的载荷的幅值ft和激励幅值fe的比值。即

(17)

将(13)式和(16)式代入(17)式可得含有时滞线性位移的准零刚度隔振器的力传递率为

(18)

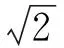
图2a)中右边的曲线簇为有线性位移时滞控制的等效线性隔振器的力传递率曲线,左边曲线簇是含有线性位移时滞控制的准零刚度隔振器的力传递率曲线。对比准零刚度隔振器的力传递率曲线和其等效线性隔振器的力传递率曲线可知,当外界激励力为极限载荷时,当频率比Ω<1时,尽管准零刚度隔振器的力传递率比其等效线性隔振器的力传递率大,但是依然可以看出来,准零刚度隔振器的隔振频率带依然比线性隔振器的频率带宽,而当激励力的幅值小于极限载荷时,准零刚度隔振器的隔振频带会更宽,其隔振性能的优越性越明显,该方面的论述详见参考文献[1]。

当有线性位移时滞控制时,准零刚度隔振器低频段的力传递特性相比无时滞控制时的力传递率降低,且传递率峰值也明显地降低,由此可以看出时滞控制的阻尼效应,且当时滞参数τ给定在合适范围内,随着控制增益g的增加,其等效阻尼ξeq越大[29],故其传递率峰值随着g的增加而降低,且当等效阻尼越大时,其高频段的力传递率越大。相比无控制系统,有时滞控制情况下的隔振频率较大,且随着控制增益的增大有增大的趋势。对比有控制的准零刚度隔振器与其等效的线性隔振器的力传递特性,可以清晰地看到有时滞控制的准零刚度隔振器的力传递特性要好于等效线性隔振器,尤其是在高频段内,准零刚度隔振器的力传递率有很大程度降低。在图2中也可以看出时滞控制对系统线性刚度的影响,其表现在力传递率曲线的向右弯曲开始频率右移,原因在于所选择的时滞参数和控制增益造成了系统的线性刚度系数增加。尽管如此,有时滞控制的准零刚度隔振器的隔振性能依然好于无控制时的隔振器,且可以增加系统的静态鲁棒性。

图2b)中外部激励力为极限载荷。在图中,靠右的曲线簇为等效线性隔振器的力传递率特性曲线,左边的曲线簇是准零刚度隔振器的力传递率特性曲线。准零刚度隔振器及其等效线性隔振器的力传递率特性曲线随着时滞参数τ的变化规律和图2a)中的变化规律类似。由此可见,对准零刚度隔振器施加线性位移时滞控制不仅可以有效地改善系统的力传递率特性,而且可以增加系统的静态鲁棒性。

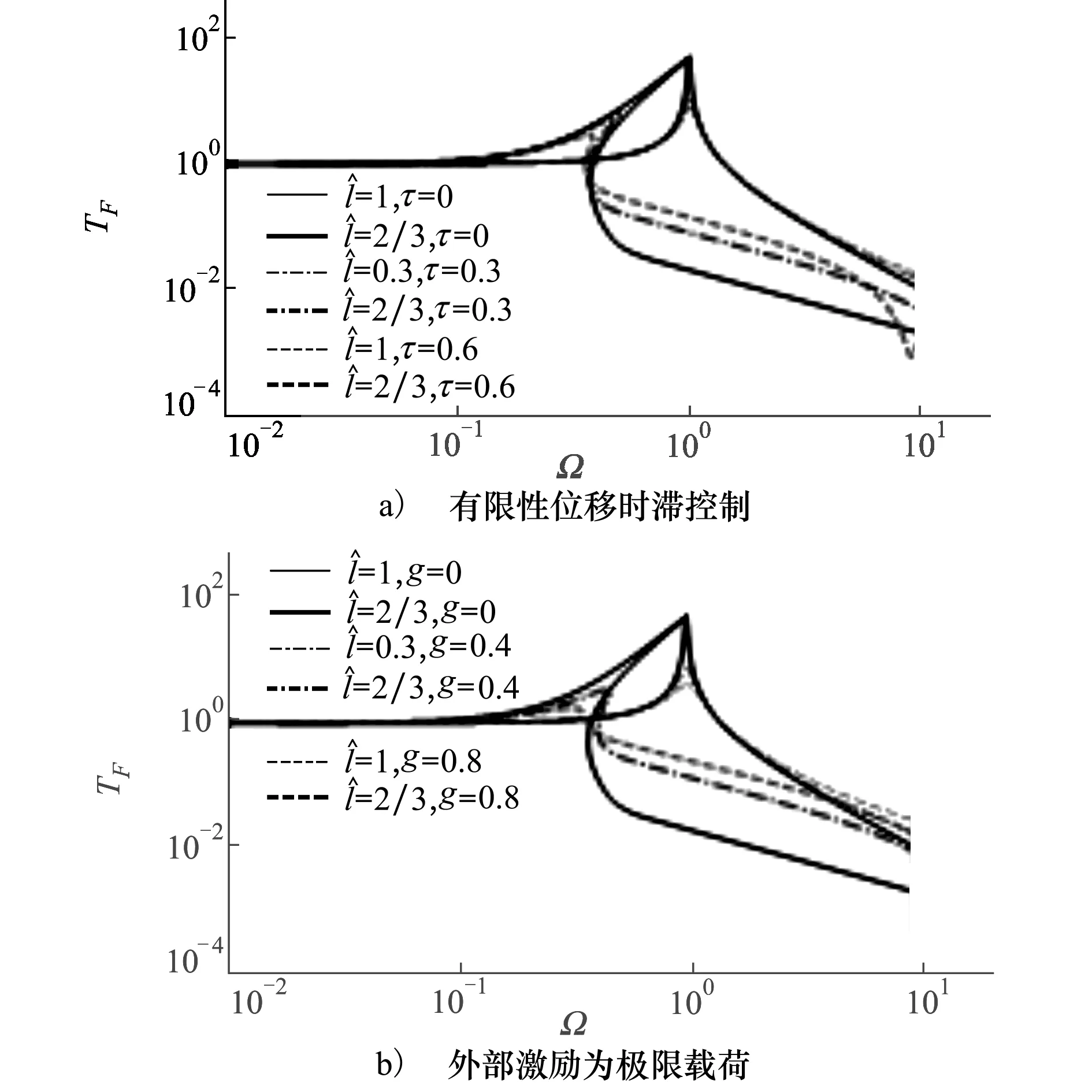
图2 含有线性位移时滞控制的准零刚度隔振器力传递率曲线

2.2 传递率峰值

准零刚度隔振器的传递率峰值发生在系统的位移响应最大时[1],而当系统的位移响应的相位和外部激励力的相位相差-π/2时,系统位移响应最大[22]。因此可由(12)式得到系统的最大响应位移为

(19)

式中,Ωmax表示当位移响应最大时所对应的频率比。可以得到其对应的外界激励力的幅值fe为

fe=2(gsin(Ωmaxτ)+2ξ)·

(20)

此时隔振器的最大位移响应为

(21)

将(21)式代入(18)式中就可以得得到当系统发生最大位移响应时的频率为Ωmax时的传递率峰值。

(22)

考虑到准零刚度隔振器的特性,故其传递率峰值所对应的频率比不能大于1,因为若大于1时,则隔振性能不如等价的线性隔振器。所以,令Ωmax=1可得到所允许施加到隔振器上的最大外界力激励的幅值fe|Ωmax=1为

(23)

此时隔振器的最大响应位移为

(24)

将(24)式代入(22)中可以得到当发生最大位移响应时的频率为Ωmax=1时准零刚度隔振器传递率峰值TF|Ωmax=1为

(25)

图3a)所示是当时滞参数τ=π/6时,准零刚度隔振器在不同控制增益参数g下的力传递率峰值。当g=0时表示无控制,由图3a)可知当控制参数选择在合适范围内时,有控制时系统的力传递峰值比无控制时小,且当时滞参数一定时,随着控制增益的增加,系统的力传递率峰值相应减小。且力传递率峰值的大小随着共振频率的增加而增大。由图3a)可知时滞控制可以有效地抑制准零刚度隔振器的力传递率峰值,因而可以大幅地提高隔振器的隔振性能。图3b)所示是当控制增益参数g=0.4时,准零刚度隔振器在不同时滞参数τ下的力传递率峰值。图3b)中曲线的变化规律与图3a)中的变化规律类似,当控制增益一定且时滞参数在一定范围内时,隔振器的力传递率峰值随着时滞参数的增加而增加。说明时滞控制可以有效地抑制系统的力传递率峰值,大幅地提高系统的隔振性能。

图时准零刚度隔振器力传递率峰值曲线

图4为受控准零刚度隔振器在不同简谐力激励下的传递率曲线。不同激励力的传递率峰值均在传递率峰值曲线上。值得注意的是,当力激励幅值大约为不受控系统的临界载荷的6倍时,最大传递率发生在频率比为1处。意味受控系统相比不受控系统能够承受更大的激励力,因此能够适应更加极端的工作环境。

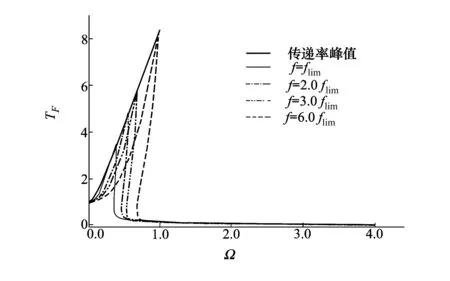
图4 不同简谐力激励下的受控准零刚度隔振器的力传递率

3 算例分析

根据文献[30]中实测得到的某飞轮引起的径向扰振力为本文中的准零刚度隔振器所受到的外界激励,其具体表达式为

(26)

其无量纲化的表达形式为

(27)

隔振器和飞轮的参数取值如表1所示。将各参数以及(27)式带入(8)式并联立(15)式可得到传递到基础上的无量纲力。图5为含有时滞控制的准零刚度隔振器对该飞轮扰振力的隔振效果。从图中可以得知,传递到基础上的力的幅值约为飞轮扰振力的10-4倍。从曲线结果可以看出由于准零刚度隔振器的固有频率较低,对具有较高频的飞轮扰振力具有良好的隔振效果。

表1 计算参数取值

图5 含有时滞控制的准零刚度隔振器对飞轮扰振力隔振效果

4 结 论

本文研究了带有线性位移时滞控制的三弹簧准零刚度隔振器在简谐力激励下的隔振性能。结果表明,相比线性隔振器,准零刚度隔振器的隔振频率带更宽;而增加时滞控制可以进一步地拓宽隔振带宽,改善低频带系统的隔振性能;且在高频段受控系统的力传递率要比不受控系统的力传递率小,表明增加时滞控制不仅可以改善低频段隔振性能,而且系统的高频段隔振性能也会得到改善。最后给出了力传递率峰值的理论结果,不仅表明有时滞控制的系统的力传递率峰值得到了有效地抑制,而且增加时滞控制可以使隔振器适应更加极端的工作环境。