不确定条件下无人机编队在线协同轨迹规划研究

王渊, 魏政磊, 黄长强, 黄汉桥,2, 赵克新, 李聪

(1.空军工程大学 航空工程学院, 陕西 西安 710038; 2.西北工业大学 无人系统技术研究院, 陕西 西安 710072)

未来战场环境日渐复杂,无人作战飞机(unmanned combat aerial vehicle,UCAV)的单机模式难以应对突发事件和多变的环境,无人机编队可以通过能力互补与行动协调,提高完成任务的质量,缩短执行时间,并且降低风险。在实际作战任务过程中,UCAV面临的战场态势和任务目标不断地随着时间变化,使得多UCAV协同作战变得非常复杂。

目前,作为协同作战关键技术之一,UCAV编队协同轨迹规划成为国内外研究的热点[1]。针对协同轨迹规划问题,文献[2]采用空间模糊集建立三维多无人机协同航迹规划模型;文献[3]提出了一种基于协同非支配排序进化算法的航迹规划方法;也可以采用其他智能算法对协同航迹规划问题求解,比如蚁群算法[4]、遗传算法[5]、病毒搜索算法[6]等。关于无人机协同轨迹规划的文献很多,但是大多数没有考虑到无人机的平台运动特性或者编队的相对运动特性[7],得到的航迹是不可执行的。针对具有运动特性的轨迹规划问题,文献[8]采用了自适应伪谱法并对UCAV低可探测攻击轨迹进行仿真;文献[9]对多机轨迹规划凸化与离散化,并提出了基于罚函数序列的凸规划方法。在实际的无人机协同任务执行过程中,可能要面临战场环境和任务需求以及任务信息的变化,导致现有的轨迹对实时环境不适应[10-11]。文献[12]采用滚动时域策略和Gauss伪谱法解决在线攻击轨迹决策问题;文献[13]提出了基于随机搜索树的轨迹重规划方法。同时,相关文献中的协同轨迹规划模型同时或部分存在以下问题:①未考虑威胁环境变化或者任务变化[14];②未考虑相对运动特性[15];③未详细考虑无人机运动学/动力学模型[16]。

针对以上存在的问题,提出了基于hp自适应伪谱法(hp adaptive pseudospectral method,hpAPM)的编队在线协同轨迹规划方法。首先通过分析无人机编队攻击过程,提出了多约束编队轨迹规划模型;针对在线协同轨迹规划,在优化时间片内采用了hp自适应伪谱法进行局部重规划;最后进行了仿真验证。

1 无人机编队攻击过程分析

无人作战飞机编队协同攻击轨迹规划是指多架无人机编队根据飞行任务的需求,设计出编队从起点到目标终点,再到协同离开战场的整体最优飞行轨迹,并且使得综合代价最小,同时要求满足无人机编队机动性能约束[17]。现实中的UCAV编队攻击过程可能存在诸多不确定条件:①战场环境的变化,如发现新的威胁(突发威胁使原有的飞行轨迹受到较大的安全威胁);②任务目标的动态性,如任务目标位置机动(目标的大机动使预先规划轨迹偏离目标较远)与任务目标增减(原有的任务目标取消与新增新的更加紧迫的任务);③其他因素,如UCAV系统误差与阵风影响[18]。当面临如上情况时,无人机编队轨迹需要重新规划或者在线局部调整。UCAV编队攻击过程如图1所示。

图1 UCAV编队攻击过程

编队的任务协同不仅仅包括时间协同,还包括了各个无人机的姿态、速度、高度等空间协同要素[19],如图2所示。本文假设由2架UCAV组成编队,2架UCAV分别是长机(Leader)与僚机(Follower)。在确认任务目标之后,总控台根据具体的任务信息与任务结构,将任务分配给各个UCAV;Leader根据分配的任务信息、感知的任务环境以及两机的相对位置、速度、角度,通过轨迹规划模块快速输出最优轨迹,最后将Leader的攻击轨迹参数发送到总控台和Follower;Follower再根据Leader的攻击轨迹参数得到本机的最优任务执行轨迹。Follower作为编队的一部分,既可以独自执行攻击任务,也可以配合Leader执行任务。

图2 UCAV编队协同要素分析

2 编队轨迹规划建模

2.1 参考坐标系的定义

参考坐标系的选择有好多种,比如地面坐标系、机体坐标系、速度坐标系等。本文除了涉及地面坐标系OXYZ外,还定义了UCAV质心运动的航迹坐标系作为编队的参考坐标系。定义如下:原点Od位于UCAV质心;OdXd始终与无人机的速度V的方向重合一致;OdZd在包含飞行速度V在内的铅垂平面内,飞行方向与OdXd垂直,并指向上方;OdYd则垂直与OdXdZd平面并指向右方。无人机质心相对于地面坐标系的运动则由航迹倾斜角γ、航迹偏角ψα、速度滚转角μ以及速度V确定,如图3所示。

图3 无人机运动参考坐标系

2.2 UCAV运动学/动力学模型

无人机采用的是质点运动模型,同时用考虑测力因素的动力学模型改进文献[20]中的模型,即得到UCAV单机运动学/动力学模型:

(1)

(2)

T=δTmax(vu,h)

(3)

(4)

(5)

式中,δ为油门位置,Tmax为最大可用推力,h为海拔高度;ρ为空气密度,S为UCAV横截面积;CD为阻力系数;CL为升力系数。

根据文献[21]中提到的飞行包线约束,建立UCAV的约束条件:

(6)

2.3 编队相对运动模型

UCAV编队过程中最重要的一点就是长机与僚机之间相对距离的保持,本文采用文献[15]中的编队相对运动模型,图4所表示的是在地面坐标系中长机与僚机位置矢量之间的关系。

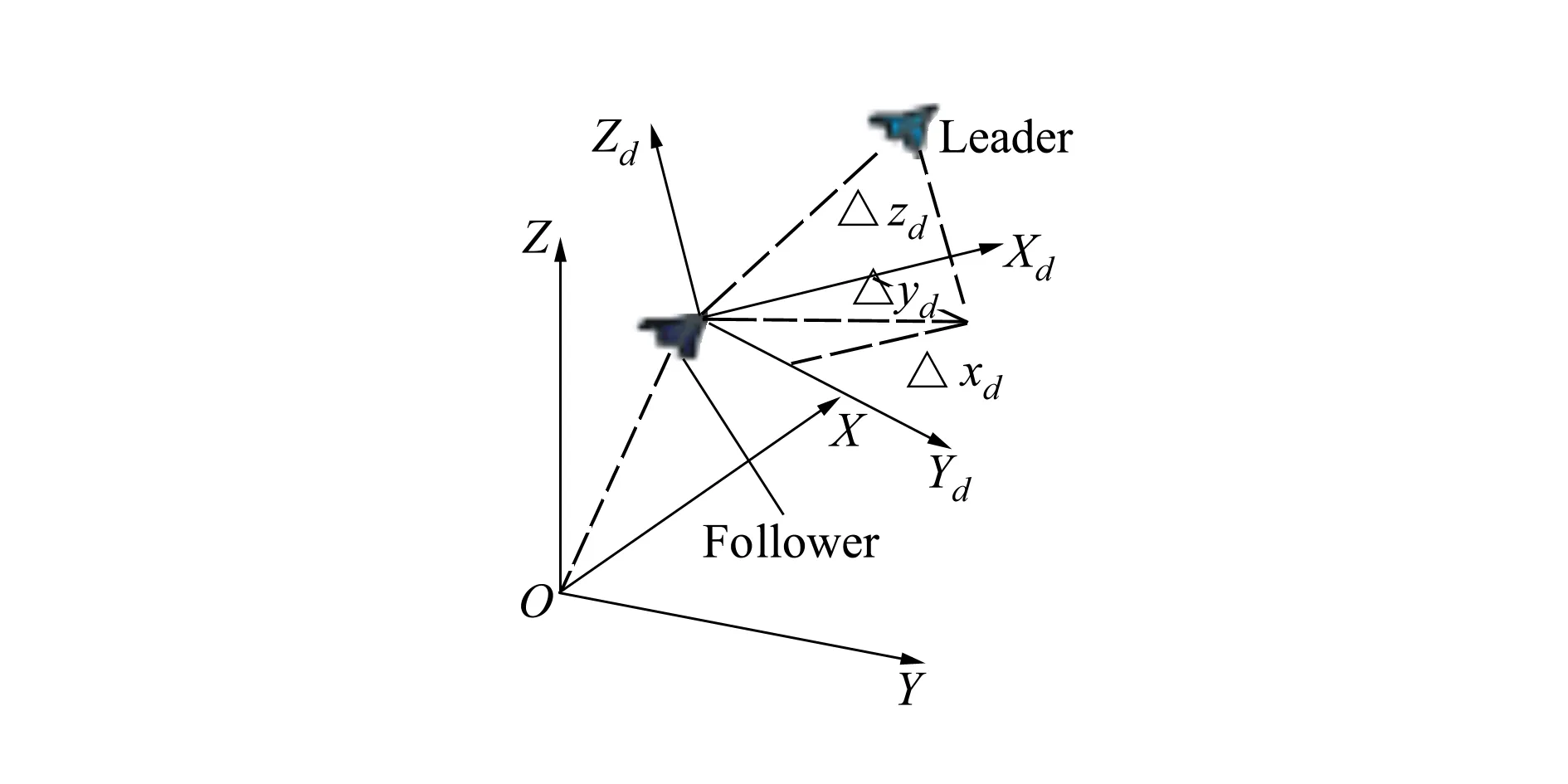
图4 编队成员之间的相对位置关系

(7)

通过公式(1)、公式(2)和公式(7)的联列,便可得到UCAV编队的运动学/动力学模型。

2.4 目标函数

UCAV编队轨迹规划不仅仅要考虑单机的轨迹规划约束条件[8],还包括UCAV之间的空间协同约束与时间协同约束。

对于UCAV编队间的空间约束,本文考虑的是碰撞约束,建立的目标函数是:

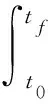
(8)

式中,Jcollision表示碰撞目标函数;t0和tf分别为初始时间和末段时间;ζ表示等效碰撞,当长机与僚机之间的距离Rd大于安全相对距离Rsafe时,ζ取值为0,否则为1。

对于协同时间约束,建立的目标函数为

(9)

式中,Jcooperatetime表示时间目标函数;ti为UCAV到达指定位置的时间;tic为UCAV到达指定位置的指令时间。

UCAV在执行任务过程中,会受到来自地面雷达与防空火力的威胁。对于UCAV受到的威胁模型,本文采用模型是文献[8]中的威胁矢量模型,那么威胁目标函数为

(10)

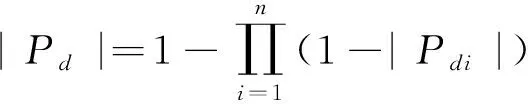
(11)

式中,Jthreat为威胁代价值;|Pd|表示联合防空系统探测概率的大小[20];|Pdi|为子系统的探测概率大小;n为联合防空系统子系统数量。

根据上面目标函数的分析和实际战场的需要,综合目标函数[12]为

(12)

式中,J为综合目标函数值;tf为编队完成任务时间终端,t0为编队执行任务初始时间;ω1+ω2+ω3+ω4=1,ω1,ω2,ω3和ω4分别为时间、威胁、等效碰撞次数、指令时间误差的权重系数。

3 UCAV轨迹在线规划方法

3.1 在线规划策略

不确定环境下的UCAV轨迹规划问题较为复杂,除了要考虑不断变化的约束环境,还要考虑选取收敛精度高、计算速度快的算法。针对这一问题,本文提出一种基于hp自适应伪谱法的在线轨迹规划算法,即首先对全局空间进行UCAV编队的离线轨迹规划,采用的方法是hp自适应伪谱法;然后根据实时的任务环境信息,取较少的Gauss节点,利用hp自适应伪谱法在线求解局部轨迹,如图5所示。

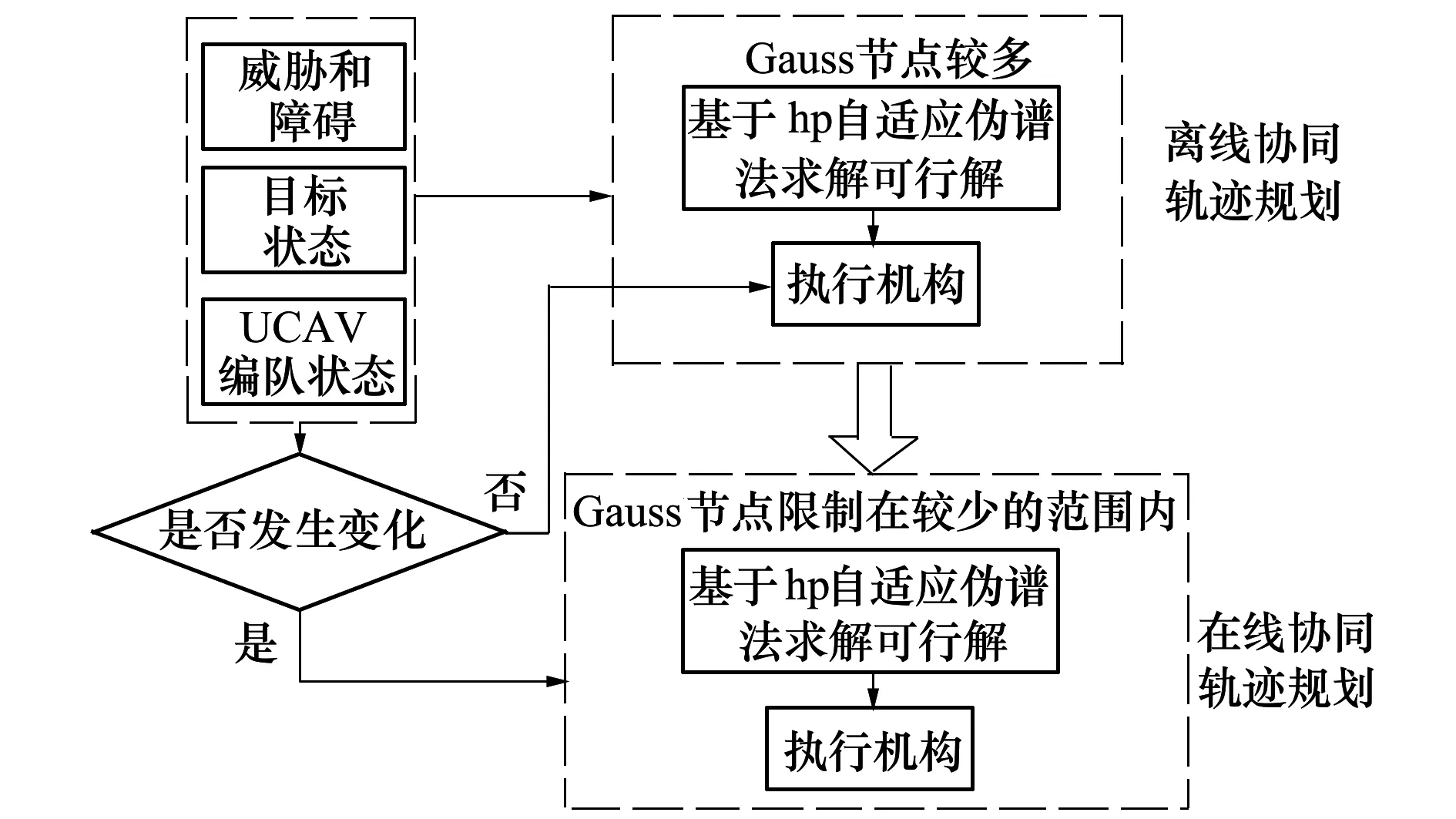
图5 在线轨迹规划策略

在线轨迹规划策略把整个任务过程划分为若干个相互迭代且不断向终点目标推进的优化时间片(这个时间片也称为优化区间或者滚动窗口),并根据任务环境的变化情况对局部轨迹进行调整或者重规划[11]。本文定义的轨迹重规划的触发事件(导致重规划的不确定条件)是:①突发威胁;②任务目标的改变(包括任务目标的机动与增减)。同时,本文采用文献[11]中的方法来设计重规划区域大小、轨迹起点位置以及终点位置;对于终点的状态变量,直接采用离线全局规划该位置点的状态变量。

在线轨迹规划步骤为:

step1 UCAV编队根据综合传感器实时上传的数据信息,判断轨迹重规划的触发事件是否发生,如果事件发生,则转step2;否则,根据离线轨迹继续执行任务,重复step1;

step2 UCAV编队根据突发威胁与任务目标变动情况,快速确定重规划区域大小、轨迹起始点位置;然后用hp自适应伪谱法求解重规划轨迹,转入step3;

step3 UCAV编队根据重规划轨迹执行任务,直到满足终止优化条件,否则装入step1。

3.2 基于hp自适应伪谱的轨迹优化算法

1) NPL构建

采用Gauss伪谱法求解连续最优控制问题的基本原理是:将状态变量和控制变量在一系列Gauss点上离散,并以这些离散点为节点构造Legendre插值多项式来逼近状态变量和控制变量。通过对全局插值多项式求导来近似状态变量对时间的导数,将微分方程约束转换为代数约束,性能指标的积分项由Gauss积分计算,终端状态也由初始状态和对右函数的积分获得。具体的转换如下[15]:

(1) 将最优控制问题的时间区间[t0,tf]转换到[-1,1],因此对时间变量t作如下的变换:

(13)

(2) 用全局插值多项式近似控制变量与状态变量。选取K阶LG点,即K阶Legendre多项式PK(τ)的根,其中

(14)

确定配点后,取K个LG点以及τ0=1作为离散节点,并将K+1个Legendre插值多项式Li(τ)(i=0,1,…,K)作为基函数来近似状态变量的时间历程,即

(15)

式中

(16)

(17)

(3) 离散条件下的终端状态约束为

(18)

(4) 动力学微分方程约束转换为代数约束,即

(19)

式中,微分矩阵D由下式确定:

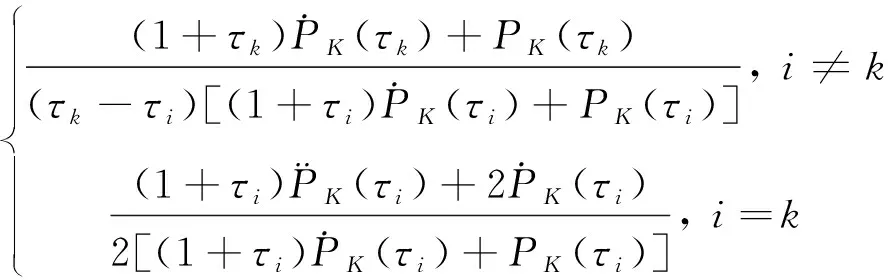
(20)

(5) 基于Gauss积分的近似性能指标函数

(21)

式中,Φ为非积分项指标;g为积分项指标的被积分项。

2) hp自适应策略

hp自适应伪谱法是一种结合有限元思想和经典伪谱法的最优控制方法,通过将整个时间区间划分为N个时间段,然后通过Gauss伪谱法对每个时间段进行离散化[22]。本文采用文献[22]中的hp自适应策略,其主要是根据每个时间段的曲率和约束方程的误差来调整时间段的数量和多项式的阶数,其中,p方法是增加一个时间段内的多项式阶数去更接近状态变量与控制变量,h方法是整个时间区域的时间段数来增加轨迹规划精度,曲率误差bk和约束方程误差ek分别表示为:

bk=Ck(Xk,Uk,τk,tk,tk-1)

(22)

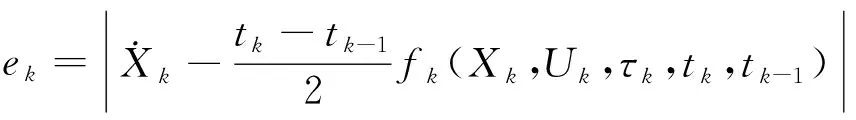
(23)

式中,如果bk和ek均小于规定的误差εd,则当前状态变量和控制变量为最优控制近似解;否则,采用文献[22]中的策略重新构造时间段与内部节点数量。

4 仿真结果及分析

4.1 任务环境想定

为验证方法的有效性与稳定性,针对经典双机编队的协同轨迹规划进行仿真实验。假设无人机编队在位置(20,20,0)km处发现一个目标,其中当前目标类型为地面固定目标;当前的威胁分别是雷达和防空导弹阵地,其分布情况如表1所示。

表1 威胁位置信息

威胁参数参考文献[8];UCAV的性能参数如表2所示,编队无人机任务开始状态与退出战场状态的仿真参数见文献[20]。UCAV武器为某型半主动激光制导导弹,其性能参数参考文献[20]。UCAV编队协同轨迹规划模型的目标函数各权重系数设置为:ω1=ω2=ω3=ω4=0.25。

表2 UCAV模型参数

[γmin,γmax]/(°)[αmin,αmax]/(°)[βmin,βmax]/(°)[μmin,μmax]/(°)Overload/gαminαmax]/(°)βminβmax]/(°)μminμmax]/(°)[-89,89][-10,30][-20,20][-75,75]≤6.8[-30,30][-10,10][-50,50]

本文采用Matlab 2014a进行仿真,运行环境为Inter(R)Core(TM)i5-3470处理器,操作系统为Windows7。

4.2 离线轨迹规划仿真分析

1) 离线轨迹规划仿真分析

为了验证基于hp自适应伪谱法协同轨迹规划的有效性,对该实验进行仿真,仿真结果与分析见后。

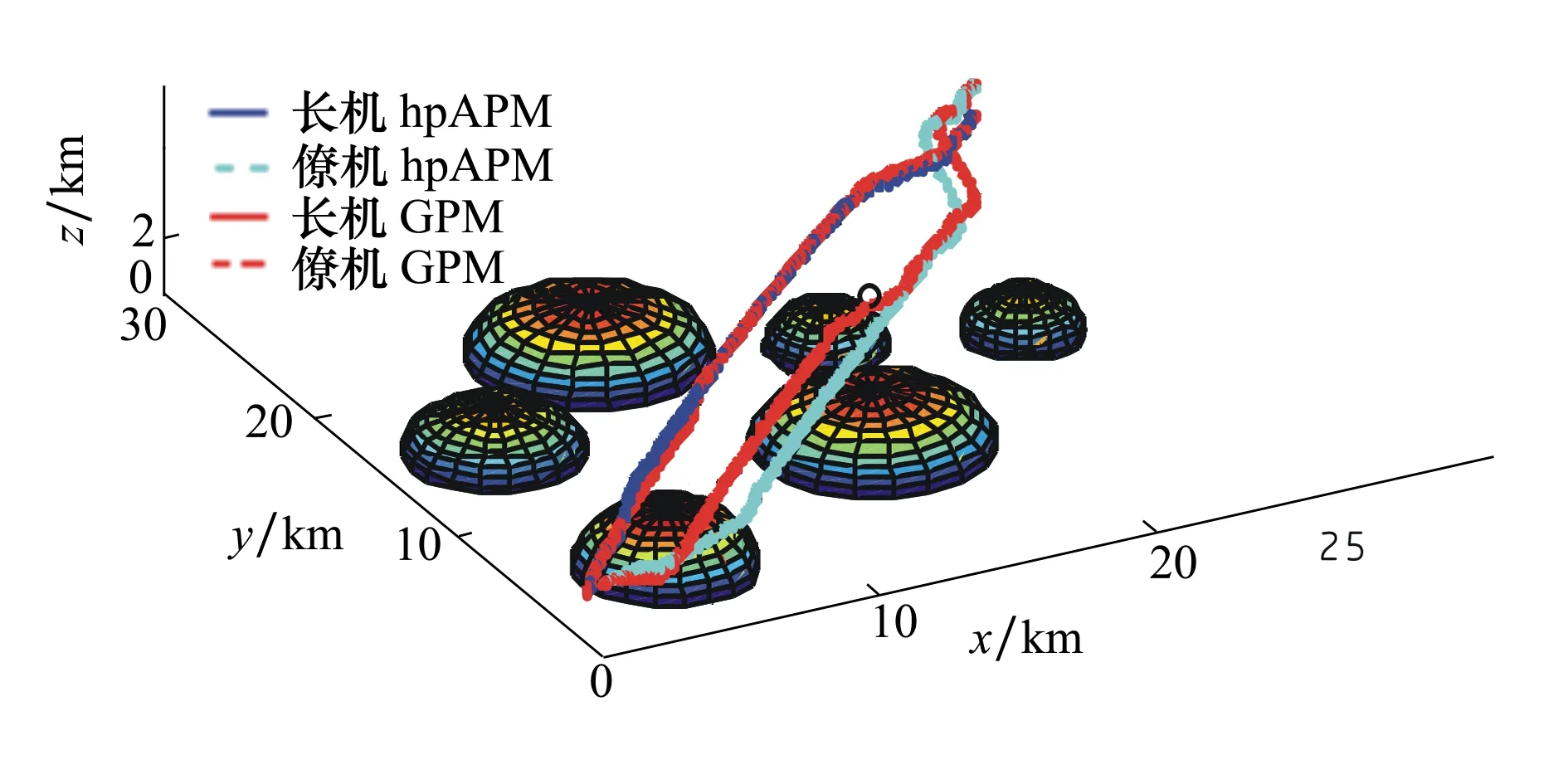
图6 编队轨迹图

图6为编队的二维轨迹与三维轨迹。从图中可以看出,UCAV并没有穿过威胁区,而是利用高度优势躲过威胁;所规划的轨迹是比较光滑的,符合飞行轨迹的真实性;另外一方面,基于hp自适应伪谱法的轨迹规划相对于基于GPM的离线轨迹规划更加光滑,规划精度更高。图9和图10中分别为编队离线轨迹规划的控制参数和状态参数变化曲线。从中可知,在整个轨迹规划过程中,编队的控制量都在设定的范围内,飞行姿态都能满足协同轨迹规划的约束条件;从图10d)中可知,长机在60 s的时候投放武器,去攻击目标。图11为UCAV编队成员间的相对距离变化曲线。从图可以看出,规划出的轨迹的等效碰撞次数为0,也就是满足不发生碰撞的条件;同时,随着任务执行时间的增加,长机与僚机之间的相对距离先增加后减小,首先因为长机与僚机的任务不同,其次攻击任务完成,编队返回。整个编队基于hp自适应伪谱法的协同轨迹规划时间为138.66 s,目标函数值为193.64;而基于GPM的规划时间为189.36 s,目标函数值为204.41。

综合上面仿真实验的分析,基于hp自适应伪谱法的编队协同轨迹规划是可行有效的,并且与基于GPM的轨迹规划相比较,其规划时间更短,规划精度更高。

2) 基于不同节点的离线轨迹规划仿真分析

为了验证该方法关于节点参数的求解稳定性,在不同节点范围内进行仿真实验。根据hp自适应策略的定义,每个时间段内的节点被控制到一定的范围内,分别选取4个范围进行仿真,得到表3与图7。

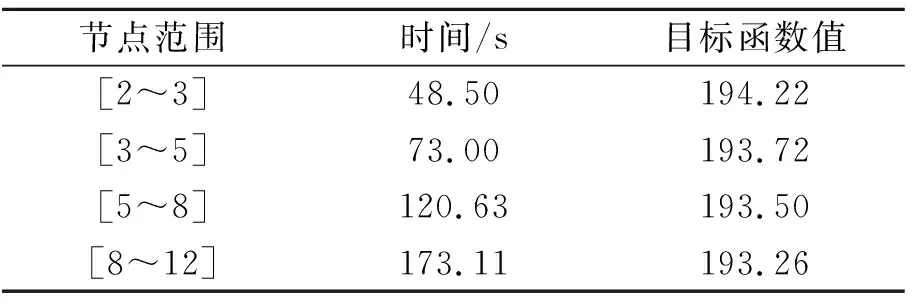
表3 不同节点范围内的规划结果

表3为不同节点范围下的轨迹规划时间和目标函数,随着节点范围内节点数增加,规划时间增大,规划目标函数值反而减小。图7为4个节点范围内的编队三维空间轨迹图,随着节点范围内节点数增加,规划轨迹变得更加精细。综上分析,节点数增加使轨迹规划时间变长,但是精度越高。

图7 不同节点范围下的编队轨迹

4.3 在线轨迹规划仿真分析

1) 基于突发威胁的在线轨迹规划仿真分析

为了验证在线轨迹规划方法的可行性与有效性,对基于突发威胁的在线轨迹规划进行仿真实验。UCAV编队在10 s时探测到新的威胁SAM-B,其位置为(10,7,0)km;同时,根据在线轨迹规划策略,对不满足飞行约束的轨迹进行重规划,重规划的区域要满足局部规划运行时间,因而选择25 s到45 s进行规划,并且选择节点范围[3～5]。图8为突发威胁环境下的编队轨迹规划,包括原先轨迹，基于hpAPM的局部重规划轨迹和基于GPM的重规划轨迹。从图中可以看出，当原先轨迹不满足威胁约束时，重规划轨迹则避开威胁。

图8 编队重规划轨迹

图9和图10为编队重规划前后的控制参数和状态参数变化曲线,其中重规划各参数变化曲线满足协同轨迹规划约束条件。图11为突发威胁段编队成员之间相对距离变化曲线,其大于最小安全距离。基于hpAPM的重规划时间为14.74 s,目标函数值为56.34,而基于GPM的重规划时间为23.50 s,超过规划区的时域时间,目标函数值为61.32,因此基于hpAPM的在线轨迹规划比基于GPM的轨迹规划结果更好。

图9 编队控制参数变化曲线

图10 编队状态参数变化曲线

图11 相对距离变化曲线

图12 编队重规划轨迹

图13 油门变化曲线

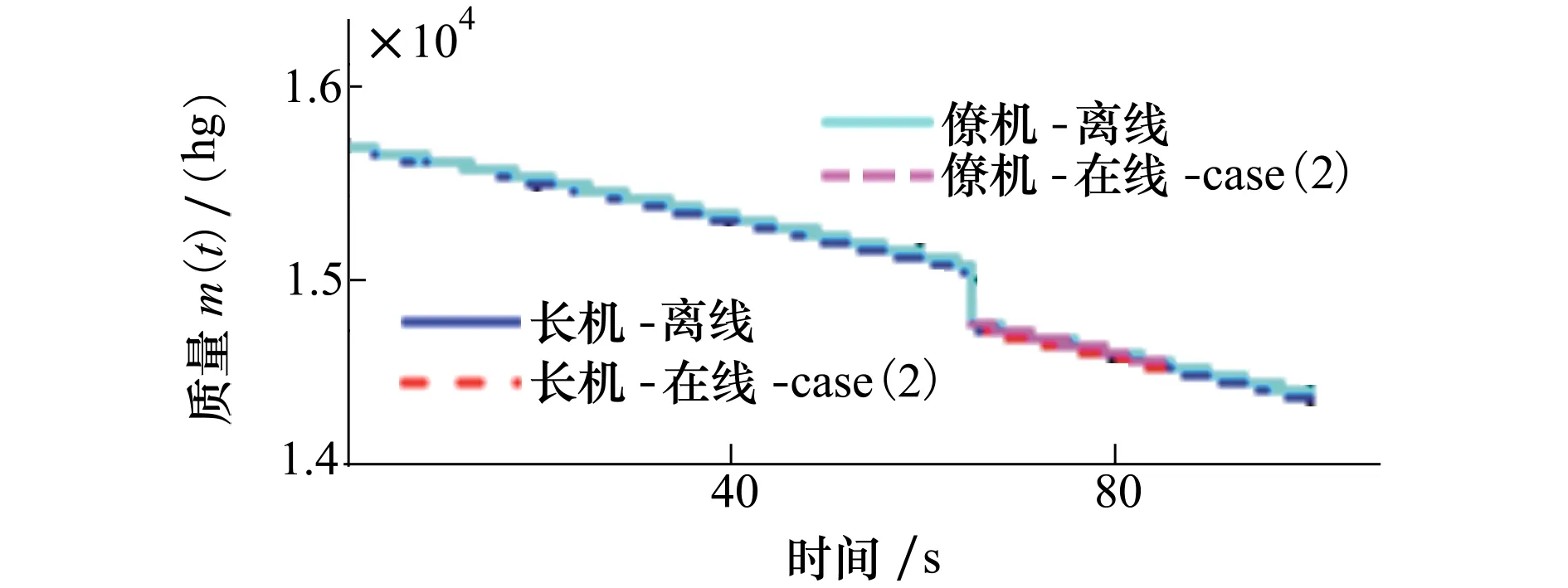
图14 质量变化曲线

2) 基于新增任务的在线轨迹规划仿真分析

为了验证在线轨迹规划方法的求解稳定性,对基于新增任务的在线轨迹规划进行仿真实验。在50 s时刻,编队探测到新增任务和新的威胁;新增的任务由长机执行,其目标位置为(17,22,0)km;原先的任务目标位置发生机动,从原先的位置点(20,20,0)km机动到位置点(20,18.5,0)km;同时,探测到新的威胁SAM-B,其位置为(19.5,21,0)km;根据在线轨迹规划策略,重规划的区域要满足局部规划运行时间,因而选择65 s到85 s进行规划,并且选择节点范围[3-5]。图12为新增任务环境下的编队轨迹规划,包括基于hpAPM的局部重规划轨迹和基于GPM的重规划轨迹;从图可以看出,当原先轨迹不满足威胁约束时,重规划轨迹则避开威胁。图9a)～c)和图13为编队重规划前后的控制参数变化曲线,图10a)～c)、e)～g)和图14为编队重规划前后的状态参数变化曲线,同时满足协同轨迹规划约束。图11为重规划编队成员之间的相对距离变化曲线,其满足不发生碰撞约束条件。基于hpAPM重规划时间为14.67 s,目标函数值为56.37,而基于GPM重规划时间为24.01 s,目标函数值为66.84,结果说明基于hpAPM重规划方法更好。

5 结 论

本文针对无人机编队在线协同轨迹规划问题进行了研究。根据编队协同轨迹规划的任务特点,基于UCAV运动学/动力学模型,结合相对运动方程,建立了编队协同对地攻击轨迹规划模型;以编队代价为出发点,考虑了单机威胁代、编队成员间威胁以及执行指令时间误差,提出了协同轨迹规划的目标函数;根据在线协同轨迹规划的复杂实时环境特点,通过局部重规划策略,设计了一种基于hp自适应伪谱法的在线轨迹规划算法;最后,对本文所设计的基于hp自适应伪谱法的协同轨迹规划从离线与在线2种情况进行仿真验证。仿真结果表明,该方法解算的轨迹能满足设定的约束条件,有效地解决了在线协同轨迹规划问题。