关于“圆在滚动中的自转圈数”问题的探讨

2019-01-03王东升

中国数学教育（初中版） 2018年12期

王东升

（辽宁省阜新市教师进修学院）

在现行各版本初中数学教材、多地的中考数学试题，乃至数学竞赛题中，都出现过“圆在无滑动的滚动中自转圈数”的问题.概括起来，此问题从形式上可分为三类：（1）圆在直线上滚动，如例1；（2）圆在多边形（折线）上滚动，如例2；（3）圆在圆周（曲线）上滚动，如例3.

要解决好这类问题，首先要对什么是“圆自转一圈”有一个正确的认识（这对第（3）类问题的解决显得尤为重要）.所谓“圆自转一圈”，从图形特征上看，可以认为是参照元素重回原位置.如果把这一说法数学化，则如由图1到图2，圆的半径OA在圆自转后回到原位置O′A′，OA∥O′A′，且方向相同. 为什么要强调方向相同呢？如图1（3）所示的圆，其中的半径与起始位置的半径所在直线也是平行的，但此时圆并非自转1圈，事实上，只转半圈而已.就圆周上的参照点A来说，它绕圆心旋转360∘°时圆自转一圈.

图1

图2

那么，每种类型的问题的规律如何呢？下面进行分类探讨.

一、圆在直线上滚动

例1如图3，一个半径为2 cm的圆，在10 cm的线段AB上滚动（无滑动，下同），由点A到点B滚动结束时，⊙O自转了几圈？

图3

分析：如图4，设⊙O的起初位置为⊙O1，滚动一周后的位置为⊙O2.直线与两圆相切，切点为点A，A′，且O1A∥O2A′，则线段O1O2=AA′为⊙O的周长.此时，⊙O恰好自转一圈，即圆的自转圈数（其中，l为圆在直线上滚动的距离，c为圆周长）.

图4

解：.

二、圆在多边形（折线）上滚动

例2如图5，一个半径为2 cm的圆，在△ABC的外部，沿三角形的边滚动一周，其中AB=5 cm，BC=6 cm，CA=7 cm.滚动结束时，⊙O自转了几圈？

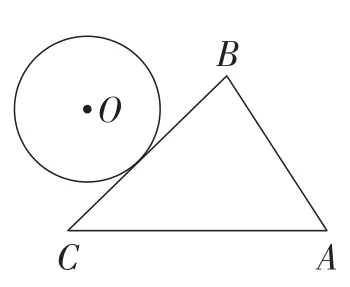
图5

分析：理解圆沿三角形的边滚动一周过程可知，滚动分为圆沿直线滚动（如图6）和圆绕点旋转（如图7）两种情况.

如图6，⊙O在△ABC边上滚动的情况，可如例1求解.

如图7，圆绕点（此点在圆周上）旋转，旋转一周，自转一圈，即圆的自转圈数（θ为圆旋转过的角度）.

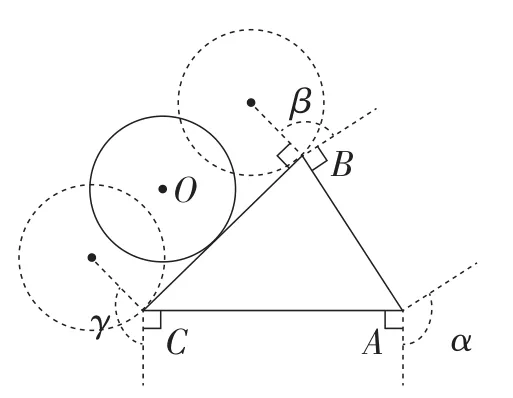
图6

图7

此题中⊙O分别绕点A，B，C旋转角α，β，γ，由三角形性质可知，α+β+γ=360°.∘

解：如图6，⊙O在△ABC边上滚动过的距离为AB+BC+CA=5+6+7=18 cm.这个过程中，⊙O自转圈数.

如图7，⊙O分别绕点A，B，C旋转角为α，β，γ，由三角形性质可知，α+β+γ=360°.这个过程中，⊙O自转圈数.

所以，当在△ABC外滚动一周时，⊙O自转了圈.

三、圆在圆周（曲线）上滚动

例3两个一元硬币，其中一个不动，另一个绕其做不滑动的滚动一周，问旋转的硬币自转几圈？

分析：正确理解“圆自转一周，是参照元素重回原位置”，对求解此题至关重要.一些学生会误解为：如图8，在⊙O2绕⊙O1的圆周滚动的过程中，参照点A到达点B的位置时（的长等于⊙O2的周长），⊙O2自转了一圈.这种误解也许来自“圆在直线上滚动”的问题图示的影响.事实上，圆在圆周上滚动时，既有滚动距离也有旋转，兼具例1与例2的特性.

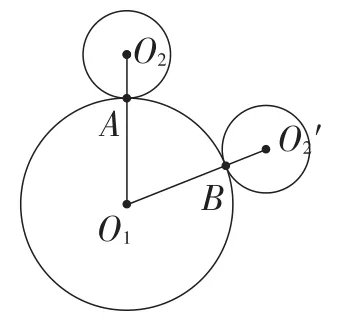
图8

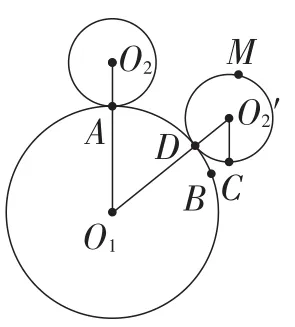
图9

本文开篇就特别强调了“圆自转一圈，是参照元素重回原位置”的重要性，也可以用更直观的说法“半径平行且方向相同”来理解.如图9，当⊙O2的半径O2A随着圆的滚动，旋转到O2C的位置时（O2A∥O2′C），⊙O2自转了1圈.可以看到，此时点C并未到达圆周与连心线的交点，对比两图会发现，图8中的⊙O2′已经自转一圈还多些.

问题：若⊙O2绕⊙O1的圆周滚动一周，⊙O2自转几圈？

如图9， ⊙O2自转了1圈时，O2A∥O2′C，设 ∠O1=∠O2=n，⊙O1的半径为R，⊙O2的半径为r.

由滚动可知，⊙O1的的长等于⊙O2的的长，得.

⊙O1的的长为为⊙O2自转1圈时滚动过的⊙O1的弧长.）

此时，如图10，点O2经过的路线长=2πr，（点为O2经过的路线长为 ⊙O1的周长，滚动圆的圆心经过一个自身周长的距离，为自转1圈.）