基于刀具姿态控制的指令点插补算法*

耿 聪, 吴玉厚，韩 旭

(1.沈阳建筑大学 a.高档石材数控加工装备与技术国家地方联合工程实验室；b.机械工程学院，沈阳 110168； 2.沈阳高精数控智能技术股份有限公司，沈阳 110168)

0 引言

五轴数控机床能够通过刀尖点位置坐标和刀轴矢量的变化达到灵活控制刀具位姿的目的，从而提高加工速度、精度和表面光洁度，在航空、汽车、模具制造等行业得到广泛应用[1-2]。指令点插补对加工精度和效率有着直接影响，是五轴数控加工中的关键问题[3]。

线性插补是五轴数控系统常用的指令点插补算法，该算法通过对机床各轴首末点位置坐标进行线性分割，实现刀具位姿变化[4]。在实际加工中发现，线性插补方式会导致下述问题产生。首先，五轴数控加工工件几何造型复杂，采用直线段对复杂曲线离散化，不仅会增加数据传输负担，而且在离散化过程中会产生不必要的误差。其次，由于刀轴矢量各分量与旋转轴位置坐标间存在非线性映射，采用线性插补法进行五轴数控加工时，无法控制刀具姿态[5]。最后，线性插补方法无法保证机床各轴速度和加速度的连续性，影响加工表面光滑度。

针对上述问题，本文提出一种基于刀具姿态控制的五轴数控加工指令点插补算法。在本算法中，刀尖点位置曲线可表示为参数样条曲线、Bezier曲线、B样条曲线或NURBS曲线等多种形式[6-9]，便于数据传输。在相关文献[10-11]中，对平面、圆锥面刀具姿态控制方法进行了研究，本文将采用样条曲线建立经过给定离散刀轴矢量的二阶连续刀具姿态曲线，以满足自由曲面加工中刀具姿态变化灵活多样以及旋转轴速度、加速度连续变化的需要。

1 算法的基本思想

采用本文所述算法进行插补时，可将五轴数控系统工作流程分为代码预处理、刀具姿态曲线拟合、刀尖点曲线拟合和实时插补四部分，算法代码预处理部分是后续刀具姿态曲线和刀尖点曲线拟合的基础，该部分将读取五轴数控程序确定刀具运动信息。数控加工程序可表示为如下格式[11]：

G05.0X_Y_Z_U_V_W_F_;

其中，刀尖点在X、Y、Z方向的坐标分量分别由X_、Y_、Z_后的数值确定，刀轴矢量在X、Y、Z方向的坐标分量分别由U_、V_、W_后的数值确定，F为该段程序对应的刀具进给速度。本算法的代码预处理部分将读取采用刀轴矢量编程方式形成的数控加工程序，确定刀尖点和刀轴矢量坐标。整体流程如图1所示。

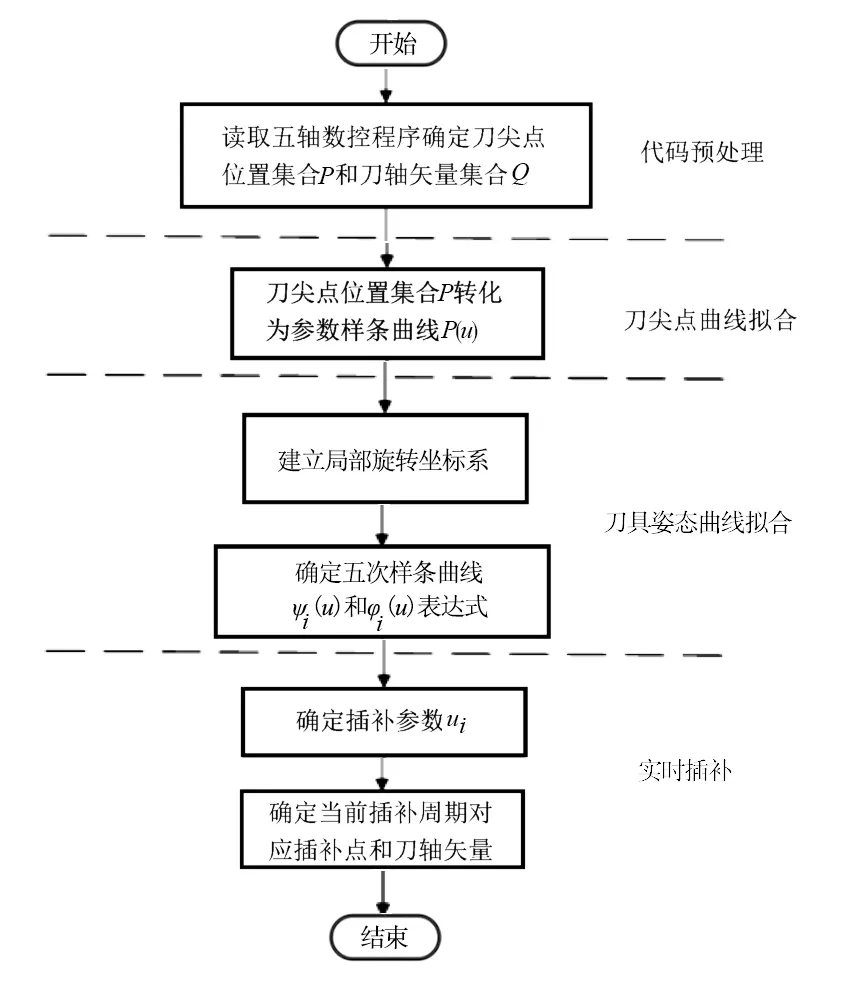
图1 本算法流程图

代码预处理部分根据给定的数控加工程序得到刀尖点位置集合P={Pk|Pk=(Pxk,Pyk,Pzk)且Pxk,Pyk,Pzk∈R,k=0,…,n}和刀轴矢量集合Q={Qk|Qk=(Qxk,Qyk,Qzk),|Qk|=1,k=0,…,n}后，直接对离散刀尖点Pk和刀轴矢量Qk进行加工，会带来机床各轴频繁加减速问题，影响加工效率和加工表面质量[12]。为避免这一问题的产生，刀尖点曲线拟合和刀具姿态曲线拟合部分将分别对离散刀尖点和刀轴矢量进行拟合，得到刀尖点曲线P(u)和刀具姿态曲线Q(u)。

刀尖点曲线拟合部分将离散刀尖点位置集合P={Pk|Pk=(Pxk,Pyk,Pzk)且Pxk,Pyk,Pzk∈R,k=0,…,n}转化为参数样条曲线P(u)：

P(u)=(x(u),y(u),z(u))u0≤u≤un

(1)

其中，u为曲线参数。P(u)可表示为参数样条曲线、Bezier曲线、B样条曲线或NURBS曲线等多种形式。

在实际加工中发现，五轴数控机床旋转轴速度和加速度的连续性对加工表面光洁度和加工效率等有着十分重要的影响。针对具体机床结构进行运动学分析可知，刀具姿态曲线各分量的二阶连续是实现机床旋转轴速度和加速度连续变化的前提条件[13]。因此，刀具姿态曲线拟合部分的主要功能是将代码预处理部分得到的离散刀轴矢量拟合为二阶连续的刀具姿态曲线。该部分首先根据首末刀轴矢量Q0和Qn建立局部旋转坐标系，用与ψk和φk相关的函数表示离散刀轴矢量Qk；而后，采用三次样条曲线近似估计ψk和φk的一、二阶导数值；最后，采用五次样条曲线进行拟合，得到经过刀轴矢量集合Q中各个离散刀轴矢量的二阶连续刀具姿态曲线。刀具姿态曲线拟合部分是实现五轴数控加工指令点插补的关键，该部分的具体实现步骤将在下一节进行详细说明。

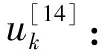
(2)

将第k个插补周期插补点对应参数值uk带入刀尖点拟合曲线P(u)和刀轴矢量拟合曲线Q(u)，即可得到下一插补周期的插补点P(uk)和对应刀轴矢量Q(uk)。

2 刀具姿态曲线拟合

刀具姿态曲线拟合是本算法的核心。该部分通过建立局部旋转坐标系，将单位矢量拟合转化为角度标量拟合，通过三次-五次样条曲线拟合得到二阶连续的刀具姿态曲线，进而保证机床旋转轴速度和加速度的连续性，下文将对其具体实现步骤进行详细说明。

2.1 刀具姿态控制模型

在代码预处理部分，通过读取数控程序，可确定待插补曲线起始点P0和终点Pn对应的刀轴矢量Q0和Qn。由刀轴矢量集合的定义可知，Q0和Qn均为单位向量。根据式(3)和式(4)，可建立局部旋转坐标系Q0-N-V：

(3)

(4)

则对于任意点Pk∈P，其对应刀轴矢量Qk可表示为：

(5)

其中，ψk是刀轴矢量Qk与刀轴矢量Q0和单位向量N所形成平面N-Q0的夹角，φk是刀轴矢量Qk在平面N-Q0上的投影与起始向量Q0间夹角，两角度可通过下式计算：

ψk=arcsin(Qk·V)

(6)

(7)

2.2 刀具姿态曲线的确定

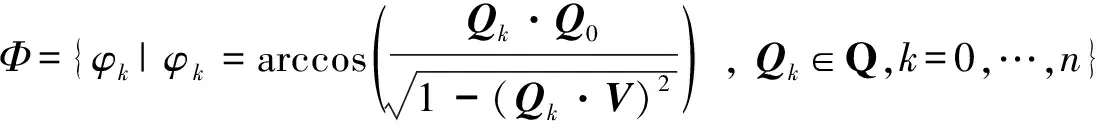
在进行曲线拟合前，首先需要确定ψk和φk对应的参数值uk，本文采用向心参数化方法确定对应参数：

(8)

其中，|Pk-1Pk|表示刀具沿Pk-1运动到Pk时的距离:

(9)

当确定ψk和φk对应的参数值uk后，将构造经过ψk和φk的三次样条曲线，确定参数值uk对应点处一、二阶导数。在此基础上，采用五次样条曲线构造满足二阶连续的曲线ψ(u)和φ(u)。下文将以{ψ0,ψ1,…,ψn}的拟合过程为例进行说明，{φ0,φ1,…,φn}的拟合过程类似。

假定由点ψi-2,ψi-1,ψi,ψi+1和ψi+2确定的三次样条拟合曲线ψi(u)如下式所示：

(10)

其中，b3i,b2i,b1i和b0i是ψi(u)曲线的系数。令Ii表示点ψi-2,ψi-1,ψi,ψi+1和ψi+2与拟合曲线ψi(u)上参数ui-2,ui-1,ui,ui+1和ui+2对应点间距离的平方和:

(11)

则Ii为以bki为变量的函数，为使函数Ii达到最小值，Ii对各变量bki的偏导数应满足：

(12)

上式可表示为:

(13)

将参数ui-2,ui-1,ui,ui+1,ui+2以及ψi-2,ψi-1,ψi,ψi+1,ψi+2代入式(13)，即可确定bki(k=0,1,2,3)的值，进而得到参数ui处对应值的一、二阶导数：

(14)

参数u0和u1处对应值的一、二阶导数分别等于ψ2(u0)和ψ2(u1)处一、二阶导数值，参数un和un-1处对应值的一、二阶导数分别等于ψn-2(un)和ψn-2(un-1)处一、二阶导数值。当确定参数uk对应点ψk的一、二阶导矢量后，刀轴矢量由Qk变化至Qk+1过程中，刀轴矢量与平面N-Qn间夹角ψk(u)的表达式如下所示：

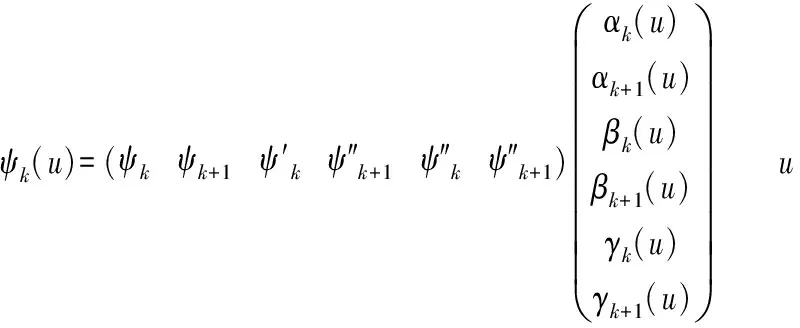
其中，αk(u),αk+1(u),βk(u),βk+1(u),γk(u)以及γk+1(u) 是五次样条曲线ψk(u)的系数：

3 实验

为验证本文所提出算法的有效性，将对图2所示S型试件进行加工仿真。为便于进行分析，下文将选择S型试件上的一条刀具轨迹进行说明，如图3所示。

图2 S型试件

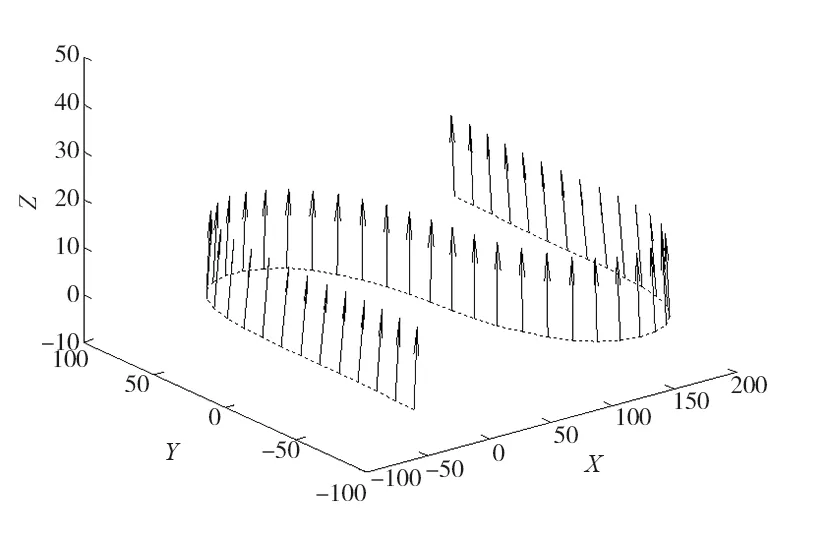
图3 刀具轨迹

图4所示为采用本文所述算法得到的刀具姿态曲线。由该图可知，所得到的刀具姿态曲线位于单位球面上且经过给定的离散刀轴矢量集合，说明本算法能够保证刀具姿态曲线上任意向量均为单位矢量。图中星号标记点为给定的离散刀轴矢量，说明所生成的刀具姿态曲线能够经过给定的离散刀轴矢量。

图4 刀具姿态曲线

图5所示为刀具姿态曲线各分量及其一、二阶导数图。该图进一步说明采用本算法得到的刀具姿态曲线经过给定的离散刀轴矢量，且曲线在x,y和z方向各分量均满足一阶和二阶连续的条件。图6说明采用本算法得到的刀具姿态曲线进行插补时，能够保证旋转轴速度和加速度连续变化。

图5 刀具姿态曲线各分量及一、二阶导数变化

图6 机床旋转轴速度和加速度曲线

4 结论

本文采用三次-五次样条曲线对离散刀轴矢量拟合得到二阶连续的刀具姿态曲线，能够保证加工中刀具经过数控加工程序确定的离散刀轴矢量序列以实现对刀具姿态的控制，丰富了五轴数控系统插补功能。基于刀具姿态控制的指令点插补算法避免了数据传输负担大、刀具姿态无法控制以及旋转轴速度、加速度不连续等问题，为提高复杂曲面整体加工效果奠定了良好基础。