IRB4400喷涂机器人运动学分析研究*
2019-01-03王征兵孙文磊
王征兵,孙文磊
(新疆大学 机械工程学院,乌鲁木齐 830046)
0 引言
随着汽车工业的不断发展,喷涂机器人已经成为汽车制造环节中不可或缺的核心自动化装备之一[1]。喷涂机器人的运动学分析是其动力学、运动控制和轨迹规划的研究基础,它包含了正运动学分析和逆运动学分析[2]。近年来,很多学者对机器人运动学都进行了研究,但研究对象相对老旧小众。文献[2]以IRB2400机器人为研究对象,采用传统的矩阵逆运算方法进行运动学求解。文献[3]对码垛机器人应用BP神经网络进行运动学求解。文献[4]应用动态模糊神经网络对KR16-2型机器人进行运动学求解。文献[5]对BP神经网络在机械手轨迹规划中的应用方法做了可行性分析。但这些未能将运动学智能求解算法应用到广泛使用的新型喷涂机器人当中。IRB4400喷涂机器人是ABB公司的一种机身紧凑型机器人,在车间喷涂过程中可有效节省空间,而以往文献中缺乏对该型喷涂机器人的运动学研究。因此对其进行运动学分析和仿真在科学研究和实际应用中具有十分重要的意义。
1 机器人D-H模型建立
ABB公司的IRB4400型喷涂机器人是具有6个自由度的关节型机器人,它由底座、髋关节、肩关节、肘关节、腕关节和喷枪组成,每个旋转关节都是一个自由度。其本体结构和旋转关节如图1所示。
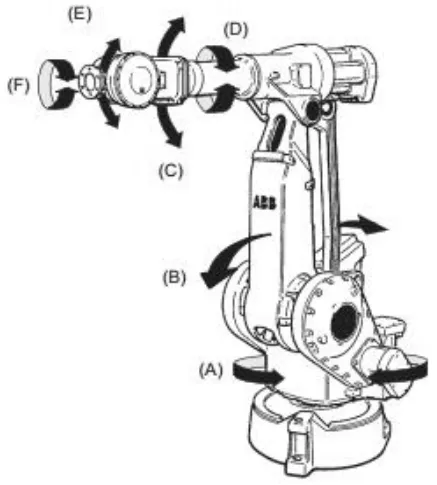
图1 IRB4400喷涂机器人本体结构
在对机器人进行运动学分析之前,首先要根据机器人的结构参数建立其数学模型。采用D-H法对该型喷涂机器人进行数学建模。建系主要原则为Xi和Zi-1垂直且相交,Yi根据右手规则确定[1]。建立的简化模型和D-H坐标系如图2所示。

图2 机器人简化模型和D-H坐标系
根据IRB4400机器人的连杆参数和图2所建坐标系可得其D-H参数如表1所示。表中连杆参数具体表示含义为:关节转角θi(°),关节距离di(mm),连杆长度ai(mm),连杆扭角αi(°)。

表1 IRB4400机器人D-H参数
2 正运动学分析

(1)
nx=S6(C4S1+S4(C1S2S3-C1C2C3))+
C6(C5(S1S4-C4(C1S2S3)-C1C2C3))-
S5(C1C2S3+C1C3S2)
(2)
ny=-S6(C1C4-S4(S1S2S3-C2C3S1))-
C6(C5(C1S4+C4(S1S2S3-C2C3S1))+
S5(C2S1S3+C3S1S2))
(3)
nz=S23S4S6-C6(C23S5+S23C4C5)
(4)
ox=C6(C4S1+S4(C1S2S3-C1C2C3))-
S6(C5(S1S4-C4(C1S2S3-C1C2C3))-
S5(C1C2S3+C1C3S2))
(5)
oy=S6(C5(C1S4+C4(S1S2S3-C2C3S1))+
S5(C2S1S3+C3S1S2))-
C6(C1C4-S4(S1S2S3-C2C3S1))
(6)
oz=S6(C23S5+S23C4C5)+S23C6S4
(7)
ax=-S5(S1S4-C4(C1S2S3-C1C2C3))-
C5(C1C2S3+C1C3S2)
(8)
ay=S5(C1S4+C4(S1S2S3-C2C3S1))-
C5(C2S1S3+C3S1S2)
(9)
az=S23C4S5-C23C5
(10)
px=200C1+890C1C2-150C1S2S3-140S1S4S5-
140S23C1C5+150C1C2C3-880C1C2S3-
880C1C3S2-140C1C2C3C4S5+140C1C4S2S3S5
(11)
py=200S1+890C2S1-880C2S1S3-880C3S1S2+
140C1S4S5-150S1S2S3-140S23C5S1+150C2C3S1-
140C2C3C4S1S5+140C4S1S2S3S5
(12)
pz=70S23S45-150S23-890S2-70S4-5S23-
880C23-140C23C5+680
(13)
在Robotics Toolbox中根据表1中D-H参数建立IRB4400喷涂机器人仿真连杆模型[6],并输入给定的6个初始关节角度分别为0,pi/2,0,0,pi,0,得到其初始状态的仿真连杆模型如图3所示。

图3 IRB4400机器人仿真图
可见图3中的仿真连杆模型和图2中所建的D-H坐标简化模型相同,并在输入初始各关节角后得到了机器人末端位置和姿态,验证了机器人正运动学分析和建模的正确性。
3 逆运动学分析
机器人逆运动学分析问题的实质就是由笛卡尔空间向关节空间的非线性映射问题。传统的求解方法主要有封闭解法和数值解法,这些方法虽然可以进行机器人逆运动学求解,但在实际求解过程中运算复杂,且可能存在多个解,不便于应用[7]。而BP神经网络具有逼近任何复杂的非线性系统的能力,所以应用BP神经网络智能算法进行机器人逆运动学的分析求解具有很大的优势。
3.1 BP神经网络算法逆运动学求解
BP神经网络是一种按照误差逆向传播算法训练的多层前馈网络,它能学习和存贮输入输出数据的映射关系,但不需要表示出这种关系的数学方程。它的学习算法是使用最速下降法,通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小[3]。其结构一般有三层,即为:输入层,隐含层和输出层。
在Matlab的神经网络工具箱中,对IRB4400机器人逆运动学的求解问题进行BP网络的建立,训练及预测仿真的算法流程如图4所示。

图4 BP神经网络算法流程图
BP网络输入端为机器人末端位姿矩阵表达式(2)~式(13),输出端为机器人的6个关节角数据。但在构建BP网络时输入端数据太多,会使网络过于复杂不便于实际应用,所以可将末端位姿矩阵式(2)~式(10)按照ZYZ欧拉角变换得到α,β,γ这3个参数形式,其具体变换式如下[6]:
α=Atan2(ay,ax)
β=Atan2(axcosα+aysinα,az)
γ=Atan2(-nxsinα+nycosα,
oycosα-oxsinα)
(14)
隐含层节点的主要功能是选取并保存训练样本的内在规律,过少的节点会使网络不能全面概括样本规律;过多的节点则会降低网络泛化能力,造成训练时间的延长。在实际应用中,隐含层节点的个数可以通过下面的经验公式(15)来计算[5]:
(15)
式中,n为输入层节点数,l为输出层节点数,分别取为6,α=1~10。代入得到m的范围为5~13。根据试验确定最佳隐含层为1层,节点个数为7,最终得到BP神经网络结构如图5所示。

图5 逆运动学求解BP神经网络结构图
输入层节点的传递函数选择对数S型传递函数logsig,输出层节点的传递函数选择线性传递函数purelin。由于LMBP算法是一种既有高斯-牛顿法的局部收敛性,又具有梯度下降法的全局特性的数值优化快速算法,它比梯度法快得多。所以,训练函数选择LMBP算法训练函数trainlm。网络学习函数选择动量梯度下降权值和阈值学习函数learngdm[8]。构建好的BP网络Matlab代码如下:
net=newff(inputn,outputn,7,{′logsig′,′purelin′},′trainlm′,′learngdm′)
对机器人各关节变量θi在其关节角范围内分别取不同值,组合得到5000组关节角(θ1,θ2,θ3,θ4,θ5,θ6)。然后在MATLAB Robotics Toolbox 中由机器人正运动学解表达式(11)~式(13)和欧拉角变换式(14)得到5000组输入数据(α,β,γ,px,py,pz)。为了避免不同量纲的样本数据对网络训练效果产生较大的影响,需要对样本原始数据按照下式进行归一化处理。
(Xi-Xmin)/(Xmax-Xmin)
(16)
最后随机选择4900组数据作为神经网络的训练样本,100组数据作为网络的测试样本,设置网络迭代次数为100,学习速率为0.001,学习精度为0.0001。至此,BP网络逆运动学求解的前期工作准备完毕。
3.2 仿真结果及分析
根据所建的BP神经网络和数据样本在Matlab中进行编程仿真分析,结果见图6。
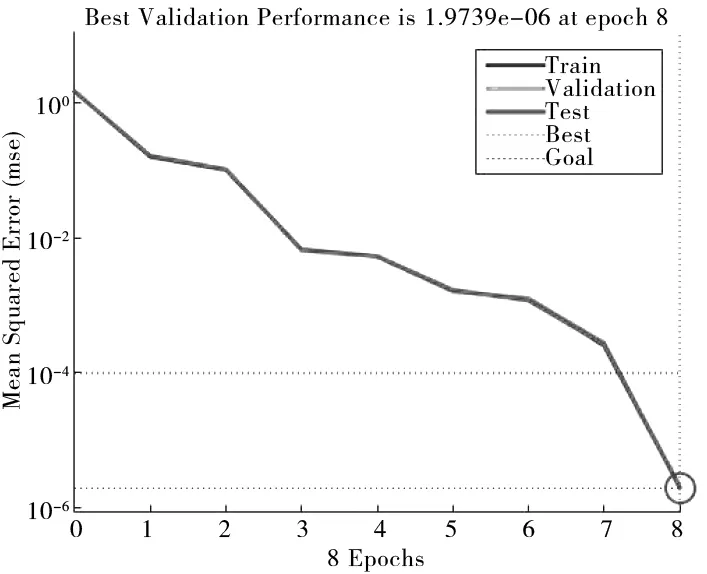
图6 BP网络训练过程均方差下降曲线
图6所示为LMBP算法训练函数trainlm的训练过程曲线。分析图中结果可知,样本训练和测试过程的均方差在迭代8次后可达1.9739×10-6,能够快速达到预设精度。
根据测试样本由BP神经网络可以得出100组6个关节角的预测输出,为了更清楚直观地表示预测输出关节角和期望输出关节角的契合程度,这里只取出关节角3的预测输出数据和测试样本数据进行对比分析,如图7所示。由图可直观地观察到预测关节角和期望关节角基本重合。
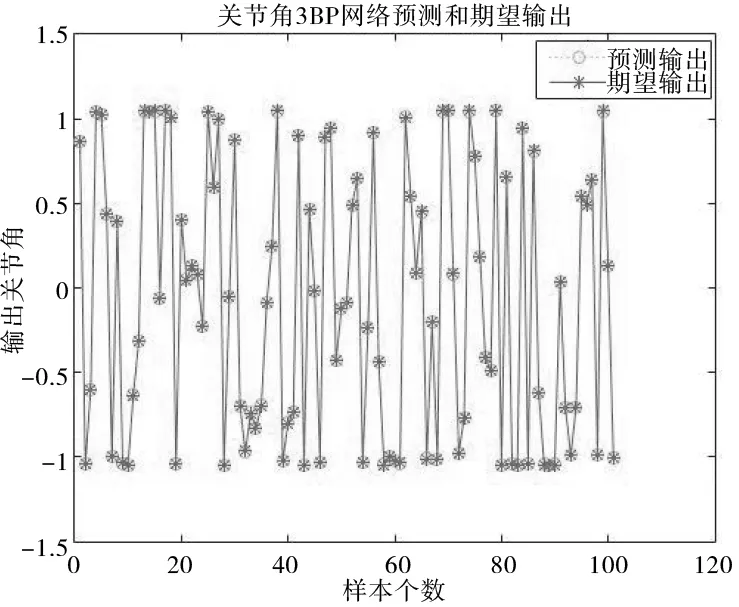
图7 关节角3的预测输出和期望输出
为了更加清楚地表示关节角3的预测输出与期望输出关节角之间的契合程度,需要进行误差分析,一般来说,相对误差更能反映出网络预测的可信程度。通过观察,相对误差如图8所示最高不超过3%,根据工程经验,一般相对误差不超过5%即可视为有效数据。

图8 关节角3 的BP网络预测相对误差
通过上述仿真结果及仿真数据分析可知,BP神经网络用于IRB4400喷涂机器人逆运动学求解,仿真结果能够达到喷涂作业的要求,其仿真分析具有参考意义。
4 机器人运动学验证
4.1 工作空间仿真
机器人的工作空间是机器人末端能够到达的所有空间位置点的集合。工作空间的大小代表了机器人的活动范围,其在运动学分析及轨迹规划中有重要意义。为了对喷涂机器人正运动学的分析结果进行直观的验证,采用蒙特卡洛法对IRB4400喷涂机器人的工作空间进行仿真[9]。采用蒙特卡洛法分析机器人工作空间的具体方法如下:
(1)利用机器人正运动学方程,在Matlab中求出机器人末端位置坐标的方程;
(2)在IRB4400机器人各关节角规定范围内依照下式:
(17)
(3)将各随机关节变量代入机器人末端位置坐标方程中即可得到机器人工作空间。
通过Matlab编程仿真,得到三维工作空间和XOY平面工作空间投影如图9所示。

图9 机器人工作空间和XOY平面投影仿真图
可以直接观察到IRB4400喷涂机器人的工作空间,直观地验证了机器人正运动学分析的正确性,并为后面的运动轨迹规划做好了准备。
4.2 运动轨迹仿真
在IRB4400机器人的工作空间内选取机器人末端的两个位姿矩阵T1和T2,将矩阵元素进行ZYZ欧拉角变换,得到含有6个位姿元素(α,β,γ,px,py,pz)的两组矩阵分别为:
T1(-2.9437,-0.5421,0.0501,-0.5649,-0.1084,2.2895)
T2(-2.8831,0.2136,0.0316,286.7460, -33.9028,162.1481)
取100个时间步长{0:0.05:5}(单位s)作为插值节点,用标量插补函数tpoly在两组位姿矩阵元素之间进行5次多项式平滑插值处理[6],得到100组位姿元素插值点。然后将这些位姿元素插值点按前述方法进行归一化处理,将其作为训练好的BP神经网络的输入端元素,进行网络预测求解,得到机器人分别处于这100组位姿时的各关节角度。
再用解得的各关节角在Matlab的机器人工具箱中对IRB4400机器人进行驱动仿真,初始和终止速度设置为零[10],然后用plot绘图命令就可以得到机器人末端轨迹图和运动仿真过程的各关节角度,角速度和角加速度曲线图如图10所示。
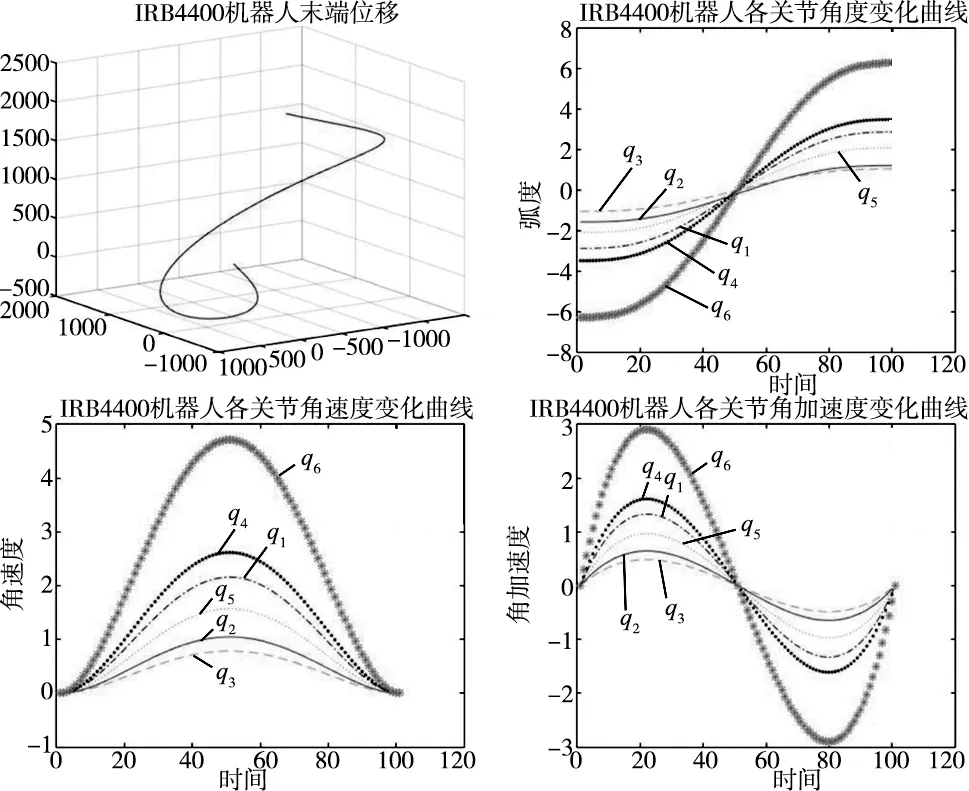
图10 机器人运动轨迹仿真图
观察运动仿真图,BP神经网络预测求解得到的各关节角度,角速度和角加速度曲线平滑而连续,没有关节突变现象产生,满足机器人运行稳定,冲击振动小的原则,验证了BP神经网络对IRB4400喷涂机器人进行逆运动学求解的有效性,避免了大量的矩阵逆运算和繁琐的计算公式,提高了运动学求解效率,便于实时控制。
5 结论
对IRB4400喷涂机器人进行了结构参数分析,建立了其D-H数学模型,在Robotics Toolbox中,编写Matlab程序进行了正运动学分析,得到了初始状态下的仿真连杆模型,与所建的D-H简化模型相同;针对一般机器人逆运动学求解方法复杂低效的问题,研究了BP神经网络算法在该型机器人逆运动学求解中的应用,得到了网络预测输出关节角和期望输出关节角对比图,分析结果,其预测精度可满足喷涂作业要求;并基于蒙特卡洛法编程实现了该型机器人的工作空间仿真,直观地验证了正运动学分析结果的正确性;最后通过运动轨迹仿真,得到了机器人末端运动轨迹、各关节角、角速度和角加速度平滑连续的曲线,满足机器人运行稳定,冲击振动小的原则,验证了逆运动学算法的有效性。以上分析结果提高了该新型喷涂机器人的运动学求解效率,对IRB4400喷涂机器人实际编程作业效率的提高具有参考性价值。
