巧解直线与圆的综合问题

■陈国林

直线与圆是解析几何初步的内容，是学习圆锥曲线的基础，但是很多同学在初学时常因知识掌握得不够牢固，而导致解题时出错。下面以例题形式呈现，给出几个有关直线与圆的问题的巧解方法，希望能给同学们带来启示。

一、理清基本概念

例1下列命题中正确的有( )。

①直线的斜率为tanα，则直线的倾斜角是α;

②直线的倾斜角为α，则直线的斜率为tanα;

③由于垂直于x轴的直线的斜率不存在，所以垂直于x轴的直线的倾斜角也不存在。

A.0个 B.1个

C.2个 D.3个

解：直线的斜率为tanα，只有当α∈[0，π)时，α才是直线的倾斜角，①错误;任一直线的倾斜角均为α∈[0，π)，而当时，直线的斜率不存在，②错误;当直线垂直于x轴时，倾斜角为，③错误。应选A。

评注:对于直线与倾斜角问题，需要明确倾斜角α∈[0，π)，所有直线都有唯一的倾斜角，但当倾斜角为90°时，直线的斜率不存在。

二、重视直线斜率不存在的情况

例2直线l过点P(-1，2)且到点A(2，3)和点B(-4，5)的距离相等，则直线l的方程为

解法1：当直线l的斜率存在时，设直线l的方程为y-2=k(x+1)，即kx-y+k+2=0。由题意可得即，解得，此时直线l的方程为)，即x+3y-5=0。当直线l的斜率不存在时，直线l的方程为x=-1，也符合题意。综上可得，直线l的方程为x+3y-5=0或x=-1。

解法2：当AB∥l时，可得k=kAB=则直线l的方程为y-2=，即x+3y-5=0。当l过AB的中点时，由AB的中点为(-1，4)，可得直线l的方程为x=-1。综上可知，直线l的方程为x+3y-5=0或x=-1。评注:部分同学在求解直线的方程时，常常因忽略直线的斜率不存在的情况，而导致漏解或错解。实际上，在求解此类问题时，若能够借助图形，采用数形结合的思想，会使得题目更直观，且大大降低解题的出错率。

三、巧用截距为零

例3过点P(2，3)并且在两坐标轴上的截距相等的直线方程为( )。A.2x-3y=0

B.3x-2y=0或x+y-5=0

C.x+y-5=0

D.2x-3y=0或x+y-5=0

解：当所求直线与两坐标轴的截距均不为0时，设该直线的方程为x+y=a，把点P(2，3)代入所设的方程，得a=5，则所求直线的方程为x+y=5，即x+y-5=0。当所求直线与两坐标轴的截距均为0时，设该直线的方程为y=kx，把点P(2，3)代入所设的方程，得，则所求直线的方程为y=，即3x-2y=0。综上可得，所求直线的方程为x+y-5=0或3x-2y=0。

评注:解答本题时，首先，需要分所求直线与两坐标轴的截距均为0和均不为0两种情况进行讨论;其次，通过把已知点的坐标代入求出直线方程。

四、分清倾斜角的取值范围

例4经过点P(0，-1)作直线l，若直线l与连接点A(1，-2)，B(2，1)的线段总有公共点，则直线l的倾斜角α的取值范围是。

解：如图1所示，为使直线l与线段AB总有公共点，则需kPA≤k≤kPB，而kPB＞0，kPA＜0。当k＜0时，α为钝角;当k=0时，α=0;当k＞0时，α为锐角。因为kPA=所以-1≤k≤1。当0≤k≤1时，当-1≤k＜0时故倾斜角α的取值范围为

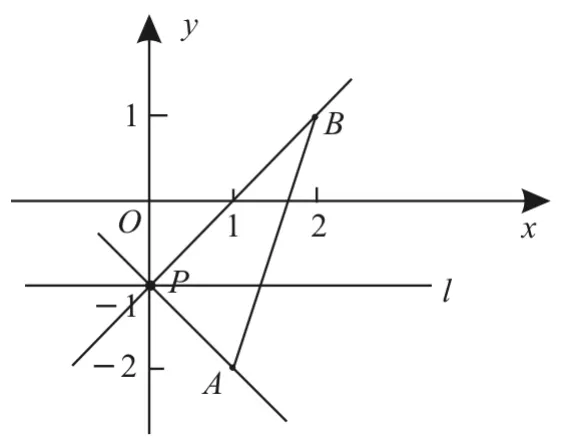
图1

评注:在求倾斜角α的取值范围时，如果忽略了倾斜角α∈[0，π)，则会误解为α∈。在解答这类题目时，如果能够借助数形结合思想，将会使问题变得简单直观。

五、注意特殊情况

例5已知线段PQ两端点的坐标分别为点P(-1，1)和点Q(2，2)，若直线l∶x+my+m=0与线段PQ有交点，则实数m的取值范围是

解：如图2所示，直线l∶x+my+m=0过定点A(0，-1)。当m≠0时，kPA=-2，因为，所以或，解得或当m=0时，直线l的方程为x=0，与线段PQ也有交点。综上可得，实数m的取值范围为

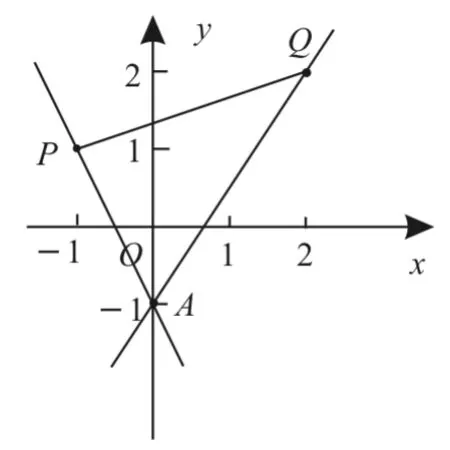
图2

评注:本题中m=0是个特殊情况，若忽视，会导致所求的实数m的取值范围为

六、清楚直线和圆的位置关系

例6已知直线l∶mx+y-2m-1=0，圆C∶x2+y2-2x-4y=0，当直线l被圆C所截得的弦长最短时，实数

解：由题意知，直线l过定点(2，1)，设点A为(2，1)，而圆C∶(x-1)2+(y-2)2=5，其圆心C为(1，2)。当直线l被圆C所截得的弦长最短时，直线AC⊥l，则-1，解得m=-1。

评注:过圆内的一点作直线，该直线与圆一定相交，且所截得的最长的弦为过该点的直径，最短的弦为过该点与直径垂直的弦。

七、牢记圆的半径r＞0

例7过点(1，2)总可作两条直线与圆x2+y2+kx+2y+k2-15=0相切，则实数k的取值范围是

评注:二元二次方程x2+y2+Dx+Ey+F=0表示圆时，需要满足D2+E2-4F＞0，如果忽略了这一条件，会造成待定参数k的取值范围扩大。

八、挖掘隐含条件

例8若动点(x，y)在圆(x-2)2+y2=4上，求6x2+8y2的最大值。

解：由(x-2)2+y2=4得y2=4x-x2，所以6x2+8y2=6x2+8(4x-x2)=-2x2+32x=-2(x2-16x+64-64)=-2(x-8)2+128。因为0≤x≤4，所以当x=4时，6x2+8y2的最大值为96。

评注:圆(x-2)2+y2=4是一个封闭的图形，表示以(2，0)为圆心，以2为半径的圆，所以x的取值范围不是R，而是[0，4]。解答本题时，若挖掘不出这一隐含条件，会误认为当x=8时，6x2+8y2的最大值为128。

九、全面考虑情况

例9圆C∶(x-5)2+(y-1)2=36上到直线4x+3y+2=0的距离为1的点的个数为

解：因为圆C的半径为6，圆心(5，1)到直线4x+3y+2=0的距离为5＜6，又因为r-d=6-5=1，所以圆C∶(x-5)2+(y-1)2=36上到直线4x+3y+2=0的距离为1的点的个数为3。

评注:圆上的点到一条直线的距离等于定值，这样的点可能有0个，1个，2个，3个，4个等情况，解答此类问题时，需要谨慎思考，要注意区分直线与圆的交点个数与圆上的点到一条直线的距离等于定值的点的个数的区别。