一道圆的最值问题的变式探索

■胡 磊 齐展修 华 伟

题目已知直线l的方程为x+y-6=0，M为圆x2+y2-4x+3=0上的任一点，设点M到直线l的距离为d，则d的最大值为

分析：求出已知圆的圆心与半径，利用圆心到直线的距离求解。

解：圆x2+y2-4x+3=0化为(x-2)2+y2=1，可知圆心坐标为(2，0)，半径为1。

直线l的方程为x+y-6=0，M为圆x2+y2-4x+3=0上的任一点，设点M到直线l的距离为d。

名师评析:本题考查直线与圆的位置关系的综合应用，考查计算能力。圆上的点到直线距离的最值问题，一般转化为圆心到直线的距离问题来解决。本题的解题过程体现了最值问题中的以静制动的思想方法。

变式1：已知点A，B(1，0)，点P为圆C∶x2+y2+2x=0上的任一点，则△PAB面积的最大值为

分析：求出已知圆的圆心与半径，由于线段AB为定长，于是所求问题可转化为求点到直线的距离的最大值。

解：由x2+y2+2x=0，可得(x+1)2+y2=1，可知圆心C(-1，0)，半径r=1。

名师评析:对于这类问题，可以转化为圆心到直线的距离的最大值求解。

变式2：直线x+y+2=0分别与x轴，y轴交于A，B两点，点P在圆(x-2)2+y2=2上，则△ABP面积的取值范围是

分析：本题与变式1的命题方向如出一辙。由于AB是定长，所以所求问题可转化为圆心到直线的最值问题来求解。

解：由x+y+2=0，令x=0，得y=-2，令y=0，得x=-2，所以点A(-2，0)，

因为点P在圆(x-2)2+y2=2上，所以点P到直线x+y+2=0的距离的最值就是圆心到直线AB的距离的最值。

设AB边上的高为h，圆心(2，0)到直线x+y+2=0的距离是则。

名师评析:本题也是转化为圆心到直线距离的最值问题求解的，圆上的点到直线的最大距离等于d+r，最小距离等于d-r。

变式3：点P(x，y)是直线kx+y+3=0上一动点，PA，PB是圆C∶x2+y2-4y=0的两条切线，A，B是切点，若四边形PACB面积的最小值为2，则k的值为

分析：本题也可转化为圆心到直线的距离的最小值问题求解。

解：根据题意画出图形，如图1所示。

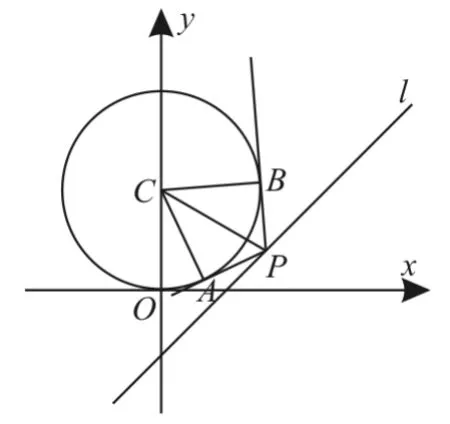
图1

故当|PC|最小时，面积取得最小值。

因为|PC|的最小值即为点C到直线kx+y+3=0的距离d，而，所以。

名师评析:本题仍然是转化为圆心到直线的最小值求解的。