例谈直线与圆的最值问题

■蓝云波

解析几何中的直线与圆是高考的核心考点，其中，涉及直线与圆的最值问题，考查频率颇高，命题灵活，蕴含的数学思想方法非常丰富。因此，这部分内容一直以来都是同学们学习的一大难点。为帮助同学们提高学习效率，解决这一学习难点，下面以直线与圆关系的典型例题为例，来谈谈这类问题的解决方法。

例1 分别过点A(1，3)和点B(2，4)的直线l1和l2互相平行，且有最大距离，则l1的方程是

(图略)当直线l1与l2分别与线段AB垂直时，直线l1与l2之间有最大距离，且，此时kAB=，所以k=-1。故l的方程为yl113=-(x-1)，即x+y-4=0。

发现两条直线的临界位置是解答本题的关键，发现后再利用斜率公式和直线的点斜式方程实现问题的求解。

例2 在平面直角坐标系xOy中，直线l1∶kx-y+2=0与直线l2∶x+ky-2=0相交于点P，当实数k变化时，点P到直线xy-4=0的距离也随之变化，则距离变化的最大值为

由题意得直线l1的斜率为k，且过点A(0，2)，直线l2过点B(2，0)，且直线l1⊥l2，所以点P落在以AB为直径的圆C上，其中，圆心坐标为C(1，1)，半径为r=。则圆心到直线x-y-4=0的距离为，所以点P到直线x-y-4=0的最大距离为d+r=

发现两条直线过定点且两条直线互相垂直的关系是解答本题的关键，在此基础上利用圆的性质实现问题的求解。

例3已知两点A(0，-3)，B(4，0)，若点P是圆x2+y2-2y=0上的动点，则△ABP面积的最小值为

如图1，过圆心C向直线AB作垂线交圆于点P，连接BP，AP，这时△ABP的面积最小。

图1

面积问题的求解是解析几何中的一大热点。通过分析本题我们发现三角形中的AB边为定值，故只需求出此边上的高的最小值，再利用数形结合思想，不难实现问题的解决。

例4已知圆C1∶(x-2)2+(y-3)2=1，圆C2∶(x-3)2+(y-4)2=9，M，N 分别是圆C1，C2上的动点，P为x轴上的动点，则的最小值为

画出简图，如图2。

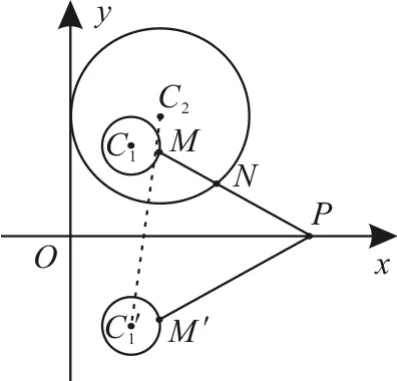
图2

☉C1关于x轴对称的☉C1'的圆心C1'为(2，-3)，半径仍为1，☉C2的圆心为(3，4)，半径为3。设点M'为点M关于x轴的对称点，由图2可知，，且当C2，M'，P，N，C'1在同一条直线上时取得最小值，记为又因为所以的最小值为52-4。

此题是解析几何中的经典题型，解答时通过数形结合，把多动点问题化归为定点问题，具有较强的灵活性。

例5已知P是直线kx+4y-10=0(k＞0)上的动点，过点P作圆C∶x2+y2-2x+4y+4=0的两条切线，A，B是切点，C是圆心，若四边形PACB的面积的最小值为2，则k的值为

由题意可得圆C的标准方程为(x-1)2+(y+2)2=1，则圆心C为(1，-2)，半径为1。由题意知直线与圆相离，如图3所示，S四边形PACB=S△PAC+S△PBC，而又因为，所以取最小值时，S△PAC=S△PBC取得最小值，此时，CP垂直于直线kx+4y-10=0。因为四边形PACB面积的最小值为，所以，所 以。又因为k＞0，所以k=3。

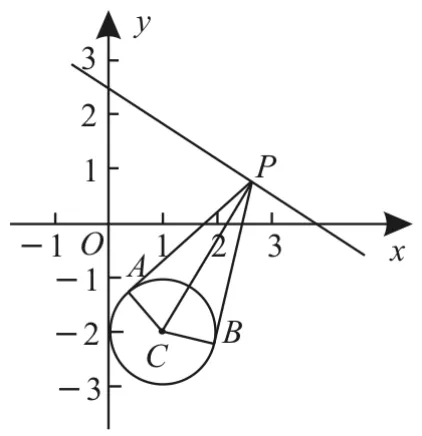
图3

本题是与切线相关的直线与圆的综合问题，解题的关键是通过分析将问题转化为直线上的点与圆心的最值问题。

例6在平面直角坐标系xOy中，点A为(0，3)，直线l∶y=2x-4，设圆C的半径为1，圆心在直线l上。若圆C上存在点M使得则圆心C的横坐标a的最大值与最小值之和为

因为圆心在直线l上，所以可将圆心C设为(a，2a-4)，则圆C的方程为(x-a)2+(y-2a+4)2=1。设点M为(x，y)，因为所以，化简得x2+y2+2y-3=0，即x2+(y+1)2=4，所以点M在以点D(0，-1)为圆心，2为半径的圆上。因为点M(x，y)在圆C上，所以圆C与圆D有公共点，则，即由≥1，得5a2-12a+8≥0，解得a∈R。由，得5a2-12a≤0，解得所以圆心C的横坐标a的最大值与最小值之和为

本题以阿波罗尼斯圆为背景，考查了圆与圆的位置关系，这一命题特点凸显了近年来高考数学命题的热点——以数学文化为背景考查考生的数学素养，这一点应引起大家足够的重视。

例7已知点P(x，y)在圆C∶x2+y2-6x-6y+14=0上。

(2)求x+y的最大值与最小值。

(3)求x2+y2的最大值与最小值。

(1)方程C∶x2+y2-6x-6y+14=0可变形为(x-3)2+表示圆上的点P与原点连线的斜率，显然当PO(O为原点)与圆相切时，斜率最大或最小，如图4所示。

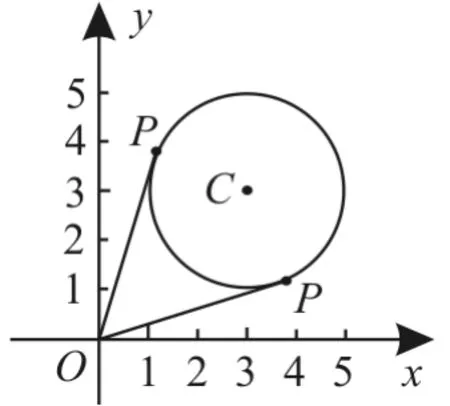
图4

设切线方程为y=kx，即kx-y=0，由圆心C(3，3)到切线的距离等于圆的半径，可得，解得所以的最大值为最小值为

(2)设x+y=b，则b表示动直线y=-x+b在y轴上的截距，显然当动直线y=-x+b与圆(x-3)2+(y-3)2=4相切时，b取得最大值或最小值，如图5所示。

图5

由圆心C(3，3)到切线x+y=b的距离等于圆的半径，可得，即，解得所以x+y的最大值为6+22，最小值为6-22。

(3)x2+y2可表示为，其几何意义为圆C上一点与原点O的距离d的平方，显然(r为圆C的半径)。因为，所以，所以(32-2)2≤，即所以x2+y2的最大值为最小值为

本题是一道直线与圆的综合问题，三个问题所求的表达式均具有较强的几何意义，分别以斜率、截距、距离的平方为背景进行命题的构建，是一道兼具知识与能力的好题。

例8已知圆M的圆心M在x轴上，半径为1，直线l∶被圆M所截得的弦长为3，且圆心M在直线l的下方。

(1)求圆M的方程。

(2)设点A 为(0，t)，点B为(0，t+6)，其中-5≤t≤-2，若圆M是△ABC的内切圆，求△ABC面积S的最大值和最小值。

(1)设圆心 M 为(a，0)，由已知得圆心M到直线l的距离，所以又因为圆心M在直线l的下方，所以8a-3＞0，所以8a-3=5，解得a=1。故圆M的方程为(x-1)2+y2=1。

(2)设直线AC的斜率为k1，直线BC的斜率为k2，则直线AC的方程为y=k1x+t，直线BC的方程为y=k2x+t+6。由方程组得点C的横坐标为xC=因为所以S=因为圆M与直线AC相切，所以，解得同理可得所以k-k=12，所以因为-5≤t≤-2，所以-2≤t+3≤1，所以-8≤t2+6t+1≤-4，所以Smax=

本题具有较大的运算量，解题中利用了轮换思想，这种思想在解析几何中具有较强的通性通法。通过面积表达式的求解，将问题转化为求函数最值问题，这是解析几何的命题热点。