一种柔直换流器子模块电容容值优化方法

刘 勇，王 森

（海军驻上海江南造船（集团）有限公司军事代表室，上海 201913）

0 引言

柔直换流器（Modular multilevel converter，MMC）在柔性直流输电（VSC-HVDC）领域中得到了广泛的应用。MMC由多个子模块（submodules，SMs）组成。子模块电容的成本大约是整个子模块成本的三分之一，子模块电容的重量和尺寸超过整个模块的一半。因此，减小电容的容值可降低成本、提高变换器的功率密度，具有重要的现实意义。

到目前为止，已经提出了一些减小电容的方法。文献[1]和[2]提出了注入高频环流和高频共模电压的方法，该方法仅适用于电机驱动等中低压应用场合。文献[3]对子模块电容的电压波动进行了分析，通过注入二次谐波环流减小了电容电压的低频波动。通过注入离线计算的二次和四次环流[5]，可减小电容电压的波动，但该方法对电路参数较为敏感。文献[6]提出了一种实时计算环流的方法。

本文首先简要分析了 MMC的工作原理，然后建立了子模块电容电压波动的数学模型，找出了影响电容电压波动的因素。为了使子模块电容容值最小化，仅考虑电容电压波动的幅值大小，而不考虑电容电压波动的谐波次数，提出一种优化方法。通过选取合适的二次环流注入比，对子模块电容电压波动的幅值进行了优化。与抑制环流的方法相比，该方法可以显著降低子模块电容的电压波动，从而减小子模块电容的容值需求。使用文献[7]中的模型计算该方法的功率损耗，与常规方法相比，该方法的损耗几乎不变。最后，仿真结果验证了所提方法的有效性。

1 MMC的工作原理

三相MMC的拓扑结构如图1所示，它由3个相单元组成。其中，每个相单元由上、下2个桥臂组成。每个桥臂又由N个子模块和桥臂电感串联构成。桥臂电感为 MMC提供限制和控制臂电流的能力。子模块的拓扑结构是一个半桥电路（half-bridge，HB），它由两个开关管（S1，S2）和一个缓冲电容（C）组成。电容平均电压UC与直流母线电压Ud的关系为

由于三相对称，下面以 a相为例进行分析。仅考虑交流侧在功率因数为 1的正常工作模式，并且忽略桥臂电感的压降，a相的等效电路模型如图2所示。

桥臂电流可分为直流电流、交流相电流和环流 3个分量。上臂电流ipa和下臂电流ina可以表示为

式中：Id为直流母线电流。a相的电流ia的表达式为

iacir、ibcir、iccir分别是 a、b、c三相的环流。这三个环流的约束关系为

桥臂电压由直流电压、交流相电压和共模电压组成。上桥臂电压vpa和下桥臂电压vna可以表示为

式中：Ud为直流母线电压。a相电压ua得表达式为

ucom是三相的共模电压，它的大小取决于调制策略。如果采用正弦波调制，则不需要注入共模电压，因此

如果使用三次谐波注入调制，那么需要注入幅值为基波幅值六分之一的三次谐波，此时ucom为

定义调制比M为

当采用正弦波调制时，M的取值范围为 0～1。当采用三次谐波注入调制时，M的取值范围为0～1.15。

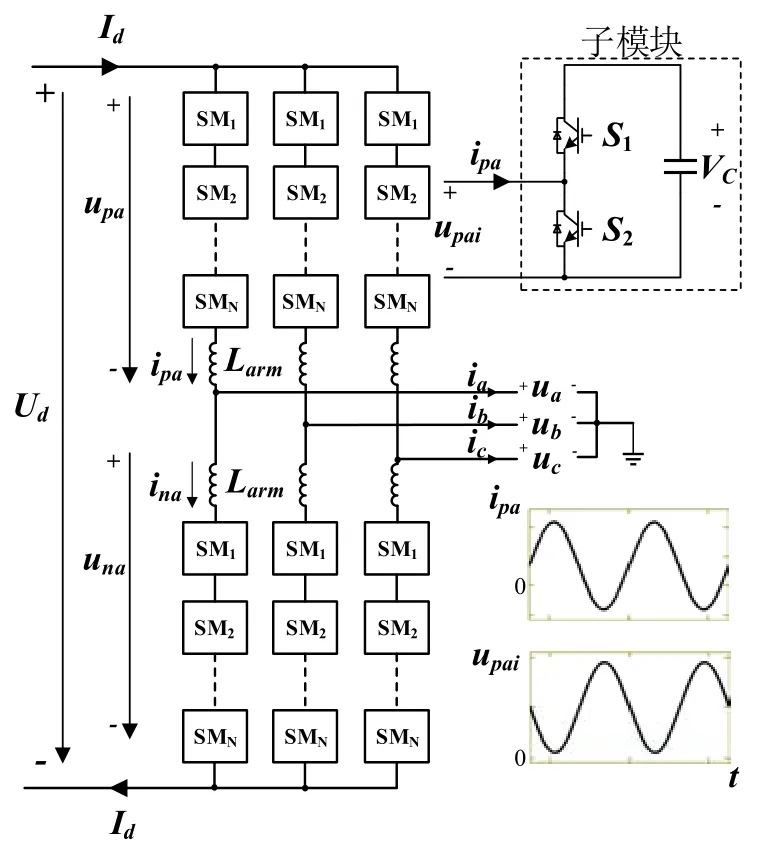
图1 MMC的电路拓扑

图2 a相等效电路模型

2 电容电压波动的数学模型

当 MMC工作在稳态时，子模块电容电压一个周期内在平均值附近波动，且平均电压一直保持不变。每个子模块可以看作是一个二端口网络。如果忽略二端口网络内部的能量损耗，那么输入到子模块的能量全部被电容C吸收。一个电容的能量变化为

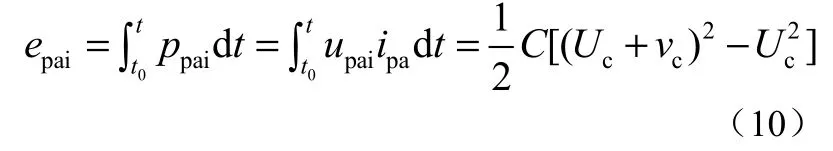
式中：Uc为子模块电容平均电压；vc是子模块电容电压的交流分量；t0为电容电压，等于Uc的初始时刻；t为初始时刻t0之后的任意时刻。由于波动幅值远小于电容电压平均值，交流分量vc的平方项可以忽略，可以得到交流分量的表达式为

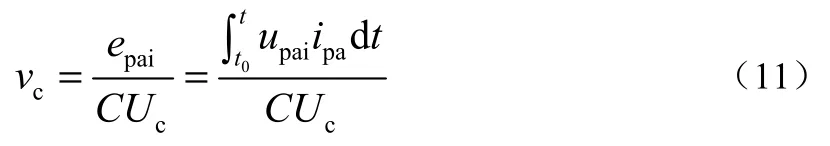
假设所有子模块的电容电压都均衡良好，由于桥臂电感两端的电压相比直流电压和交流电压都非常小，可以忽略，因此整个上桥臂电容的能量变化为

由上式可推得电容电压波动（交流分量）的表达式为

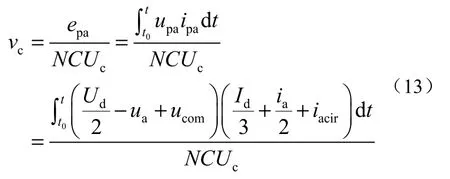
如果忽略变换器的能量损耗，交流相电流与直流母线电流的关系为

当采用正弦波调制时，电容电压波动的解析表达式为

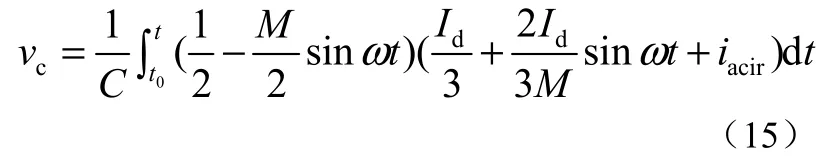
当采用三次谐波注入调制时，电容电压波动的解析表达式为

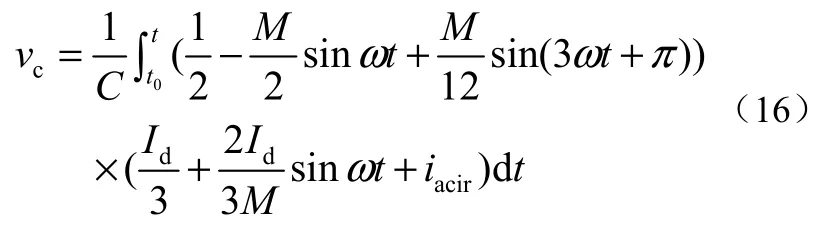
3 电容最小化优化方法

基于电容电压波动的数学模型，对于给定的调制比和选定的调制方法，通过注入适当大小的环流可以使子模块电容电压纹波最小化。

设注入二次环流的表达式为

定义注入比x为二次环流幅值与直流母线电流的比值，为

此时，当采用正弦波调制时，电容电压波动的表达式为

当采用三次谐波注入调制时，电容电压波动的表达式为

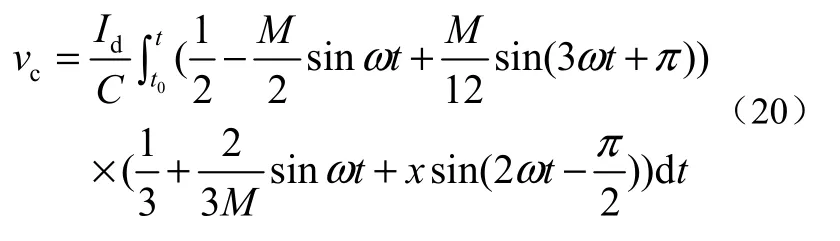
为了在相同电容容值下获得最小的电压纹波，应选择适当的注入比来使vc的峰值（vcpp）最小化。电容电压纹波（vcpp）与二次环流幅值（I2）之间的关系可根据式（19）或（20）得出。显然，电容电压纹波与直流母线电流成正比。同时，电容电压纹波与交流侧频率和子模块电容容值成反比。因此，应更加关注调制比、注入比与电容电压纹波之间的关系。在特定的应用场合中，调制比通常是固定的。对于选定的调制方法和给定的一组交流频率、调制比、直流母线电流和子模块电容容值，电容电压纹波仅与注入比有关。

3.1 注入环流的选取

选择几个典型的调制比进行子模块电容容值优化：0.9、0.95、1和1.05。

当M＜1时，可以使用正弦波调制或三次谐波注入调制。图3给出了当M=0.9和M=0.95时，电容电压纹波与注入比之间的关系。

当M=0.9时，正弦波调制比三次谐波注入调制更具有优势，因为前者的电容电压纹波最小值更小。在这种情况下，应该使用正弦波调制。当x＞0.7时，电容电压纹波几乎不变。但注入比过大会导致效率降低。因此，可以选择注入比为0.7。注入比等于0表示环流受到抑制的常规方法。与常规方法相比，电容电压纹波降低到原来的54.8%。

当M=0.95时，同样应该使用正弦波调制。当注入比等于0.671时，电容电压纹波取得最小值。因此，注入比应取0.671。与常规方法相比，电容电压纹波降低到原来的47%。

图3 电容电压纹波与注入比的关系，M＜1

当M≥1时，只能采用三次谐波注入调制。图4给出了当M=1和M=1.05时，电容电压纹波与注入比之间的关系。

M=1时，当注入比等于 0.620时，电容电压纹波达到最小值。因此，在这种情况下，注入比应取0.620。与常规方法相比，电容电压纹波降低到原来的49.6%。

M=1.05时，当注入比等于0.518时，电容电压纹波达到最小值。此时，注入比应取0.518。与常规方法相比，电容电压纹波降低到原来的41.6%。

vcppmax与调制比之间的关系如图5所示。注入比的选取见表1。可以得到以下结论：调制比越大，注入比可以越小。这意味着注入的环流可以较小，注入的电流对变换器效率和开关管电流应力影响较小。

图4 电容电压纹波与注入比的关系，M≥1

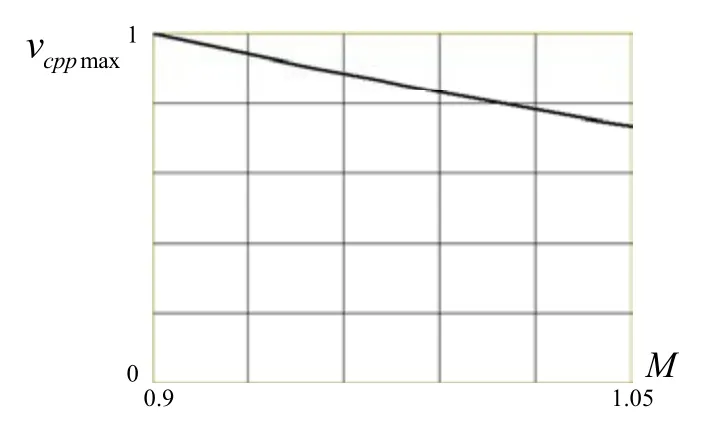
图5 vcppmax与调制比的关系

表1 注入比的选取

3.2 开关管电流应力比较

注入环流将导致开关管电流应力的增加。在图 6中，ipamax为IGBT的电流应力，Id为直流母线电流。在常规方法中，开关管的电流应力近似等于直流母线电流。与常规方法相比，所提方法在M=0.9时开关管电流应力增加65%，M=1.05时开关管电流应力增加54%。

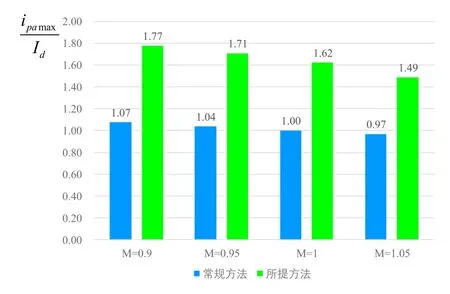
图6 开关管电流应力对比

当M=1.05时，注入环流对开关管电流应力的影响最小。综合考虑容值减小比例、变换器效率和开关管电流应力，应选取调制比为 1.05，以达到电路最佳工作状态。

3.3 控制方案

系统的控制方案如图 9所示。调制波是输出电流控制环路输出、环流控制环路输出和直流分量的叠加。

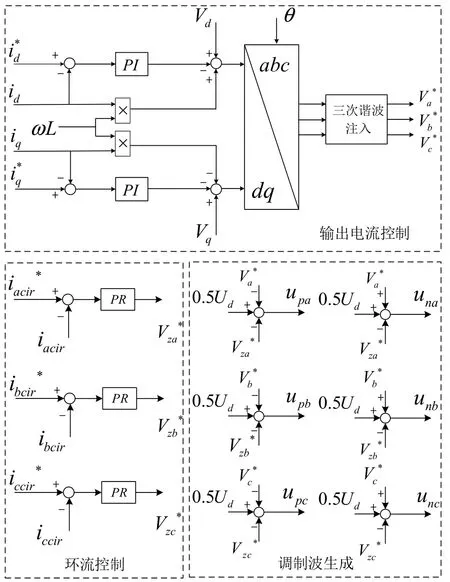
图9 控制方案

4 仿真结果

为了验证所提方法，在 MATLAB/SIMULINK中建立了基于 MMC系统的并网逆变器模型。直流侧为直流电压源，交流侧为三相电压源，采用定输出电流控制策略。并网MMC模型的仿真参数见表2。常规方法和所提方法的仿真结果分别如图10和图11所示。

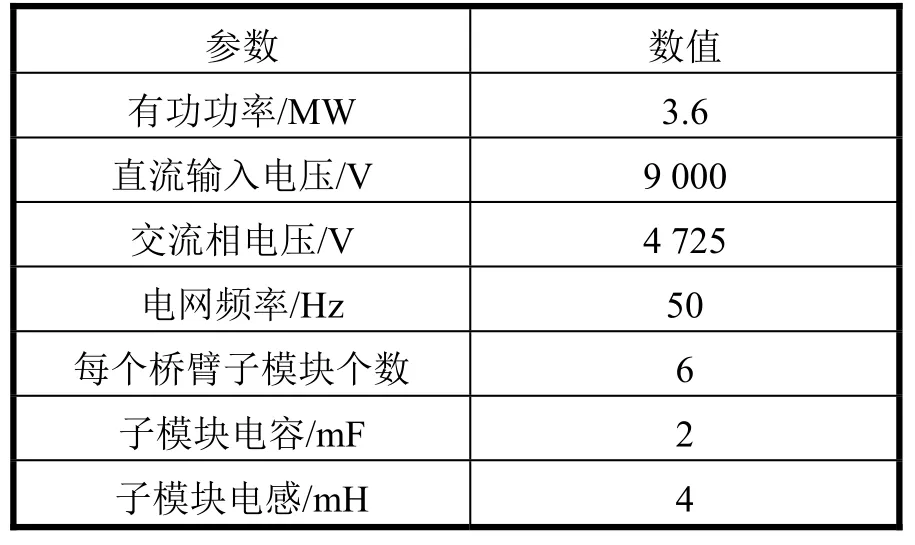
表2 并网MMC模型的仿真参数

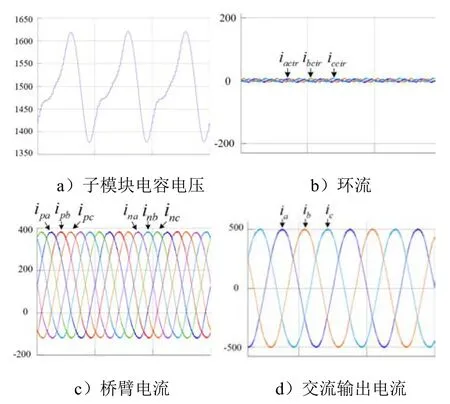
图10 常规方法的仿真结果

图 10a）中常规方法的电容电压纹波为250 V，图11a）中所提的优化方法的电容电压纹波为100 V，这表明所提方法的电容容值需求减少到常规方法的 40%。图 10b）中环流的幅值为 0。在图 11b)中，环流的幅值为0.518ID。图10c）中常规方法的电流应力为380 A。图11c）中所提方法的电流应力为600 A，约为常规方法的158%。在图10d）和图11d）中，输出交流电流的波形相同。仿真结果验证了理论分析的正确性。

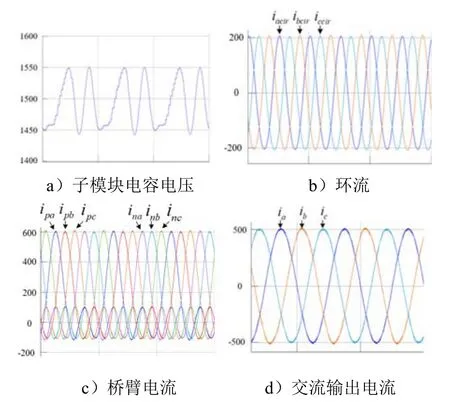
图11 所提方法的仿真结果

5 结论

为了使 MMC子模块电容最小化，本文提出了一种优化方法。在调制比固定时，通过选择合适的调制方法、注入特定大小的二次环流，对子模块电容电压波动的峰峰值进行优化。与常规方法相比，所提方法可以将电容容值需求减少到 40%。该优化方法同样适用于任意调制比、其他调制方式以及更多频次的环流注入。