模糊等价关系下的犹豫模糊粗糙集及其应用

齐　爽，王艳平



模糊等价关系下的犹豫模糊粗糙集及其应用

*齐爽，王艳平

（辽宁工业大学理学院，辽宁，锦州 121001）

首先通过对长度不同的犹豫模糊元进行补齐来定义犹豫模糊集新的交并运算，在Pawlak近似空间中利用新的运算建立粗糙犹豫模糊集模型；然后将Pawlak近似空间推广到一般犹豫模糊近似空间，利用犹豫模糊元间的相似度获得犹豫模糊近似空间中对象间的模糊关系矩阵，再利用模糊集的传递闭包法将模糊相似矩阵转化成模糊等价矩阵，在此基础上建立犹豫模糊信息系统中的粗糙集模型，研究犹豫模糊信息系统的属性约简。最后通过一个算例来说明犹豫模糊信息系统的属性约简方法。

犹豫模糊集；粗糙犹豫模糊集；犹豫模糊粗糙集；属性约简

0 引言

自1965年，Zadeh提出模糊集理论[1]以来，模糊集得到了相当广泛的推广。例如，K.Atanassov提出了作为模糊集扩展形式的直觉模糊集[2]；之后Atanassov和Gargov在直觉模糊集的基础上提出区间直觉模糊集[3]的概念等。但是，当遇到模糊性较高的实际问题时，就很难在多个可能值中选出恰当的值作为隶属度（或非隶属度）。这时，模糊集、直觉模糊集以及区间值模糊集等概念就不能合理地进行表述。为了更加客观的表达人们在决策时的犹豫程度，Torra在2010年引入了犹豫模糊集[4]的概念，对于决策中的不确定性问题犹豫模糊集能更有效地进行刻画。

Zadeh提出了相似关系[5]的概念，模糊集的相似度被广泛应用在决策、聚类分析、机器学习、近似推理、模式识别等领域。Pappis和Karacapilidis在1995年将模糊集合相似性度量应用到模糊关系方程[6]中；2005年，袁修久、张文修对模糊粗糙集的包含度和相似度[7]进行研究；2015年，林娟、米据生等定义了两种相似度量方法，并讨论了这两种度量方法之间的关系[8]。Pawlak等人于1982年提出了粗糙集理论[9]，粗糙集理论是一种处理不完整和不确定性知识的重要数学工具，经典的粗糙集模型是基于等价关系对论域中的样本进行划分和聚类的，把属性相同的聚成一类。由于犹豫模糊信息系统中很难满足完全相同的属性值，因而经常采用的方法是用犹豫模糊值的相似度来对它们的等价程度进行刻画，为论域的划分提供度量的标准。但是利用模糊相似关系只能得到论域的覆盖，无法得到它的精确划分。文献[10]利用模糊关系的传递闭包对区间值模糊信息系统的建模进行了讨论，本文将此方法应用在犹豫模糊信息系统中，建立基于模糊等价关系的犹豫模糊粗糙集模型，讨论在给定相似水平下的分类约简与核的计算方法。

1 预备知识

首先回顾一下犹豫模糊集的一些基本概念。

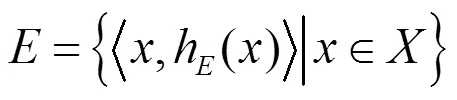
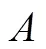
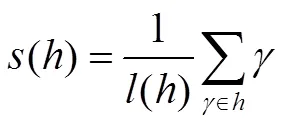
根据文献[11]可得犹豫模糊集的相似度公式为：

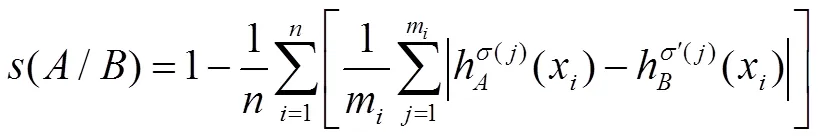
相似度是描述两个集合之间的贴近程度的，由于犹豫模糊元都表现为集合的形式，所以也可以研究两个犹豫模糊元之间的相似度。利用上面给出的犹豫模糊集的公式，可以得到下面的犹豫模糊元的相似度公式：

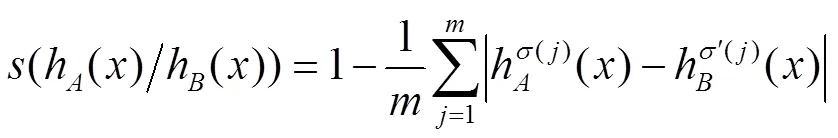
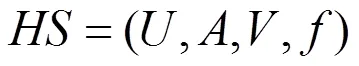
2 粗糙犹豫模糊集

正如文献[10]中指出的，Torra的交、并运算不满足吸收律。这不但与经典模糊集合的情况不符，也与交、并运算的实际目标相违背。在各种信息系统中，我们通常将给定的信息集合看成信息粒。那么在犹豫模糊信息系统中，若将每个犹豫模糊集看成是一个知识粒，我们希望通过交、并运算实现信息粒的细化与泛化，这样，Torra的交、并运算就无法满足。为此，本文给出新的犹豫模糊集的交、并运算。利用上节提出的新的延拓方法，即用犹豫模糊元中所有隶属度可能值的平均值补齐其长度，可以先将两个犹豫模糊元通过数值延拓使其含有元素个数相等，在此基础上再进行犹豫模糊元以及犹豫模糊集的运算。

本文利用前面给出的数值延拓方法，定义新的犹豫模糊包含关系如下。

由定义2.3可直接得到下面的结论。

定理2.1表明利用本文定义的犹豫模糊集的交、并运算和包含关系，就可以通过交、并运算实现信息粒的细化与泛化。下面利用新的交、并运算来建立粗糙犹豫模糊集模型。

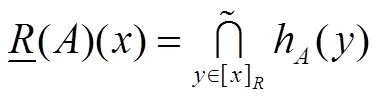
由定义2.4不难验证该粗糙犹豫模糊集有以下性质：

3 基于模糊等价关系的犹豫模糊粗糙集

由于Pawlak近似空间中的等价关系过于严格，犹豫模糊信息系统中的犹豫模糊值很难满足等价关系，因而需要进一步研究模型的推广形式。文献[10]可以得到犹豫模糊信息系统容差关系的相关定义及性质，首先利用上面给出的犹豫模糊元的相似度公式来定义犹豫模糊值信息系统上的容差关系。

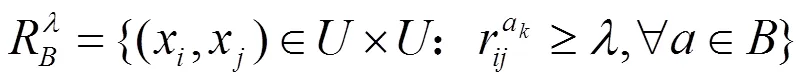
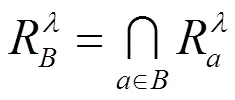
综上，表明性质3.1的容差关系弱于模糊等价关系。目前的研究一般用容差类替代等价类来划分度量论域。

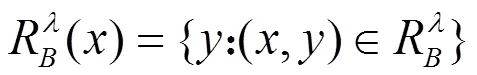
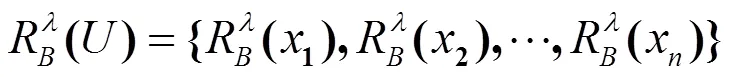
下面基于模糊等价关系建立犹豫模糊值信息系统的粗糙集模型。

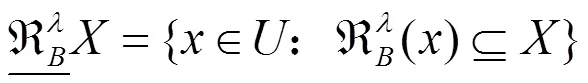
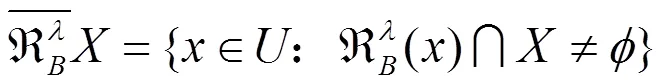
由定义3.3容易得到下面的性质。

4 模糊等价关系下的犹豫模糊值信息系统约简

本节将基于上节建立的犹豫模糊粗糙集模型，给出犹豫模糊信息系统的属性约简。参考文献[10]可以给出下列定义和性质。

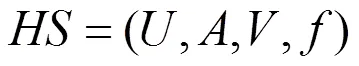
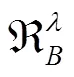
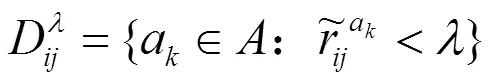
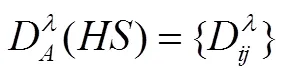
根据定义4.2可得到犹豫模糊值信息系统的属性约简判定定理。

定理4.2与定理4.3给出了模糊等价关系下犹豫模糊值信息系统的属性约简方法及其判定定理。

根据定义4.2，可定义犹豫模糊值信息系统上的分辨函数如下：

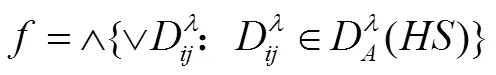
基于犹豫模糊值信息系统上的模糊等价关系，可得到下面的属性约简方法：

下面将通过一个算例来说明犹豫模糊信息系统的属性约简方法。

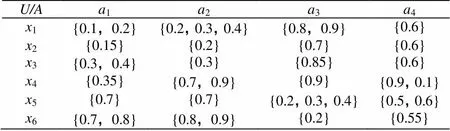
表1 犹豫模糊信息系统

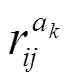
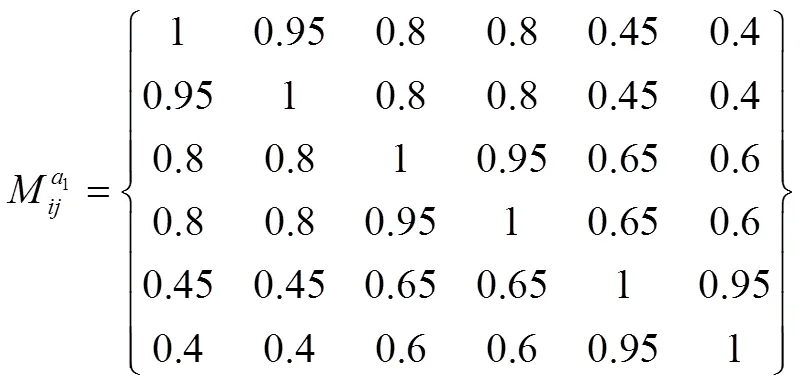
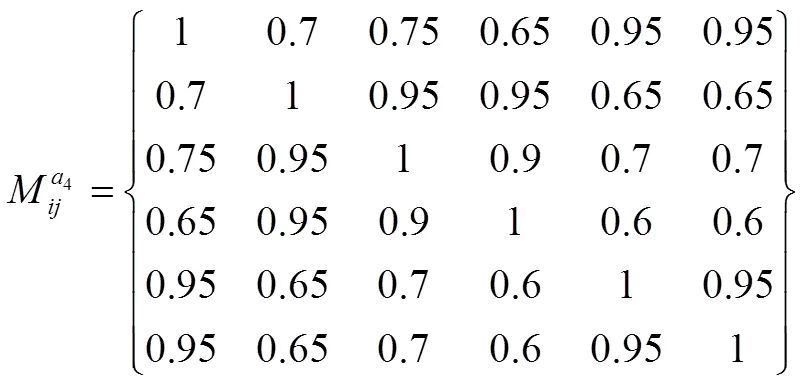
根据定义4.2可得分辨矩阵为：

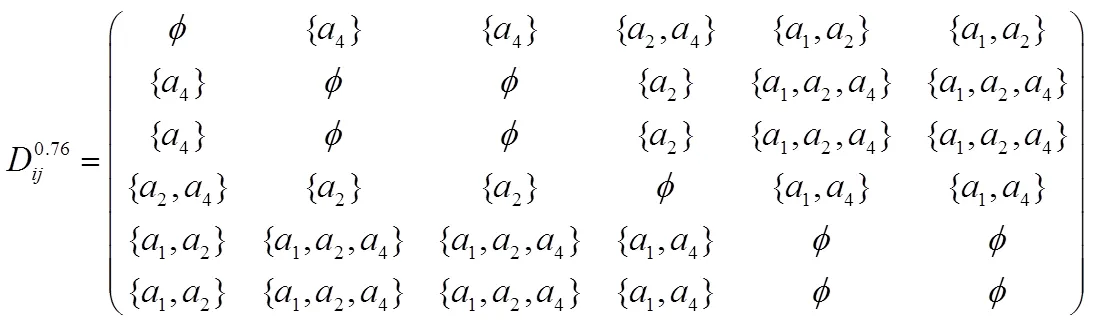
于是分辨函数为：

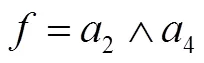
5 结束语

本文用均值对长度不等的犹豫模糊元进行补齐，然后定义犹豫模糊集新的交并运算，并基于经典的等价关系建立了粗糙犹豫模糊集模型。利用犹豫模糊元的相似度得到了犹豫模糊信息系统中对象间的容差关系，分析了现有的容差关系在犹豫模糊值聚类中的不足，构建了犹豫模糊值信息系统上的一种模糊等价关系，同时在模糊等价关系的基础上建立了犹豫模糊值信息系统的粗糙集模型。最后研究了在模糊等价关系下犹豫模糊值信息系统的属性约简，给出了有关的判定定理，并通过实际算例说明了属性约简方法的合理性和有效性。

[1] Zadeh L A. Fuzzy sets[J]. Information and Control, 1965, 8: 338-353.

[2] Atanassov K.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,1986,20(1):87-96.

[3] Atanassov K, Gargov G. Interval-valued Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,1989,31(3):343- 349.

[4] Torra V. Hesitant fuzzy sets[J]. International Journal of Intelligent Systems, 2010, 25: 529-539．

[5] Zadeh L, Similarity relations and fuzzy orderings[J]. Information Science, 1970,3:177-200.

[6] Pappis C, Karacapilidis N. A comparative assessment of measures of similarity of fuzzy values[J]. Fuzzy Sets and Systems,1993,56:171-174.

[7] 袁修久,张文修. 模糊粗糙集的包含度和相似度[J].模糊系统与数学,2005(1):111-115.

[8] 林娟,米据生,解滨. 粗糙集的两种相似性度量[J].计算机科学,2015,42(6):97-100.

[9] Pawlak Z.Rough sets[J].Internationl Journal of Computer and Information Sciences, 1982, 11(5): 341-356.

[10] 郭庆. 基于粗糙集理论的不确定信息系统及其决策研究[D].合肥:合肥工业大学,2017.

[11] Xu Z S, Xia M M. Distance and similarity measures for hesitant fuzzy sets[J].Information Sciences, 2011, 181: 2128-2138．

[12] 王国胤. Rough 集理论与知识获取[M].西安:西安交通大学出版社,2001.

[13] 高新波. 模糊聚类分析及其应用[M].西安：西安电子科技大学出版社,2004.

HESITANT FUZZY ROUGH SET BASED ON SIMILARITY AND ITS APPLICATION

*QI Shuang, WANG Yan-ping

(Science College, Liaoning University of Technology, Jinzhou, Liaoning 121001, China)

Firstly, the hesitant fuzzy sets with different lengths are complemented to define the new intersection operation of hesitant fuzzy sets. The new operation is used to establish the rough hesitant fuzzy set model in Pawlak approximation space. Furthermore, the Pawlak approximation space is extended to the general hesitant fuzzy approximation Space, using the similarity between hesitant fuzzy elements to obtain the fuzzy relation matrix between objects in hesitant fuzzy approximation space, and then transform the fuzzy similar matrix into fuzzy equivalent matrix by using the transitive closure method of fuzzy set, and establish a rough set model in hesitant fuzzy information system on this basis to study the attribute reduction of hesitant fuzzy information systems. And an example is given to illustrate the attribute reduction method of hesitant fuzzy information system.

hesitant fuzzy sets; rough hesitant fuzzy sets; hesitant fuzzy rough sets; attribute reduction

1674-8085(2018)05-0001-06

O159

A

10.3969/j.issn.1674-8085.2018.05.001

2018-06-11；

2018-08-19

*齐爽(1993-)，女，辽宁阜新人，硕士生，主要从事粗糙集理论研究及其应用(Email:1842215880@qq.com);

王艳平(1965-)，女，辽宁锦州人，教授，硕士，硕士生导师，主要从事粗糙集理论研究及其应用(Email:44879633@qq.com).