离散粒子群优化算法实现MapReduce负载平衡
2018-12-28李安颖
李安颖,陈 群,宋 荷
(西北工业大学计算机学院,陕西 西安 710072)
0 引言
Hadoop是由Apache开源组织开发的、具有高可靠性和高可扩展性的存储与分布式并行计算平台[1]。MapReduce是Hadoop的核心模型之一,广泛应用于大数据处理[2]。
MapReduce模型将计算分为Map和Reduce两个处理阶段。在Map阶段,由各Mapper对输入的数据元组进行分区处理,并将具有相同分区值的元组传送给同一个Reducer进行相关的计算。Hadoop系统默认采用的是Hash分区法,同时支持Range和用户自定义分区法。由于Map阶段产生的数据块大小不一,因此在Reduce阶段容易造成数据的Reduce节点分布不均衡,从而产生Reduce阶段的数据倾斜[3-5]。一旦发生数据倾斜,会使得各个节点的Reduce节点的负载不均衡,造成某些节点的Reduce任务相对于其他节点Reduce任务执行时间延长,进而延长了整个Reduce阶段的运行时间,从而影响整个任务的执行效率。
本文在充分研究了现有MapReduce数据平衡算法的基础上,提出一种基于离散粒子群算法的Reduce阶段数据负载平衡解决方法,以提高系统的稳定性。该方法将数据分区策略与智能分析算法相结合,构建将数据分区均衡的目标函数,并利用粒子群算法寻找数据分区的较优解,来解决数据分区的不平衡问题。
1 问题描述及模型构建
当前使用智能算法解决MapReduce调度的文献较多,但都没有深入地解决系统计算效率问题[6-8]。同时,对于解决Reduce阶段数据倾斜问题的研究工作也较少。避免数据倾斜的常用方法有两种:一是在Mapper运行程序中加入采样策略;二是先对输入数据进行预处理,再对数据进行制定分区策略[5]。前一种方法,当Mapper运行到特定时刻,根据采样所得到的分布信息,对发生数据量倾斜的分区进行一次拆分[4]。但该方法并没有给出一个通用的调整时机。后一种方法则增加了文件的处理时间。
在数据Map阶段完成后,待处理的数据块的数量为m,经Map处理得到各个数据块的数据量,分别为D1,D2,…,Dm。其中,Di表示第i块数据的数据量。假设当前系统的Reduce节点个数为M,且每个节点的处理能力相同。在采用Reduce进行处理前,需要计算如何在M个节点分配m个数据块,使得各个Reduce节点的负载尽量均衡,即实现各节点分配的数据量的差最小,并能达到数据平衡的目标。
假设m个数据块的Reduce分配向量为v={v1,…,vi,…,vm},1≤i≤m,i≤vi≤M。vi表示第i个数据块被分配到第vi个Reduce节点上。根据分配向量分配的各Reduce节点的数据量为R1,…,Rj,…,RM,1≤j≤M。Rj表示第j个Reduce节点分配的所有数据块的数据量之和。构建如下目标函数:
(1)
式中:R为数据量均值。
(2)
该方法求解的最终目标是寻找最佳的分配向量:v={v1,…,vi,…,vm},使得式(1)的值尽可能小。
2 粒子群算法求解目标函数
2.1 离散粒子群算法
粒子群算法是一种群体智能进化的算法,是多个粒子参照一定的规则指导进行的随机搜索[9-10]。基于生物学理论,单独的粒子代表一个物种,粒子群构成了一个种群。定义当前全局最优粒子代表当前种群中优势最强、生命力最强的物种,而个体历史最优代表该物种在其进化过程中所保留的最优的、最适应环境的生命形态。当前生命力最强的物种未必永远是生命力最强的,因此需要保存、学习其他各物种中最优的、最适应环境的生命形态,以保留该种群潜在的更优的生命因素。基于运动学理论,单独的粒子是空间中运动的单个质点粒子。粒子的运动既具有随机性,又具有导向性。离散粒子群算法将离散值作为待优化的变量,进而寻找最优解。
2.2 构建粒子
首先,对通过Map处理后输出的数据进行聚合,即获取各个Map的输出数据,并将其聚集在一个集合中。该集合的维数为n,整个集合数据的总和与各个Map输出的数据的和相同。然后,使用分配向量构建粒子,即构建粒子为n维向量x={x1,…,xi,…,xn}。其中,1≤xi≤M构成了一个分区方式,即一个解。在离散粒子群算法中,每个解构成了一个粒子。
考虑到粒子在运行优化的过程中,可能出现不满足1≤xi≤M条件的情况。因此,在粒子获取新的位置后可按照如式(2)进行调整,使其满足1≤xi≤M。
(3)
2.3 粒子群算法设计
2.3.1 粒子群算法步骤
设搜索空间的维度为n维,总粒子数为N。在每一次迭代中,所有的粒子在n维空间中进行“移动”以搜索全局得到最优解。粒子的速度和位置通过以下更新公式计算得到:
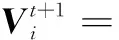
(4)
(5)
式中:i为群中的第i个粒子;t为迭代次数;ω为惯性因子;C1和C2为学习因子,均为正常数;Pi为第i个粒子迄今为止搜索到的最优位置,即局部最优解;Pg为整个粒子群迄今为止搜索到的最优位置,即全局最优解;Vi为第i个粒子的速度向量;Xi为粒子i的位置向量。
则在n维问题的空间中:
Vi={Vi1,Vi2,…,Vin}
(6)
Xi={Xi1,Xi2,…,Vin}
(7)
使用函数Rand()产生一个(0,1)之间的随机数。第d维(d1≤d≤N)的位置变化范围为[-XMAX,XMAX] ;速度变化范围为[-VMAX,VMAX] 。
粒子群的初始位置和速度通过随机函数进行随机产生,然后使用式(4)~式(5)进行迭代计算,直至找到较优解。
2.3.2 惯性因子及粒子速度
ω值越大,粒子的全局搜索能力越强,适用于对求解空间进行大范围探察;ω值越小,粒子的局部搜索能力越强。选择一个合适大小的ω,可以平衡全局和局部搜索能力,并可通过较少的迭代次数得到最优解。
为了平衡局部搜索能力以及全局搜索能力,设置惯性因子ω。ω的具体参数值根据试验数据的大小设置,一般建议在[0.6,1.0] 之间为宜。
粒子的最大速度VMAX与ω共同配合,对粒子群算法的性能具有影响。当最大速度VMAX较小时,ω近似为1,粒子群算法性能较好;当最大速度VMAX较大时,ω为0.8,粒子群算法性能较好。
2.3.3 学习因子
C1和C2用来控制粒子自身的记忆和同伴粒子记忆之间的相对影响。选择合适的学习因子值,可以提高算法速度,避免陷入局部极小值。普遍认为C1=C2=2是较好的选择,但试验证明了C1=C2=0.5也能得到较好的结果,能够避免陷入局部极小值。
2.3.4 算法过程
(1)初始化。
设置算法运行过程中的惯性因子ω,最大迭代次数nb_iterations,粒子群规模numberOfParticle。随机初始化第i个粒子的向量Xi={Xi1,Xi2,…,Xin}和每个粒子的初始速度VI={Vi1,Vi2,…,Vin},并设置当前迭代次数no_iteration为0。
(2)迭代。
如果no_iteration≥nb_iterations,则跳转至步骤(5)。否则,对于当前粒子群中的每个粒子执行如下步骤。
①使用3.3.1中描述的方法用粒子的学习后的位置next_location值更新粒子的当前位置current_location;按照式(1)~式(2)计算目标函数值。
②如果当前计算出的目标函数值小于该粒子的局部最优解,则用当前粒子的位置更新以前的局部最优解。
(3)更新全局最优解。
求得numberOfParticle个粒子中式(1)的目标函数值最小的粒子,根据该粒子的信息更新全局最优解。
(4)本次迭代完毕,即:
no_iteration= no_iteration +1
(5)得出结果,即求得全局最优解并输出。
3 试验结果与分析
试验采用4台普通的服务器搭建的Hadoop集群系统环境,每台计算机内存2 GB,磁盘空间250 GB。Hadoop的版本是hadoop.0.20.2。操作系统的版本是Red Hat Linux 9.0。试验所采用的测试方法为利用Hadoop进行WordCount 计算,并分别与默认Hadoop和文献[4] 中的方法进行比较。
数据分区是否均衡可以通过运行时间进行比较和评价。本节使用Reduce函数实现PageRank算法,比较第1轮的运行时间。
试验结果对比如图1所示。
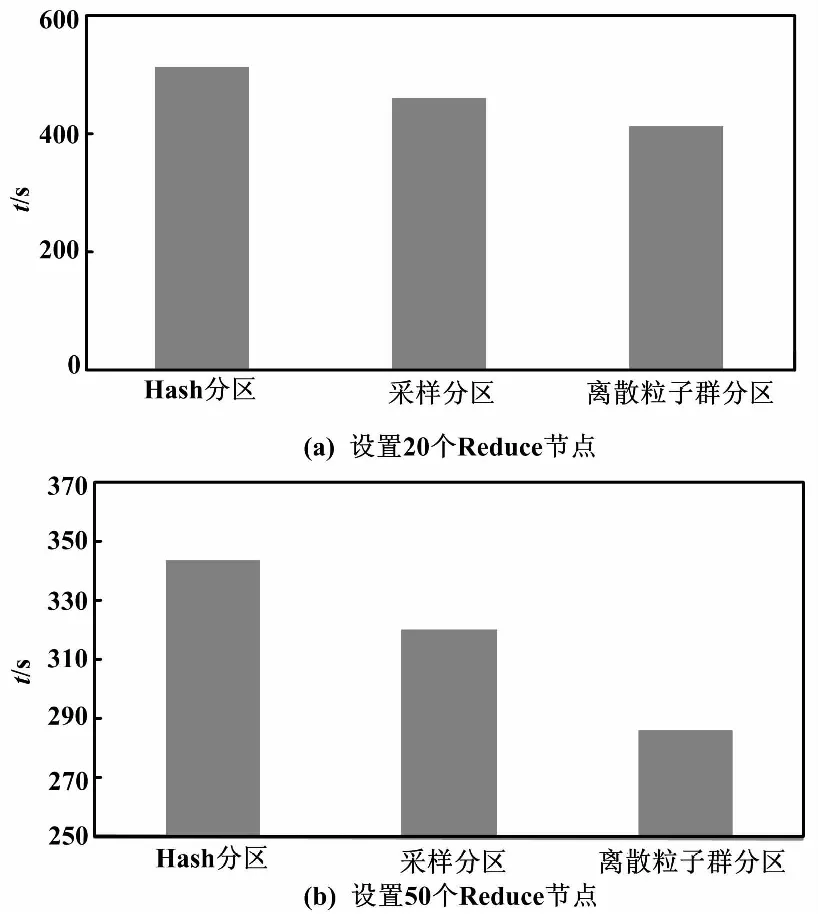
图1 试验结果对比图
由图1可见,当设置两种不同数量的Reduce时,在三种分区方式中,离散粒子群分区方式的运行时间均为最短,可以证明其解决数据分区的不平衡问题都比较有效。随着Reduce数量的上升,离散粒子群分区方式的优势更为明显。
本文还试验了离散粒子群算法中迭代次数参数的选择对数据运行时间的影响,设置Reduce数目为20个,如图2所示。

图2 迭代次数对运行时间的影响
从图2可以看出,当迭代次数超过第一阈值(如迭代300次)时,在此阈值基础上,随着迭代次数的增加,运行时间的缩短趋势较快,说明离散粒子群学习的结果较为准确,可获得相对较优的解。在迭代次数接近第二阈值(如迭代500次)时,运行时间并未显著缩短,说明离散粒子群算法寻找的较优解已接近稳定。
4 结束语
本文研究了采用MapReduce模型解决数据平衡问题,并基于智能计算的数据平衡方法进行最优解的计算求解。试验结果表明,与传统的Hash划分和预处理输入数据再制定分区策略相比,本文提出的基于离散粒子群算法的数据平衡方法更为高效。
后续研究将采用其他的智能算法(包括人工蜂群算法、鸟群算法)解决数据不平衡的特征,并将深入探索结合多种智能算法,以解决数据不平衡问题。
