基于UKF-LSSVM的燃煤机组NOx排放浓度预测方法

张友卫，曹硕硕，魏 威，李春岩，曾令超，杨晨琛，李益国

(1.江苏方天电力技术有限公司，江苏 南京 211102；2.东南大学能源与环境学院，江苏 南京 210096)

0 引言

随着节能减排政策的大力推行，氮氧化物的排放越来越受到环保部门的重视。目前，燃煤机组广泛采用选择性催化还原(selective catalyst reduction,SCR)脱硝技术。对NOx排放浓度进行准确预测，不但有利于进一步提高SCR控制系统的调节性能，而且可以用来判断现场数据是否真实准确，为环保部门的监管执法提供依据。由于脱硝系统十分复杂，且各参数变量间耦合关联严重，建立准确的机理模型存在很大困难。随着分布式控制系统的广泛应用，大量运行数据被记录下来，为数据驱动的脱硝系统建模和NOx排放浓度预测提供了可能。

秦天牧等[1]提出将改进偏互信息变量选择方法与支持向量机结合，进行火电厂SCR脱硝系统建模。Irfa M F[2]等采用人工神经网络(artificial neural network,ANN)对硫化床反应器SCR系统进行了建模和优化。但这些方法都属于离线建模方法，不具备对脱硝系统特性变化和煤质变化等因素的自适应能力。

针对上述问题，文献[3] 结合迭代策略和约简技术，提出一种在线自适应迭代约简最小二乘支持向量机。其通过寻求对目标函数贡献最大的样本作为新增支持向量，提高了在线预测精度。文献[4] 针对最小二乘支持向量机模型精度不足的情况，设计了样本更新策略，并避免了在线矩阵求逆，从而降低了在线计算量。上述在线算法存在的最大不足在于，对模型精度具有重要影响的核参数σ仍然只能通过反复试凑的方法离线确定，无法实现在线更新。

为此，本文提出了一种基于无迹卡尔曼滤波在线最小二乘支持向量机(unscented Kalman filter-least squares support vector machine,UKF-LSSVM)的燃煤机组NOx排放浓度预测方法。该方法能够同时在线更新σ和其他模型参数α、b。通过与最小二乘支持向量机(least squares support vector machine,LSSVM)的预测结果对比，证明了该方法的有效性。

1 基于无迹卡尔曼滤波最小二乘支持向量机

1.1 最小二乘支持向量机

假设训练样本集T={(x1,y1),(x2,y2),…,

(xN,yN)}。其中，xi∈Rn,yi∈R,i=1,2,…,N,N为训练样本的个数。为了在高维特征空间内构造最优决策函数f(x)=wTφ(x)+b，将问题转化为求解最小化结构风险：

(1)

yi=wTφ(xi)+b+eii=1,2,…,N

(2)

式中:w、b为模型参数；c为惩罚因子；φ(xi)为从输入空间到高维特征空间的非线性映射；ei为预测误差。

与之对应的Lagrange函数为:

(3)

式中：α=[α1α2…αN] 为Lagrange乘子。

根据最优化Karush-Kuhn-Tucker(KKT)条件:

(4)

联立Lagrange函数式(3)和KKT优化条件式(4)，得到最优化问题的线性方程组：

(5)

其中:

(6)

(7)

y=[y1y2……yN]T

(8)

(9)

式中：K(xi,xl)=〈φ(xi),φ(xl)〉为核函数。

联立式(5)和式(9)，求出最优决策函数为[6]：

(10)

1.2 无迹卡尔曼滤波

卡尔曼滤波是对线性系统状态进行最优估计的算法。对于非线性系统，则需要对非线性系统进行近似线性化，目前使用较多的是扩展卡尔曼滤波(extended Kalman filter,EKF)和无迹卡尔曼滤波(unscented Kalman filter,UKF)。对于非线性较强的系统，EKF近似线性化产生的误差会使滤波器的性能下降甚至发散；而UKF不引入线性化误差则不会出现这种问题，且该算法复杂程度低于EKF。因此，本文选择UKF进行动态模型核参数σ和模型参数α、b的估计[7]。

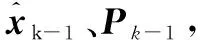
利用UKF进行参数估计的步骤如下。

①初始化。

(11)

(12)

②关于y的统计信息，可以通过δ点构成的矩阵x∈R2d+1产生：

(14)

(15)

(16)

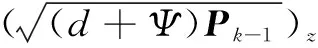
③时间更新。

xz,k|k-1=F(xz,k-1)

(17)

(18)

(19)

yz,k|k-1=G(xz,k|k-1)

(20)

(21)

④量测更新。

(22)

(23)

(24)

(25)

(26)

1.3 基于UKF的在线最小二乘支持向量机

鉴于无迹卡尔曼滤波在参数估计中的优良性能，将其引入在线最小二乘支持向量机算法，以确定模型参数α、b和核参数值σ[8]。

引入多维的参数向量：

(27)

重新组织方程，可以得到：

(28)

UKF-LSSVM建模流程如图1所示。

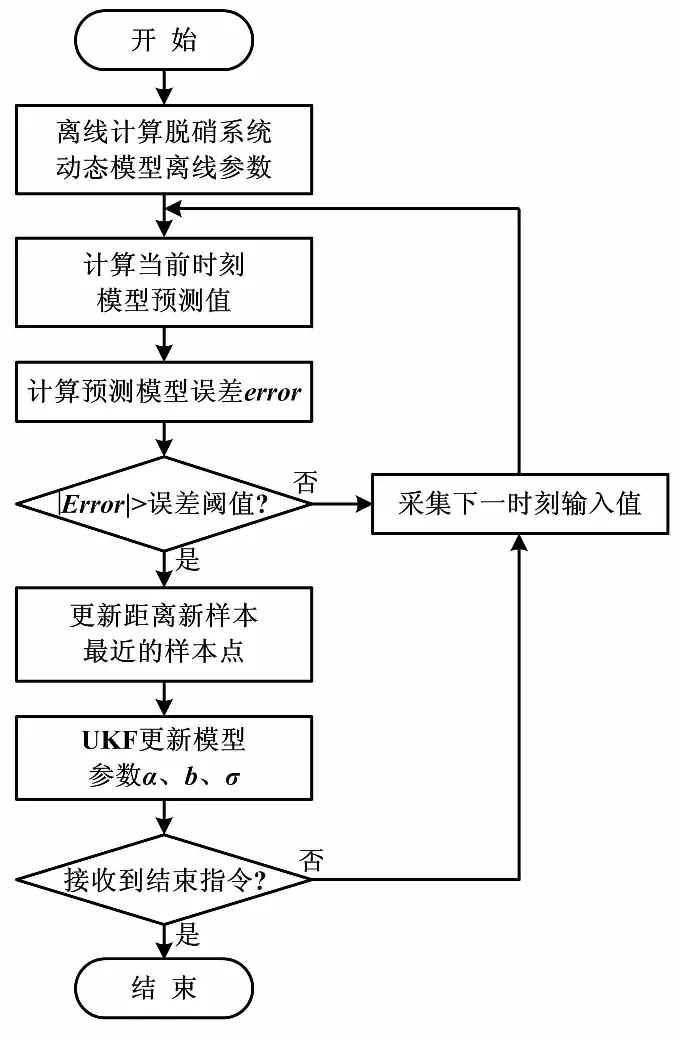
图1 UKF-LSSVM建模流程图

2 NOx排放浓度预测方法

2.1 数据采集和预处理

本文以某300 MW燃煤锅炉SCR脱硝系统为研究对象。建模数据跨度为一个月，采样周期为5 s，包含稳态数据和动态变负荷的数据。测点包括烟囱入口NOx浓度、甲、乙两侧喷氨阀门位置、两侧喷氨流量、反应器进口NOx浓度、机组负荷等。

建立NOx预测模型之前，首先对相关数据进行如下预处理。采用式(29)，将样本数据全部归一到[0,1] 之间：

(29)

式中：x、x′分别为归一化前后样本值；xmin、xmax为样本数据中的最小值和最大值。

2.2 NOx预测模型结构

根据Pearson相关系数[9]检验变量间联系的紧密程度，同时分析影响NOx排放浓度的主要因素。选定模型输入为：两侧喷氨流量、两个反应器进口NOx浓度和机组负荷。由于环保考核以烟囱入口测点为依据，因此将烟囱入口NOx浓度作为模型的输出变量。

需要说明的是，在建模过程中，考虑了输入和输出变量的阶次，从而使得该模型可以实现对变负荷动态过程的NOx排放浓度预测。

脱硝系统动态模型结构如图2所示。

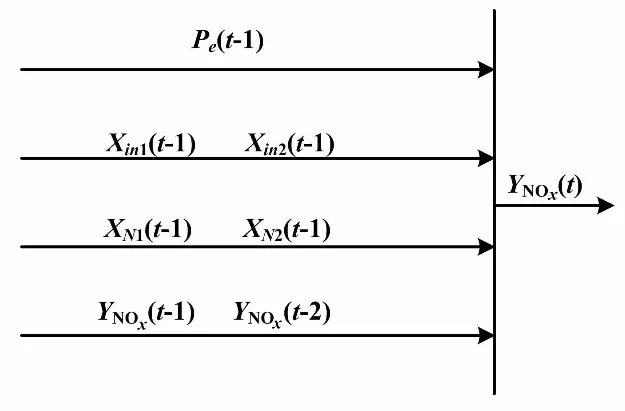
图2 脱硝系统动态模型结构图

图2中：Pe(t-1)为机组负荷；xin1(t-1)、Xin2(t-1)为两侧SCR反应器入口NOx浓度；XN1(t-1)、xN2(t-1)为两侧喷氨量；YNOx(t-2)、YNOx、YNOx(t)为不同采样时刻烟囱入口的NOx浓度。

2.3 预测结果及分析

选取5 000个负荷变动情况下的样本点进行建模仿真。以样本集的前50个样本作为初始训练样本。选用均方根误差(root mean squaied error,RMSE)和平均绝对百分比误差(mean absolute percentage error,MAPE)[10]来评价预测模型的精度，计算公式为：

(30)

(31)

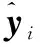
为说明UKF-LSSVM方法的有效性，将其与批量LSSVM算法进行比较，参数σ经过多次试验取为3。2种方法的预测值和真实值的对比和预测误差结果分别如图3、图4所示。

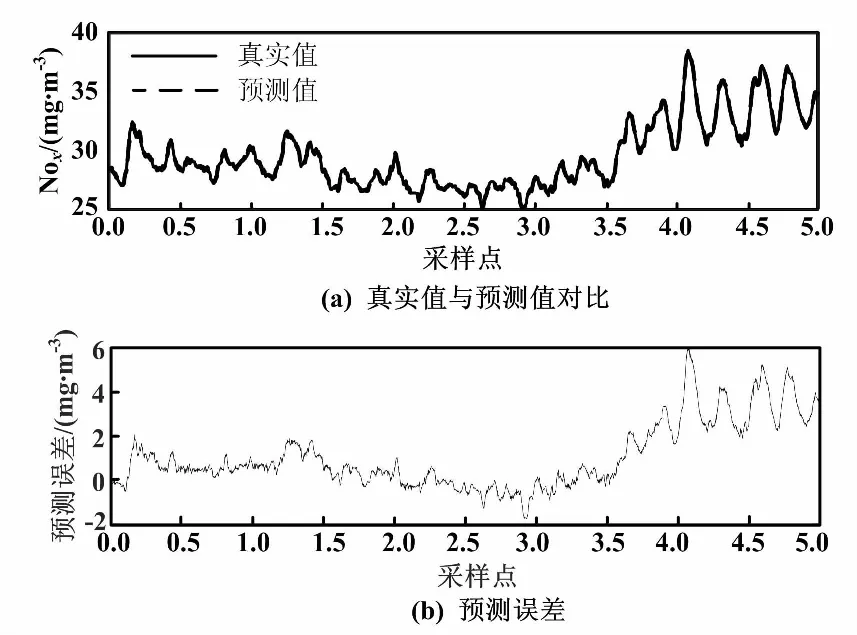
图3 批量LSSVM模型预测结果(σ=3)

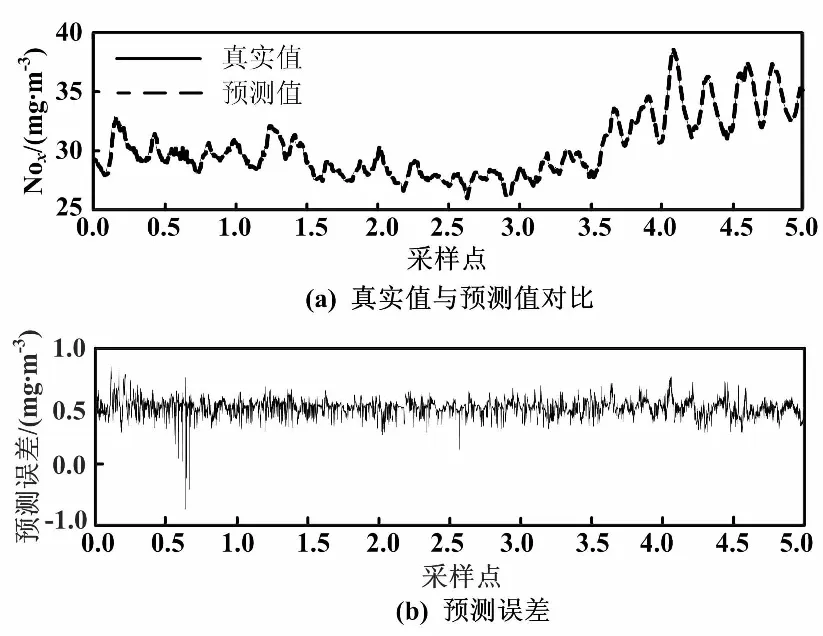
图4 UKF-LSSVM模型预测结果(σ=3)

当σ=3时，2种方法对5 000组数据的预测精度对比如表1所示。

表1 不同模型精度对比

由图3、图4和表1可以看出，批量LSSVM方法由于不具备自适应更新能力，因此仅能在与训练样本相似的工况下取得较好的预测效果。而对于偏离训练样本较大的情况，预测偏差将显著增大。与之相比，UKF-LSSVM能根据预测偏差的大小，在线修正模型参数，因而始终具有较高的预测精度。

为检验UKF-LSSVM在核参数σ修正方面的优势，将初始核参数σ设为0.1，并进行仿真试验。UKF-LSSVM模型预测误差和核参数σ变化情况如图5所示。

图5 UKF-LSSVM模型预测结果(σ=0.1)

当初始核参数σ为0.1时，UKF-LSSVM模型的均方根误差为0.068 3 mg·m3，平均绝对百分比误差为0.16。从图5可以看出， UKF-LSSVM对于任意给定的核参数初值，依然取得了很好的预测结果。其模型精度不受σ的影响，从而大大降低了σ的选取难度，对该方法的实际应用具有重要作用。

3 结束语

本文提出了一种基于无迹卡尔曼滤波最小二乘支持向量机的NOx排放浓度预测方法。该方法能够同时在线更新核参数σ和其他模型参数α、b。围绕某300 MW机组脱硝系统进行NOx排放浓度建模，并与批量最小二乘支持向量机的仿真结果进行对比，验证了该方法具有很高的NOx预测精度和自适应能力。该方法不仅有利于环保部门对燃煤电厂机组的污染物排放进行实时监控，同时也可与先进控制方法相结合，提高脱硝系统的运行效率，保证电厂运行的经济性和环保性。