基于MI-LSSVM的NOx生成量动态软测量模型

赵 征，袁 洪，宋选锋

(华北电力大学控制与计算机工程学院，河北 保定 071003)

0 引言

火力发电是中国的主要发电方式，燃煤锅炉中煤炭燃烧产生的氮氧化物已成为污染环境的主要因素[1-2]。烟气在线监测系统存在的测量滞后问题，会导致脱硝系统控制效果不理想。软测量是解决该问题的一种有效方法。

目前，传统NOx生成量的软测量方法大多使用静态建模，即当前时刻的输出只与当前时刻的输入有关。而在实际机组运行过程中，输入、输出变量之间存在明显的时间滞后，如燃料运送过程产生的时延、信号的测量延迟等[3]，导致建模时在同一时间上所选的输入输出数据不匹配，静态建模无法满足实际需求。对此，学者们提出了各种算法。文献[4] 、文献[5] 使用递归最小二乘的方法，估计出辅助变量的迟延；但这种方法存在一定的局限性。文献[6] 通过相关系数，分析了辅助变量与主导变量间的时延；但这种方法不适用于非线性过程。

鉴于互信息适用于非线性过程的时延估计，提出基于最小二乘支持向量机(least squares support vector machine,LSSVM)与互信息(mutual information,MI)的NOx生成量动态软测量方法。首先，通过主成分分析(principal component analysis，PCA)选择辅助变量；然后，采用互信息方法确定各辅助变量的时间迟延；最后，引入过去时刻的输出作为当前时刻模型的输入，以适应工业过程的动态性。将包含过程时延信息和动态信息的新数据集作为模型的输入，基于LSSVM建立NOx生成量的动态软测量模型。采集某电厂330MW机组的一段历史运行数据，对模型进行验证。验证结果表明：该模型的预测值超前于LSSVM静态模型的预测值，具有良好的预测效果。

1 最小二乘支持向量机

最小二乘支持向量机是在支持向量机(support vector machine，SVM)的基础上演变而来。在求解线性方程组的问题上，由于LSSVM引入最小二乘线性系统时使用了二次规划方法解决问题，有效避免了SVM的复杂计算[7]。

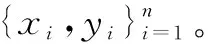
yi=f(xi)=〈w,φ(xi)〉+b

(1)

式中：〈,〉为点积；w为权重向量；φ(xi)为原始变量数据映射以后的值；b为偏差。

LSSVM优化问题可转化为：

(2)

式中：ζi为误差变量；c为惩罚参数。

利用目标函数和约束条件，建立拉格朗日函数：

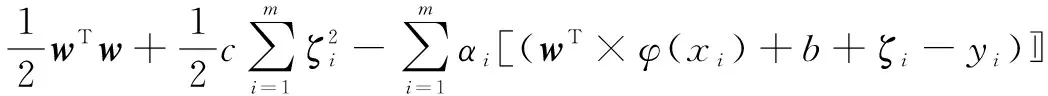
(3)

式中：αi(i=1,2,…,m)为乘子。

(4)

(5)

式(4)的另一种表示方式为：

(6)

式中：I=[1,2,…,l]T;L为m×m阶单位矩阵；Ωij=φ(xi)Tφ(xj)=K(xi,xj)为核函数；α=[α1,α2,…,αm]T为乘子；y=[y1,y2,…,ym]T。计算LSSVM估计函数的公式为：

(7)

式中：K(x,xi)=〈φ(x),φ(xi)〉为核函数。

(8)

2 互信息

互信息方法可以计算2个变量之间的关联性，从而可应用于计算复杂生产过程中辅助变量与目标变量的迟延时间。信息论中，熵可以度量变量间的不确定性，设X、Y为2个变量，X的概率密度分布函数为μ(x)，则变量X的熵表示它的不确定性[9]，定义为：

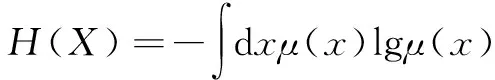
(9)

由此可得互信息定义为：

(10)

式中：μ(x,y)为X、Y的联合概率密度；μx(x)、μy(y)分别为X、Y的概率密度分布函数。

根据熵的定义，互信息的计算可表示为：

MI(X,Y)=H(X)+H(Y)-H(X,Y)

(11)

互信息越大，表明变量X包含关于变量Y的信息越多。

以概率密度估计为基础的直方图法、核方法，在计算高维数据时的可靠性与估计精度会降低，不适用于高维数据计算[10]。而K-近邻互信息估计方法有效避免了直接进行概率密度估计，简化了高维互信息的计算。

K-近邻互信息算法思想为：在X、Y构成的空间Z=(X,Y)中，将每一个点Z(i)=(Xi，Yi)与其他点的距离进行排序。设0.5εi为点zI=(xi,yi)到其K-近邻的距离，0.5εx(i)为点zi=(xi,yi)到X轴上的相应点的距离，同理可得0.5εy(i)。

统计可知，点xi的距离小于0.5ε的样本点数目nx(i)。对变量yi作相同的处理得到ny(i)，通过式(11)计算变量X与Y之间的互信息。

MI(X,Y)=φ(k)-〈φ(nx+1)+φ(ny+1)〉+

φ(N)

(12)

则m维变量(X1,X2,…,Xm)之间的互信息为：

MI(X1,X2,…,Xm)=φ(k)-〈φ(nx1)+…+φ(nxm)〉+(m-1)φ(N)

(13)

燃煤机组NOx的生成量影响因素众多，而单变量互信息(single variable MI，SMI)只考虑到了单个变量与主导变量之间的关系。因此，采用式(14)，将可以计算出每个辅助变量对NOx的生成量的信息贡献。

MI(x1,x2,…,xm;y)=MI(x1,x2,…,xm;y)-

MI(x1,x2,…,xm)

(14)

3 基于LSSVM的动态软测量模型

通常，电站锅炉采集的NOx测量值y(k)与辅助变量在时间上存在滞后关系，使模型的输入输出在k时刻并非一一对应。当前k时刻的y(k)值往往与辅助变量di时刻之前的历史数据xi(k-di)有关。其中：di是辅助变量xi的时间延迟。实际生产过程中，y(k)的值还与自身前几个时刻的值有关。因此，本文采用 LSSVM 与互信息相结合的软测量方法，对NOx的生成量进行预测。动态软测量模型结构如图1所示。

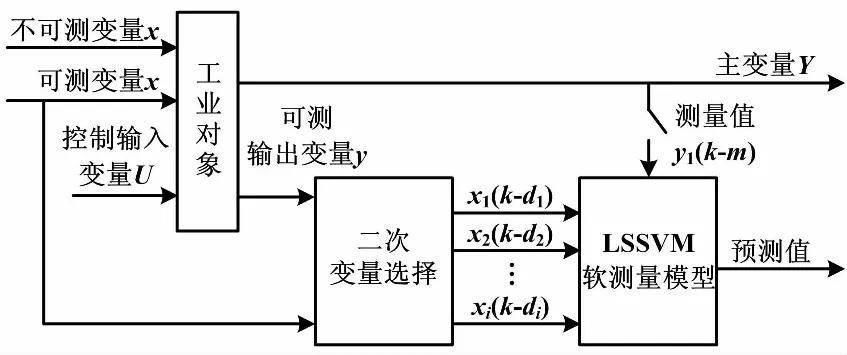
图1 动态软测量模型结构图

图1中：U为对象的控制输入；y为对象的可测输出变量；y1为实际测量值。

该动态软测量模型的建模步骤如下。

①通过PCA方法，选择影响燃煤机组NOx生成量的主要因素。

②采用互信息的方法，确定各辅助变量xi的时延估计值di，并根据经验得出NOx生成量测量数据的迟延m。

③把含有工业过程的动态时延信息引入软测量模型。即使用信息集{xi(k-d1),x2(k-d2),…,xi(k-di),y(k-m),y(k)}，建立最小二乘支持向量机模型。

其中：模型输入的选取与训练样本数据的预处理是整个方案实现的前提；时间迟延的确定与LSSVM模型的建立是整个方案的关键。

3.1 NOx 生成量的辅助变量选择

通过文献[11] 、文献[12] 及NOx的生成机理，初步确定辅助变量为二次风总风量、总煤量、总风量、各层二次风挡板开度、烟气温度和烟气含氧量。根据所确定的14个辅助变量，采集某电厂330 MW机组厂级监控信息系统(supervisory information system，SIS)中的实际运行数据，采样间隔为10 s，共7 150组数据点。将前6 900组数据作为模型训练，后250组数据作为模型测试。

采用拉依达法则对原始历史数据存在的异常值进行预处理，使处理后的数据更具完整性和准确性，并通过归一化使样本处于同一量纲。利用相关性分析得到输入变量间的Pearson相关系数如图2所示。

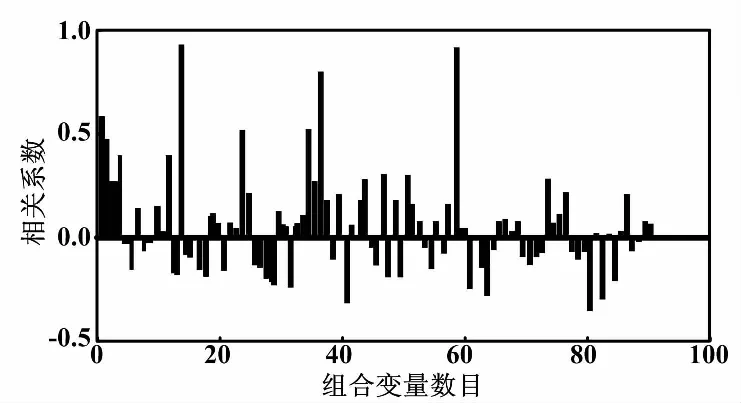
图2 Pearson相关系数

由图2可知，各个变量之间存在正相关或负相关，若将所有辅助变量作为输入进行建模，会增加模型的复杂度。使用PCA进行变量选择，可以删除冗余的辅助变量，降低了模型的复杂程度。经过PCA后的主成分贡献率及累计贡献率如图3所示。

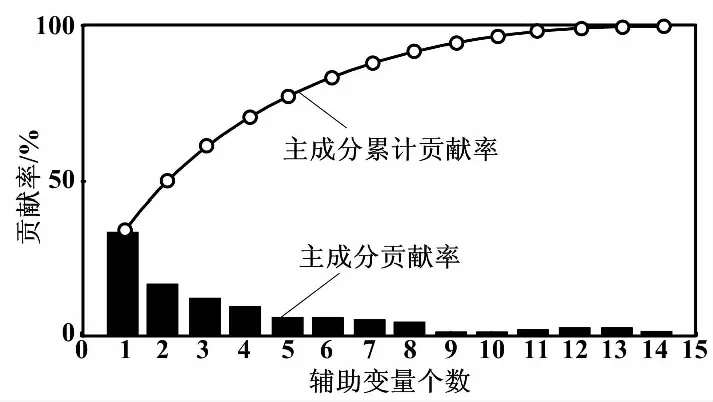
图3 主成分贡献率及累计贡献率

设累计贡献率的要求为80%，选择前4个主元进行分析，依次计算每个主元的载荷，最终确定所选的辅助变量。通过载荷计算，主元1的得分如图4所示。

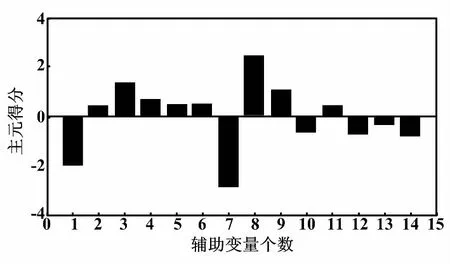
图4 主元1得分

由图4可知，在主元1得分较高的变量序号为1、7与8，其代表的变量分别为总煤量、D层与E层二次风挡板开度。通过计算4个主元上的主元得分率最终所选辅助变量为：总煤量、总风量、A层、B层、D层、E层和AA层二次风挡板开度。

通过计算互信息MI，以当前k时刻的y值依次向前搜寻d时刻与y值最大的互信息量，d即为各辅助变量的迟延时间。各辅助变量的时间迟延di如图5所示。

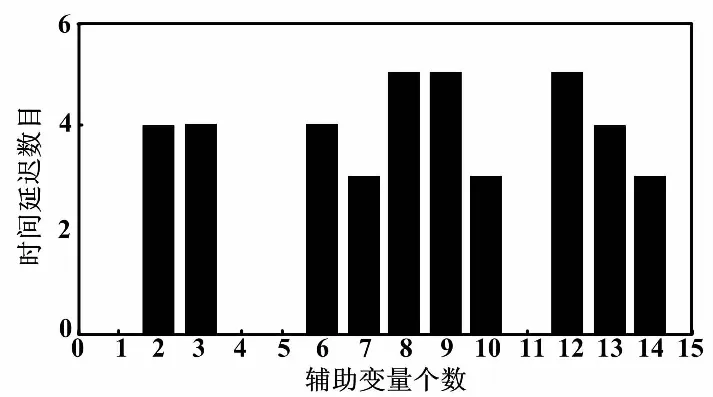
图5 各辅助变量时间迟延

根据实际情况，估计出脱硝系统入口NOx测量值存在20～70 s滞后。将测量迟延与图5得出的时间迟延引入到模型的输入，确定最终的输入变量集为:{x1(k),x2(k-4),x3(k-4),x4(k),x5(k),x6(k-3),x7(k-5),x8(k-5),y(k-3)}。

3.2 建立LSSVM的动态软测量模型

通过以上输入变量集，建立LSSVM的动态软测量模型。训练模型对比及局部放大图如图6所示，测试模型对比如图7所示。

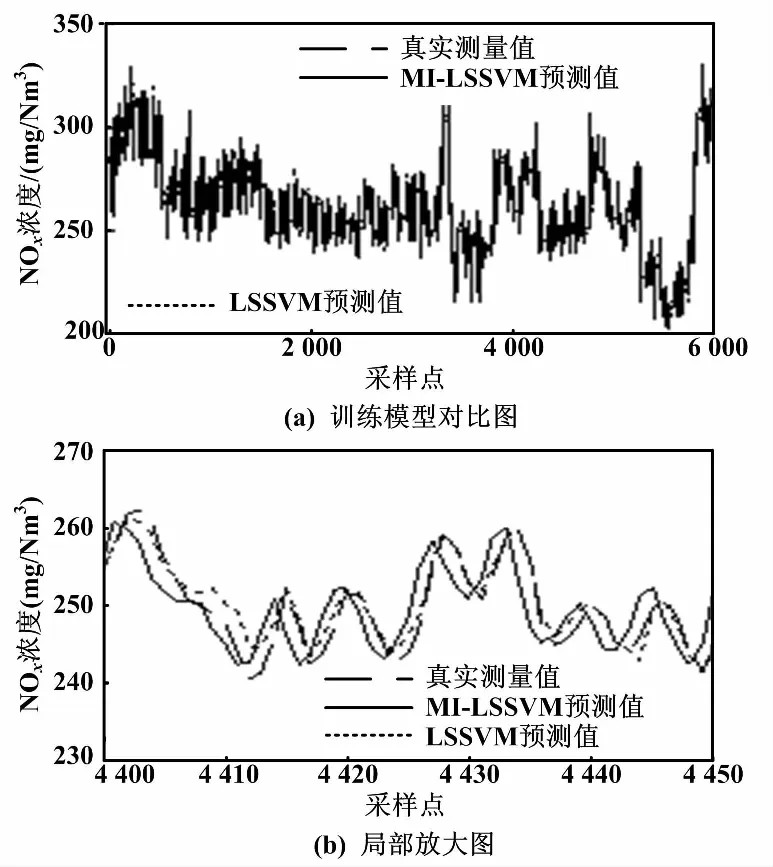
图6 训练模型对比图及局部放大图

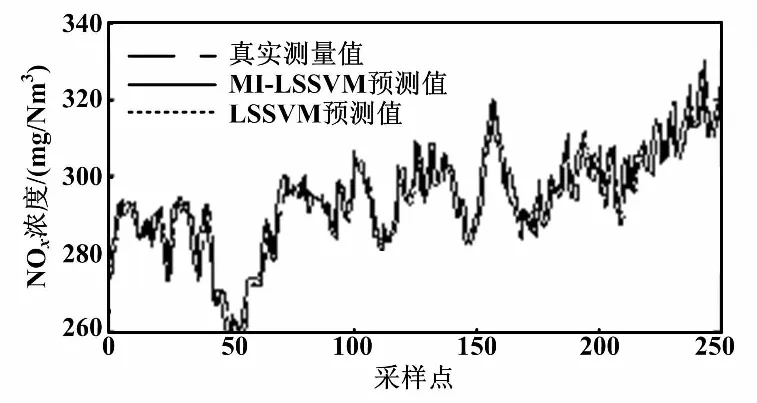
图7 测试模型对比图

从图6和图7可以看出，基于MI-LSSVM模型比单独使用LSSVM的预测结果超前约1～2个采样点(10～20 s)。

基于MI-LSSVM的模型与单独使用LSSVM的预测误差的对比如表1所示。

表1 不同模型预测误差对比

由表1可以看出，基于MI-LSSVM模型的平均相对误差和均方根误差均低于单独使用LSSVM的误差，而且决定系数有明显提高，表明基于MI-LSSVM模型具有更好的泛化能力。

本文所建立NOx生成量的动态软测量模型中，测试模型较训练模型误差偏大。这主要与选择训练样本的数量、辅助变量、涵盖的工况以及测试样本的数量有关，同时还与延迟时间的准确性有关。如果能够在每个环节都做到详细而精确的测量，就能相对提高测试模型的误差。

4 结束语

最小二乘具有较好的泛化能力以及互信息能力，适用于高维数据变量问题的选择。本文提出基于MI-LSSVM的燃煤机组NOx生成量动态软测量模型。首先，分析了影响燃煤机组NOx生成量的因素。其次，通过互信息确定了各辅助变量的时间迟延与历史数据长度。最后，将包含过程时延信息和动态信息的新数据集作为LSSVM的输入建立模型。

MI-LSSVM模型与LSSVM模型的预测结果对比表明：将过去时刻的输入、输出数据作为当前时刻模型的输入，提高了模型的动态性，使模型的预测值超前于单独使用LSSVM的预测值。另外，迟延时间的确定提高了模型的预测精度，证明了该方法的有效性。