机器学习在批次生产过程操作寻优中的应用

韩晓春，田 甜，吴学华，娄海川，吴玉成，侯卫锋

(浙江中控软件技术有限公司，浙江 杭州 310053)

0 引言

由于石化工业生产机理的复杂性、生产模式的不断变化、设备状况的老化及生产过程的扰动等原因，常常使生产偏离优化状态，产品质量降低。化工批次生产过程的产品质量主要取决于操作参数和原料，在供给原料相同的条件下，操作参数的调整将直接影响产品品质的稳定性。因此，需随时对操作参数进行适当调整，以保证产品质量。一般情况下，现场工艺人员会结合化验分析结果和操作经验调整生产操作参数，而化验分析结果通常滞后于实时生产，难以根据原料变化和产品的规格要求将操作参数及时调整到相应的最优状态。针对过程操作参数优化问题，大量学者进行了深入研究，力求在现有设备、原料和工艺流程不变的条件下，通过优化过程操作参数提高产品质量[1-3]。

为提高产品品质，本文给出基于机器学习算法进行工艺参数寻优的方法，寻求批次生产操作参数的最优组合，并结合参数建议值和操作经验对工艺操作作出相应调整。

1 操作寻优有关算法

1.1 随机森林

随机森林[4]采用Bootstrap[5]重采样技术，以K个决策树{h(X,θk),k=1,2,…,K}为基学习器，进行集成学习后得到组合模型。其中，参数{θk,k=1,2,…,K}是独立同分布的随机向量。在给定样本时，通过每个决策树的输出结果投票来决定随机森林的最优预测结果[6-7]。

随机森林可以用于分类和回归。针对分类问题，因变量为分类变量，组合方法是简单多数投票法；针对回归问题，因变量是连续变量，则是简单加权平均法。大量的理论和试验都证明了随机森林简单易实现，计算开销小，具有很高的预测准确率，对异常值和噪声具有较好的稳定性，且不易产生过拟合，具有较强的泛化能力。

随机森林回归算法的步骤如下。

①采用Bootstrap重复抽样法，从原始样本集中随机采样，产生K个训练样本集{θ1,θ2,…,θK}。

②从所有特征中随机选择m个特征作为当前节点的分裂特征集，利用这些特征进行决策树[8]建模，选择最好的特征方式对节点进行分裂。

③不对任何决策树进行剪枝处理，使其最大限度地生长。

④对K个训练样本集进行学习，重复以上步骤K次，即生成K棵决策树{T(θ1),T(θ2),…,T(θK) }，形成随机森林。

⑤对于新样本数据x，单个决策树T(θ)的预测值可通过因变量的观测值Yi(i=1,2,…,n)的加权平均得到，即：

(1)

式中：wi(x,θ)为决策树权重向量,i=1,2,…,n，满足∑wi(x,θ)=1；

⑥对决策树权重wi(x,θ)(i=1,2,…,n)取平均，得到每个观测值Xi(i=1,2,…,n)的权重：

(2)

⑦经过每棵树决策，对于所有y，随机森林的最终预测值为所有因变量观测值的加权和：

(3)

1.2 Mean Shift聚类

Mean Shift算法是一个非参数聚类技术，不需要预先确定聚类的类别数，且可以根据数据的特征发现任意形状的聚类簇。

给定d维空间的n个数据点集{xi,i=1,2,…,n}，对于空间中任意点的Mean Shift向量，其基本形式可以表示为：

(4)

式中：k表示在这n个样本点中，有k个点落入Sh区域中；(xi-x)表示样本点xi相对于原点x的偏移向量；Sh为以h为半径的高维球。

Sh(x)={y|(y-xi)T(y-xi)≤h2}

(5)

对于基本的Mean Shift向量，可以增加核函数和样本权重，从而得到改进的Mean Shift 向量形式[9]进行聚类分析。Mean Shift聚类步骤如下。

①从未被标记的数据集中，随机选取点x作为初始中心点，在指定的区域Sh内计算出偏移均值。

②更新球圆心x的位置x←x+Mh。

③重复步骤①和步骤②，直至满足条件||Mh||<ε。记此时的球圆心x为簇中心点，将区域Sh内的点都标记并划入该簇中。

④如果收敛时当前簇ci+1的中心与其他已存在的簇ci中心的距离小于阈值，那么将两类簇合并；否则，把ci+1作为新的聚类。

⑤重复步骤①～步骤③，直至所有点都被标记，得到簇划分c1,c2,…,cn。

2 机器学习算法进行操作参数寻优

基于机器学习算法进行批次生产过程操作参数优化的步骤如下。

①获取产品品质要求的实验室信息管理系统(laboratory information management system,LIMS)化验分析数据进行频次图分析，根据过程能力指数(capability index of process,Cp/Cpk)和过程性能指数(performance index of process,Pk/Ppk)判断批次生产过程是否稳定操作，品质要求是否控制在合理范围内。

②通过人工录入批号，将产品品质要求的化验分析数据与实际生产操作进行匹配，结合现场工艺人员的操作经验，选择可能影响产品品质的工艺过程参数。

③将化验分析数据和工艺过程参数进行归一化处理，分析其关联性，选择重要的特征参数。

④采用随机森林算法进行数据拟合建模。

⑤计算出指定范围内工艺操作参数组合对应的产品品质拟合值，通过网格搜索找到产品品质要求范围内的所有工艺操作参数组合。

⑥对找出的工艺操作参数进行Mean Shift聚类分析，自动寻找合适的工艺操作参数组合。

机器学习算法在批次生产过程操作参数优化的流程图如图1所示。

图1 操作参数优化流程图

3 实例分析

某工厂生产107胶，原料是水解物，生产过程主要包含脱水、聚合和脱低3个工艺过程。由于对产品的黏度要求较高，根据不同的黏度规格，其生产操作参数的控制不同，现场工艺人员必须通过调节充氮气时间、聚合时间和聚合温度等操作参数，控制产品黏度值。由于缺乏定量的操作指标，控制效果并不理想，相同规格、不同批次的黏度差异较大。因此，迫切需要应用机器学习算法寻找最优工艺操作参数，对该厂的107胶产品进行黏度控制。

3.1 黏度频次图分析

107胶黏度检验结果如图2所示。

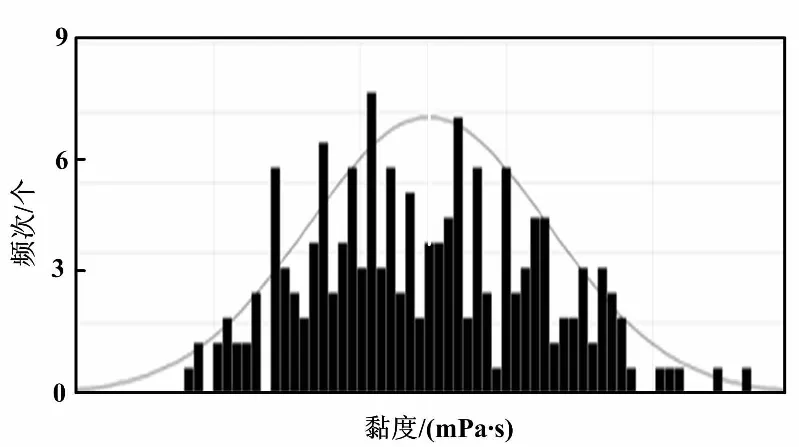
图2 107胶黏度检验结果

对107胶20 000黏度的LIMS化验分析数据进行正态分布检验。图2中，直方图表示107胶粘度的频次分布，曲线表示对应的密度曲线，可以直接反映出107胶黏度的分布情况。由图2可发现，黏度波动范围较大，不符合正态分布生产趋势。经过现场调研发现，一般情况下，在生产过程中，工艺人员并没有实时跟踪107胶的生产操作参数并进行调整，且不同班次的工艺人员依据经验来调整生产操作参数。这样虽不会超出工艺规程中的上下限，但生产操作参数并不是最优的，具有一定的优化空间。

3.2 工艺参数选择

影响107胶最终质量的关键过程工艺参数很多，包括能够实时测量的位号参数，以及需要从工艺单中提取的阶段性参数。结合实时位号趋势和工艺人员的经验，从中挑选了19个不同的工艺过程参数。

3.3 相关性分析

从实时数据库中提取某个月的107胶批次生产过程中的19个工艺参数，首先进行规范化预处理，即作如下变换。其目的是将工艺参数的值控制在[0,1] 之间。

(6)

对该19个工艺参数与对应的黏度进行相关性分析：

(7)

式中：Cov(X,Y)为X、Y的协方差；D(X)、D(Y)分别为X、Y的方差。

计算黏度与各工艺参数的相关系数，黏度与聚合时间和充氮气时间的相关系数较大，分别为0.49和0.47。由此可以推断，聚合时间以及充氮气时间是与黏度相关性最大的两个工艺过程参数。除此之外，根据90%相关度的原则，增加了脱水结束温度、压料结束温度、脱低结束温度3个工艺过程参数，由此提取出关联性较高的5个过程工艺参数。

3.4 数据建模与优化建议

提取出对建模最重要的5个过程工艺参数，并结合对应黏度值进行非线性数据建模，包括人工神经网络、支持向量机、随机森林等多种非线性拟合模型，从而挑选出最优拟合模型。利用3种非线性数据驱动模型对该批数据进行拟合建模，并从中找出最能表达这批数据内部规律的随机森林模型。以随机森林的高维拟合曲面为基础，以20 000上下5%的黏度值为限制条件，分别对归一化后的工艺参数数据进行10等分，对该参数空间进行网格搜索，寻找满足条件的参数组合。由于满足条件的参数组合很多，因此需要再对这些参数组合进行聚类分析，得到最优参数组合。此处通过Mean Shift聚类分析，找出了满足限制条件的两大类参数中心。工艺参数组合建议值如表1所示。

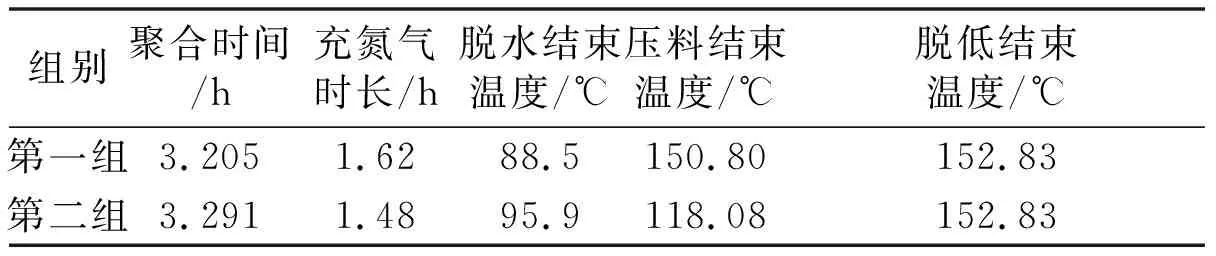
表1 工艺参数组合建议值

根据工艺人员的实际经验以及操作指导规程，脱水与聚合反应之间的压料温度不宜过低。通过对模型的训练数据集中的压料结束温度分布进行检验，发现大部分样本的压料结束温度分布在152 ℃，仅有较少样本的压料结束温度分布在122 ℃。因此，在实际生产过程中，只对第一组操作建议值进行了测试。

最后，将20 000黏度107胶的操作优化建议值与新建的虚拟位号相关联，并实时显示在工艺流程图上。工艺人员可以参考操作参数建议值，结合运行工况和现场实时数据及时调整参数，使产品的质量品质在可控范围内。

3.5 产品黏度控制效果对比

结合运行工况，工艺人员根据操作优化建议值对操作参数进行了调整，并对操作优化前和采用第一组操作优化建议值这两种运行状态下的控制指标进行对比分析，控制指标包括过程能力指数Cp/Cpk、最大值、最小值。107胶产品黏度控制测试结果如表2所示。

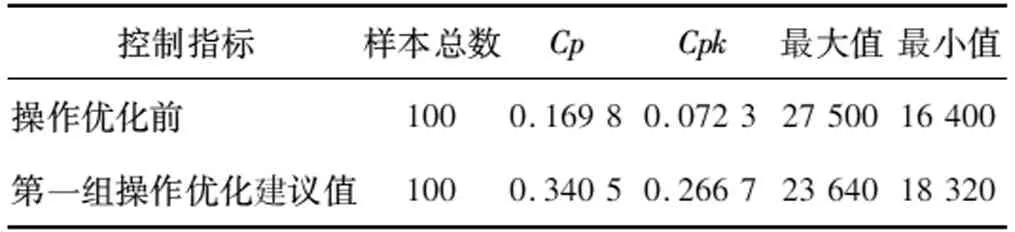
表2 107胶产品黏度控制测试结果

采用优化建议值后，Cp指标由0.169 8升到0.340 5，Cpk指标由0.072 3上升到0.266 7，极差(最大值-最小值)也明显减小。107胶质量控制结果可视化分析如图3所示。

最后，对质量控制结果进行了可视化分析。由图3可知，直方图通过给出每个值的频次来反映样本的分布规律，而密度曲线可以看出数据分布的密度情况。采用优化建议值后，可以发现20 000黏度值型号107胶的质量分布更加集中，说明了采用优化建议后，生产过程的质量控制能力有了较为明显的提升。

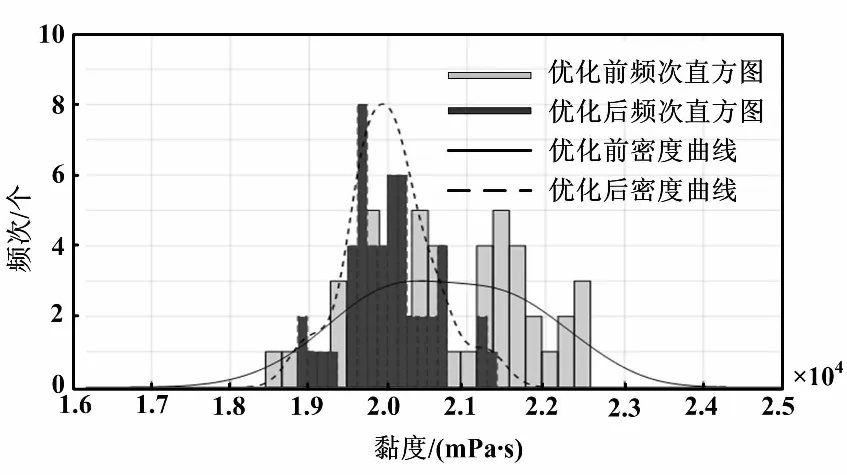
图3 107胶质量控制结果可视化分析

4 结束语

为了寻找批次生产过程中操作参数的最优组合、提高产品品质，本文提出了基于机器学习算法进行工艺操作参数寻优的方法。将该方法应用于某工厂20 000黏度的温室硫化甲基硅橡胶(107胶)生产中，可知：首先，通过人工录入批次、将LIMS化验分析数据与实际生产操作数据相关联；然后，根据产品黏度要求，应用机器学习算法寻求最优的操作参数组合；最后，由现场工艺人员结合参数建议值和操作经验作出相应调整，使产品的质量控制得到了明显改善。