基于传统ip-iq谐波检测方法的改进研究①

(安徽理工大学电气与信息工程学院，安徽 淮南 232000)

0 引 言

在科技飞速发展的今天，电能作为使用最为广泛的能源其质量的保证显得尤为最重要，而谐波的检测是提高电能质量的关键步骤，基于瞬时无功功率理论[1～3]的谐波检测是现阶段使用较多的检测方法之一，但在传统的基于瞬时无功功率理论的谐波检测方法中，由于低通滤波器[4]的存在，会使谐波检测的结果受到低通滤波器性能的制约，想要得到较高精度的检测结果，却要等待较长的检测时间。因此，如何克服滤波器所带来的缺陷对于快速，准确地检测谐波变得十分重要。下面阐述传统的基于瞬时无功功率理论的ip-iq[5]谐波检测方法，分析其不足并在其基础上进行改进。

1 传统的基于瞬时无功功率理论的ip-iq谐波检测方法

三相电路瞬时无功功率理论是由日本学者Akagi.H[6]于1983年提出，而ip-iq理论是以其为基础计算瞬时有功电流ip和瞬时无功电流iq的理论体系，其算法原理框图如图1所示[7]，图中PLL为锁相环，利用其对A相电压瞬时信号进行锁相得到与 A 相电压同频率、同相位的正余弦同步旋转信号[8]，并且通过Park变换和Clarke变换得到ip和iq，如公式(1)所示。

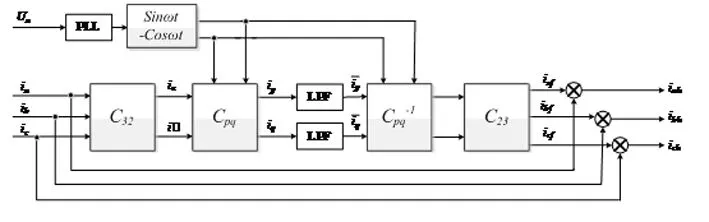
图1 传统ip-iq算法框图

(1)

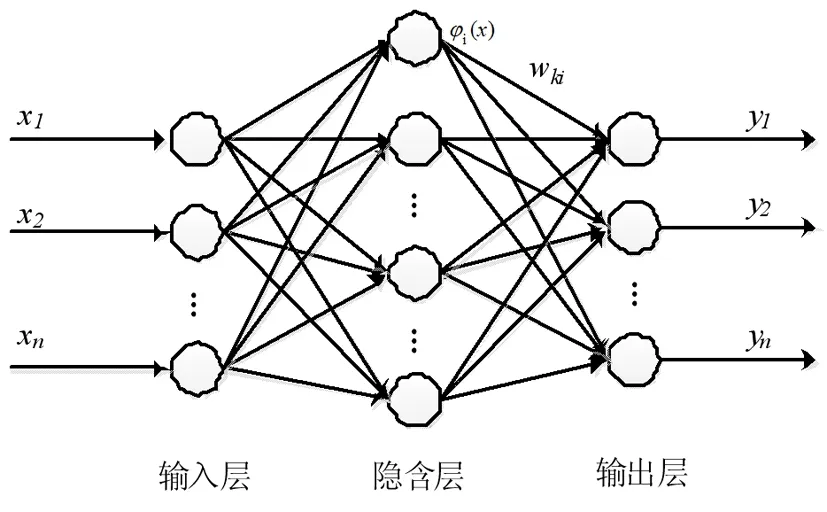
图2 RBF神经网络结构图

瞬时有功电流ip和瞬时无功电流iq经过LPF滤除高次谐波，得到直流分量和，经过Clarke和Park反变换可以得到基波正序电流分量，最后与三相电路电流相减，得到需要检测的谐波。如公示(2)、(3)所示

(2)

(3)

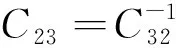
此种谐波检测方法中，低通滤波器选用的类型是Butterworth滤波器，检测结果受其截止频率和阶数两个因素影响，截止频率相同时，阶数越大，动态响应越慢，检测精度越高；阶数相同时，截止频率越大，动态的响应速度越快，检测精度降低。因此，选择合适的滤波器参数对谐波检测实时性和准确性至关重要。

2 传统ip-iq谐波检测算法的改进

为了克服前述传统ip-iq法中低通滤波器给检测结果带来的影响，得到更好的滤波效果，提出用RBF神经网络替代低通滤波器的一种改进策略来实现快速，精准滤波。

RBF神经网络，又称径向基函数神经网络，是一种性能优良的三层静态前馈型神经网络。输入层只是起到传递信号的作用，这样可以把输入矢量直接映射到隐含层，隐含层神经元的变换函数为径向基函数，是一种局部响应函数，第三层即输出层是对输入模式做出的响应，节点一般是简单的线性函数。RBF神经网络结构如图2所示。

RBF神经网络隐含层一般采用高斯函数作为激励函数，其形式见公式(4)：

(4)

式中x是网络的输入矢量；ci是第i个基函数的中心，与输入矢量x同维；σi为是第i个感知变量，决定基函数中心点的宽度，高斯函数体现了RBF神经网络的非线性映射能力，而隐含层到输出层的映射是线性的，即：

(5)

在理论上，RBF神经网络和BP神经网络一样能以任意精度逼近任何非线性函数[12]。但是因为它们各自的激励函数不同，其逼近能力也不同。BP神经网络是一种全局逼近型神经网络，其激励函数为Sigmoid函数。BP神经网络每次样本的学习都需要重新调整整个网络的权值，这样会导致训练速度很慢，并且容易容易陷入局部极小，因此难以满足控制系统高实时性要求。而RBF神经网络是一种局部逼近型神经网络，其激励函数为高斯函数，其在隐含层上实现对目标的局部逼近，在输出层上实现对目标的全局逼近，解决了BP 网络易陷入局部极小的问题，并且RBF神经网络还具有训练速度快，学习泛化能力较强的优点，其相较于BP神经网络有较快的收敛性，故采用RBF神经网络而不是BP神经网络去替代传统ip-iq法中的低通滤波器。

Matlab软件中的神经网络工具箱为用户提供了一个快速运用神经网络的GUI工具，使用这个工具可以对RBF神经网络进行建立、初始化、训练和仿真等各种操作，方面快捷。可以采用前述低通滤波器的输入输出数据作为RBF神经网络的训练数据，取稳定部分的数据，设定的仿真时间为1.0s，在此取0.6s-1.0s之间的稳定数据，一共4000组。建立好RBF神经网络后，利用gensim()函数对其生成相应的Simulink模块，如图3所示。

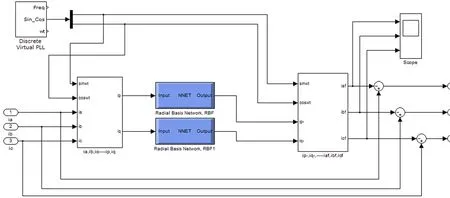
图3 采用RBF神经网络的仿真图

3 仿真验证及分析

采用Matlab/Simulink分别对传统的基于瞬时无功功率理论的ip-iq法和所提的改进进行仿真验证，电路图如图4所示。电路采用的电源为380V、50HZ的对称三相交流电压，谐波源由全控桥式整流电路，6路脉冲发生器及阻感性负载组成，仿真时间设置为1s。

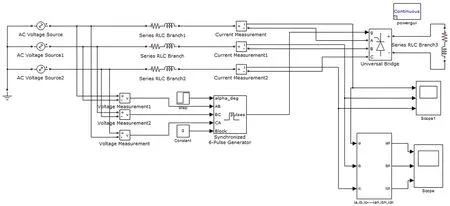
图4 谐波检测电路

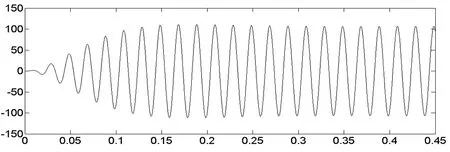
图5 使用LPF所测A相的基波电流

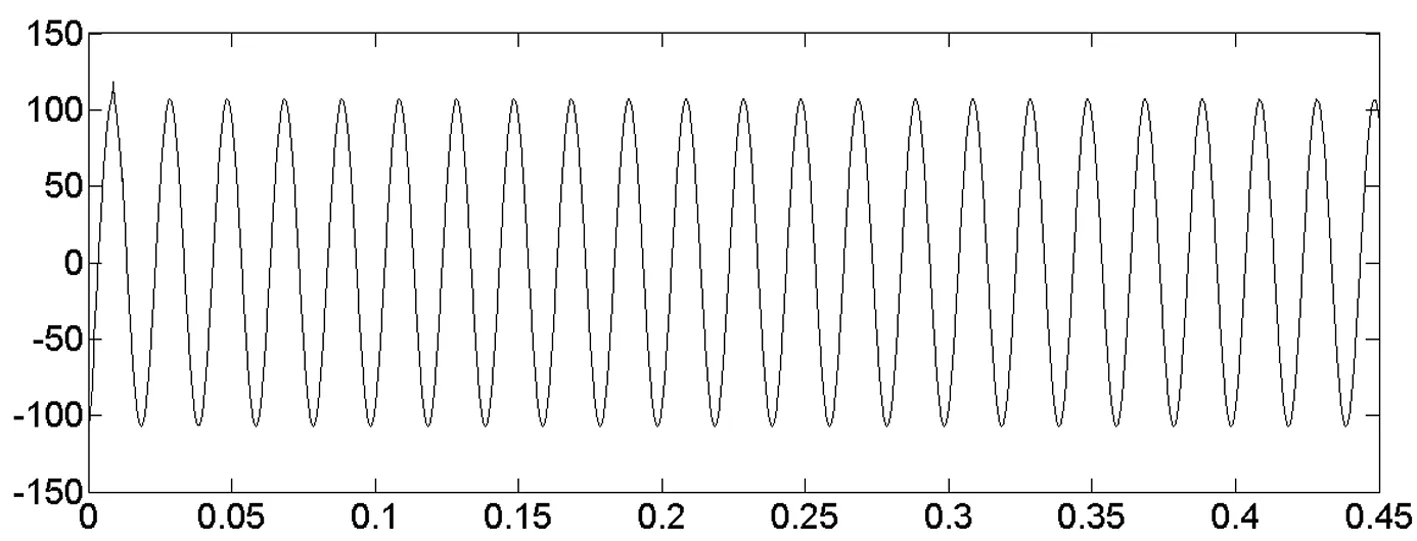
图6 使用RBFNN所测A相的基波电流

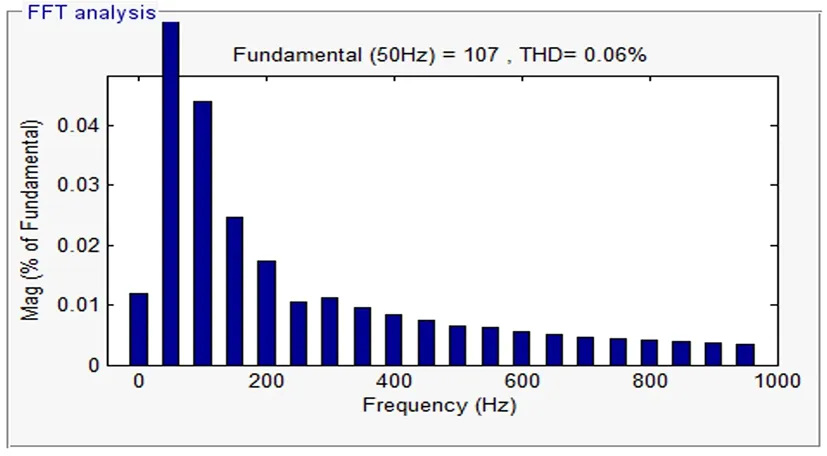
图7 LPF所测A相基波电流的FFT分析

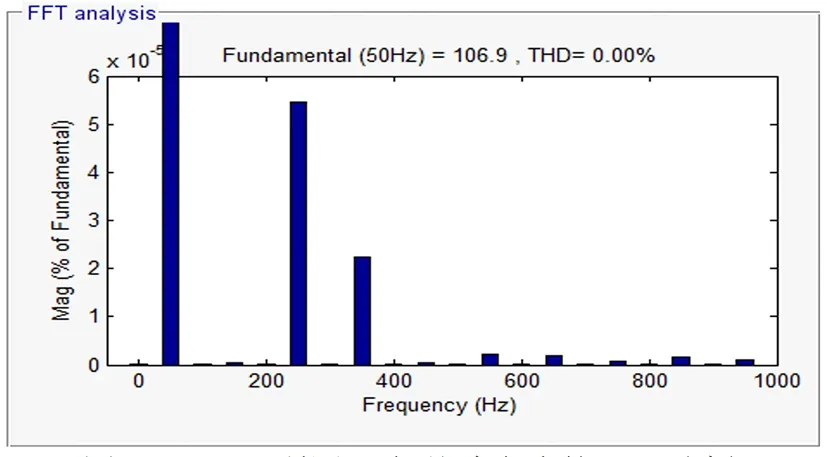
图8 RBFNN所测A相基波电流的FFT分析

经仿真得到以下实验图像，图5和图6分别是两种方法所测A相的基波电流波形， 图7和图8分别是对两种方法所测基波进行FFT分析得到的结果。

图5和图6说明传统ip-iq算法中低通滤波器所测到A相的基波电流约需要0.16s才能趋于稳定，这里低通滤波器的设置参数为2阶，25Hz的截止频率。而采用RBF神经网络来代替低通滤波器，可以发现延迟几乎为0，从一开始波形就很稳定，对比分析发现所提的改性在跟踪速度上相较于传统ip-iq算法有明显的优越性。

图7和图8说明传统ip-iq算法中所测A相基波电流THD=0.06%，而利用RBF神经网络所测A相基波电流THD=0.00%，两者测量的开始时间都为0.3s，对比分析发现所提的改进比传统ip-iq算法具有更高的检测精度。

4 结 论

为了突破基于传统瞬时无功功率理论ip-iq算法中的低通滤波器性能制约，提出用RBF神经网络来替代其实现滤波的改进，解决了低通滤波器对于谐波检测的跟踪速度和稳态精度之间的矛盾。仿真实验图像和数据表明，用RBF神经网络得到的基波相较于传统ip-iq法会更早达到稳定，延时大大缩短，并且由FFT分析基波发现，RBF神经网络得到的基波在同等条件下，THD较传统ip-iq法更小，检测结果精度更高，故所提的一种对于传统ip-iq法的改进是有可行性与可靠性的。