社会稳定风险定量分析方法新探讨—— 基于蒙特卡罗模拟的社会稳定风险定量分析

文/赵心田 刘俊颖 杨宣华

1.社会稳定风险的描述

风险是未来损失的不确定性[1]。在社会稳定风险中，“损失”则定义为发生群体性事件或个体极端事件，其程度则根据参与人数、冲突程度等来评价并量化为0～1不同的值；“不确定性”则表示为发生的概率以及影响的程度是不同的。对于社会风险的描述，可类似于：“该项目以40%概率造成0.5的社会稳定影响，以10%的概率造成0.8的影响。”

2.社会稳定风险分析定量分析现状

“综合风险指数法”是目前社会稳定风险定量分析中比较常见的方法。其思路为：先估计单因素的风险概率和影响程度，二者乘积为该因素的风险程度，再确定单因素风险在项目整体中的权重，然后对各因素的风险程度加权求和，作为整个项目的综合风险指数。“综合风险指数法”主要有两个缺点[2][3][4]：（1）无论是单因素风险还是项目整体风险，都是估计的具体值，并没有体现风险“不确定性”的特点；（2）加权会“稀释”某些重要风险在整体项目风险中的作用，可能导致因整体风险偏低而忽视某些个别的重要风险。针对第2点，徐成彬、李开孟、彭振武在文章[3]中提出了以问题解决为导向的社会稳定风险评估框架，以“发现问题-分析问题-解决问题”为主线，对单个风险因素进行风险程度的定性和定量评估，并提出风险防范和化解措施，使每一个风险因素都达到低风险并可控的状态。该方法强调了以解决风险问题为主，避免了加权带来的“稀释”作用。但该方法偏重定性分析，定量分析稍显不足。针对第1点，胡建一在文章[4]中，将项目的整体风险用概率的视角来对待，得出项目整体风险发生的可能性与可能发生的损失结果，这更符合风险的“不确定性”。但该方法中，对单个风险因素的估计，依然使用“点乘”的估计思路，没有体现出单因素风险的“不确定性”。

3.社会稳定风险定量分析方法新探讨

本文提出的定量分析思路旨在解决“综合指数法”的两个不足。本文将单个风险因素和项目整体风险都视为服从一定概率分布的随机变量，同时，对于单因素风险和项目整体风险关系，不使用“加权平均”的思路，而是构造一个新的风险决策函数。本文首先采用“三点估算法”对单因素风险进行估计，然后根据已定义的风险决策函数，利用蒙特卡罗模拟法对项目整体的风险进行定量分析。

3.1 单因素风险程度的估计

本研究将单个因素的风险影响程度视为服从一定概率分布的随机变量，例如图1所示，该风险40%概率造成0.4的影响程度，10%的概率造成0.7的影响程度。从这个角度出发，假如一个因素以较高概率发生较大影响，那就是个高风险因素，如果一个因素以较高概率产生较小的影响，那就是个低风险因素。

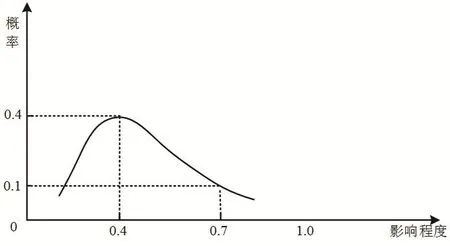
图1 单因素风险影响程度概率分布图

图2 贝塔分布图

基于此，对单因素风险进行定量估计，就变成估计该风险因素影响程度的概率密度函数。然而，鉴于社会稳定风险定量分析的相关研究起步较晚，可参考的历史数据少，前期调研也更多的是定性资料，导致对于概率分布的假设和参数估计几乎是没有数据来支撑的。针对该类情况，本文借鉴项目风险决策中较为成熟的一种方法—三点估算法，对单因素风险进行参数估计。

（1）三点估算法

三点估算法最初是来自于计划评审技术（Program Evaluation and Review Technique，简称 PERT），PERT是目前工程实践中运用非常广泛的一种工程项目进度风险分析方法[7]。PERT 于1958年由美国海军武器规划局的工程技术人员提出，他们运用该方法决策北极星导弹潜艇的建造，提前两年完成任务，取得巨大的成功。经典的PERT方法认为，项目的各项活动花费的时间是一个随机变量（设为X），不能估计出其准确值，但假设X服从贝塔分布，可以用三个值对该分布进行刻画估计：最乐观时间a、最悲观时间b、最可能的时间m（如图2）。

在前期量化资料很少的情况下，将风险的影响程度假设为贝塔分布是一种经验性的做法，从项目风险管理的运用来看，这种假设是合理的[8]。本文设单因素风险为变量X，并假设其服从贝塔分布，利用a,b,m便可以估算出X的均值（u表示，下同）与方差（σ2表示，下同），分别如公式（1）和（2）所示：

关于上述式子的估算，文献[5]第二章节中提到了华罗庚教授对其做过的通俗解释。

利用三点估算（a,m,b）以及公式（1）（2），便可以完成贝塔分布的未知参数的估计。(a,m,b)由评估专家依据前期的调研资料和经验进行估算，其中：

•最乐观的估计：事情进展比较顺利，考虑到的困难点几乎没有出现，这种情况得到估计值a。

•最可能的估计：根据历史经验，借鉴同类项目的情况，判断考虑到的困难点最可能影响的程度，在这种情况下得到估计值m。

•最悲观的估计：事情进展不是很顺利，许多潜在的困难点都出现了，甚至还有没有考虑到的困难出现，在这种情况下得到估计值b。

（2）贝塔分布的参数估计

单因素风险X服从贝塔分布 ，贝塔分布总共有4个参数，其中a,b决定了分布的区间，r,s决定了分布的形状。其均值与方差分别如公式(3)和(4)所示：

该分布中，概率最大的数为众数m（即最可能的估值），根据贝塔分布的公式，利用导数df(x) /d/d(x)=0即得

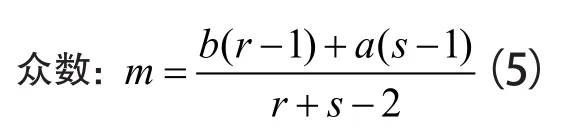
利用公式（3）（4）（5）中任意两个带入（1）（2）可得r和s的估计。注意这里的r，s可能并非唯一解，需保证r>0，s>0。比如这里用（3）（5）带入（1）（2）即得：

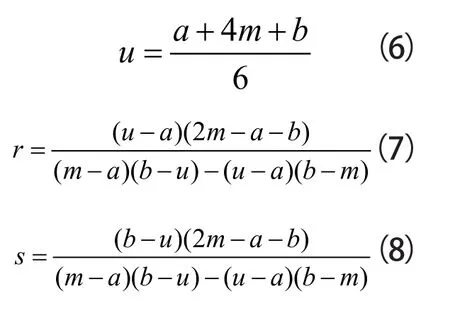
利用a,b,m便完成了贝塔分布4个参数（a,b,r,s）的估计。

3.2风险决策函数：风险因素和项目整体风险的关系

设X1,X2,⋅⋅⋅,Xn为n个单 因素风险随机变量，项目整体风险为Y，风险决策函数为Y=F(X1,X2,⋅⋅,Xn)。“综合风险指数法”中该决策函数相当于Y=WiXi，其中Xi为第i个风险因素的风险程度，Wi为第i个风险因素的权重。但该公式是欠妥的[2]，尤其是权重会导致项目整体风险被拉低。若一个项目具有某项可能引发社会稳定的风险，如征地补偿可能引发群体性事件，则该风险就是项目整体风险，不存在局部风险和整体风险区分的问题[2]。比如有3个风险因素，风险程度等级分别为较大、一般、较小，则项目整体风险程度不应该低于较大风险的等级程度。受该思路的启发，本文提出的风险决策函数如公式（9）所示：

该函数表示用风险因素中风险程度最大的定义为项目整体风险程度。该决策函数有如下好处：

•避免了加权平均可能会导致的“稀释”作用。

•整体风险程度不低于任意一个风险因素的风险程度，这也符合实际的情况。

•如果想让项目整体风险降低，则需要重点关注影响程度最大的风险因素，将其影响程度降低。这点和中国国际工程咨询有限公司提出的“以问题解决为导向”的评价框架[3]中“以项目的所有社会稳定风险均处于‘低风险且可控’状态为评判准则”是相吻合的。

•单因素风险程度是随机变量，由该决策函数计算所得的项目整体风险程度依然是一个随机变量，也具有“不确定性”的特点。

3.3蒙特卡罗模拟

项目社会稳定风险分析和评估有两个重要目标：第一，确定项目的整体风险程度，为决策者提供依据；第二，识别出项目中最主要的几个风险因素，重点分析并提出全面的风险防范和化解措施。基于上述（3.1）（3.2）的单因素风险假设和决策函数，可以通过蒙特卡罗模拟对上述两个目标进行定量的分析。

（1）蒙特卡罗模拟流程及原理

蒙特卡罗模拟方法是一种以数理统计理论为基础的仿真方法，广泛运用于风险决策的量化分析中。其基本原理：设是n个风险因素的随机变量，这n个随机变量的概率分布是已知的，风险决策函数为这个函数表达式也是已知的。蒙特卡罗模拟方法依据随机变量各自的概率分布随机生成一组确定的值将这组值带入决策函数，求得y的值这就完成一次模拟的过程。蒙特卡罗模拟往往是要进行成千上万次，得到一系列的y值然后通过统计这一系列y的特征，完成对项目风险的量化分析。模拟次数越多，对y刻画的精确度越高。

社会稳定风险进行量化分析的蒙特卡罗模拟流程如图3所示：

① 识别风险因素，并确定各单因素风险的概率分布。这里各风险因素均假设为贝塔分布。

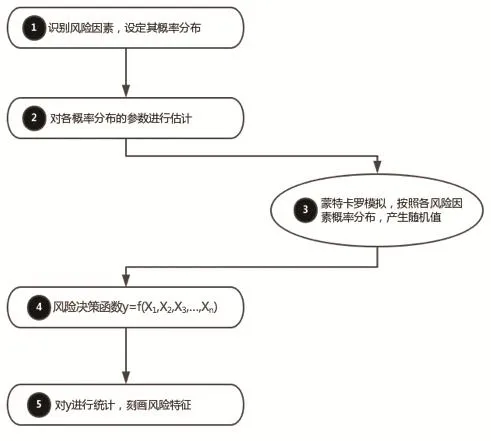
图3 蒙特卡罗模拟流程图

② 在①假设的概率分布基础上，对概率分布的参数进行估计。这里用三点估算法估计贝塔分布的各参数。

③在②的基础上利用蒙特卡罗模拟产生一组随机值。

④将③产生的值带入决策函数，并重复多次该过程，计算出一系列的y。

⑤对④所获得的一系列y值进行统计，从而刻画出项目的风险特征。

（2）确定项目整体风险程度

本文以风险程度高于0.64为高风险，0.36-0.64为中风险，0.36以下为低风险作为判定准则。假设随机模拟了N次获得了项目整体风险程度的N个值 ，则项目整体风险程度期望值如公式（10）所示：

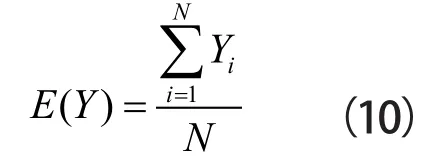
项目高风险、中风险与低风险的发生的概率为：

最后，本文以项目高、中、低风险的概率和整体风险程度期望值来定量刻画项目的整体风险。

（3）确定重点风险因素

对于单因素风险的重要程度，可以用以下的指标进行衡量：

期望值。可以直接用三点估算法中的期望公式，计算出该风险因素的影响程度的期望值，用期望值进行比较。或者用蒙特卡罗模拟中，求出各个风险程度的平均值

CRI（等级相关）。计算单个风险因素（Xi）对项目整体风险程度（Y）的影响程度大小，影响越大，则该风险因素越重要。衡量该影响的指标设计可以有多种，参考Williams(1993)[6]在网络评审计划研究中提出的活动重要性指标（Cruciality Index，CRI），又叫等级相关。CRI是用Xi和Y的相关系数 corr（Xi，Y）来衡量该风险因素对Y的影响。

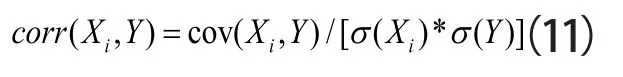
（4）工具推荐

蒙特卡罗模拟的工具很多，本文推荐一款excel的插件--Crystal Ball。Crystal Ball是美国Decisioneering公司开发的一款软件，是一款专门用来做风险评估和决策分析的工具。

4.案例分析

4.1 项目概述

该项目是某地区示范小城镇农民安置用房项目，通过前期的风险尽职调查和专家的讨论，共识别出8项风险因素，并利用“综合指数法”进行量化评估，结果如表1所示。

用综合风险指数的方法评估后，措施前项目整体风险等级为中风险，措施后为低风险。

4.2 蒙特卡罗模拟方法进行风险分析

（1）单因素风险的估计

根据调研资料和经验专家对每个风险因素分别估计出最乐观值、最可能值和最悲观值等三个值，然后对各个专家的估计值进行平均，获得每个风险因素的三点估计值（见表2）。例如，措施前“规划和审批”和“征地拆迁补偿”两个风险因素，在综合指数法中，二者的风险程度得分较为接近，均为较大风险。由于项目的前期很多审批程序都还在进行中，因此专家在打分上面对“规划和审批”的风险影响打分都比较高，最后该风险定为较大风险。但在三点估算法中，可以看到二者的明显区别：最乐观估计中，对于“规划和审批”假如前置审批顺利，其风险影响基本可以忽略，分值为0.1，但是对于“征地拆迁补偿”假如顺利的话，依然存在一些潜在的困难，不可将其忽视，分值为0.22。对于悲观的估计，即便“规划和审批”中出现了很多困难，但是对于社会稳定的影响还是有限的，分值0.4，但是“征地拆迁补偿”不一样，悲观的情况就是会引起群体事件，分值0.78。可以看到二者的概率密度如图4所示（其中“规划和审批”的概率密度如图4（1）所示，“征地拆迁补偿”如图4（2）所示），二者有明显的区别。因此，三点估算法可以反映比“综合指数法”更多的信息。

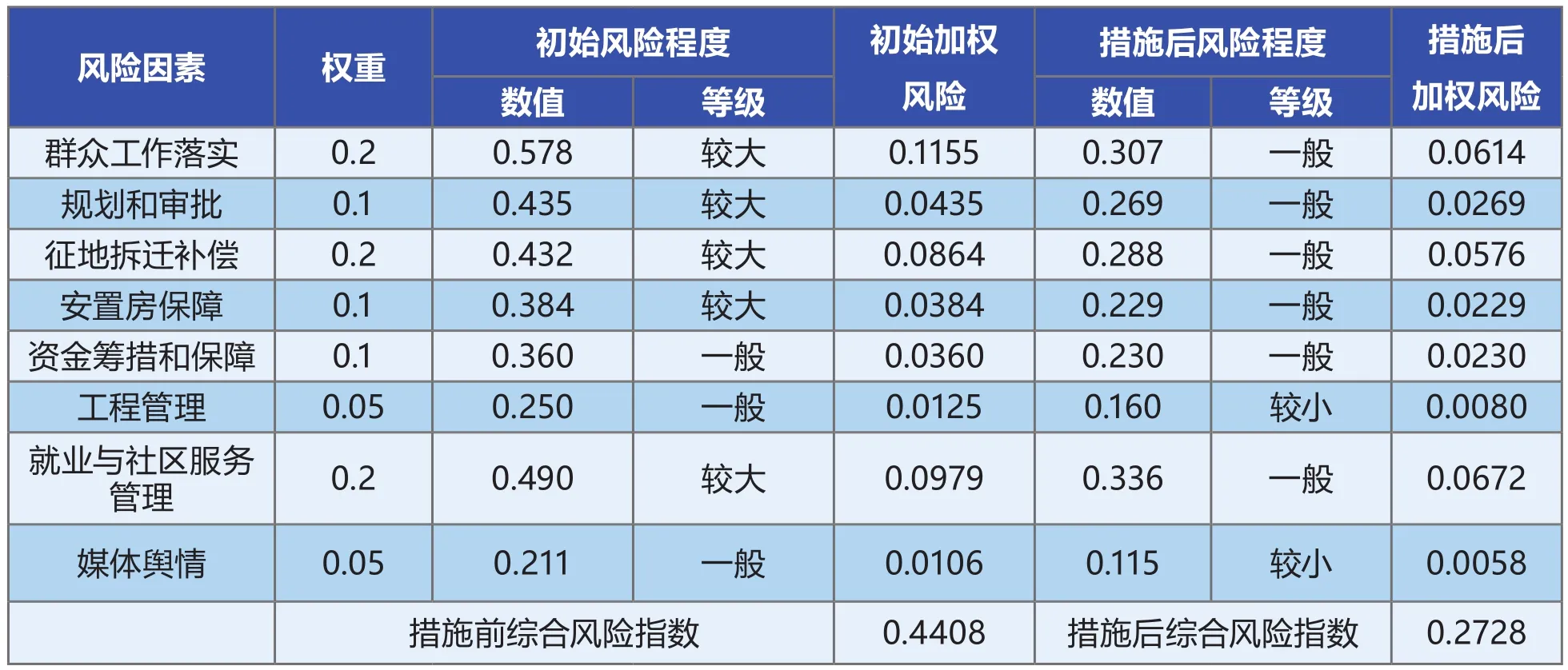
表1 应用“综合指数法”的风险量化评估结果

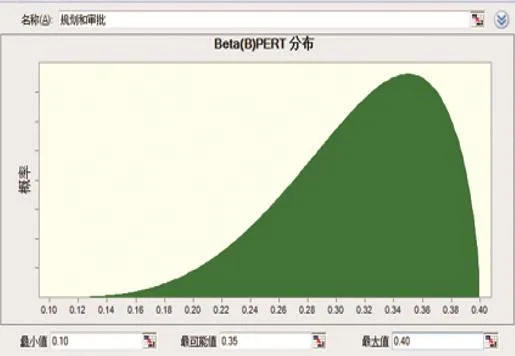
图4 （1）“规划和审批”风险的概率密度

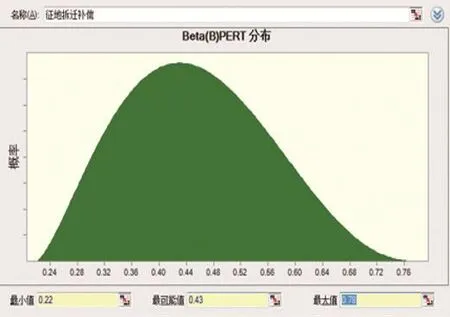
图4 （2）“征地拆迁补偿”风险的概率密度

落实措施后，再分别评估各风险因素最可能值、最乐观值，最悲观值。最后得到该项目各风险因素措施前后的三点估算值，如表2所示：

（2）蒙特卡罗模拟分析

项目的决策函数y=max（X1，X2，・・・，X8），设置模拟的次数为10000次，然后得到统计结果，并对项目整体风险和单因素风险分别进行量化分析。

1）措施前项目的整体风险

措施前的风险量化结果如图5所示，其中，项目的期望风险值为：0.55，其中，86%的概率是中风险，14%的概率是高风险，几乎不会出现低风险。

2）识别重要的风险因素

利用上文提到的CR（I等级相关）指标来评估各风险因素的重要程度。Crystal Ball中的敏感度分析部分，点击预测—>打开敏感度图，系统默认为方差贡献，此处本研究选择等级相关，其结果如图6所示，“群众工作落实”、“征地拆迁补偿”、“安置房保障”依次是和项目整体风险最相关的指标，应当重点关注，提出有效可行的风险防范和化解措施。

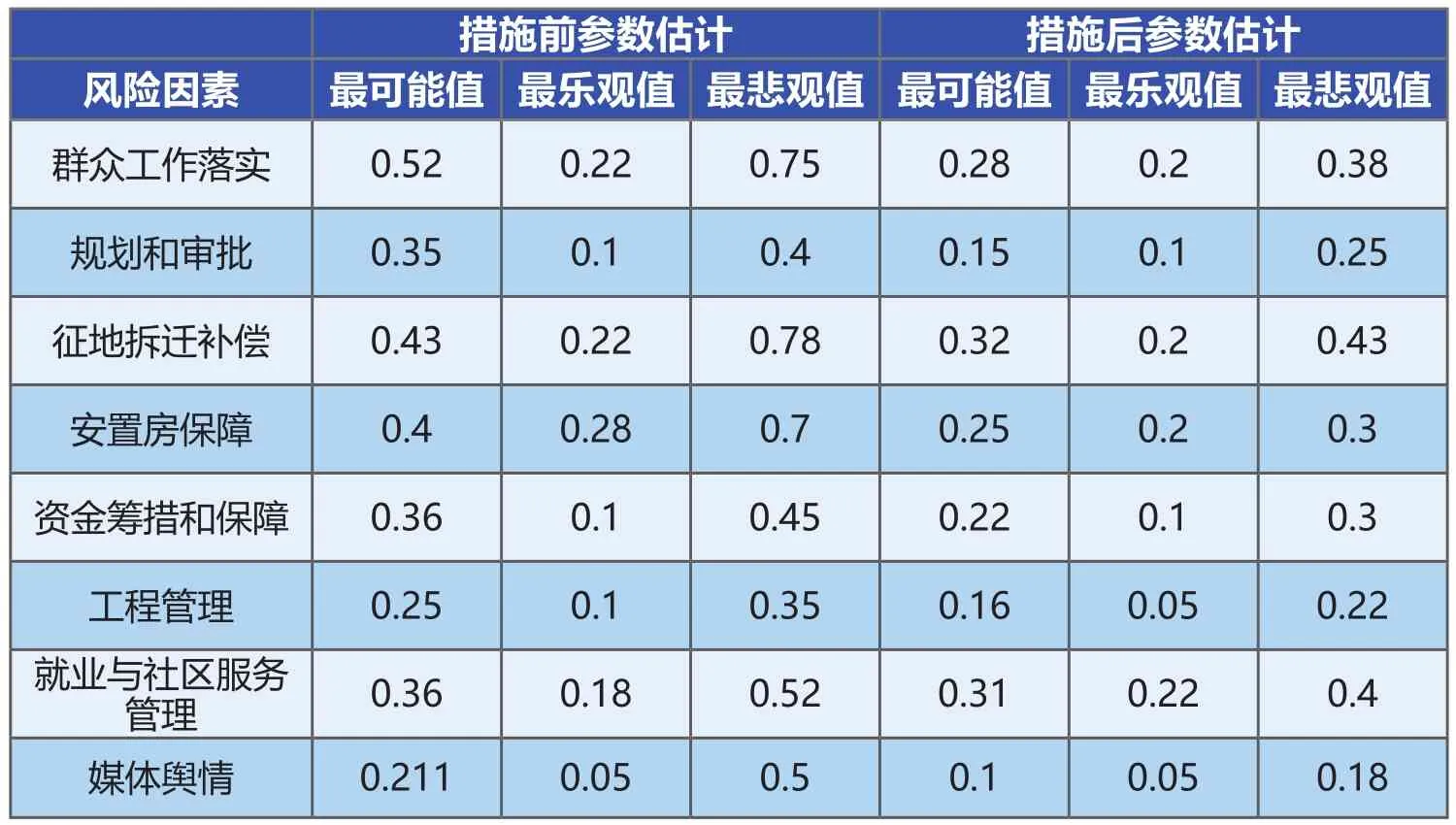
表2 项目各风险因素的三点估算值

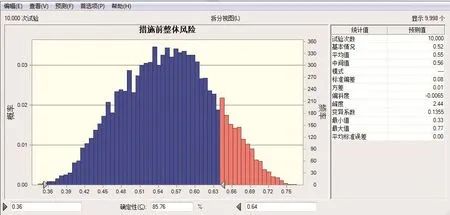
图5 措施前项目整体风险量化图

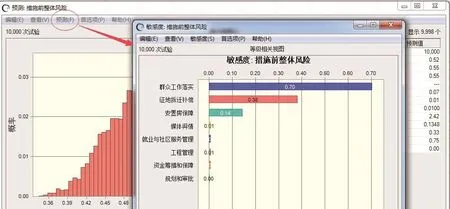
图6 CRI 敏感度图分析

3）措施后的项目整体风险

措施后，蒙特卡罗模拟结果图7所示：项目整体风险期望值为0.34，74%的概率是低风险，26%的概率中风险。

结果显示，该方法措施前后项目整体风险的期望值都高于综合指数法，因为该方法用最高的风险因素衡量项目整体风险，所以期望值会比用综合指数法的方法高。同时该方法还给出了项目处于各风险等级的概率，辅助风险决策。由于三点估算法，加入了更多差异的信息，这使得识别重点风险因素也更准确，如果想要降低项目的整体风险，那就需要将所有的风险因素都降低到可控的状态。

5.总结

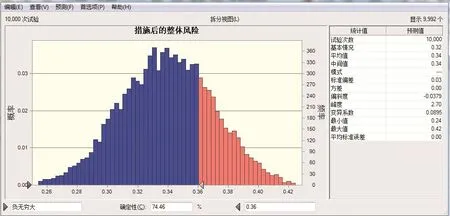
图7 措施后项目整体风险量化图

本文回顾和分析目前社会稳定风险定量分析的方法以及存在的问题，在此基础上探讨新的定量分析方法。该方法假设单因素风险为服从贝塔分布的随机变量，并用三点估算法对其进行参数估计。对于项目整体风险和单因素风险因素的关系，本文则以单因素风险中的最大值作为项目的整体风险值，该公式表明要想降低项目风险则需要将每个因素的风险都降低。最后基于蒙特卡罗模拟方法，对项目整体风险进行量化估计，获得决策的结果。该方法运用在一个项目案例上，不仅能够获得该项目整体风险的期望值，还能够获得项目处于高中低各等级风险的概率值，同时利用CRI指标，能够识别出重要的风险因素，运用风险防范化解措施后，模拟结果表明虽然项目的整体风险期望处于低风险，但仍有26%的可能性发生中风险，这有助于对风险更全面的认识，从而为决策提供更全面地视角。卡罗法的工程项目工期风险分析[D],三峡大学,2012.