分数阶玻色-爱因斯坦凝聚态的数值方法
2018-12-26邵永运韩子健张荣培
邵永运, 韩子健, 张荣培, 王 语
(1. 沈阳师范大学 学科与科研工作处, 沈阳 110034; 2. 沈阳师范大学 数学与系统科学学院, 沈阳 110034)
0 引 言
超低温磁囚禁原子气体凝聚实验的成功实现,引起了原子物理学界的广泛关注。自1995年以来,有关玻色-爱因斯坦凝聚(BEC)的实验取得了飞跃性的进展,与此同时,关于BEC的理论和数值方法也取得巨大的进步,计算BEC的基态、第一激发态以及动力学特性是BEC研究的基本问题之一。经典的非线性薛定谔(NLS)方程,也被称为Gross-Pitaevskii方程(GPE),已广泛用于描述BECs的基态和动力学特性。
近年来,分数阶算子的引入引起了人们对分数阶薛定谔方程的关注[1],在分数阶微分算子的离散方面,许多学者提出了不同的有限差分方法。 Meerschaert和Tadjeran[2]提出了一阶带有偏移项的Grünwald算子;基于以前的工作,田等[3]发展了两类二阶加权偏移Grünwald-Letnikov (WSGD)算子; Ortigueira首先提出了分数阶中心差分格式; Duman[4]对其进行了分析,将其应用于分数阶扩散方程;郭等[5]证明了它全局光滑解具有唯一性; Simone Secchi[6]利用Nehari流行最小化方法建立了薛定谔方程的一类解,包括分数阶拉普拉斯算子;Xavier Antoine[7]对无限势阱中分数阶薛定谔方程的基态和第一激发态进行了数值研究,并分析求解了分数阶拉普拉斯算子的特征值和特征函数;唐等[8]利用高效的数值方法解决了旋转和带有非局部相互作用的分数阶薛定谔方程(FSE)中的基态和动力学问题。
本文针对分数阶玻色-爱因斯坦凝聚态(BEC)展开研究,当BEC中的粒子不服从高斯分布律时,分数阶薛定谔方程被命名为分数阶Gross-Pitaevskii方程(FGPC)[9-10]。本文将研究不同势阱中FGPE的基态和第一激发态,从而了解其数学和物理性质。在定态解中,应用离散化归一化梯度流(DNGF),用于证明其能量减少;在空间离散方面,使用具有二阶精度的WSGD方法;在时间离散方面,采用隐积分因子方法[11-12],该方法精度高、稳定性好。最后利用数值算例来验证理论分析。
1 分数阶Gross-Pitaevskii方程和归一化梯度流
1.1 分数阶Gross-Pitaevskii方程
通过在更一般的Lévy类量子路径上扩展Feynman路径积分方法,可以使用分数阶拉普拉斯算子-(-Δ)α替换经典的拉普拉斯算子Δ来获得分数阶Gross-Pitaevskii方程。
(1)
其中V(x)是一个实值的无量纲的势阱,其形状取决于系统的类型。本文采用的势阱为谐振子势[13]:
其中x∈R,γ是一个正常数。
一维情况下,式(1)中的分数阶拉普拉斯算子可以被定义为Riesz分数阶导数:
其中左右Riemann-Liouville分数阶导数定义如下:
(3)
式(2)中的Γ(·)表示标准的伽马函数。
在式(1)中有2个重要的不变量:
质量:
(4)
能量:
(5)
为了找到式(1)的稳定解,这个函数可以表示为
Ψ(x,t)=e-iμtφ(x)
(6)
其中:μ是凝聚物的化学势,φ是与时间无关的实函数。将式(6)带入式(1)中,得
在式(4)的条件下,
可以看到这个问题的本质是带约束条件的非线性特征值问题。相应的特征函数φ(x)可以通过使用下面的形式计算,特征值μ可以通过下式计算
这里Eβ(φ)是式(5)中给出的与φ相关的能量函数。在物理学的观点中,基态被认为是单位球面S={φ|‖φ‖=1,E(φ)<∞}上的能量最小值
其他能量大于Eg的特征函数在物理上称为激发态。
1.2 分数阶归一梯度流
使用归一化梯度流法来计算分数阶Gross-Pitaevskii方程的最小能量问题。将时间步长设为Δt,设Δt>0,显然,tn=nΔt,n=0,1,2,…,在每个时间间隔[tn,tn+1]内。对能量函数Eβ(ψ)采用最速下降法[14-15],可以得到
(7)
然后,在每个时间间隔结束时,通过投射单位球面式(4)来对该解进行归一化处理,即
(8)
从数值的角度来看,分数阶扩散方程可以用传统的有限差分方法进行离散化处理,并且可以在每个时间步长的末端实现归一化处理。离散归一化(GFDN)式(7)和式(8)的梯度流的初始条件可设为
φ(x,0)=φ0(x),x∈R, with‖φ0‖=1
2 数值方法
2.1 WSGD算子
到目前为止,Riemann-Liouville分数阶导数式(3)和Riesz分数导数式(2)可以通过多种差分方法近似,如WSGD方法[16-17]和分数阶中心差分方法[18]等,每种方法都有其自身的特点。本文将用WSGD方法近似左右Riemann-Liouville分数阶导数。偏移的Grünwald算子定义如下:


通过对偏移Gruünwald算子进行加权(WSGD),得
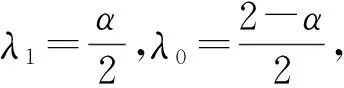
综上,WSGD算子可以重新定义为
并且,式(9)和式(10)中的系数满足以下条件
2.2 空间离散
在实际计算中,通常采用满足整个区间边界条件的有限子区间。 取Ω=[a,b],其中a和b足够大,以便忽略截断误差。
由于齐次Dirichlet边界条件,分数阶拉普拉斯算子可以表示为
空间区域Ω=[a,b]离散为
xj=a+jh,j=0,1,…,J
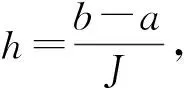
由此,得到了WSGD逼近算子
(11)
φ在节点xj处的解可以用一个列向量表示出来
Φ=(φ1φ2…φJ)T
分数阶微分算子的微分矩阵可以表示为
式(11)中分数阶拉普拉斯算子的微分矩阵可以定义为
综上,完成了关于空间的离散,得到了如下的常微分方程组:
(12)
2.3 隐式积分因子法
半离散公式(12)可以改写为以下形式:
(13)
其中:A=D;F(Φ)=-VΦ-β|Φ|2Φ;设时间步长为τ,则tn=nτ,n=0,1,2,…。
将式(13)左乘积分因子e-At并在一个时间步长tn到tn+1内进行积分,得
(14)
然后在tn+1,tn,…,tn-r+2点进行插值。通过r-1阶拉格朗日插值多项式来逼近式(14)中的被积函数以获得r阶的IIF格式,
在本文中,使用的是二阶的IIF格式(IIF2)如下:
3 数值实验

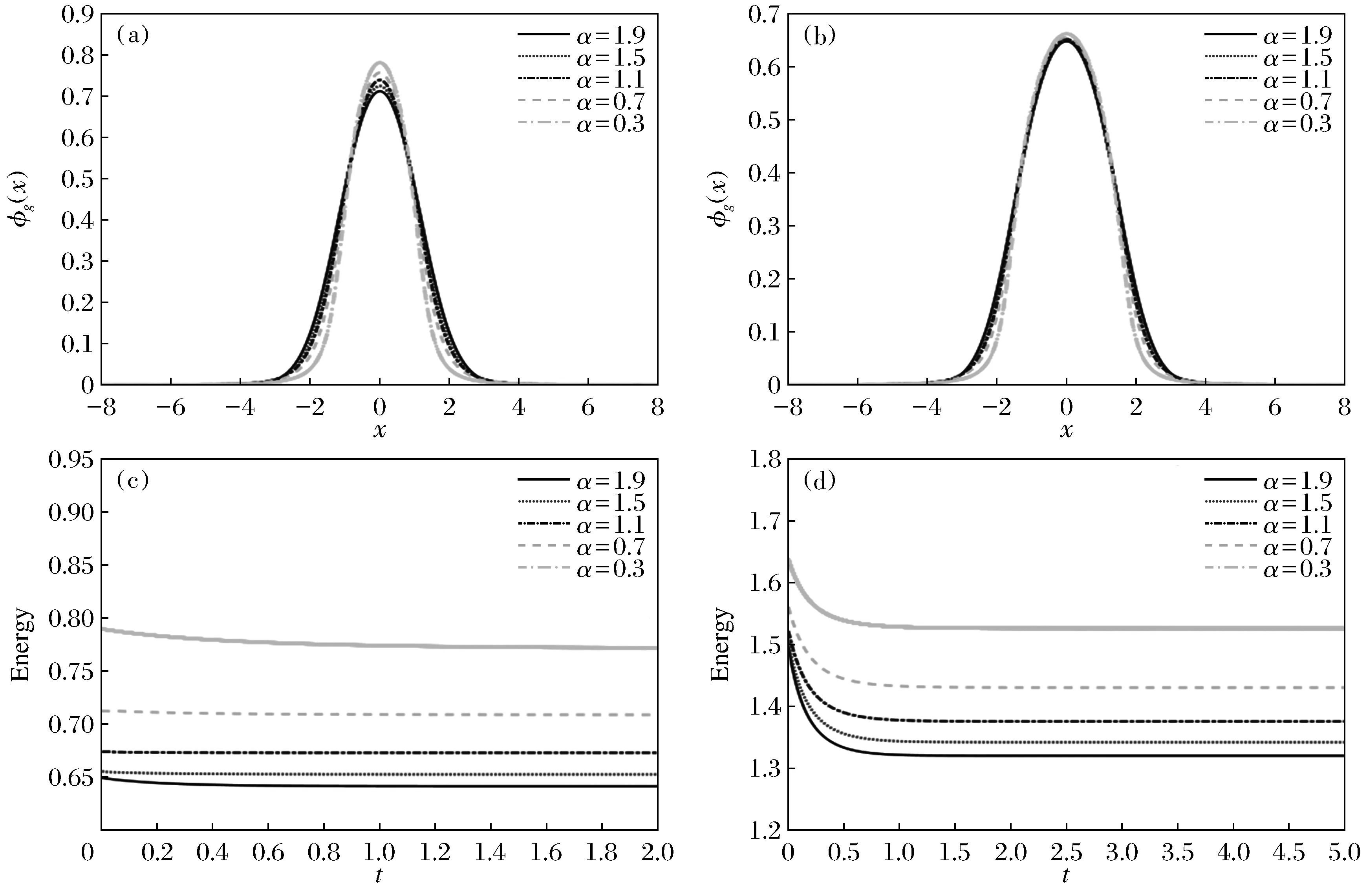
图1 (a) β=1和(b) β=3时的基态解及(c) β=1和(d) β=3时的能量演化


图2 (a) β=1和(b) β=5时的第一激发态解以及(c) β=1和(d) β=5时的能量演化
4 结 论
本文运用2种高效、高精度、高稳定性的数值计算方法计算分数阶非线性量子波动方程,即分数阶GP方程。WSGD方法有二阶精度,隐式积分因子法计算量和存储量小,并且2种方法均是无条件稳定的。通过与其他数值解法的比较,表明了这2种方法的可行性。数值实验计算了在区域边界和内部的并且带有谐振子势的基态和第一激发态。
